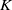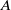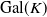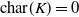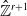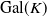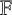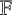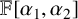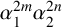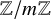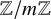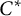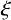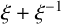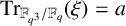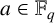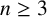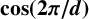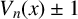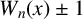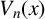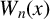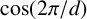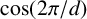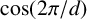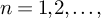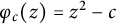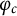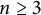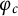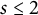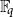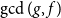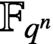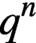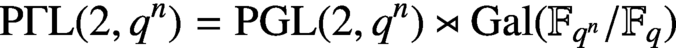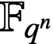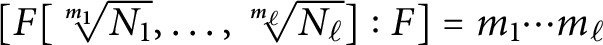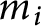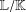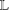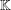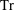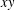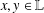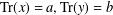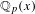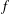51 results in 12Exx
Abelian absolute Galois groups: In Erinnerung an Wulf-Dieter Geyer (1939–2019)
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 02 February 2024, pp. 1-9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN ALGEBRAIC INTERPRETATION OF THE SUPER CATALAN NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 498-506
- Print publication:
- June 2024
-
- Article
- Export citation
Decidability of the class of all the rings
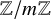 $\mathbb {Z}/m\mathbb {Z}$: A problem of Ax
$\mathbb {Z}/m\mathbb {Z}$: A problem of Ax
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 24 July 2023, e64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Noncommutative rational Clark measures
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 27 July 2022, pp. 1393-1445
- Print publication:
- October 2023
-
- Article
- Export citation
PRIMITIVE ELEMENT PAIRS WITH A PRESCRIBED TRACE IN THE CUBIC EXTENSION OF A FINITE FIELD
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 25 April 2022, pp. 458-462
- Print publication:
- December 2022
-
- Article
- Export citation
FACTORING VARIANTS OF CHEBYSHEV POLYNOMIALS WITH MINIMAL POLYNOMIALS OF
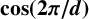 $\mathbf {cos}\boldsymbol {({2\pi }/{d})}$
$\mathbf {cos}\boldsymbol {({2\pi }/{d})}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 21 March 2022, pp. 448-457
- Print publication:
- December 2022
-
- Article
- Export citation
AN EFFECTIVE ANALYTIC FORMULA FOR THE NUMBER OF DISTINCT IRREDUCIBLE FACTORS OF A POLYNOMIAL
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 09 December 2021, pp. 339-356
- Print publication:
- December 2022
-
- Article
- Export citation
A NOTE ON GIRSTMAIR’S IRREDUCIBILITY CRITERION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 04 November 2021, pp. 62-66
- Print publication:
- August 2022
-
- Article
- Export citation
THE p-ZASSENHAUS FILTRATION OF A FREE PROFINITE GROUP AND SHUFFLE RELATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 29 September 2021, pp. 961-983
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some results on the Flynn–Poonen–Schaefer conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 11 August 2021, pp. 598-611
- Print publication:
- September 2022
-
- Article
- Export citation
Average-case complexity of the Euclidean algorithm with a fixed polynomial over a finite field
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 06 July 2021, pp. 166-183
-
- Article
- Export citation
GENERATORS OF FINITE FIELDS WITH PRESCRIBED TRACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 27 May 2021, pp. 355-366
- Print publication:
- June 2022
-
- Article
- Export citation
A CLASS OF FIELDS WITH A RESTRICTED MODEL COMPLETENESS PROPERTY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 26 March 2021, pp. 701-708
- Print publication:
- June 2021
-
- Article
- Export citation
MÖBIUS–FROBENIUS MAPS ON IRREDUCIBLE POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 14 December 2020, pp. 66-77
- Print publication:
- August 2021
-
- Article
- Export citation
On the degree of repeated radical extensions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 23 November 2020, pp. 877-885
- Print publication:
- December 2021
-
- Article
- Export citation
ON THE PRODUCT OF ELEMENTS WITH PRESCRIBED TRACE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 14 May 2020, pp. 264-288
- Print publication:
- April 2022
-
- Article
- Export citation
PRIMITIVE RECURSIVE DECIDABILITY FOR THE RING OF INTEGERS OF THE COMPOSITUM OF ALL SYMMETRIC EXTENSIONS OF ℚ
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 08 May 2020, pp. 291-296
- Print publication:
- May 2021
-
- Article
- Export citation
WILD RAMIFICATION IN TRINOMIAL EXTENSIONS AND GALOIS GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 12 March 2020, pp. 106-120
- Print publication:
- January 2021
-
- Article
- Export citation
LARGE FIELDS IN DIFFERENTIAL GALOIS THEORY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 27 January 2020, pp. 1931-1946
- Print publication:
- November 2021
-
- Article
- Export citation
A NEW PROOF OF THE CARLITZ–LUTZ THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 10 July 2019, pp. 56-60
- Print publication:
- February 2020
-
- Article
- Export citation