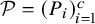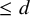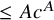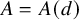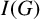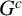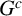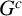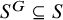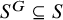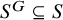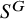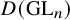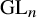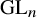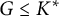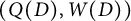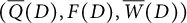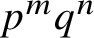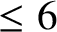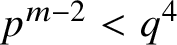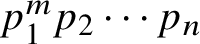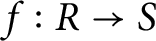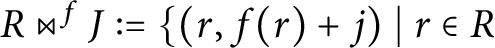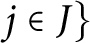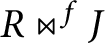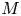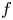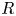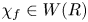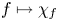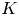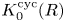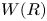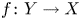89 results in 13Fxx
Relative rank and regularization
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 06 March 2024, e29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HOMOLOGICAL LINEAR QUOTIENTS AND EDGE IDEALS OF GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 29 January 2024, pp. 1-12
-
- Article
- Export citation
DILOGARITHM IDENTITIES IN CLUSTER SCATTERING DIAGRAMS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 21 December 2023, pp. 1-22
- Print publication:
- March 2024
-
- Article
- Export citation
When are the natural embeddings of classical invariant rings pure?
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 03 August 2023, e67
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multiple generalized cluster structures on
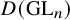 $D(\mathrm {GL}_n)$
$D(\mathrm {GL}_n)$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 09 June 2023, e46
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Product decompositions of moment-angle manifolds and B-rigidity
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1313-1325
- Print publication:
- December 2023
-
- Article
- Export citation
A CATEGORIFICATION OF ACYCLIC PRINCIPAL COEFFICIENT CLUSTER ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 252 / December 2023
- Published online by Cambridge University Press:
- 22 February 2023, pp. 769-809
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mutation-finite quivers with real weights
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 10 February 2023, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
D-finite multivariate series with arithmetic restrictions on their coefficients
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 03 October 2022, pp. 1745-1779
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bökstedt periodicity and quotients of DVRs
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 27 September 2022, pp. 1683-1712
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Calabi–Yau properties of Postnikov diagrams
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 21 July 2022, e56
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Classification of singularities of cluster algebras of finite type: the case of trivial coefficients
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 04 July 2022, pp. 170-204
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quivers with potentials for Grassmannian cluster algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 21 June 2022, pp. 1199-1225
- Print publication:
- August 2023
-
- Article
- Export citation
On the structure of spectral and tiling subsets of cyclic groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 May 2022, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Casting light on shadow Somos sequences
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue S1 / May 2023
- Published online by Cambridge University Press:
- 10 May 2022, pp. S87-S101
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hilbert rings with maximal ideals of different heights and unruly Hilbert rings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 10 March 2022, pp. 196-203
- Print publication:
- March 2023
-
- Article
- Export citation
Embedding codimension of the space of arcs
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 21 February 2022, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONTINUOUS QUIVERS OF TYPE A (III) EMBEDDINGS OF CLUSTER THEORIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 247 / September 2022
- Published online by Cambridge University Press:
- 11 February 2022, pp. 653-689
- Print publication:
- September 2022
-
- Article
- Export citation
Witt vectors with coefficients and characteristic polynomials over non-commutative rings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 26 April 2022, pp. 366-408
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A uniform treatment of Grothendieck's localization problem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 57-88
- Print publication:
- January 2022
-
- Article
- Export citation