Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-01-15T13:51:10.921Z Has data issue: false hasContentIssue false
  • English
  • Français

Quivers with potentials for Grassmannian cluster algebras

Part of: Arithmetic rings and other special rings Representation theory of rings and algebras

Published online by Cambridge University Press:  21 June 2022

Wen Chang Open the ORCID record for Wen Chang [Opens in a new window]  and
Jie Zhang
Wen Chang
Affiliation:
School of Mathematics and Information Science, Shaanxi Normal University, Xi’an 710062, China e-mail: changwen161@163.com
Jie Zhang*
Affiliation:
School of Mathematics and Statistics, Beijing Institute of Technology, 100081 Beijing, P. R. China
*
e-mail: jiezhang@bit.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a quiver with potential (QP) 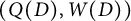$(Q(D),W(D))$ and an iced quiver with potential (IQP) 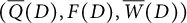$(\overline {Q}(D), F(D), \overline {W}(D))$ associated with a Postnikov Diagram D and prove that their mutations are compatible with the geometric exchanges of D. This ensures that we may define a QP 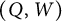$(Q,W)$ and an IQP 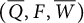$(\overline {Q},F,\overline {W})$ for a Grassmannian cluster algebra up to mutation equivalence. It shows that 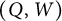$(Q,W)$ is always rigid (thus nondegenerate) and Jacobi-finite. Moreover, in fact, we show that it is the unique nondegenerate (thus rigid) QP by using a general result of Geiß, Labardini-Fragoso, and Schröer (2016, Advances in Mathematics 290, 364–452).

Then we show that, within the mutation class of the QP for a Grassmannian cluster algebra, the quivers determine the potentials up to right equivalence. As an application, we verify that the auto-equivalence group of the generalized cluster category 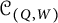${\mathcal {C}}_{(Q, W)}$ is isomorphic to the cluster automorphism group of the associated Grassmannian cluster algebra 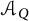${{\mathcal {A}}_Q}$ with trivial coefficients.

Keywords

Quiver with potentialGrassmannian cluster algebracluster category

MSC classification

Primary: 13F60: Cluster algebras
Secondary: 16G20: Representations of quivers and partially ordered sets
Type
Article
Information
Canadian Journal of Mathematics , Volume 75 , Issue 4 , August 2023 , pp. 1199 - 1225
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Wen Chang is supported by the NSF of China (Grant No. 11601295), Shaanxi Province, and Shaanxi Normal University. Jie Zhang is supported by the NSF of China (Grant Nos. 12071026 and 12122101), Beijing, and Beijing Institute of Technology.

References

Amiot, C., Cluster categories for algebras of global dimension 2 and quivers with potential . Ann. Inst. Fourier (Grenoble) 59(2009), no. 6, 2525–2590.10.5802/aif.2499CrossRefGoogle Scholar
Amiot, C., On generalized cluster categories . In: Representations of algebras and related topics, EMS Series of Congress Reports, European Mathematical Society, Zürich, 2011, pp. 1–53.Google Scholar
Amiot, C., Iyama, O., and Reiten, I., Stable categories of Cohen–Macaulay modules and cluster categories . Amer. J. Math. 137(2015), no. 3, 813–857.CrossRefGoogle Scholar
Amiot, C., Reiten, I., and Todorov, G., The ubiquity of generalized cluster categories . Adv. Math. 226(2011), no. 4, 3813–3849.10.1016/j.aim.2010.10.028CrossRefGoogle Scholar
Assem, I., Schiffler, R., and Shramchenko, V., Cluster automorphisms . Proc. Lond. Math. Soc. (3) 104(2012), no. 6, 1271–1302.CrossRefGoogle Scholar
Baur, K., King, A., and Marsh, R., Dimer models and cluster categories of Grassmannians . Proc. Lond. Math. Soc. (3) 113(2016), no. 2, 213–260.10.1112/plms/pdw029CrossRefGoogle Scholar
Berenstein, A., Fomin, S., and Zelevinsky, A., Cluster algebras. III. Upper bounds and double Bruhat cells . Duke Math. J. 126(2005), no. 1, 1–52.10.1215/S0012-7094-04-12611-9CrossRefGoogle Scholar
Broomhead, N., Dimer models and Calabi–Yau algebras . Mem. Amer. Math. Soc. 215(2012), no. 1011, viii+86 pp.Google Scholar
Buan, A. B., Iyama, O., Reiten, I., and Scott, J., Cluster structures for 2-Calabi–Yau categories and unipotent groups . Compos. Math. 145(2009), no. 4, 1035–1079.CrossRefGoogle Scholar
Buan, A. B., Iyama, O., Reiten, I., and Smith, D., Mutation of cluster-tilting objects and potentials . Amer. J. Math. 133(2011), no. 4, 835–887.CrossRefGoogle Scholar
Chang, W. and Zhu, B., Cluster automorphism groups of cluster algebras with coefficients . Sci. China Math. 59(2016), no. 10, 1919–1936.CrossRefGoogle Scholar
Chang, W. and Zhu, B., Cluster automorphism groups of cluster algebras of finite type . J. Algebra 447(2016), 490–515.CrossRefGoogle Scholar
Derksen, H., Weyman, J., and Zelevinsky, A., Quivers with potentials and their representations I: mutations . Selecta Math. 14(2008), no. 1, 59–119.CrossRefGoogle Scholar
Fomin, S. and Zelevinsky, A., Cluster algebras. I. Foundations . J. Amer. Math. Soc. 15(2002), no. 2, 497–529.CrossRefGoogle Scholar
Fomin, S. and Zelevinsky, A., Cluster algebras. II. Finite type classification . Invent. Math. 154(2003), no. 1, 63–121.CrossRefGoogle Scholar
Fomin, S. and Zelevinsky, A., Cluster algebras IV: coefficients . Compos. Math. 143(2007), 112–164.10.1112/S0010437X06002521CrossRefGoogle Scholar
Fu, C. and Keller, B., On cluster algebras with coefficients and 2-Calabi–Yau categories . Trans. Amer. Math. Soc. 362(2010), no. 2, 859–895.CrossRefGoogle Scholar
Geiß, C., Labardini-Fragoso, D., and Schröer, J., The representation type of Jacobian algebras . Adv. Math. 290(2016), 364–452.CrossRefGoogle Scholar
Geiß, C., Leclerc, B., and Schröer, J., Partial flag varieties and preprojective algebras . Ann. Inst. Fourier (Grenoble) 58(2008), 825–876.CrossRefGoogle Scholar
Geuenich, J., Labardini-Fragoso, D., and Miranda-Olvera, J. L., Quivers with potentials associated to triangulations of closed surfaces with at most two punctures. Preprint, 2020. arXiv:2008.10168 Google Scholar
Jensen, B., King, A., and Su, X., A categorification of Grassmannian cluster algebras . Proc. Lond. Math. Soc. (3) 113(2016), no. 2, 185–212.CrossRefGoogle Scholar
Keller, B. and Reiten, I., Acyclic Calabi–Yau categories . Compos. Math. 144(2008), no. 5, 1332–1348. With an appendix by Michel Van den Bergh.CrossRefGoogle Scholar
Keller, B. and Yang, D., Derived equivalences from mutations of quivers with potential . Adv. Math. 226(2011), no. 3, 2118–2168.CrossRefGoogle Scholar
Kulkarni, M., Dimer models on cylinders over Dynkin diagrams and cluster algebras . Proc. Amer. Math. Soc. 147(2019), no. 3, 921–932.CrossRefGoogle Scholar
Labardini-Fragoso, D., Quivers with potentials associated to triangulated surfaces . Proc. Lond. Math. Soc. (3) 98(2009), no. 3, 797–839.CrossRefGoogle Scholar
Labardini-Fragoso, D., Quivers with potentials associated to triangulated surfaces, part IV: removing boundary assumptions . Selecta Math. (N.S.) 22(2016), no. 1, 145–189.CrossRefGoogle Scholar
Leclerc, B., Cluster structures on strata of flag varieties . Adv. Math. 300(2016), 190–228.CrossRefGoogle Scholar
Postnikov, A., Total positivity, Grassmannians, and networks. Preprint, 2006. arXiv:math/0609764v1 Google Scholar
Pressland, M., Mutation of frozen Jacobian algebras . J. Algebra 546(2020), 236–273.CrossRefGoogle Scholar
Scott, J., Grassmannians and cluster algebras . Proc. Lond. Math. Soc. (3) 92(2006), no. 2, 345–380.10.1112/S0024611505015571CrossRefGoogle Scholar
Vitória, J., Mutations vs. Seiberg duality . J. Algebra 321(2009), no. 3, 816–828.CrossRefGoogle Scholar
Yang, D., The interplay between 2-and-3-Calabi–Yau triangulated categories. Preprint, 2018. arXiv:1811.07553 Google Scholar