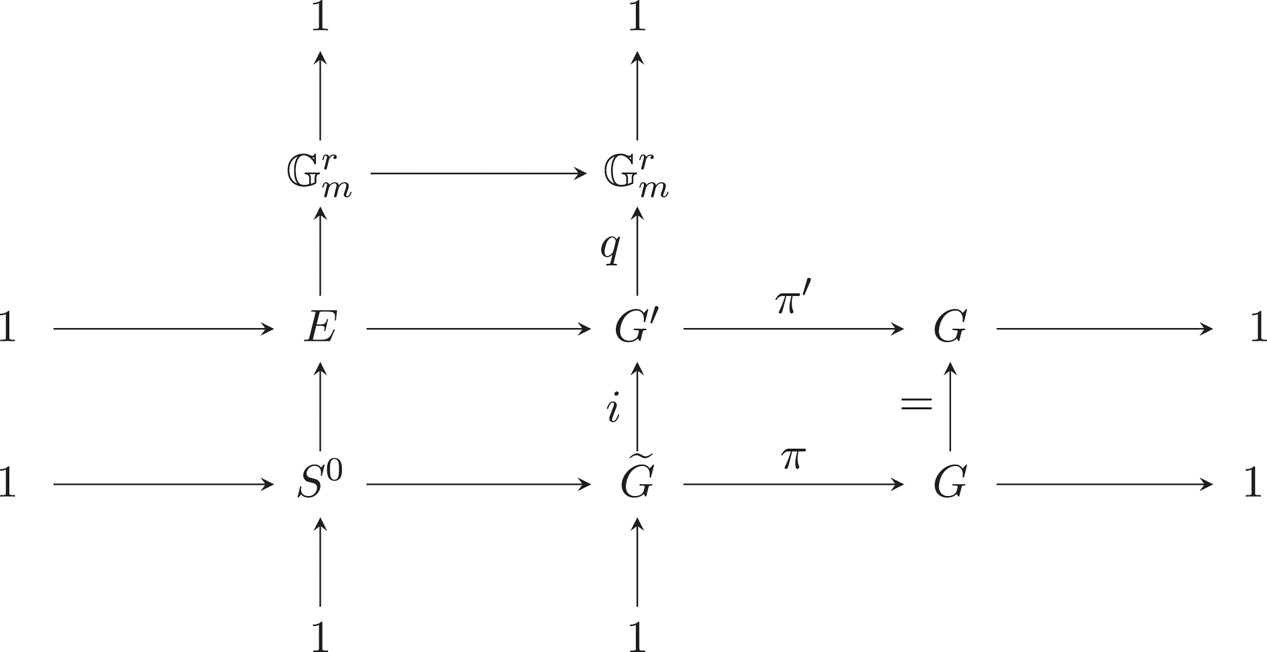
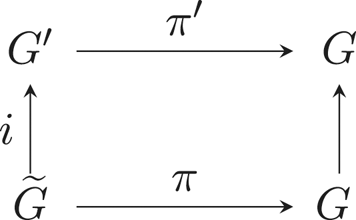
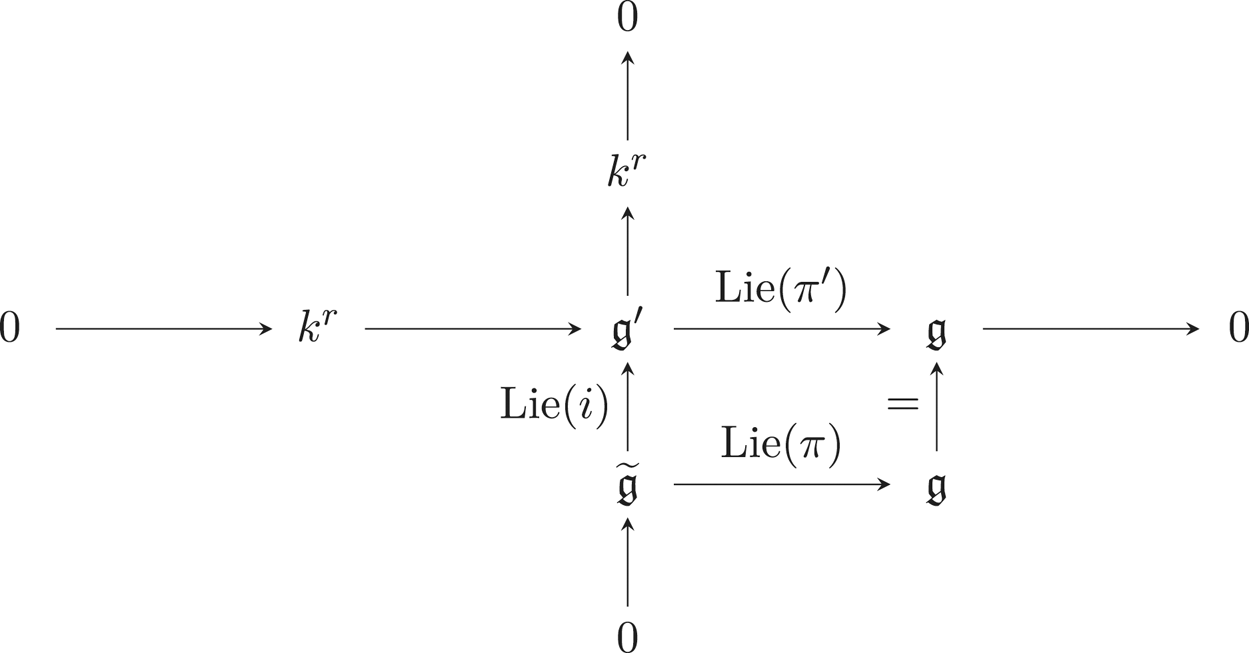
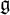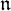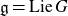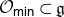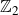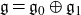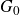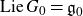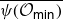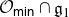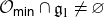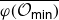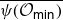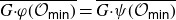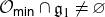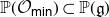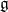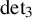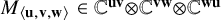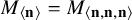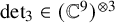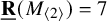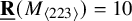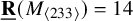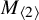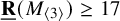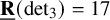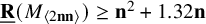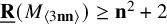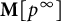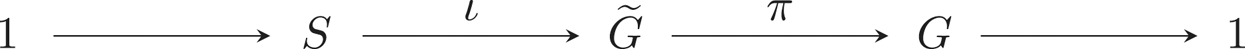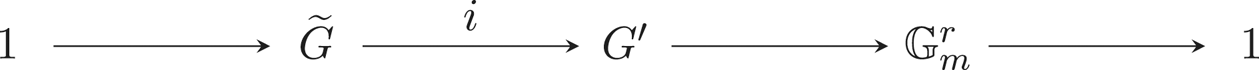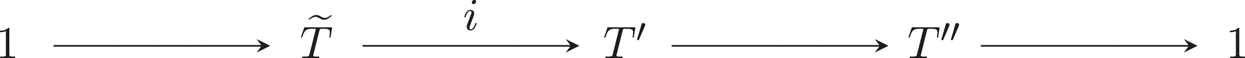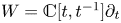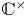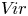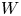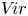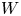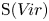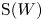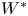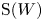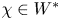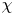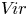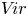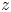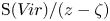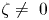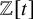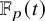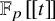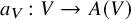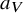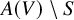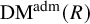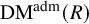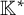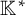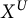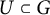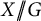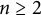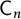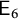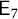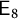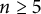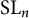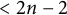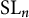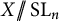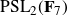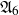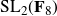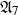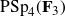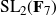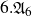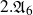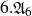135 results in 14Lxx
On irreducible representations of Fuchsian groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 27 August 2024, pp. 1-21
-
- Article
- Export citation
Affine Bruhat order and Demazure products
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 April 2024, e53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the moduli of hypersurfaces in toric orbifolds
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 14 March 2024, pp. 577-616
-
- Article
- Export citation
Lie algebra actions on module categories for truncated shifted yangians
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 31 January 2024, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Bezrukavnikov–Kaledin quantization of symplectic varieties in characteristic p
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 411-450
- Print publication:
- February 2024
-
- Article
- Export citation
The Grothendieck–Serre conjecture over valuation rings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 317-355
- Print publication:
- February 2024
-
- Article
- Export citation
Stability conditions for polarised varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 20 November 2023, e104
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Frobenius semiradical, generic stabilizers, and Poisson center for nilradicals
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 27 October 2023, pp. 1-30
-
- Article
- Export citation
NON-ISOMORPHIC SMOOTH COMPACTIFICATIONS OF THE MODULI SPACE OF CUBIC SURFACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 254 / June 2024
- Published online by Cambridge University Press:
- 03 October 2023, pp. 315-365
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Projections of the minimal nilpotent orbit in a simple Lie algebra and secant varieties
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 13 July 2023, pp. 595-624
- Print publication:
- November 2023
-
- Article
- Export citation
Generic differential equations are strongly minimal
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 08 June 2023, pp. 1387-1412
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
New lower bounds for matrix multiplication and
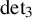 $\operatorname {det}_3$
$\operatorname {det}_3$
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 29 May 2023, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Log p-divisible groups associated with log 1-motives
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 28 April 2023, pp. 946-983
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integration questions in separably good characteristics
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 890-932
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Poisson spectrum of the symmetric algebra of the Virasoro algebra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 18 April 2023, pp. 933-984
- Print publication:
- May 2023
-
- Article
- Export citation
Grassmanniennes affines tordues sur les entiers
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 23 February 2023, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effective characterization of quasi-abelian surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 02 February 2023, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Prismatic Dieudonné Theory
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 06 January 2023, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Small G-varieties
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 04 January 2023, pp. 173-215
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite quasisimple groups acting on rationally connected threefolds
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 06 December 2022, pp. 531-568
- Print publication:
- May 2023
-
- Article
- Export citation









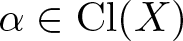



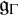


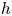
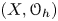
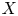
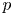
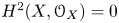
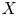
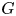
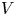
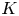
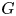
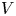
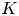
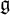
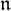
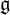

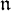
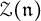 of the symmetric algebra
of the symmetric algebra 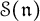 ,
, 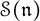 as
as 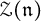 -module, and
-module, and