Let  $p(n)$ and
$p(n)$ and  $M(m,L;n)$ be the number of partitions of n and the number of partitions of n with crank congruent to m modulo L, respectively, and let
$M(m,L;n)$ be the number of partitions of n and the number of partitions of n with crank congruent to m modulo L, respectively, and let  $$ \begin{align*}M(a,b,c;L;n):= M(a,L;n) + M(b,L;n) + M(c,L;n).\end{align*} $$
$$ \begin{align*}M(a,b,c;L;n):= M(a,L;n) + M(b,L;n) + M(c,L;n).\end{align*} $$
In this paper, we focus on some relations between  $M(m,L;n)$ and
$M(m,L;n)$ and  $p(n),$ which Dyson, Andrews, and Garvan etc. have studied previously. By applying a modification of the circle method to estimate the Fourier coefficients of generating functions, we establish the following inequalities between
$p(n),$ which Dyson, Andrews, and Garvan etc. have studied previously. By applying a modification of the circle method to estimate the Fourier coefficients of generating functions, we establish the following inequalities between 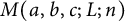 $M(a,b,c;L;n)$ and
$M(a,b,c;L;n)$ and 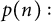 $p(n):$ for
$p(n):$ for  $n \geq 467$,
$n \geq 467$, 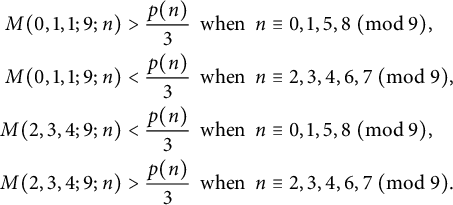 $$ \begin{align*} M(0,1,1;9;n)> \frac{p(n)}{3} &\;\: \mathrm{when}\;\: n \equiv 0,1,5,8 ~ (\mathrm{mod}~9), \\ M(0,1,1;9;n) < \frac{p(n)}{3} &\;\: \mathrm{when}\;\: n \equiv 2,3,4,6,7 ~ (\mathrm{mod}~9), \\ M(2,3,4;9;n) < \frac{p(n)}{3} &\;\: \mathrm{when}\;\: n \equiv 0,1,5,8 ~ (\mathrm{mod}~9), \\ M(2,3,4;9;n)> \frac{p(n)}{3} &\;\: \mathrm{when}\;\: n \equiv 2,3,4,6,7 ~ (\mathrm{mod}~9). \end{align*} $$
$$ \begin{align*} M(0,1,1;9;n)> \frac{p(n)}{3} &\;\: \mathrm{when}\;\: n \equiv 0,1,5,8 ~ (\mathrm{mod}~9), \\ M(0,1,1;9;n) < \frac{p(n)}{3} &\;\: \mathrm{when}\;\: n \equiv 2,3,4,6,7 ~ (\mathrm{mod}~9), \\ M(2,3,4;9;n) < \frac{p(n)}{3} &\;\: \mathrm{when}\;\: n \equiv 0,1,5,8 ~ (\mathrm{mod}~9), \\ M(2,3,4;9;n)> \frac{p(n)}{3} &\;\: \mathrm{when}\;\: n \equiv 2,3,4,6,7 ~ (\mathrm{mod}~9). \end{align*} $$
In the proof of these inequalities, an inequality for the logarithm of the generating function for  $p(n)$ is derived and applied. Our method reduces the last possible counterexamples to
$p(n)$ is derived and applied. Our method reduces the last possible counterexamples to  $467 \leq n \leq 22471$, and it will produce more effective estimates when proving inequalities of such types.
$467 \leq n \leq 22471$, and it will produce more effective estimates when proving inequalities of such types.
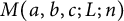 $M(a,b,c;L;n)$ and the partition function
$M(a,b,c;L;n)$ and the partition function  $p(n)$
$p(n)$
