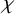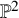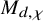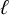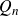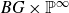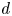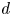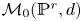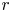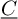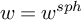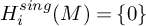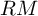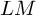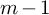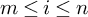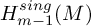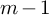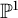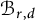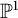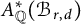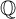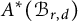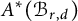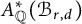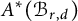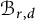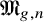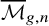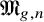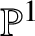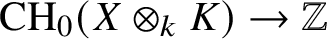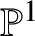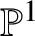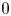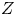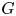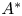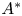47 results
Cohomological
 $\chi $-dependence of ring structure for the moduli of one-dimensional sheaves on
$\chi $-dependence of ring structure for the moduli of one-dimensional sheaves on 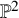 $\mathbb {P}^2$
$\mathbb {P}^2$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 01 April 2024, e47
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On Bloch’s map for torsion cycles over non-closed fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 22 June 2023, e53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integral Fourier transforms and the integral Hodge conjecture for one-cycles on abelian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1188-1213
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Coniveau filtrations and Milnor operation
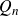 $Q_n$
$Q_n$
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 08 May 2023, pp. 521-538
- Print publication:
- November 2023
-
- Article
- Export citation
The integral Chow ring of
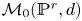 $\mathcal {M}_{0}(\mathbb {P}^r, d)$, for
$\mathcal {M}_{0}(\mathbb {P}^r, d)$, for 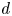 $d$ odd
$d$ odd
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 31 January 2023, pp. 184-206
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON MORPHISMS KILLING WEIGHTS AND STABLE HUREWICZ-TYPE THEOREMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 24 October 2022, pp. 521-556
- Print publication:
- March 2024
-
- Article
- Export citation
LAURICELLA HYPERGEOMETRIC FUNCTIONS, UNIPOTENT FUNDAMENTAL GROUPS OF THE PUNCTURED RIEMANN SPHERE, AND THEIR MOTIVIC COACTIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 249 / March 2023
- Published online by Cambridge University Press:
- 26 September 2022, pp. 148-220
- Print publication:
- March 2023
-
- Article
- Export citation
The six-functor formalism for rigid analytic motives
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 08 August 2022, e61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The intersection theory of the moduli stack of vector bundles on
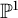 $\mathbb {P}^1$
$\mathbb {P}^1$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 07 July 2022, pp. 359-379
- Print publication:
- June 2023
-
- Article
- Export citation
Chow rings of stacks of prestable curves I
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 26 May 2022, e28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unramified logarithmic Hodge–Witt cohomology and
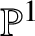 $\mathbb {P}^1$-invariance
$\mathbb {P}^1$-invariance
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 16 March 2022, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chow groups and L-derivatives of automorphic motives for unitary groups, II.
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 04 March 2022, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GYSIN TRIANGLES IN THE CATEGORY OF MOTIFS WITH MODULUS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 06 January 2022, pp. 2131-2154
- Print publication:
- September 2023
-
- Article
- Export citation
ON THE CHOW THEORY OF PROJECTIVIZATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 11 November 2021, pp. 1465-1508
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cohomological invariants of root stacks and admissible double coverings
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 02 November 2021, pp. 202-224
- Print publication:
- February 2023
-
- Article
- Export citation
Algebraic cycles and Lehn–Lehn–Sorger–van Straten eightfolds
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 04 October 2021, pp. 884-907
-
- Article
- Export citation
Algebraic cycles and intersections of three quadrics
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 2 / September 2022
- Published online by Cambridge University Press:
- 07 September 2021, pp. 349-367
- Print publication:
- September 2022
-
- Article
- Export citation
On the Chow ring of some special Calabi–Yau varieties
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 308-327
- Print publication:
- June 2022
-
- Article
- Export citation
Hopf-theoretic approach to motives of twisted flag varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 29 April 2021, pp. 963-996
- Print publication:
- May 2021
-
- Article
- Export citation
ON THE CHOW RING OF CERTAIN LEHN–LEHN–SORGER–VAN STRATEN EIGHTFOLDS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 22 March 2021, pp. 253-276
- Print publication:
- May 2022
-
- Article
- Export citation