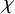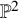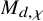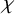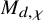1. Introduction
We work over the complex numbers
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
1.1. Moduli of sheaves
Fix two integers d and
![]() $\chi $
with
$\chi $
with
![]() $d\geq 1$
. We consider the moduli space
$d\geq 1$
. We consider the moduli space
![]() $M_{d,\chi }$
of semistable one-dimensional sheaves
$M_{d,\chi }$
of semistable one-dimensional sheaves
![]() $\mathcal {F}$
on
$\mathcal {F}$
on
![]() $\mathbb {P}^2$
with
$\mathbb {P}^2$
with
Here, H is the class of a line,
![]() $\mathrm {supp}(\mathcal {F})$
denotes the Fitting support and the stability condition is with respect to the slope
$\mathrm {supp}(\mathcal {F})$
denotes the Fitting support and the stability condition is with respect to the slope
Le Potier [Reference Le PotierLeP] first studied this moduli space and showed that
![]() $M_{d,\chi }$
is an irreducible projective variety of dimension
$M_{d,\chi }$
is an irreducible projective variety of dimension
![]() $d^2+1$
, nonsingular at all stable points. In particular, when d and
$d^2+1$
, nonsingular at all stable points. In particular, when d and
![]() $\chi $
are coprime, semistability coincides with stability and
$\chi $
are coprime, semistability coincides with stability and
![]() $M_{d,\chi }$
is nonsingular. Geometry and topology of the moduli space
$M_{d,\chi }$
is nonsingular. Geometry and topology of the moduli space
![]() $M_{d,\chi }$
have been intensively studied from various perspectives; see [Reference Pi and ShenPS, Introduction] for a brief overview. In this paper, we are interested in the cohomology rings
$M_{d,\chi }$
have been intensively studied from various perspectives; see [Reference Pi and ShenPS, Introduction] for a brief overview. In this paper, we are interested in the cohomology rings
![]() $H^*(M_{d,\chi }, \mathbb {C})$
for a fixed d and different Euler characteristics
$H^*(M_{d,\chi }, \mathbb {C})$
for a fixed d and different Euler characteristics
![]() $\chi $
coprime to d. Under the coprime assumption, the cycle class map
$\chi $
coprime to d. Under the coprime assumption, the cycle class map
is an isomorphism by [Reference MarkmanMar, Theorem 2]. Hence, in this case we use
![]() $A^*(-)$
to denote the even cohomology
$A^*(-)$
to denote the even cohomology
![]() $H^{2*}(-, \mathbb {C})$
, or equivalently the Chow ring
$H^{2*}(-, \mathbb {C})$
, or equivalently the Chow ring
![]() $\mathrm {CH}^*(-, \mathbb {C})$
with complex coefficients.
$\mathrm {CH}^*(-, \mathbb {C})$
with complex coefficients.
The moduli spaces
![]() $M_{d,\chi }$
admit two types of symmetries:
$M_{d,\chi }$
admit two types of symmetries:
-
(a) The first type of symmetry is given by the isomorphism
 $$\begin{align*}\psi_1 : M_{d,\chi} \xrightarrow{\sim} M_{d,\chi+d}, \;\; \mathcal{F} \mapsto \mathcal{F} \otimes \mathcal{O}_{\mathbb{P}^2}(1). \end{align*}$$
$$\begin{align*}\psi_1 : M_{d,\chi} \xrightarrow{\sim} M_{d,\chi+d}, \;\; \mathcal{F} \mapsto \mathcal{F} \otimes \mathcal{O}_{\mathbb{P}^2}(1). \end{align*}$$
-
(b) The second type of symmetry [Reference MaicanMai, Theorem 13] is given by the duality isomorphism
 $$\begin{align*}\psi_2 : M_{d,\chi} \xrightarrow{\sim} M_{d,-\chi}, \;\; \mathcal{F} \mapsto {\mathcal E} \kern -1.5 pt \mathit{xt}^1({\mathcal F}, \omega_{{\mathbb{P}}^2}). \end{align*}$$
$$\begin{align*}\psi_2 : M_{d,\chi} \xrightarrow{\sim} M_{d,-\chi}, \;\; \mathcal{F} \mapsto {\mathcal E} \kern -1.5 pt \mathit{xt}^1({\mathcal F}, \omega_{{\mathbb{P}}^2}). \end{align*}$$
Thus, given two Euler characteristics
![]() $\chi , \chi '$
satisfying
$\chi , \chi '$
satisfying
![]() $\chi \equiv \pm \chi '\ \mod d$
, there is a natural isomorphism
$\chi \equiv \pm \chi '\ \mod d$
, there is a natural isomorphism
![]() $M_{d,\chi } \simeq M_{d, \chi '}$
. The following theorem states that this is essentially the only case.
$M_{d,\chi } \simeq M_{d, \chi '}$
. The following theorem states that this is essentially the only case.
Theorem 1.1 [Reference WoolfWoo, Theorem 8.1].
For
![]() $d\geq 3$
, there is an isomorphism of algebraic varieties
$d\geq 3$
, there is an isomorphism of algebraic varieties
if and only if
![]() $\chi \equiv \pm \chi '\ \mod d$
.
$\chi \equiv \pm \chi '\ \mod d$
.
The main result of this paper is a cohomological version of Theorem 1.1:
Theorem 1.2. For
![]() $d\geq 1$
and
$d\geq 1$
and
![]() $\chi , \chi '$
coprime to d, there is an isomorphism of graded
$\chi , \chi '$
coprime to d, there is an isomorphism of graded
![]() $\mathbb {C}$
-algebras
$\mathbb {C}$
-algebras
if and only if
![]() $\chi \equiv \pm \chi '\ \mod d$
.
$\chi \equiv \pm \chi '\ \mod d$
.
We find this cohomological
![]() $\chi $
-dependence of ring structure interesting since the (intersection) Betti numbers of
$\chi $
-dependence of ring structure interesting since the (intersection) Betti numbers of
![]() $M_{d,\chi }$
are
$M_{d,\chi }$
are
![]() $\chi $
-independent: In particular, we have an isomorphism
$\chi $
-independent: In particular, we have an isomorphism
of graded vector spaces for arbitrary
![]() $\chi $
and
$\chi $
and
![]() $\chi '$
coprime to d; see Theorem 1.4 for the precise statement. As a corollary of Theorem 1.2, we deduce that
$\chi '$
coprime to d; see Theorem 1.4 for the precise statement. As a corollary of Theorem 1.2, we deduce that
![]() $M_{d,\chi }$
are in general topologically different, strengthening Theorem 1.1:
$M_{d,\chi }$
are in general topologically different, strengthening Theorem 1.1:
Corollary 1.3. For any
![]() $\chi , \chi '$
coprime to d, the moduli spaces
$\chi , \chi '$
coprime to d, the moduli spaces
![]() $M_{d,\chi }$
and
$M_{d,\chi }$
and
![]() $M_{d,\chi '}$
are not homeomorphic unless
$M_{d,\chi '}$
are not homeomorphic unless
![]() $\chi \equiv \pm \chi '\ \mod d$
.
$\chi \equiv \pm \chi '\ \mod d$
.
1.2. BPS invariants and
 $\chi $
-independence
$\chi $
-independence
One motivation to study the moduli spaces
![]() $M_{d,\chi }$
comes from enumerative geometry. Let
$M_{d,\chi }$
comes from enumerative geometry. Let
![]() $X= \mathrm {Tot}(K_{\mathbb {P}^2})$
be the local Calabi–Yau 3-fold given by the total space of the canonical bundle on
$X= \mathrm {Tot}(K_{\mathbb {P}^2})$
be the local Calabi–Yau 3-fold given by the total space of the canonical bundle on
![]() $\mathbb {P}^2$
. Considerations from physics [Reference Gopakumar and VafaGV] predict an action of the Lie algebra
$\mathbb {P}^2$
. Considerations from physics [Reference Gopakumar and VafaGV] predict an action of the Lie algebra
![]() $\mathfrak {sl}_2\times \mathfrak {sl}_2$
on the cohomology of a certain moduli space of D-branes supported on degree d curves in X, yielding double-indexed integral invariants
$\mathfrak {sl}_2\times \mathfrak {sl}_2$
on the cohomology of a certain moduli space of D-branes supported on degree d curves in X, yielding double-indexed integral invariants
as the dimensions of the weight spaces of this
![]() $\mathfrak {sl}_2\times \mathfrak {sl}_2$
-action. These are known as refined BPS invariants of X, named after Bogomol'nyi–Prasad–Sommerfield, which are expected to refine curve counting invariants for X defined via Gromov–Witten/Donaldson–Thomas/Pandharipande–Thomas theory [Reference Pandharipande and ThomasPT].
$\mathfrak {sl}_2\times \mathfrak {sl}_2$
-action. These are known as refined BPS invariants of X, named after Bogomol'nyi–Prasad–Sommerfield, which are expected to refine curve counting invariants for X defined via Gromov–Witten/Donaldson–Thomas/Pandharipande–Thomas theory [Reference Pandharipande and ThomasPT].
One proposal by Hosono–Saito–Takahashi [Reference Hosono, Saito and TakahashiHST], Kiem–Li [Reference Kiem and LiKL] and Maulik–Toda [Reference Maulik and TodaMT] suggests a mathematical definition of the invariants (1.1) by the perverse filtration on the cohomology of moduli spaces of one-dimensional sheaves. More precisely, the moduli space
![]() $M_{d,\chi }$
admits a Hilbert–Chow morphism
$M_{d,\chi }$
admits a Hilbert–Chow morphism
sending a sheaf to its Fitting support. This map is proper and induces an increasing filtration on the intersection cohomology
called the perverse filtration; see [Reference Kononov, Pi and ShenKPS, Section 1.1]. The invariants (1.1) are defined in loc. cit. as the dimension of the graded pieces of this filtration:
For this to be well defined, the right-hand side in Equation (1.2) should not depend on the choice of
![]() $\chi $
, which is a priori nontrivial in light of Theorem 1.1. This is a special case of Toda’s cohomological
$\chi $
, which is a priori nontrivial in light of Theorem 1.1. This is a special case of Toda’s cohomological
![]() $\chi $
-independence conjecture [Reference TodaTod, Conjecture 1.2]; see also [Reference BousseauBou, Conjecture 0.4.3] for a version on the intersection Betti numbers of
$\chi $
-independence conjecture [Reference TodaTod, Conjecture 1.2]; see also [Reference BousseauBou, Conjecture 0.4.3] for a version on the intersection Betti numbers of
![]() $M_{d,\chi }$
. The following theorem of Maulik and Shen confirms this conjecture.Footnote
1
$M_{d,\chi }$
. The following theorem of Maulik and Shen confirms this conjecture.Footnote
1
Theorem 1.4 [Reference Maulik and ShenMS1, Theorem 0.1].
For any
![]() $\chi , \chi ' \in \mathbb {Z}$
not necessarily coprime to d, there is a (noncanonical) isomorphism of graded vector spaces
$\chi , \chi ' \in \mathbb {Z}$
not necessarily coprime to d, there is a (noncanonical) isomorphism of graded vector spaces
preserving the perverse filtration on both sides.
If we restrict to the coprime case, intersection cohomology coincides with singular cohomology which admits a canonical
![]() $\mathbb {Q}$
-algebra structure. It is then natural to ask if we can choose the isomorphism of Theorem 1.4 to be an isomorphism of
$\mathbb {Q}$
-algebra structure. It is then natural to ask if we can choose the isomorphism of Theorem 1.4 to be an isomorphism of
![]() $\mathbb {Q}$
-algebras. More generally, we can ask the following:
$\mathbb {Q}$
-algebras. More generally, we can ask the following:
Question 1.5 [Reference Pi and ShenPS, Section 0.3].
For any
![]() $\chi , \chi '$
coprime to d, is there an isomorphism
$\chi , \chi '$
coprime to d, is there an isomorphism
of graded
![]() $\mathbb {Q}$
-algebras?
$\mathbb {Q}$
-algebras?
Theorem 1.2 gives a complete answer to this question in the stronger sense that we work with
![]() $\mathbb {C}$
-coefficients instead of
$\mathbb {C}$
-coefficients instead of
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
1.3. Structure of the proof of Theorem 1.2
We outline the proof of our main result here, as the argument is of an elementary nature but somewhat long. It was explained in [Reference Pi and ShenPS] that the rings
![]() $A^\ast (M_{d,\chi })$
admit a minimal set of
$A^\ast (M_{d,\chi })$
admit a minimal set of
![]() $3d-7$
generators
$3d-7$
generators
 $$\begin{align*}T=\{c_0(2), c_2(0)\}\cup \bigcup_{k=2}^{d-2}\{c_{k-1}(2), c_k(1), c_{k+1}(0)\}\,.\end{align*}$$
$$\begin{align*}T=\{c_0(2), c_2(0)\}\cup \bigcup_{k=2}^{d-2}\{c_{k-1}(2), c_k(1), c_{k+1}(0)\}\,.\end{align*}$$
In other words, there is a surjective graded algebra homomorphism
![]() ${\mathbb {C}}[T]\twoheadrightarrow A^\ast (M_{d,\chi })$
. This homomorphism is an isomorphism up to degree
${\mathbb {C}}[T]\twoheadrightarrow A^\ast (M_{d,\chi })$
. This homomorphism is an isomorphism up to degree
![]() $d-1$
, but in degree d there are exactly there relations, cf. Theorem 2.2. As a first step toward the proof, we show that these three relations
$d-1$
, but in degree d there are exactly there relations, cf. Theorem 2.2. As a first step toward the proof, we show that these three relations
![]() $R_1, R_2, R_3$
spanning
$R_1, R_2, R_3$
spanning
![]() $\ker ({\mathbb {C}}[T]^d\to A^d(M_{d,\chi }))$
can be obtained explicitly from the tautological relations of [Reference Pi and ShenPS, Section 2], cf. Proposition 2.7.
$\ker ({\mathbb {C}}[T]^d\to A^d(M_{d,\chi }))$
can be obtained explicitly from the tautological relations of [Reference Pi and ShenPS, Section 2], cf. Proposition 2.7.
We then proceed by showing that if
![]() $\chi $
and
$\chi $
and
![]() $\chi '$
are not related by the symmetries (a) and (b), that is,
$\chi '$
are not related by the symmetries (a) and (b), that is,
![]() $\chi \not \equiv \pm \chi '\ \mod d$
, then there is no automorphism of the graded algebra
$\chi \not \equiv \pm \chi '\ \mod d$
, then there is no automorphism of the graded algebra
![]() ${\mathbb {C}}[T]$
that sends the three-dimensional subspace of relations
${\mathbb {C}}[T]$
that sends the three-dimensional subspace of relations
![]() $\ker ({\mathbb {C}}[T]^d\to A^d(M_{d,\chi }))\subseteq {\mathbb {C}}[T]^d$
to
$\ker ({\mathbb {C}}[T]^d\to A^d(M_{d,\chi }))\subseteq {\mathbb {C}}[T]^d$
to
![]() $\ker ({\mathbb {C}}[T]^d\to A^d(M_{d,\chi '}))$
. To achieve this, we do not use the full relations
$\ker ({\mathbb {C}}[T]^d\to A^d(M_{d,\chi '}))$
. To achieve this, we do not use the full relations
![]() $R_1, R_2, R_3$
, whose sizes grow considerably as d increases but only a truncated version of those. Concretely, we project the subspaces of relations onto the 18-dimensional subspace
$R_1, R_2, R_3$
, whose sizes grow considerably as d increases but only a truncated version of those. Concretely, we project the subspaces of relations onto the 18-dimensional subspace
This truncated form of the relations is completely explicit: For each of the three relations, we only need to compute the 18 coefficients that are rational functions in d and
![]() $\chi $
.
$\chi $
.
Showing that there is no automorphism of
![]() ${\mathbb {C}}[T]$
relating the (truncated) subspaces of relations for
${\mathbb {C}}[T]$
relating the (truncated) subspaces of relations for
![]() $\chi $
and
$\chi $
and
![]() $\chi '$
then becomes a very concrete, but still involved, linear algebra problem. For this, we employ a determinant trick in Step 2 of Section 3 that imposes strong restrictions on the possible automorphisms. The latter fall into two types, which we call Type I and Type II solutions. We treat them separately in Sections 3.1–3.3, showing that both cannot exist by analyzing certain numerical constraints (see, for example, Equation (3.7)) on the triple
$\chi '$
then becomes a very concrete, but still involved, linear algebra problem. For this, we employ a determinant trick in Step 2 of Section 3 that imposes strong restrictions on the possible automorphisms. The latter fall into two types, which we call Type I and Type II solutions. We treat them separately in Sections 3.1–3.3, showing that both cannot exist by analyzing certain numerical constraints (see, for example, Equation (3.7)) on the triple
![]() $(d,\chi , \chi ')$
.
$(d,\chi , \chi ')$
.
Our proof of Theorem 1.2 involves heavy computations aided by the software Mathematica [M]. The code (together with a printed file) has been uploaded to the third author’s website https://github.com/Weite-Pi/weitepi.github.io under the name cohomological ring chi-dependence, which we shall frequently refer to in the later part of this paper.
1.4. Relations to other works
The moduli space
![]() $M_{d,\chi }$
shares similar features with two types of other moduli spaces, the moduli of Higgs bundlesFootnote
2
and the moduli of one-dimensional sheaves on K3 surfaces. The parallel of Question 1.5 for those cases has a positive answer. Cohomology rings of the moduli of Higgs bundles are proven to be
$M_{d,\chi }$
shares similar features with two types of other moduli spaces, the moduli of Higgs bundlesFootnote
2
and the moduli of one-dimensional sheaves on K3 surfaces. The parallel of Question 1.5 for those cases has a positive answer. Cohomology rings of the moduli of Higgs bundles are proven to be
![]() $\chi $
-independent in the stronger sense that perverse filtrations are preserved, as predicted by the
$\chi $
-independent in the stronger sense that perverse filtrations are preserved, as predicted by the
![]() $P=W$
conjecture [Reference de Cataldo, Hausel and MigliorinidCHM, Reference Maulik and ShenMS2, Reference Hausel, Mellit, Minets and SchiffmannHMMS]. A direct proof using techniques in characteristic p is given in [Reference de Cataldo, Maulik, Shen and ZhangdCMSZ]. The case of K3 surfaces follows from the fact that moduli of sheaves on K3 surfaces with respect to a primitive class and generic stability is birational to the Hilbert scheme of points [Reference Bayer and MacrìBM] and that any two birational projective hyperkähler manifolds are deformation equivalent [Reference HuybrechtsHuy].
$P=W$
conjecture [Reference de Cataldo, Hausel and MigliorinidCHM, Reference Maulik and ShenMS2, Reference Hausel, Mellit, Minets and SchiffmannHMMS]. A direct proof using techniques in characteristic p is given in [Reference de Cataldo, Maulik, Shen and ZhangdCMSZ]. The case of K3 surfaces follows from the fact that moduli of sheaves on K3 surfaces with respect to a primitive class and generic stability is birational to the Hilbert scheme of points [Reference Bayer and MacrìBM] and that any two birational projective hyperkähler manifolds are deformation equivalent [Reference HuybrechtsHuy].
Our main result asserts that the cohomology rings
![]() $H^{*}(M_{d,\chi }, \mathbb {C})$
are
$H^{*}(M_{d,\chi }, \mathbb {C})$
are
![]() $\chi $
-dependent in general; on the other hand, some
$\chi $
-dependent in general; on the other hand, some
![]() $\chi $
-independent multiplicative structures have been observed or speculated:
$\chi $
-independent multiplicative structures have been observed or speculated:
-
○ It is conjectured and proven under certain assumptions in [Reference Bojko, Lim and MoreiraBLM] that the Virasoro constraints hold for the moduli spaces
 $M_{d,\chi }$
. Briefly speaking, the Virasoro constraints predict that certain intersection numbers on
$M_{d,\chi }$
. Briefly speaking, the Virasoro constraints predict that certain intersection numbers on
 $M_{d,\chi }$
obtained by integrating natural cohomology classes satisfy some explicit universal relations. See [Reference Bojko, Lim and MoreiraBLM, Section 1.3] for the precise statement.
$M_{d,\chi }$
obtained by integrating natural cohomology classes satisfy some explicit universal relations. See [Reference Bojko, Lim and MoreiraBLM, Section 1.3] for the precise statement. -
○ The main theorem of [Reference Pi and ShenPS] is a uniformFootnote 3 minimal generation and freeness result on
 $H^*(M_{d,\chi }, \mathbb {C})$
for all
$H^*(M_{d,\chi }, \mathbb {C})$
for all
 $\chi $
coprime to d; see Theorem 2.2 for a precise and slightly stronger statement. The
$\chi $
coprime to d; see Theorem 2.2 for a precise and slightly stronger statement. The
 $P=C$
conjecture formulated in [Reference Kononov, Pi and ShenKPS] seeks to identify the perverse filtration on the free part of
$P=C$
conjecture formulated in [Reference Kononov, Pi and ShenKPS] seeks to identify the perverse filtration on the free part of
 $H^*(M_{d,\chi }, \mathbb {Q})$
with an explicit Chern filtration defined in terms of the generators. This prediction is also independent of
$H^*(M_{d,\chi }, \mathbb {Q})$
with an explicit Chern filtration defined in terms of the generators. This prediction is also independent of
 $\chi $
.
$\chi $
. -
○ Finally, we remark that the perverse filtration on
 $H^*(M_{d,\chi }, \mathbb {C})$
comes from the ring structure. Indeed, denoting by L the pull-back of the hyperplane class by the Hilbert–Chow morphism, it is completely determined by the multiplication operator L according to [Reference de Cataldo and MigliorinidCM, Proposition 5.2.4].
$H^*(M_{d,\chi }, \mathbb {C})$
comes from the ring structure. Indeed, denoting by L the pull-back of the hyperplane class by the Hilbert–Chow morphism, it is completely determined by the multiplication operator L according to [Reference de Cataldo and MigliorinidCM, Proposition 5.2.4].
2. Tautological classes and relations in
 $A^d(M_{d,\chi })$
$A^d(M_{d,\chi })$
For the remainder of this paper, we assume
![]() $\chi , \chi '$
are coprime to d. This section provides some preliminary results on the cohomology of the moduli spaces
$\chi , \chi '$
are coprime to d. This section provides some preliminary results on the cohomology of the moduli spaces
![]() $M_{d,\chi }$
. We recall the normalized tautological classes and certain tautological relations introduced in [Reference Pi and ShenPS] and prove a first result on the relations in
$M_{d,\chi }$
. We recall the normalized tautological classes and certain tautological relations introduced in [Reference Pi and ShenPS] and prove a first result on the relations in
![]() $A^d(M_{d,\chi })$
.
$A^d(M_{d,\chi })$
.
2.1. Tautological classes
Under the assumption that
![]() $\mathrm {gcd}(d,\chi )=1$
, there exists a universal sheaf [Reference Huybrechts and LehnHL, Theorem 4.6.5] over the product
$\mathrm {gcd}(d,\chi )=1$
, there exists a universal sheaf [Reference Huybrechts and LehnHL, Theorem 4.6.5] over the product
![]() $\mathbb {P}^2 \times M_{d,\chi }$
which we denote by
$\mathbb {P}^2 \times M_{d,\chi }$
which we denote by
![]() $\mathbb {F}$
. For a stable sheaf
$\mathbb {F}$
. For a stable sheaf
![]() $[\mathcal {F}]\in M_{d,\chi }$
, the restriction of
$[\mathcal {F}]\in M_{d,\chi }$
, the restriction of
![]() $\mathbb {F}$
to the fiber
$\mathbb {F}$
to the fiber
![]() $\mathbb {P}^2 \times [\mathcal {F}]$
recovers
$\mathbb {P}^2 \times [\mathcal {F}]$
recovers
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
Consider the two projection maps
![]() $\pi _P$
and
$\pi _P$
and
![]() $\pi _M$
from
$\pi _M$
from
![]() $\mathbb {P}^2 \times M_{d,\chi }$
to its first and second components. One way to obtain natural cohomology classes on
$\mathbb {P}^2 \times M_{d,\chi }$
to its first and second components. One way to obtain natural cohomology classes on
![]() $M_{d,\chi }$
is to take the Chern characters of
$M_{d,\chi }$
is to take the Chern characters of
![]() $\mathbb {F}$
, intersect with classes pulled back from
$\mathbb {F}$
, intersect with classes pulled back from
![]() $\mathbb {P}^2$
and push forward to
$\mathbb {P}^2$
and push forward to
![]() $M_{d,\chi }$
. The choice of
$M_{d,\chi }$
. The choice of
![]() $\mathbb {F}$
is, however, not unique: Any two universal sheaves differ by tensoring with a line bundle pulled back from
$\mathbb {F}$
is, however, not unique: Any two universal sheaves differ by tensoring with a line bundle pulled back from
![]() $M_{d,\chi }$
. We thus conduct a normalization of
$M_{d,\chi }$
. We thus conduct a normalization of
![]() $\mathbb {F}$
as follows.
$\mathbb {F}$
as follows.
For a universal sheaf
![]() $\mathbb {F}$
and a class
$\mathbb {F}$
and a class
we consider the twisted Chern character
and denote by
![]() $\mathrm {ch}_k^\delta (\mathbb {F})$
its degree k-part. For any class
$\mathrm {ch}_k^\delta (\mathbb {F})$
its degree k-part. For any class
![]() $\gamma \in A^*(\mathbb {P}^2)$
, we write
$\gamma \in A^*(\mathbb {P}^2)$
, we write

It is proven in [Reference Pi and ShenPS, Proposition 1.2] that for a fixed
![]() $\mathbb {F}$
, there exists a unique class
$\mathbb {F}$
, there exists a unique class
![]() $\delta _0=\delta _0({\mathbb {F}})$
as above satisfying the normalizing conditions
$\delta _0=\delta _0({\mathbb {F}})$
as above satisfying the normalizing conditions
 $$ \begin{align} \int_H \mathrm{ch}_2^{\delta_0} (\mathbb{F})=0,\;\;\; \int_{\mathbf{1}_{\mathbb{P}^2}} \mathrm{ch}^{\delta_0}_2(\mathbb{F})=0. \end{align} $$
$$ \begin{align} \int_H \mathrm{ch}_2^{\delta_0} (\mathbb{F})=0,\;\;\; \int_{\mathbf{1}_{\mathbb{P}^2}} \mathrm{ch}^{\delta_0}_2(\mathbb{F})=0. \end{align} $$
This class is computed explicitly in [Reference Kononov, Pi and ShenKPS, Proposition 2.1]:
 $$ \begin{align} \delta_0=\left(\frac{3}{2}-\frac{\chi}{d}\right)\cdot H-\frac{1}{d}\left(\left(\frac{3}{2}-\frac{\chi}{d}\right)\int_{H^2}{\mathrm{ch}}_1({\mathbb{F}})+\int_H \mathrm{ch}_2(\mathbb{F})\right). \end{align} $$
$$ \begin{align} \delta_0=\left(\frac{3}{2}-\frac{\chi}{d}\right)\cdot H-\frac{1}{d}\left(\left(\frac{3}{2}-\frac{\chi}{d}\right)\int_{H^2}{\mathrm{ch}}_1({\mathbb{F}})+\int_H \mathrm{ch}_2(\mathbb{F})\right). \end{align} $$
Note that the twisted Chern character
![]() ${\mathrm {ch}}^{\delta _0}({\mathbb {F}})$
does not depend on the choice of
${\mathrm {ch}}^{\delta _0}({\mathbb {F}})$
does not depend on the choice of
![]() ${\mathbb {F}}$
anymore. With this normalizing class, we define the tautological classes
${\mathbb {F}}$
anymore. With this normalizing class, we define the tautological classes
We collect some basic properties of the tautological classes from [Reference Pi and ShenPS, Section 1.2].
Proposition 2.1. Let
![]() $c_k(j)$
be the tautological classes defined by Equation (2.3).
$c_k(j)$
be the tautological classes defined by Equation (2.3).
-
(a) The classes
 $c_k(j)$
do not depend on the choice of a universal sheaf.
$c_k(j)$
do not depend on the choice of a universal sheaf. -
(b) We have
 $$\begin{align*}c_1(0)=0 \in A^0(M_{d,\chi}), \;\;\; c_1(1) = 0 \in A^1(M_{d,\chi}),\;\;\; c_0(1)=d\in A^0(M_{d,\chi}). \end{align*}$$
$$\begin{align*}c_1(0)=0 \in A^0(M_{d,\chi}), \;\;\; c_1(1) = 0 \in A^1(M_{d,\chi}),\;\;\; c_0(1)=d\in A^0(M_{d,\chi}). \end{align*}$$
-
(c) Let
 $\psi _1$
and
$\psi _1$
and
 $\psi _2$
be the two symmetries introduced in Section 1.1. Then we have
$\psi _2$
be the two symmetries introduced in Section 1.1. Then we have  $$\begin{align*}\psi_1^* c_k(j)= c_k(j),\;\;\; \psi_2^* c_k(j) = (-1)^k c_k(j). \end{align*}$$
$$\begin{align*}\psi_1^* c_k(j)= c_k(j),\;\;\; \psi_2^* c_k(j) = (-1)^k c_k(j). \end{align*}$$
The next theorem gives a first result on the structure of
![]() $A^*(M_{d,\chi })$
in terms of the tautological classes. Note that we change the coefficient from
$A^*(M_{d,\chi })$
in terms of the tautological classes. Note that we change the coefficient from
![]() $\mathbb {Q}$
to
$\mathbb {Q}$
to
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
Theorem 2.2 [Reference Pi and ShenPS, Reference YuanY2].
Assume
![]() $d \geq 5$
. We have:
$d \geq 5$
. We have:
-
(a)
 $A^*(M_{d,\chi })$
is generated as a
$A^*(M_{d,\chi })$
is generated as a
 ${\mathbb {C}}$
-algebra by the
${\mathbb {C}}$
-algebra by the
 $3d-7$
classesFootnote
4
of degrees
$3d-7$
classesFootnote
4
of degrees
 $\leq d-2$
: (2.4)
$\leq d-2$
: (2.4) $$ \begin{align} c_0(2),\, c_2(0) \in A^1(M_{d,\chi}), \;\;\; c_{k}(0),\, c_{k-1}(1),\, c_{k-2}(2) \in A^{k-1}(M_{d,\chi}),\;\; 3\leq k \leq d-1. \end{align} $$
$$ \begin{align} c_0(2),\, c_2(0) \in A^1(M_{d,\chi}), \;\;\; c_{k}(0),\, c_{k-1}(1),\, c_{k-2}(2) \in A^{k-1}(M_{d,\chi}),\;\; 3\leq k \leq d-1. \end{align} $$
-
(b) There is no relation among these
 $3d-7$
classes in degrees
$3d-7$
classes in degrees
 $\leq d-1$
.
$\leq d-1$
. -
(c) There are exactly three linearly independent relations in degree d.
We briefly recall the proof of Theorem 2.2: (i) By the results of Beauville [Reference BeauvilleBea] or Markman [Reference MarkmanMar], the ring
![]() $A^*(M_{d,\chi })$
is generated by the tautological classes. (ii) Using the geometry of
$A^*(M_{d,\chi })$
is generated by the tautological classes. (ii) Using the geometry of
![]() $M_{d,\chi }$
, we produce tautological relations that express any tautological class in terms of the
$M_{d,\chi }$
, we produce tautological relations that express any tautological class in terms of the
![]() $3d-7$
classes in Equation (2.4); see the paragraph after Proposition 2.6. (iii) Part (b) and (c) follow from comparing the Betti numbers of
$3d-7$
classes in Equation (2.4); see the paragraph after Proposition 2.6. (iii) Part (b) and (c) follow from comparing the Betti numbers of
![]() $M_{d,\chi }$
with those of Hilbert schemes of points on
$M_{d,\chi }$
with those of Hilbert schemes of points on
![]() $\mathbb {P}^2$
; this is explained in Yuan [Reference YuanY1, Reference YuanY2].
$\mathbb {P}^2$
; this is explained in Yuan [Reference YuanY1, Reference YuanY2].
As we will see, the three relations in
![]() $A^d(M_{d,\chi })$
are the central characters in our proof of Theorem 1.2. By carefully investigating the
$A^d(M_{d,\chi })$
are the central characters in our proof of Theorem 1.2. By carefully investigating the
![]() $\chi $
-dependence of the three relations, we are able to deduce that
$\chi $
-dependence of the three relations, we are able to deduce that
![]() $A^*({M_{d,\chi }})$
are nonisomorphic for different choices of
$A^*({M_{d,\chi }})$
are nonisomorphic for different choices of
![]() $\chi $
unless they are related by the symmetries in Section 1.1.
$\chi $
unless they are related by the symmetries in Section 1.1.
Remark 2.3. The choice of the normalization (2.1) and the shift in degrees of the Chern character in Equation (2.3) are motivated by the
![]() $P=C$
conjecture [Reference Kononov, Pi and ShenKPS]. Roughly speaking, the
$P=C$
conjecture [Reference Kononov, Pi and ShenKPS]. Roughly speaking, the
![]() $P=C$
conjecture predicts that the Chern grading of the tautological generators
$P=C$
conjecture predicts that the Chern grading of the tautological generators
![]() $c_k(j)$
coincides with its perversity; this gives a conjectural explicit description of the perverse filtration on
$c_k(j)$
coincides with its perversity; this gives a conjectural explicit description of the perverse filtration on
![]() $A^{*\leq d-2}(M_{d,\chi })$
in terms of Equation (2.4). See [Reference Kononov, Pi and ShenKPS, Conjecture 0.3 and Proposition 1.2] for details.
$A^{*\leq d-2}(M_{d,\chi })$
in terms of Equation (2.4). See [Reference Kononov, Pi and ShenKPS, Conjecture 0.3 and Proposition 1.2] for details.
2.2. Tautological relations
We recall in this section certain tautological relations [Reference Pi and ShenPS, Section 1.2] on the cohomology of
![]() $M_{d,\chi }$
. By the symmetry (a) in Section 1.1, we may assume that
$M_{d,\chi }$
. By the symmetry (a) in Section 1.1, we may assume that
![]() $0 < \chi < d$
so that any
$0 < \chi < d$
so that any
![]() $\mathcal {F} \in M_{d,\chi }$
satisfies
$\mathcal {F} \in M_{d,\chi }$
satisfies
![]() $0< \mu (\mathcal {F}) <1$
.
$0< \mu (\mathcal {F}) <1$
.
Consider the triple product ![]() , where
, where
![]() $\check {\mathbb {P}}^2$
is the dual projective space parametrizing lines in
$\check {\mathbb {P}}^2$
is the dual projective space parametrizing lines in
![]() $\mathbb {P}^2$
. Let
$\mathbb {P}^2$
. Let
![]() $\pi _R : Y \to \check {\mathbb {P}}^2$
be the third projection. We write
$\pi _R : Y \to \check {\mathbb {P}}^2$
be the third projection. We write
![]() $p= \pi _P \times \pi _M, \, q = \pi _P \times \pi _R$
and
$p= \pi _P \times \pi _M, \, q = \pi _P \times \pi _R$
and
![]() $r = \pi _M \times \pi _R$
:
$r = \pi _M \times \pi _R$
:

Let
![]() $Z\subset \mathbb {P}^2\times \check {\mathbb {P}}^2$
be the incidence subscheme, and let
$Z\subset \mathbb {P}^2\times \check {\mathbb {P}}^2$
be the incidence subscheme, and let
![]() $\mathcal {O}_Z$
be its structure sheaf. For a fixed universal sheaf
$\mathcal {O}_Z$
be its structure sheaf. For a fixed universal sheaf
![]() $\mathbb {F}$
on
$\mathbb {F}$
on
![]() $M_{d,\chi }$
, we consider the complex
$M_{d,\chi }$
, we consider the complex
The projection
![]() $r: Y \to M_{d,\chi } \times \check {\mathbb {P}}^2$
is a trivial
$r: Y \to M_{d,\chi } \times \check {\mathbb {P}}^2$
is a trivial
![]() $\mathbb {P}^2$
-bundle, so the derived push-forward
$\mathbb {P}^2$
-bundle, so the derived push-forward
admits a three-term resolution
![]() $0\to K^0 \to K^1 \to K^2 \to 0$
by vector bundles.
$0\to K^0 \to K^1 \to K^2 \to 0$
by vector bundles.
Lemma 2.4. For
![]() $n\in \{1,2,3\}$
, we can choose
$n\in \{1,2,3\}$
, we can choose
![]() $K^i$
with
$K^i$
with
![]() $K^0 = K^2 =0$
and
$K^0 = K^2 =0$
and
![]() $K^1$
free of rank d.
$K^1$
free of rank d.
Proof. This is [Reference Pi and ShenPS, Lemma 2.4]; we briefly recall the proof here. Take a point
where
![]() $[L]\in \check {{\mathbb {P}}}^2$
corresponds to the line
$[L]\in \check {{\mathbb {P}}}^2$
corresponds to the line
![]() $L\subseteq {\mathbb {P}}^2$
. Over the point P, cohomology of the complex
$L\subseteq {\mathbb {P}}^2$
. Over the point P, cohomology of the complex
![]() $K^0(P) \to K^1(P)\to K^2(P)$
computes the extension groups
$K^0(P) \to K^1(P)\to K^2(P)$
computes the extension groups
Note that
![]() $\mu (\mathcal {O}_{L}(-n))=1-n$
. By stability and Serre duality, one checks that
$\mu (\mathcal {O}_{L}(-n))=1-n$
. By stability and Serre duality, one checks that
as long as
![]() $n\in \{1,2,3\}$
. This implies
$n\in \{1,2,3\}$
. This implies
![]() $Rr_*\mathcal {H}(n)$
can be represented by a single vector bundle
$Rr_*\mathcal {H}(n)$
can be represented by a single vector bundle
![]() $K^1$
concentrated in degree
$K^1$
concentrated in degree
![]() $1$
, whose rank is d by a Hirzebruch–Riemann–Roch calculation.
$1$
, whose rank is d by a Hirzebruch–Riemann–Roch calculation.
It follows that
![]() $-Rr_* \mathcal {H}(n)$
is a rank d vector bundle on
$-Rr_* \mathcal {H}(n)$
is a rank d vector bundle on
![]() $M_{d,\chi } \times \check {\mathbb {P}}^2$
, whence
$M_{d,\chi } \times \check {\mathbb {P}}^2$
, whence
Corollary 2.5. For
![]() $\ell \geq d+1$
and
$\ell \geq d+1$
and
![]() $n\in \{1,2,3\}$
, we have
$n\in \{1,2,3\}$
, we have
Recall that
![]() $\mathcal {H}(n)$
is defined by Equation (2.5) in terms of a fixed universal sheaf
$\mathcal {H}(n)$
is defined by Equation (2.5) in terms of a fixed universal sheaf
![]() $\mathbb {F}$
. If we replace
$\mathbb {F}$
. If we replace
![]() $\mathbb {F}$
by
$\mathbb {F}$
by
with L a fractional line bundle over
![]() $M_{d,\chi }$
, then according to Equation (2.5) and the projection formula, the vector bundle
$M_{d,\chi }$
, then according to Equation (2.5) and the projection formula, the vector bundle
![]() $-Rr_*\mathcal {H}(n)$
is replaced by its tensor with the dual line bundle
$-Rr_*\mathcal {H}(n)$
is replaced by its tensor with the dual line bundle
![]() $\pi _M^* L^\vee $
. Using a formal argument involving Chern roots, one checks that the identity (2.6) also holds for
$\pi _M^* L^\vee $
. Using a formal argument involving Chern roots, one checks that the identity (2.6) also holds for
![]() $\mathbb {F}'$
.
$\mathbb {F}'$
.
In particular, we choose the fractional line bundle L to have first Chern classFootnote 5
 $$\begin{align*}c_1(L)=-\frac{1}{d}\left(\left(\frac{3}{2}-\frac{\chi}{d}\right)c_0(2)+\int_H \mathrm{ch}_2(\mathbb{F})\right) \end{align*}$$
$$\begin{align*}c_1(L)=-\frac{1}{d}\left(\left(\frac{3}{2}-\frac{\chi}{d}\right)c_0(2)+\int_H \mathrm{ch}_2(\mathbb{F})\right) \end{align*}$$
so that the normalizing class (2.2) for
![]() $\mathbb {F}'$
is given by
$\mathbb {F}'$
is given by
![]() $\delta _0({\mathbb {F}}')=\left (\frac {3}{2}-\frac {\chi }{d}\right )\cdot H$
. Now, we apply Equation (2.6) to
$\delta _0({\mathbb {F}}')=\left (\frac {3}{2}-\frac {\chi }{d}\right )\cdot H$
. Now, we apply Equation (2.6) to
![]() $\mathbb {F}'$
. The Chern classes in Equation (2.6) can be expressed in terms of the Chern character
$\mathbb {F}'$
. The Chern classes in Equation (2.6) can be expressed in terms of the Chern character
![]() $\mathrm {ch}(Rr_*\mathcal {H}(n))$
, which is computed by the Grothendieck–Riemann–Roch theorem:
$\mathrm {ch}(Rr_*\mathcal {H}(n))$
, which is computed by the Grothendieck–Riemann–Roch theorem:
 $$ \begin{align*} \mathrm{ch}(Rr_*\mathcal{H}(n))&=r_*(\mathrm{ch}(\mathcal{H}(n))\cdot \mathrm{td}({\mathbb{P}}^2)) \\ &=r_*(\mathrm{ch}(p^*{\mathbb{F}'}^\vee)\cdot \mathrm{ch}(q^*\mathcal{O}_Z\otimes \pi_P^* \mathcal{O}_{{\mathbb{P}}^2}(-n))\cdot \mathrm{td}({\mathbb{P}}^2)). \end{align*} $$
$$ \begin{align*} \mathrm{ch}(Rr_*\mathcal{H}(n))&=r_*(\mathrm{ch}(\mathcal{H}(n))\cdot \mathrm{td}({\mathbb{P}}^2)) \\ &=r_*(\mathrm{ch}(p^*{\mathbb{F}'}^\vee)\cdot \mathrm{ch}(q^*\mathcal{O}_Z\otimes \pi_P^* \mathcal{O}_{{\mathbb{P}}^2}(-n))\cdot \mathrm{td}({\mathbb{P}}^2)). \end{align*} $$
We denote by
![]() $\beta $
the class of a line on
$\beta $
the class of a line on
![]() $\check {\mathbb {P}}^2$
. Expanding the right-hand side of the above equation, Corollary 2.5 then gives relations in
$\check {\mathbb {P}}^2$
. Expanding the right-hand side of the above equation, Corollary 2.5 then gives relations in
![]() $A^*(M_{d,\chi } \times \check {\mathbb {P}}^2)$
:
$A^*(M_{d,\chi } \times \check {\mathbb {P}}^2)$
:
Proposition 2.6. For every
![]() $\ell \geq d+1$
and
$\ell \geq d+1$
and
![]() $n\in \{1,2,3\}$
, the following identity holds:
$n\in \{1,2,3\}$
, the following identity holds:
 $$ \begin{align} \sum_{\mathbf{m}} \prod_{s=1}^\ell \frac{((s-1)!)^{m_s}}{(m_s)!}\left( \pi_M^* A_{s}- \sum_{0\leq i\leq 2}\frac{\pi_R^*\beta^i}{i!}(-1)^i \pi_M^* B_{s-i}\right)^{m_s}=0. \end{align} $$
$$ \begin{align} \sum_{\mathbf{m}} \prod_{s=1}^\ell \frac{((s-1)!)^{m_s}}{(m_s)!}\left( \pi_M^* A_{s}- \sum_{0\leq i\leq 2}\frac{\pi_R^*\beta^i}{i!}(-1)^i \pi_M^* B_{s-i}\right)^{m_s}=0. \end{align} $$
Here, the first sum is over all
![]() $\ell $
-tuple of nonnegative integers
$\ell $
-tuple of nonnegative integers
![]() $\mathbf {m}=(m_1,m_2,\ldots , m_\ell )$
such that
$\mathbf {m}=(m_1,m_2,\ldots , m_\ell )$
such that
![]() $m_1+2m_2+\cdots +\ell m_\ell =\ell $
, and writing
$m_1+2m_2+\cdots +\ell m_\ell =\ell $
, and writing ![]() , the terms
, the terms
![]() $A_s, B_s$
are given by
$A_s, B_s$
are given by

Proof. The proof is essentially the same as [Reference Pi and ShenPS, Proposition 2.6], except that we use the normalized Chern character
![]() $\mathrm {ch}^{\delta _0}({\mathbb {F}'}^\vee )=\mathrm {ch}({\mathbb {F}'}^\vee )\cdot \exp (-\delta _0)$
. The convoluted formula results from applying Newton’s identity to express Chern classes in the Chern characters, and the class
$\mathrm {ch}^{\delta _0}({\mathbb {F}'}^\vee )=\mathrm {ch}({\mathbb {F}'}^\vee )\cdot \exp (-\delta _0)$
. The convoluted formula results from applying Newton’s identity to express Chern classes in the Chern characters, and the class
![]() $\beta $
comes from
$\beta $
comes from
![]() $\mathrm {ch}(q^* \mathcal {O}_Z)$
. See also [Reference Kononov, Pi and ShenKPS, Proposition 2.7] for an explicit version for
$\mathrm {ch}(q^* \mathcal {O}_Z)$
. See also [Reference Kononov, Pi and ShenKPS, Proposition 2.7] for an explicit version for
![]() $M_{4,1}$
.
$M_{4,1}$
.
To obtain relations in
![]() $A^*(M_{d,\chi })$
, we first take the identity (2.7) for some
$A^*(M_{d,\chi })$
, we first take the identity (2.7) for some
![]() $\ell \geq d+1$
; this gives a relation in
$\ell \geq d+1$
; this gives a relation in
![]() $A^\ell (M_{d,\chi } \times \check {\mathbb {P}}^2)$
. Then we multiply it by
$A^\ell (M_{d,\chi } \times \check {\mathbb {P}}^2)$
. Then we multiply it by
![]() $\pi _R^* (\beta ^j)$
and push forward to
$\pi _R^* (\beta ^j)$
and push forward to
![]() $M_{d,\chi }$
, where
$M_{d,\chi }$
, where
![]() $0\leq j \leq 2$
. This produces a relation in
$0\leq j \leq 2$
. This produces a relation in
![]() $A^{\ell +j-2}(M_{d,\chi })$
among the tautological classes (2.3). The procedure is explained in detail in [Reference Pi and ShenPS, Section 2.3] and the paragraph before it. Indeed, as a key step in the proof of Theorem 2.2(a), it is shown in [Reference Pi and ShenPS, Section 2.3] that the relations produced by Proposition 2.6 express all the tautological classes (2.3) in terms of the
$A^{\ell +j-2}(M_{d,\chi })$
among the tautological classes (2.3). The procedure is explained in detail in [Reference Pi and ShenPS, Section 2.3] and the paragraph before it. Indeed, as a key step in the proof of Theorem 2.2(a), it is shown in [Reference Pi and ShenPS, Section 2.3] that the relations produced by Proposition 2.6 express all the tautological classes (2.3) in terms of the
![]() $3d-7$
generators (2.4).
$3d-7$
generators (2.4).
2.3. Three relations in
 $A^{d}(M_{d,\chi })$
$A^{d}(M_{d,\chi })$
The goal of this section is to prove the following result:
Proposition 2.7. For
![]() $d\geq 5$
, the three linearly independent relations in
$d\geq 5$
, the three linearly independent relations in
![]() $A^d(M_{d,\chi })$
, cf. Theorem 2.2(c), can be produced by Proposition 2.6.
$A^d(M_{d,\chi })$
, cf. Theorem 2.2(c), can be produced by Proposition 2.6.
We first introduce some notations for the rest of the paper. Let
![]() $T^k$
be the linear space spanned by tautological classes in degree k, that is,
$T^k$
be the linear space spanned by tautological classes in degree k, that is,
Let

be the span of the
![]() $3d-7$
tautological generators in Equation (2.4), and let
$3d-7$
tautological generators in Equation (2.4), and let
We denote by
![]() $\mathbb {C}[T]$
the symmetric algebra in T (i.e., the free algebra generated by the
$\mathbb {C}[T]$
the symmetric algebra in T (i.e., the free algebra generated by the
![]() $3d-7$
tautological generators), and by
$3d-7$
tautological generators), and by
![]() $\mathbb {C}[T]^k$
its graded piece of degree k. Similarly, we write
$\mathbb {C}[T]^k$
its graded piece of degree k. Similarly, we write
![]() ${\mathbb {C}}[T^+]$
for the symmetric algebra on
${\mathbb {C}}[T^+]$
for the symmetric algebra on
![]() $T^+$
.
$T^+$
.
Furthermore, we endow the basis of
![]() $T^+$
with a total ordering
$T^+$
with a total ordering
![]() $\prec $
as follows: First order the basis by cohomological degrees; within each degree, we order by the Chern grading of the basis. In a precise way, this means
$\prec $
as follows: First order the basis by cohomological degrees; within each degree, we order by the Chern grading of the basis. In a precise way, this means
![]() $c_k(j) \prec c_{k'}(j')$
if and only if
$c_k(j) \prec c_{k'}(j')$
if and only if
![]() $k+j-1<k'+j'-1$
, or
$k+j-1<k'+j'-1$
, or
![]() $k+j-1=k'+j'-1$
and
$k+j-1=k'+j'-1$
and
![]() $k<k'$
. Finally, we endow monomials in each degree of
$k<k'$
. Finally, we endow monomials in each degree of
![]() $\mathbb {C}[T^+]$
the lexicographical order induced by the total ordering
$\mathbb {C}[T^+]$
the lexicographical order induced by the total ordering
![]() $\prec $
on
$\prec $
on
![]() $T^+$
. In this way, we can talk about the leading term of a polynomial in
$T^+$
. In this way, we can talk about the leading term of a polynomial in
![]() $\mathbb {C}[T^+]$
, as well as in
$\mathbb {C}[T^+]$
, as well as in
![]() $\mathbb {C}[T]$
.
$\mathbb {C}[T]$
.
We have graded algebra homomorphisms
Theorem 2.2 states that the homomorphism
![]() ${\mathbb {C}}[T]\to A^\ast (M_{d,\chi })$
is surjective, that it is an isomorphism up to degree
${\mathbb {C}}[T]\to A^\ast (M_{d,\chi })$
is surjective, that it is an isomorphism up to degree
![]() $d-1$
and that
$d-1$
and that
![]() $\ker \!\big ({\mathbb {C}}[T]^d\to A^d(M_{d,\chi })\big )$
is 3-dimensional. A relation is by definition an element in the kernel of
$\ker \!\big ({\mathbb {C}}[T]^d\to A^d(M_{d,\chi })\big )$
is 3-dimensional. A relation is by definition an element in the kernel of
![]() ${\mathbb {C}}[T]\to A^\ast (M_{d,\chi })$
or
${\mathbb {C}}[T]\to A^\ast (M_{d,\chi })$
or
![]() ${\mathbb {C}}[T^+]\to A^\ast (M_{d,\chi })$
.
${\mathbb {C}}[T^+]\to A^\ast (M_{d,\chi })$
.
With the above setup, Theorem 2.2 (b) and (c) are equivalent to the following.Footnote 6
Proposition 2.8. For
![]() $d\geq 5$
, we have
$d\geq 5$
, we have
 $$\begin{align*}\dim A^k(M_{d,\chi}) = \begin{cases} \dim \mathbb{C}[T^+]^k, \quad & k \leq d-2,\\ \dim \mathbb{C}[T^+]^k-3, \quad &k = d-1,\\ \dim \mathbb{C}[T^+]^k -12, \;\; &k=d. \end{cases} \end{align*}$$
$$\begin{align*}\dim A^k(M_{d,\chi}) = \begin{cases} \dim \mathbb{C}[T^+]^k, \quad & k \leq d-2,\\ \dim \mathbb{C}[T^+]^k-3, \quad &k = d-1,\\ \dim \mathbb{C}[T^+]^k -12, \;\; &k=d. \end{cases} \end{align*}$$
Since
![]() $\dim {\mathbb {C}}[T^+]^d=\dim {\mathbb {C}}[T]^d+9$
, to prove Proposition 2.7 it suffices to produce 12 linearly independent relations in
$\dim {\mathbb {C}}[T^+]^d=\dim {\mathbb {C}}[T]^d+9$
, to prove Proposition 2.7 it suffices to produce 12 linearly independent relations in
![]() $\mathbb {C}[T^+]^d$
from Proposition 2.6. These 12 relations in degree d are produced in the following three ways:
$\mathbb {C}[T^+]^d$
from Proposition 2.6. These 12 relations in degree d are produced in the following three ways:
-
(a) Take
 $\ell = d+1$
in Equation (2.7), we get the vanishing of a cohomology class in
$\ell = d+1$
in Equation (2.7), we get the vanishing of a cohomology class in
 $M_{d, \chi }\times \check {{\mathbb {P}}}^2$
. Pushing forward to
$M_{d, \chi }\times \check {{\mathbb {P}}}^2$
. Pushing forward to
 $M_{d, \chi }$
yields a relation
$M_{d, \chi }$
yields a relation
 $R_{{(a)}}^n\in {\mathbb {C}}[T^+]^{d-1}$
for
$R_{{(a)}}^n\in {\mathbb {C}}[T^+]^{d-1}$
for
 $n=1,2,3$
. Each of these three relations produces two relations in degree d, namely
$n=1,2,3$
. Each of these three relations produces two relations in degree d, namely
 $c_2(0)R_{(a)}^n$
and
$c_2(0)R_{(a)}^n$
and
 $c_0(2)R_{(a)}^n$
.
$c_0(2)R_{(a)}^n$
. -
(b) Take
 $\ell = d+1$
in Equation (2.7), multiply by
$\ell = d+1$
in Equation (2.7), multiply by
 $\pi _R^* (\beta )$
and push forward to
$\pi _R^* (\beta )$
and push forward to
 $M_{d, \chi }$
. This produces three relations
$M_{d, \chi }$
. This produces three relations
 $R_{(b)}^n\in {\mathbb {C}}[T^+]^{d}$
for
$R_{(b)}^n\in {\mathbb {C}}[T^+]^{d}$
for
 $n=1,2,3$
.
$n=1,2,3$
. -
(c) Take
 $\ell = d+2$
in Equation (2.7) and push forward to
$\ell = d+2$
in Equation (2.7) and push forward to
 $M_{d, \chi }$
. This produces three relations
$M_{d, \chi }$
. This produces three relations
 $R_{(c)}^n\in {\mathbb {C}}[T^+]^{d}$
for
$R_{(c)}^n\in {\mathbb {C}}[T^+]^{d}$
for
 $n=1,2,3$
.
$n=1,2,3$
.
We now proceed to argue that these 12 relations are linearly independent. It can be checked, cf. det1 in the Mathematica file and [Reference Pi and ShenPS, Section 2.3], that under the assumption
![]() $\mathrm {gcd}(d,\chi )=1$
, the
$\mathrm {gcd}(d,\chi )=1$
, the
![]() $3\times 3$
matrix of coefficients of
$3\times 3$
matrix of coefficients of
![]() $c_{d}(0), c_{d-1}(1), c_{d-2}(2)$
in the three relations
$c_{d}(0), c_{d-1}(1), c_{d-2}(2)$
in the three relations
![]() $R_{(a)}^1, R_{(a)}^2, R_{(a)}^3$
is nonsingular; in fact, it has determinant
$R_{(a)}^1, R_{(a)}^2, R_{(a)}^3$
is nonsingular; in fact, it has determinant
In particular, equations
![]() $R_{(a)}^n$
can be used to express
$R_{(a)}^n$
can be used to express
![]() $c_{d}(0), c_{d-1}(1), c_{d-2}(2)$
in terms of the tautological generators (2.4). Multiplying these equations with
$c_{d}(0), c_{d-1}(1), c_{d-2}(2)$
in terms of the tautological generators (2.4). Multiplying these equations with
![]() $c_2(0), c_0(2)$
, we obtain six relations in
$c_2(0), c_0(2)$
, we obtain six relations in
![]() $\mathbb {C}[T^+]^{d}$
. These are still linearly independent since the
$\mathbb {C}[T^+]^{d}$
. These are still linearly independent since the
![]() $6\times 6$
matrix given by the coefficients of the monomials
$6\times 6$
matrix given by the coefficients of the monomials
is invertible with determinant
![]() $\texttt {det1}^2$
.
$\texttt {det1}^2$
.
We consider now the six relations
![]() $R_{(b)}^n, R_{(c)}^n$
, for
$R_{(b)}^n, R_{(c)}^n$
, for
![]() $n=1,2,3$
and the set of monomials
$n=1,2,3$
and the set of monomials
The
![]() $6\times 6$
matrix of coefficients of
$6\times 6$
matrix of coefficients of
![]() $\mathsf {Mon}_2$
in these six relations is nonsingular. Indeed, a direct computation (cf. det2 in the Mathematica file) gives the determinant
$\mathsf {Mon}_2$
in these six relations is nonsingular. Indeed, a direct computation (cf. det2 in the Mathematica file) gives the determinant
It follows that the six relations
![]() $R_{(b)}^n$
and
$R_{(b)}^n$
and
![]() $R_{(c)}^n$
with
$R_{(c)}^n$
with
![]() $n\in \{1,2,3\}$
are linearly independent.
$n\in \{1,2,3\}$
are linearly independent.
Finally, we note that the monomials in
![]() $\mathsf {Mon}_2$
do not appear in the relations of the form
$\mathsf {Mon}_2$
do not appear in the relations of the form
![]() $c_2(0)R_{(a)}^n, c_0(2)R_{(a)}^n$
, so the
$c_2(0)R_{(a)}^n, c_0(2)R_{(a)}^n$
, so the
![]() $12\times 12$
matrix of coefficients of monomials
$12\times 12$
matrix of coefficients of monomials
![]() $\mathsf {Mon}_1\cup \mathsf {Mon}_2$
in the 12 relations obtained by (a), (b), (c) is also nonsingular. We conclude that these 12 relations are all linearly independent, completing the proof of Proposition 2.7.
$\mathsf {Mon}_1\cup \mathsf {Mon}_2$
in the 12 relations obtained by (a), (b), (c) is also nonsingular. We conclude that these 12 relations are all linearly independent, completing the proof of Proposition 2.7.
To explicitly obtain the three relations in
![]() ${\mathbb {C}}[T]^d$
, we proceed as follows. We use the relations
${\mathbb {C}}[T]^d$
, we proceed as follows. We use the relations
![]() $R_{(a)}^n$
to express
$R_{(a)}^n$
to express
![]() $c_{d}(0), c_{d-1}(1), c_{d-2}(2)$
in terms of lower degree generators in the image of
$c_{d}(0), c_{d-1}(1), c_{d-2}(2)$
in terms of lower degree generators in the image of
![]() ${\mathbb {C}}[T]$
; we then use
${\mathbb {C}}[T]$
; we then use
![]() $R_{(b)}^1, R_{(c)}^1, R_{(c)}^2$
to write
$R_{(b)}^1, R_{(c)}^1, R_{(c)}^2$
to write
![]() $c_{d+1}(0), c_{d}(1), c_{d-1}(2)$
in terms of the tautological generators. Finally, plugging these into the other three relations
$c_{d+1}(0), c_{d}(1), c_{d-1}(2)$
in terms of the tautological generators. Finally, plugging these into the other three relations
yields the three relations in
![]() ${\mathbb {C}}[T]^d$
. By the nonvanishing of det2, the row-echelon form (with respect to the ordering
${\mathbb {C}}[T]^d$
. By the nonvanishing of det2, the row-echelon form (with respect to the ordering
![]() $\prec $
of monomials) of this system produces three relations
$\prec $
of monomials) of this system produces three relations
![]() $R_1, R_2, R_3$
such that
$R_1, R_2, R_3$
such that
A truncated version (see Remark 3.2) of these relations is implemented in the Mathematica file as TruncRelations.
3. Truncated relations and proof of the main result
In this section, we will prove the main result of this paper, Theorem 1.2. By the symmetry (a) in Section 1.1, we may assume without loss of generality that
![]() $0<\chi ,\, \chi '<d$
. Note that when
$0<\chi ,\, \chi '<d$
. Note that when
![]() $d<5$
there is nothing to prove, so we assume as well that
$d<5$
there is nothing to prove, so we assume as well that
![]() $d\geq 5$
. Suppose that there is an isomorphism of graded
$d\geq 5$
. Suppose that there is an isomorphism of graded
![]() ${\mathbb {C}}$
-algebras
${\mathbb {C}}$
-algebras
![]() $\phi \colon A^\ast (M_{d, \chi })\to A^\ast (M_{d, \chi '})$
. We first remark that
$\phi \colon A^\ast (M_{d, \chi })\to A^\ast (M_{d, \chi '})$
. We first remark that
![]() $\phi $
can be uniquely lifted to the free algebra
$\phi $
can be uniquely lifted to the free algebra
![]() ${\mathbb {C}}[T]$
, that is, there exists a map
${\mathbb {C}}[T]$
, that is, there exists a map
![]() $\widetilde {\phi }$
fitting into the diagram
$\widetilde {\phi }$
fitting into the diagram

Such unique lift exists since the cohomology is freely generated up to degree
![]() $d-2$
, where the tautological generators (2.4) lie. More precisely, the lift is defined by
$d-2$
, where the tautological generators (2.4) lie. More precisely, the lift is defined by
By abuse of notation, we write
![]() $\phi $
also for the lifted graded ring isomorphism. We will show that unless
$\phi $
also for the lifted graded ring isomorphism. We will show that unless
![]() $\chi \equiv \pm \chi '\ \mod d$
, there is no such lift respecting the three relations in degree d, that is, that sends the three-dimensional subspace
$\chi \equiv \pm \chi '\ \mod d$
, there is no such lift respecting the three relations in degree d, that is, that sends the three-dimensional subspace
Remark 3.1. A graded ring endomorophism of
![]() ${\mathbb {C}}[T]$
is defined by an element of
${\mathbb {C}}[T]$
is defined by an element of
 $$\begin{align*}\prod_{k=1}^{d-2}\operatorname{Hom}\big(T^k, {\mathbb{C}}[T]^k\big)\,.\end{align*}$$
$$\begin{align*}\prod_{k=1}^{d-2}\operatorname{Hom}\big(T^k, {\mathbb{C}}[T]^k\big)\,.\end{align*}$$
For
![]() $d=5$
, the space above has dimension
$d=5$
, the space above has dimension
![]() $2\times 2+3\times 6+3\times 13=61$
. On the other hand, a three-dimensional subspace of
$2\times 2+3\times 6+3\times 13=61$
. On the other hand, a three-dimensional subspace of
![]() ${\mathbb {C}}[T]^d$
defines a point in the Grassmannian
${\mathbb {C}}[T]^d$
defines a point in the Grassmannian
![]() $\mathsf {Gr}\big (3, {\mathbb {C}}[T]^d\big )$
, which has dimension
$\mathsf {Gr}\big (3, {\mathbb {C}}[T]^d\big )$
, which has dimension
![]() $3\times (45-3)=126$
for
$3\times (45-3)=126$
for
![]() $d=5$
. Thus, we expect no graded ring endomorphism that takes a general point in
$d=5$
. Thus, we expect no graded ring endomorphism that takes a general point in
![]() $\mathsf {Gr}(3, \mathbb {C}[T]^d)$
to another.
$\mathsf {Gr}(3, \mathbb {C}[T]^d)$
to another.
Let
![]() $R_1, R_2, R_3\in {\mathbb {C}}[T]^d$
be the three relations in Equation (2.8); these span
$R_1, R_2, R_3\in {\mathbb {C}}[T]^d$
be the three relations in Equation (2.8); these span
![]() $\ker \Big ({\mathbb {C}}[T]^d\to A^d(M_{d, \chi })\Big )$
and are such that the matrix
$\ker \Big ({\mathbb {C}}[T]^d\to A^d(M_{d, \chi })\Big )$
and are such that the matrix
![]() $(R_1\; R_2\; R_3)^{\mathsf {T}}$
is in row echelon form with respect to the total ordering introduced in Section 2.3 on the basis of
$(R_1\; R_2\; R_3)^{\mathsf {T}}$
is in row echelon form with respect to the total ordering introduced in Section 2.3 on the basis of
![]() ${\mathbb {C}}[T]^d$
. Similarly, we define
${\mathbb {C}}[T]^d$
. Similarly, we define
![]() $R_1', R_2', R_3'$
to be the relations in
$R_1', R_2', R_3'$
to be the relations in
![]() ${\mathbb {C}}[T]^d$
which come from
${\mathbb {C}}[T]^d$
which come from
![]() $M_{d,\chi '}$
. Since
$M_{d,\chi '}$
. Since
![]() $\phi :{\mathbb {C}}[T]^d\xrightarrow {\sim } {\mathbb {C}}[T]^d$
preserves the three-dimensional kernels, it induces an invertible matrix
$\phi :{\mathbb {C}}[T]^d\xrightarrow {\sim } {\mathbb {C}}[T]^d$
preserves the three-dimensional kernels, it induces an invertible matrix
such that
 $$ \begin{align} \phi(R_i)=\sum_{j=1}^3 s_{ij}R_j'\,. \end{align} $$
$$ \begin{align} \phi(R_i)=\sum_{j=1}^3 s_{ij}R_j'\,. \end{align} $$
Step 1: truncating relations
We start by truncating the relations
![]() $R_i$
by looking only at the terms which are obtained as a product of a generator of degree
$R_i$
by looking only at the terms which are obtained as a product of a generator of degree
![]() $d-2$
with a generator of degree
$d-2$
with a generator of degree
![]() $2$
. In other words, we consider the projection of
$2$
. In other words, we consider the projection of
![]() $R_i$
to
$R_i$
to
![]() $T^2\otimes T^{d-2}\subseteq {\mathbb {C}}[T]^d$
and regard it as a
$T^2\otimes T^{d-2}\subseteq {\mathbb {C}}[T]^d$
and regard it as a
![]() $3\times 3$
matrix
$3\times 3$
matrix
![]() $M_i$
by identifying
$M_i$
by identifying
This is implemented in the Mathematica file as TopRelations[d,chi]. The identification with a
![]() $3\times 3$
matrix uses the ordered basis for
$3\times 3$
matrix uses the ordered basis for
![]() $T^2, T^{d-2}$
given by the generators from Section 2.3.
$T^2, T^{d-2}$
given by the generators from Section 2.3.
More concretely,
where
![]() $[c_{3-s}(s)c_{d-1-t}(t)]$
means reading off the corresponding coefficient with respect to the monomial basis. The matrices
$[c_{3-s}(s)c_{d-1-t}(t)]$
means reading off the corresponding coefficient with respect to the monomial basis. The matrices
![]() $M_1, M_2, M_3$
can be explicitly calculated as follows:
$M_1, M_2, M_3$
can be explicitly calculated as follows:
 $$ \begin{align*} M_1&=\begin{bmatrix}1& 0& 0\\ 0& 0& \frac{(d - 2) (d-2\chi) \chi (d - \chi)}{8 d^3}\\[3pt] \frac{d - 4}{8 d - 16}& \frac{(d-2\chi) \chi (\chi-d)}{2 (d - 2) d^3}& \frac{(-6 \chi - 1) d^5 + (6 \chi^2 + 6 \chi + 3) d^4 + 18 \chi^2 d^3 - (48 \chi^3 + 48 \chi^2) d^2 + (24 \chi^4 + 96 \chi^3) d - 48 \chi^4}{32 (d - 2) d^4}\end{bmatrix},\\M_2&=\begin{bmatrix}0& 1& 0\\ 1& 0& \frac{(-6 \chi - 1) d^2 + (6 \chi^2 + 12 \chi) d - 12 \chi^2}{8 d^2}\\[3pt] 0&\frac{24 \chi^2-24 \chi d-d^3+2 d^2}{8 (d-2) d^2}&\frac{\chi \left(d^2+8 d-16\right) (2 \chi-d) (d-\chi)}{8 (d-2) d^3}\end{bmatrix}, \quad \: M_3=\begin{bmatrix}0& 0& 1\\ 0& 0& 0\\ \frac{2}{d-2}&0&\frac{12 \chi^2 - 12 \chi d - d^2}{8 (d-2) d}\end{bmatrix}. \end{align*} $$
$$ \begin{align*} M_1&=\begin{bmatrix}1& 0& 0\\ 0& 0& \frac{(d - 2) (d-2\chi) \chi (d - \chi)}{8 d^3}\\[3pt] \frac{d - 4}{8 d - 16}& \frac{(d-2\chi) \chi (\chi-d)}{2 (d - 2) d^3}& \frac{(-6 \chi - 1) d^5 + (6 \chi^2 + 6 \chi + 3) d^4 + 18 \chi^2 d^3 - (48 \chi^3 + 48 \chi^2) d^2 + (24 \chi^4 + 96 \chi^3) d - 48 \chi^4}{32 (d - 2) d^4}\end{bmatrix},\\M_2&=\begin{bmatrix}0& 1& 0\\ 1& 0& \frac{(-6 \chi - 1) d^2 + (6 \chi^2 + 12 \chi) d - 12 \chi^2}{8 d^2}\\[3pt] 0&\frac{24 \chi^2-24 \chi d-d^3+2 d^2}{8 (d-2) d^2}&\frac{\chi \left(d^2+8 d-16\right) (2 \chi-d) (d-\chi)}{8 (d-2) d^3}\end{bmatrix}, \quad \: M_3=\begin{bmatrix}0& 0& 1\\ 0& 0& 0\\ \frac{2}{d-2}&0&\frac{12 \chi^2 - 12 \chi d - d^2}{8 (d-2) d}\end{bmatrix}. \end{align*} $$
Remark 3.2. To compute these matrices and also the extended matrices that will appear later in Section 3.3, we follow the strategy described in the previous section. Note that the truncation of the relations
![]() $R_{(a)}^n, R_{(b)}^n, R_{(c)}^n$
can be computed since only finitely many terms of Equation (2.7) contribute. For instance, for
$R_{(a)}^n, R_{(b)}^n, R_{(c)}^n$
can be computed since only finitely many terms of Equation (2.7) contribute. For instance, for
![]() $\ell =d+1$
the only contributing terms are the ones corresponding to the partitions
$\ell =d+1$
the only contributing terms are the ones corresponding to the partitions
Similarly, we define
![]() $M_i'$
with
$M_i'$
with
![]() $\chi $
replaced by
$\chi $
replaced by
![]() $\chi '$
. Let
$\chi '$
. Let
![]() $A, B$
be the invertible linear maps
$A, B$
be the invertible linear maps

They are implemented in the Mathematica file as AutA and AutB, respectively. By considering the standard basis for
![]() $T^2, T^{d-2}$
we identify again
$T^2, T^{d-2}$
we identify again
![]() $A, B$
with
$A, B$
with
![]() $3\times 3$
matrices. More concretely,
$3\times 3$
matrices. More concretely,
![]() $A=(a_{st})_{0\leq s,\,t\leq 2}, B=(b_{st})_{0\leq s,\,t\leq 2}$
, where
$A=(a_{st})_{0\leq s,\,t\leq 2}, B=(b_{st})_{0\leq s,\,t\leq 2}$
, where
 $$ \begin{align*} \phi\big(c_{d-1-s}(s)\big)&=\sum_{t=0}^2 a_{st}c_{d-1-t}(t)+ \text{(lower terms in }\mathbb{C}[T]^{d-2})\,,\\ \phi\big(c_{3-s}(s)\big)&=\sum_{t=0}^2 b_{st}c_{3-t}(t)+ \text{(lower terms in }\mathbb{C}[T]^{2})\,. \end{align*} $$
$$ \begin{align*} \phi\big(c_{d-1-s}(s)\big)&=\sum_{t=0}^2 a_{st}c_{d-1-t}(t)+ \text{(lower terms in }\mathbb{C}[T]^{d-2})\,,\\ \phi\big(c_{3-s}(s)\big)&=\sum_{t=0}^2 b_{st}c_{3-t}(t)+ \text{(lower terms in }\mathbb{C}[T]^{2})\,. \end{align*} $$
Then the truncation of Equation (3.1) to
![]() $T^2\otimes T^{d-2}$
can be written as an equality between
$T^2\otimes T^{d-2}$
can be written as an equality between
![]() $3\times 3$
matrices
$3\times 3$
matrices
 $$ \begin{align} A^{\mathsf{T}} M_i B=\sum_{j=1}^3 s_{ij} M_j'\,,\quad i=1,2,3\,. \end{align} $$
$$ \begin{align} A^{\mathsf{T}} M_i B=\sum_{j=1}^3 s_{ij} M_j'\,,\quad i=1,2,3\,. \end{align} $$
Step 2: finding
 $s_{ij}$
$s_{ij}$
We begin with solving
![]() $s_{ij}$
for which there are matrices
$s_{ij}$
for which there are matrices
![]() $A, B$
satisfying Equation (3.2). By scaling both
$A, B$
satisfying Equation (3.2). By scaling both
![]() $A, B$
(hence also S), we may assume that
$A, B$
(hence also S), we may assume that
![]() $\det (A)=\det (B)=1$
. Then taking a linear combination of Equation (3.2) and applying the determinant it follows that
$\det (A)=\det (B)=1$
. Then taking a linear combination of Equation (3.2) and applying the determinant it follows that
 $$ \begin{align} \det\left(\sum_{i=1}^3x_i M_i\right)=\det\left(\sum_{i,j=1}^3 x_i s_{ij} M_j'\right)\,,\end{align} $$
$$ \begin{align} \det\left(\sum_{i=1}^3x_i M_i\right)=\det\left(\sum_{i,j=1}^3 x_i s_{ij} M_j'\right)\,,\end{align} $$
as an equality between two homogeneous cubic polynomials in
![]() $x_1, x_2, x_3$
. We let
$x_1, x_2, x_3$
. We let
![]() $E\subseteq {\mathbb {P}}^2$
be the cubic curve defined by
$E\subseteq {\mathbb {P}}^2$
be the cubic curve defined by
 $$\begin{align*}E=\left\{[x_1: x_2:x_3]\colon \det\left(\sum_{i=1}^3x_i M_i\right)\right\}\subseteq {\mathbb{P}}^2_{x_1, x_2, x_3}\,.\end{align*}$$
$$\begin{align*}E=\left\{[x_1: x_2:x_3]\colon \det\left(\sum_{i=1}^3x_i M_i\right)\right\}\subseteq {\mathbb{P}}^2_{x_1, x_2, x_3}\,.\end{align*}$$
Similarly, define
![]() $E'\subseteq {\mathbb {P}}^2$
. The matrix S defines an automorphism of
$E'\subseteq {\mathbb {P}}^2$
. The matrix S defines an automorphism of
![]() ${\mathbb {P}}^2_{x_1, x_2, x_3}$
sending E to
${\mathbb {P}}^2_{x_1, x_2, x_3}$
sending E to
![]() $E'$
.
$E'$
.
Lemma 3.3. The cubic curves
![]() $E, E'$
are elliptic nodal curves with a single node at
$E, E'$
are elliptic nodal curves with a single node at
![]() $[0:0:1]$
. Hence,
$[0:0:1]$
. Hence,
![]() $s_{31}=s_{32}=0$
.
$s_{31}=s_{32}=0$
.
Proof. We can directly compute the equation defining E. In the chart
the cubic polynomial defining E has the form
It follows that
![]() $[0:0:1]$
is indeed a node and the two branches of E at
$[0:0:1]$
is indeed a node and the two branches of E at
![]() $[0:0:1]$
are tangent to the lines
$[0:0:1]$
are tangent to the lines
![]() $x_1=0$
and
$x_1=0$
and
![]() $x_2=0$
. A cubic with a node either has exactly one node or has two nodes and is the union of a line and a conic. If the latter were the case, the line would necessarily be
$x_2=0$
. A cubic with a node either has exactly one node or has two nodes and is the union of a line and a conic. If the latter were the case, the line would necessarily be
![]() $x_1=0$
or
$x_1=0$
or
![]() $x_2=0$
, but this is not possible since
$x_2=0$
, but this is not possible since
![]() $\det (M_2)\neq 0$
and
$\det (M_2)\neq 0$
and
![]() $\det (M_1)\neq 0$
.
$\det (M_1)\neq 0$
.
Finally, we note that an automorphism of
![]() ${\mathbb {P}}^2_{x_1, x_2, x_3}$
sending E to
${\mathbb {P}}^2_{x_1, x_2, x_3}$
sending E to
![]() $E'$
must preserve the common node
$E'$
must preserve the common node
![]() $[0:0:1]$
, so it follows that
$[0:0:1]$
, so it follows that
![]() $s_{31}=s_{32}=0$
.
$s_{31}=s_{32}=0$
.
We now use Equation (3.3) to determine the remaining entries of S. Given a triple
![]() $(u,v,w)$
of nonnegative integers such that
$(u,v,w)$
of nonnegative integers such that
![]() $u+v+w=3$
, we get an equation among the entries of S by comparing the
$u+v+w=3$
, we get an equation among the entries of S by comparing the
![]() $x_1^ux_2^vx_3^w$
coefficient of both sides of Equation (3.3); this is implemented in the Mathematica file as coeff[u,v,w].Footnote
7
The triples
$x_1^ux_2^vx_3^w$
coefficient of both sides of Equation (3.3); this is implemented in the Mathematica file as coeff[u,v,w].Footnote
7
The triples
![]() $(0,2,1)$
and
$(0,2,1)$
and
![]() $(2,0,1)$
give, respectively,
$(2,0,1)$
give, respectively,
On the other hand, the equation for
![]() $(1,1,1)$
implies that
$(1,1,1)$
implies that
![]() $s_{33}\neq 0$
and
$s_{33}\neq 0$
and
![]() $s_{12}s_{21}+s_{11}s_{22}\neq 0$
. It follows that solutions must have either:
$s_{12}s_{21}+s_{11}s_{22}\neq 0$
. It follows that solutions must have either:
-
I.
 $s_{11}=s_{22}=0$
. We call the solutions of this form Type I solutions.
$s_{11}=s_{22}=0$
. We call the solutions of this form Type I solutions. -
II.
 $s_{12}=s_{21}=0$
. We call the solutions of this form Type II solutions.
$s_{12}=s_{21}=0$
. We call the solutions of this form Type II solutions.
From now on, we divide the analysis of Equations (3.2) and (3.3) according to the type of the solutions.
3.1. Type I
Suppose that S is a solution of Type I to Equation (3.3) so that we have already the vanishing of the entries
![]() $s_{31}=s_{32}=s_{11}=s_{22}=0$
. We now obtain the remaining entries. By looking at the
$s_{31}=s_{32}=s_{11}=s_{22}=0$
. We now obtain the remaining entries. By looking at the
![]() $(0,3,0)$
and
$(0,3,0)$
and
![]() $(3,0,0)$
equations, we obtain
$(3,0,0)$
equations, we obtain
![]() $s_{21}, s_{12}$
up to a choice of a cubic root of unity:
$s_{21}, s_{12}$
up to a choice of a cubic root of unity:
 $$ \begin{align*} s_{21}^3&=-d^3\frac{2 \chi (d-\chi) (d-2\chi) (d^2+8 d -16)}{ \chi^{\prime2} (d-\chi^{\prime})^2 (d-2\chi^{\prime})^{2} (d-2)}\,,\\ s_{12}^3&=-\frac{1}{d^3}\frac{ \chi^2 (d-\chi)^2 (d-2\chi)^2 (d-2)}{2 \chi^{\prime} (d-\chi^{\prime}) (d-2\chi^{\prime}) (d^2+8 d -16)}\,. \end{align*} $$
$$ \begin{align*} s_{21}^3&=-d^3\frac{2 \chi (d-\chi) (d-2\chi) (d^2+8 d -16)}{ \chi^{\prime2} (d-\chi^{\prime})^2 (d-2\chi^{\prime})^{2} (d-2)}\,,\\ s_{12}^3&=-\frac{1}{d^3}\frac{ \chi^2 (d-\chi)^2 (d-2\chi)^2 (d-2)}{2 \chi^{\prime} (d-\chi^{\prime}) (d-2\chi^{\prime}) (d^2+8 d -16)}\,. \end{align*} $$
Equation
![]() $(1,1,1)$
then writes
$(1,1,1)$
then writes
![]() $s_{33}$
in terms of
$s_{33}$
in terms of
![]() $s_{12}$
and
$s_{12}$
and
![]() $s_{21}$
and we can conclude that
$s_{21}$
and we can conclude that
![]() $s_{33}^3=1$
. By simultaneously scaling the matrices B and S, if necessary, by a cubic root of unityFootnote
8
we may assume without loss of generality that
$s_{33}^3=1$
. By simultaneously scaling the matrices B and S, if necessary, by a cubic root of unityFootnote
8
we may assume without loss of generality that
![]() $s_{33}=1$
. Finally, we obtain
$s_{33}=1$
. Finally, we obtain
![]() $s_{23}$
using
$s_{23}$
using
![]() $(1,2,0)$
and
$(1,2,0)$
and
![]() $s_{13}$
using
$s_{13}$
using
![]() $(2,1,0)$
; note that these are uniquely determined once we choose which cubic root we take for
$(2,1,0)$
; note that these are uniquely determined once we choose which cubic root we take for
![]() $s_{21}$
.
$s_{21}$
.
After having obtained S, the next step now is to solve Equation (3.2) for the entries of A and B. The equation is quadratic in the entries of A and B; however, by rewriting it as
 $$ \begin{align} A^{\mathsf{T}} M_i =\left(\sum_{j=1}^3 s_{ij} M_j'\right) B^{-1}\,,\quad i=1,2,3\,, \end{align} $$
$$ \begin{align} A^{\mathsf{T}} M_i =\left(\sum_{j=1}^3 s_{ij} M_j'\right) B^{-1}\,,\quad i=1,2,3\,, \end{align} $$
it becomes a linear (homogeneous) system in the entries
![]() $a_{st}$
of A and in the entries
$a_{st}$
of A and in the entries
![]() $\tilde b_{st}$
(written as bb[s,t] in the Mathematica file) of
$\tilde b_{st}$
(written as bb[s,t] in the Mathematica file) of
![]() $B^{-1}$
. It turns out that the linear system only admits the trivial solution
$B^{-1}$
. It turns out that the linear system only admits the trivial solution
![]() $a_{st}=\tilde b_{st}=0$
. Indeed, we can express all
$a_{st}=\tilde b_{st}=0$
. Indeed, we can express all
![]() $a_{st}, \tilde {b}_{st}$
as a multiple of
$a_{st}, \tilde {b}_{st}$
as a multiple of
![]() $a_{33}$
, and one additional constraint, denoted by Diff[d,chi1,chi2][[1]][[1,2]] in the Mathematica file, imposes that
$a_{33}$
, and one additional constraint, denoted by Diff[d,chi1,chi2][[1]][[1,2]] in the Mathematica file, imposes that
 $$\begin{align*}-\frac{2 \chi (d-4) (d-\chi)(d-2\chi) a_{33}}{d ((d-2) d^2+ 24 d{\chi'}-24 {\chi'}^2)}=0, \end{align*}$$
$$\begin{align*}-\frac{2 \chi (d-4) (d-\chi)(d-2\chi) a_{33}}{d ((d-2) d^2+ 24 d{\chi'}-24 {\chi'}^2)}=0, \end{align*}$$
whence
![]() $a_{33}=0$
. Note that the denominator is always positive, thus nonzero. This gives a contradiction since A and B are invertible matrices; thus, there are no solutions to Equation (3.1) with S of Type I.
$a_{33}=0$
. Note that the denominator is always positive, thus nonzero. This gives a contradiction since A and B are invertible matrices; thus, there are no solutions to Equation (3.1) with S of Type I.
3.2. Type II
Suppose that S is a solution of Type II to Equation (3.3). We already have the vanishing of the entries
![]() $s_{31}=s_{32}=s_{12}=s_{21}=0$
. The remaining entries are obtained exactly as in the Type I case. The equations
$s_{31}=s_{32}=s_{12}=s_{21}=0$
. The remaining entries are obtained exactly as in the Type I case. The equations
![]() $(3,0,0)$
and
$(3,0,0)$
and
![]() $(0,3,0)$
determine, respectively,
$(0,3,0)$
determine, respectively,
![]() $s_{11}$
and
$s_{11}$
and
![]() $s_{22}$
up to a choice of a cubic root:
$s_{22}$
up to a choice of a cubic root:
 $$\begin{align*}s_{11}^3=\left(\frac{\chi(d-\chi)(d-2\chi)}{\chi'(d-\chi')(d-2\chi')}\right)^2\,,\quad s_{22}^3=\frac{\chi(d-\chi)(d-2\chi)}{\chi'(d-\chi')(d-2\chi')}\,.\end{align*}$$
$$\begin{align*}s_{11}^3=\left(\frac{\chi(d-\chi)(d-2\chi)}{\chi'(d-\chi')(d-2\chi')}\right)^2\,,\quad s_{22}^3=\frac{\chi(d-\chi)(d-2\chi)}{\chi'(d-\chi')(d-2\chi')}\,.\end{align*}$$
Equation
![]() $(1,1,1)$
then writes
$(1,1,1)$
then writes
![]() $s_{33}$
in terms of
$s_{33}$
in terms of
![]() $s_{11}$
and
$s_{11}$
and
![]() $s_{22}$
and we can conclude that
$s_{22}$
and we can conclude that
![]() $s_{33}^3=1$
. As we did for Type I, we may assume without loss of generality that
$s_{33}^3=1$
. As we did for Type I, we may assume without loss of generality that
![]() $s_{33}=1$
. This fixes
$s_{33}=1$
. This fixes
![]() $s_{11}=s_{22}^2$
. Finally, we obtain
$s_{11}=s_{22}^2$
. Finally, we obtain
![]() $s_{13}$
using
$s_{13}$
using
![]() $(2,1,0)$
and
$(2,1,0)$
and
![]() $s_{23}$
using
$s_{23}$
using
![]() $(1,2,0)$
; note that these are uniquely determined once we choose which cubic root we take for
$(1,2,0)$
; note that these are uniquely determined once we choose which cubic root we take for
![]() $s_{22}$
.
$s_{22}$
.
After obtaining S, Equation (3.4) is again linear in the entries
![]() $a_{st}$
of A and in the entries
$a_{st}$
of A and in the entries
![]() $\tilde b_{st}$
of
$\tilde b_{st}$
of
![]() $B^{-1}$
. The linear system can be solved explicitly, and it turns out that it has a one-dimensional space of solutions. By writing all the variables in terms of
$B^{-1}$
. The linear system can be solved explicitly, and it turns out that it has a one-dimensional space of solutions. By writing all the variables in terms of
![]() $a_{11}$
, the normalization imposed on the determinant
$a_{11}$
, the normalization imposed on the determinant
![]() $\det (A)=1$
gives
$\det (A)=1$
gives
By further scaling A by a cubic root of unity and scaling B by its inverse hence leaving S unchanged, we may assume without loss of generality that
![]() $a_{11}=s_{22}$
. This completely solves all the matrices
$a_{11}=s_{22}$
. This completely solves all the matrices
![]() $S, A, B$
once we choose which cubic root we take for
$S, A, B$
once we choose which cubic root we take for
![]() $s_{11}$
. Solutions are implemented in the Mathematica file as solS[d,chi1,chi2], solA[d,chi1,chi2], solB[d,chi1,chi2], respectively.
$s_{11}$
. Solutions are implemented in the Mathematica file as solS[d,chi1,chi2], solA[d,chi1,chi2], solB[d,chi1,chi2], respectively.
Remark 3.4. When
![]() $\chi =\chi '$
, the unique solution of Type II is given by
$\chi =\chi '$
, the unique solution of Type II is given by
![]() $S=A=B=\text {Id}_{3\times 3}$
, as expected. When
$S=A=B=\text {Id}_{3\times 3}$
, as expected. When
![]() $\chi +\chi '=d$
, the solution is given by simple sign matrices
$\chi +\chi '=d$
, the solution is given by simple sign matrices
 $$ \begin{align*}A=B=\begin{bmatrix}-1& 0& 0\\ 0& 1&0\\ 0&0&-1\end{bmatrix},\quad S=\begin{bmatrix}1& 0& 0\\ 0& -1& 0\\ 0&0&1\end{bmatrix}. \end{align*} $$
$$ \begin{align*}A=B=\begin{bmatrix}-1& 0& 0\\ 0& 1&0\\ 0&0&-1\end{bmatrix},\quad S=\begin{bmatrix}1& 0& 0\\ 0& -1& 0\\ 0&0&1\end{bmatrix}. \end{align*} $$
In either case, these truncated solutions extend to a solution of Equation (3.1) since the moduli spaces
![]() $M_{d, \chi }$
and
$M_{d, \chi }$
and
![]() $M_{d, \chi '}$
are isomorphic. Indeed, the solution matrices are compatible with Proposition 2.1(c) which describes how the tautological generators are mapped under the two types of symmetries.
$M_{d, \chi '}$
are isomorphic. Indeed, the solution matrices are compatible with Proposition 2.1(c) which describes how the tautological generators are mapped under the two types of symmetries.
3.3. Type II – extended matrices
Recall that we have used only a part of the full Equation (3.1) truncated via the projection
![]() ${\mathbb {C}}[T]^d\twoheadrightarrow T^2\otimes T^{d-2}$
. This was sufficient to determine
${\mathbb {C}}[T]^d\twoheadrightarrow T^2\otimes T^{d-2}$
. This was sufficient to determine
![]() $A, B$
and S.
$A, B$
and S.
Step 3: bigger truncation
We proceed by considering a bigger truncation via the projection
We can regard the truncated relations as a block
![]() $3\times (3\mid 3)$
matrix by identifying
$3\times (3\mid 3)$
matrix by identifying
where
![]() $M_i$
is as before and
$M_i$
is as before and
![]() $N_i$
is implemented in the Mathematica file as ExtRelations[d,chi]. Similarly, we define
$N_i$
is implemented in the Mathematica file as ExtRelations[d,chi]. Similarly, we define
![]() $\begin {bmatrix}M_i'&N_i'\end {bmatrix}$
with
$\begin {bmatrix}M_i'&N_i'\end {bmatrix}$
with
![]() $\chi $
replaced by
$\chi $
replaced by
![]() $\chi '$
. As before,
$\chi '$
. As before,
![]() $\phi $
induces a linear map
$\phi $
induces a linear map

where
![]() $U:T^2\rightarrow {\text {Sym}}^2(T^1)$
and
$U:T^2\rightarrow {\text {Sym}}^2(T^1)$
and
![]() $V:{\text {Sym}}^2(T^1)\rightarrow {\text {Sym}}^2(T^1)$
. They are implemented in the Mathematica file as AutU and AutV, respectively. Note that the lower left block is zero because
$V:{\text {Sym}}^2(T^1)\rightarrow {\text {Sym}}^2(T^1)$
. They are implemented in the Mathematica file as AutU and AutV, respectively. Note that the lower left block is zero because
![]() $\phi $
is a graded ring isomorphism. Then the truncation of Equation (3.1) to
$\phi $
is a graded ring isomorphism. Then the truncation of Equation (3.1) to
![]() $\Big (T^2\oplus {\text {Sym}}^2(T^1)\Big )\otimes T^{d-2}$
can be written as an equality between
$\Big (T^2\oplus {\text {Sym}}^2(T^1)\Big )\otimes T^{d-2}$
can be written as an equality between
![]() $3\times 6$
matrices
$3\times 6$
matrices
 $$ \begin{align*} A^{\mathsf{T}} \begin{bmatrix}M_i&N_i\end{bmatrix} \begin{bmatrix}B& U\\ 0& V\\\end{bmatrix}=\sum_{j=1}^3 s_{ij} \begin{bmatrix}M_j'&N_j'\end{bmatrix}\,,\quad i=1,2,3\,. \end{align*} $$
$$ \begin{align*} A^{\mathsf{T}} \begin{bmatrix}M_i&N_i\end{bmatrix} \begin{bmatrix}B& U\\ 0& V\\\end{bmatrix}=\sum_{j=1}^3 s_{ij} \begin{bmatrix}M_j'&N_j'\end{bmatrix}\,,\quad i=1,2,3\,. \end{align*} $$
Since
![]() $A, B$
and S satisfy Equation (3.2), this reduces to
$A, B$
and S satisfy Equation (3.2), this reduces to
 $$ \begin{align} A^{\mathsf{T}}M_iU+A^{\mathsf{T}}N_iV=\sum_{j=1}^3 s_{ij} N_j'\,,\quad i=1,2,3\,, \end{align} $$
$$ \begin{align} A^{\mathsf{T}}M_iU+A^{\mathsf{T}}N_iV=\sum_{j=1}^3 s_{ij} N_j'\,,\quad i=1,2,3\,, \end{align} $$
which is a linear system in the entries
![]() $u_{st}$
and
$u_{st}$
and
![]() $v_{st}$
of U and V, respectively.
$v_{st}$
of U and V, respectively.
We show that this linear system, referred to as ExtDiff[d,chi1,chi2] in the Mathematica file, has a solution only if
![]() $\chi =\chi '$
or
$\chi =\chi '$
or
![]() $\chi +\chi '=d$
. By using certain parts of the linear system (3.5), as explained in the Mathematica file, we can express
$\chi +\chi '=d$
. By using certain parts of the linear system (3.5), as explained in the Mathematica file, we can express
![]() $u_{11}, u_{21}, u_{31}, v_{11}, v_{21}$
in terms of
$u_{11}, u_{21}, u_{31}, v_{11}, v_{21}$
in terms of
![]() $v_{31}$
. Once this is done, we further use two of the remaining linear system (3.5), referred to as ExtDiff[d,chi1,chi2][[1]][[1,1]] and ExtDiff[d,chi1,chi2][[1]][[2,1]], which take the form
$v_{31}$
. Once this is done, we further use two of the remaining linear system (3.5), referred to as ExtDiff[d,chi1,chi2][[1]][[1,1]] and ExtDiff[d,chi1,chi2][[1]][[2,1]], which take the form
following the notations from the code. Existence of the solution
![]() $v_{31}$
implies an equation which is purely in terms of d,
$v_{31}$
implies an equation which is purely in terms of d,
![]() $\chi $
and
$\chi $
and
![]() $\chi '$
:
$\chi '$
:
This expression admits a factorization
with
![]() $\texttt {(other terms)}$
being clearly nonzero; see the Mathematica file. Note that the roles of
$\texttt {(other terms)}$
being clearly nonzero; see the Mathematica file. Note that the roles of
![]() $\chi $
and
$\chi $
and
![]() $\chi '$
are symmetric; we conclude that
$\chi '$
are symmetric; we conclude that
We are left to prove that Equation (3.6) implies
![]() $\chi =\chi '$
or
$\chi =\chi '$
or
![]() $\chi +\chi '=d$
. Suppose for the contradiction that
$\chi +\chi '=d$
. Suppose for the contradiction that
![]() $\chi \neq \chi '$
and
$\chi \neq \chi '$
and
![]() $\chi +\chi '\neq d$
.
$\chi +\chi '\neq d$
.
We first show that
![]() $P_2(d,\chi ,\chi ')$
and
$P_2(d,\chi ,\chi ')$
and
![]() $P_2(d,\chi ',\chi )$
are nonzero. From the formula in the file, it is straightforward to check that
$P_2(d,\chi ',\chi )$
are nonzero. From the formula in the file, it is straightforward to check that
![]() $P_2(d,\chi ,\chi ')=0$
if and only if
$P_2(d,\chi ,\chi ')=0$
if and only if
![]() $P_2(d,\chi ',\chi )=0$
, if and only if
$P_2(d,\chi ',\chi )=0$
, if and only if
for some explicit integral polynomial
![]() $f(d,\chi ,\chi ')$
. Since we assumed that
$f(d,\chi ,\chi ')$
. Since we assumed that
![]() $\chi \neq \chi '$
and
$\chi \neq \chi '$
and
![]() $\chi +\chi '\neq d$
, the last term must vanish. On the other hand,
$\chi +\chi '\neq d$
, the last term must vanish. On the other hand,
![]() $\gcd (d,\chi )=\gcd (d,\chi ')=1$
implies that d must divide
$\gcd (d,\chi )=\gcd (d,\chi ')=1$
implies that d must divide
![]() $216$
. This further implies that
$216$
. This further implies that
![]() $d^2$
divides
$d^2$
divides
![]() $216$
by looking at the linear term in d, so we are left with
$216$
by looking at the linear term in d, so we are left with
![]() $d=1,2,3,6$
. But there are no nontrivial pairs
$d=1,2,3,6$
. But there are no nontrivial pairs
![]() $\chi $
and
$\chi $
and
![]() $\chi '$
for such d.
$\chi '$
for such d.
Therefore, we may assume
![]() $P_1(d,\chi )=P_1(d,\chi ')=0$
. We can check that
$P_1(d,\chi )=P_1(d,\chi ')=0$
. We can check that
![]() $P_1(d,x)$
is a degree four polynomial in x, with the symmetry
$P_1(d,x)$
is a degree four polynomial in x, with the symmetry
This implies that
![]() $P_1(d,x)$
is a degree four polynomial with four distinct roots
$P_1(d,x)$
is a degree four polynomial with four distinct roots
all within the interval
![]() $[1,d-1]$
. On the other hand, explicit computation shows that
$[1,d-1]$
. On the other hand, explicit computation shows that
as long as
![]() $d\geq 5$
. This forces
$d\geq 5$
. This forces
![]() $P_1(d,x)$
to have an additional root in the interval
$P_1(d,x)$
to have an additional root in the interval
![]() $(0,1)$
, which contradicts that it is a degree four polynomial. It follows that Equation (3.6) implies
$(0,1)$
, which contradicts that it is a degree four polynomial. It follows that Equation (3.6) implies
![]() $\chi =\chi '$
or
$\chi =\chi '$
or
![]() $\chi +\chi '=d$
, hence completing the proof.
$\chi +\chi '=d$
, hence completing the proof.
Acknowledgements
We thank Yakov Kononov for his help on coding and for numerous helpful conversations. The third author wishes to thank Rahul Pandharipande for inviting him to visit ETH Zürich, which eventually resulted in this collaboration, and thanks to Junliang Shen, his academic advisor, for proposing this interesting problem in the first place.
Funding statement
The first author is supported by the grant SNF-200020-182181. The second author is supported by ERC-2017-AdG-786580-MACI. The project received funding from the European Research Council (ERC) under the European Union Horizon 2020 research and innovation programme (grant agreement 786580).
Competing interest
The authors have no competing interest to declare.
Data availability statement
The code used in this article (together with a printed file of the output) has been uploaded to the third author’s website https://github.com/Weite-Pi/weitepi.github.io under the name cohomological ring chi-dependence.
Ethical standards
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.