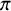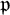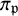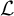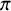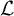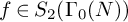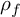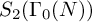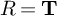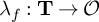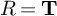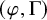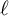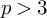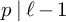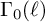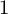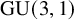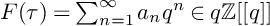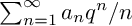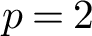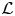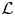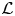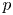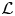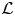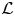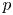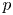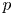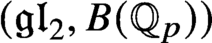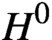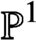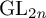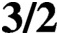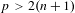71 results
L-invariants for cohomological representations of PGL(2) over arbitrary number fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 30 May 2024, e71
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
WILES DEFECT OF HECKE ALGEBRAS VIA LOCAL-GLOBAL ARGUMENTS: WITH AN APPENDIX BY NAJMUDDIN FAKHRUDDIN AND CHANDRASHEKHAR B. KHARE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 25 April 2024, pp. 1-81
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modularity of trianguline Galois representations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 05 January 2024, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Eisenstein congruences among Euler systems
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 425-446
- Print publication:
- June 2024
-
- Article
- Export citation
THE EISENSTEIN IDEAL OF WEIGHT k AND RANKS OF HECKE ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 31 March 2023, pp. 983-1017
- Print publication:
- March 2024
-
- Article
- Export citation
Iwasawa–Greenberg main conjecture for nonordinary modular forms and Eisenstein congruences on GU(3,1)
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 15 December 2022, e110
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MAGNETIC (QUASI-)MODULAR FORMS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 30 May 2022, pp. 849-864
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON A PROPERNESS OF THE HILBERT EIGENVARIETY AT INTEGRAL WEIGHTS: THE CASE OF QUADRATIC RESIDUE FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 08 April 2022, pp. 2645-2716
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE p-ADIC GROSS–ZAGIER FORMULA ON SHIMURA CURVES, II: NONSPLIT PRIMES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 15 February 2022, pp. 2199-2240
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Big principal series,
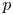 $p$-adic families and
$p$-adic families and 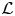 $\mathcal {L}$-invariants
$\mathcal {L}$-invariants
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 25 April 2022, pp. 409-436
- Print publication:
- February 2022
-
- Article
- Export citation
The spectral p-adic Jacquet–Langlands correspondence and a question of Serre
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 11 April 2022, pp. 245-286
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GEOMETRIC WEIGHT-SHIFTING OPERATORS ON HILBERT MODULAR FORMS IN CHARACTERISTIC p
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 15 November 2021, pp. 1871-1930
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONGRUENCES OF SAITO–KUROKAWA LIFTS AND DENOMINATORS OF CENTRAL SPINOR L-VALUES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 14 October 2021, pp. 504-525
- Print publication:
- May 2022
-
- Article
- Export citation
Overconvergent modular forms are highest-weight vectors in the Hodge-Tate weight zero part of completed cohomology
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 02 March 2021, e17
-
- Article
-
- You have access
- Open access
- Export citation
RAISING THE LEVEL OF AUTOMORPHIC REPRESENTATIONS OF
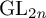 $\mathrm {GL}_{2n}$
OF UNITARY TYPE
$\mathrm {GL}_{2n}$
OF UNITARY TYPE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 09 February 2021, pp. 1421-1444
- Print publication:
- July 2022
-
- Article
-
- You have access
- Open access
- Export citation
Vanishing theorems for the mod p cohomology of some simple Shimura varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 03 November 2020, e38
-
- Article
-
- You have access
- Open access
- Export citation
CONGRUENCES MODULO 4 FOR WEIGHT
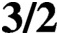 $\textbf{3/2}$
ETA-PRODUCTS
$\textbf{3/2}$
ETA-PRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 405-417
- Print publication:
- June 2021
-
- Article
- Export citation
CONGRUENCE PRIMES FOR SIEGEL MODULAR FORMS OF PARAMODULAR LEVEL AND APPLICATIONS TO THE BLOCH–KATO CONJECTURE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 29 September 2020, pp. 660-681
- Print publication:
- September 2021
-
- Article
- Export citation
GLOBALLY REALIZABLE COMPONENTS OF LOCAL DEFORMATION RINGS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 03 September 2020, pp. 533-602
- Print publication:
- March 2022
-
- Article
- Export citation
A
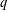 $q$-ANALOGUE OF A DWORK-TYPE SUPERCONGRUENCE
$q$-ANALOGUE OF A DWORK-TYPE SUPERCONGRUENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 17 July 2020, pp. 303-310
- Print publication:
- April 2021
-
- Article
- Export citation