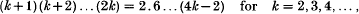36 results
Contributions towards a conjecture of Erdős on perfect powers in arithmetic progression
-
- Journal:
- Compositio Mathematica / Volume 141 / Issue 3 / May 2005
- Published online by Cambridge University Press:
- 21 April 2005, pp. 541-560
- Print publication:
- May 2005
-
- Article
-
- You have access
- Export citation
Almost Squares and Factorisations in Consecutive Integers
-
- Journal:
- Compositio Mathematica / Volume 138 / Issue 1 / August 2003
- Published online by Cambridge University Press:
- 04 December 2007, pp. 113-124
- Print publication:
- August 2003
-
- Article
-
- You have access
- Export citation
Almost Squares in Arithmetic Progression
-
- Journal:
- Compositio Mathematica / Volume 138 / Issue 1 / August 2003
- Published online by Cambridge University Press:
- 04 December 2007, pp. 73-111
- Print publication:
- August 2003
-
- Article
-
- You have access
- Export citation
20 - Powers in Arithmetic Progression
-
-
- Book:
- A Panorama of Number Theory <I>or</I> The View from Baker's Garden
- Published online:
- 20 August 2009
- Print publication:
- 26 September 2002, pp 325-336
-
- Chapter
- Export citation
DIOPHANTINE APPROXIMATION ON LINEAR ALGEBRAIC GROUPS: TRANSCENDENCE PROPERTIES OF THE EXPONENTIAL FUNCTION IN SEVERAL VARIABLES (Grundlehren der Mathematischen Wissenschaften 326) By MICHEL WALDSCHMIDT: 633 pp., $58.50, ISBN 3-540-66785-7 (Springer, Berlin, 2000).
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 34 / Issue 1 / January 2002
- Published online by Cambridge University Press:
- 18 January 2002, pp. 108-119
- Print publication:
- January 2002
-
- Article
- Export citation
The equation formula here has no solution with x square
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 127 / Issue 3 / November 1999
- Published online by Cambridge University Press:
- 01 November 1999, pp. 353-372
- Print publication:
- November 1999
-
- Article
- Export citation
The equation xn−1/x−1= yq with x square
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 125 / Issue 1 / January 1999
- Published online by Cambridge University Press:
- 01 January 1999, pp. 1-19
- Print publication:
- January 1999
-
- Article
- Export citation
On arithmetic progressions of equal lengths with equal products
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 117 / Issue 2 / March 1995
- Published online by Cambridge University Press:
- 24 October 2008, pp. 193-201
- Print publication:
- March 1995
-
- Article
- Export citation
On the greatest prime factor of an arithmetical progression
-
-
- Book:
- A Tribute to Paul Erdos
- Published online:
- 05 March 2012
- Print publication:
- 13 December 1990, pp 385-390
-
- Chapter
- Export citation
22 - Some exponential Diophantine equations
-
-
- Book:
- New Advances in Transcendence Theory
- Published online:
- 05 January 2012
- Print publication:
- 13 October 1988, pp 352-365
-
- Chapter
- Export citation
Preface
-
- Book:
- Exponential Diophantine Equations
- Published online:
- 04 May 2010
- Print publication:
- 27 November 1986, pp ix-x
-
- Chapter
- Export citation
1 - Purely exponential equations
-
- Book:
- Exponential Diophantine Equations
- Published online:
- 04 May 2010
- Print publication:
- 27 November 1986, pp 40-55
-
- Chapter
- Export citation
B - Estimates of linear forms in logarithms
-
- Book:
- Exponential Diophantine Equations
- Published online:
- 04 May 2010
- Print publication:
- 27 November 1986, pp 29-31
-
- Chapter
- Export citation
5 - The Thue equation
-
- Book:
- Exponential Diophantine Equations
- Published online:
- 04 May 2010
- Print publication:
- 27 November 1986, pp 99-112
-
- Chapter
- Export citation
12 - The Catalan equation and related equations
-
- Book:
- Exponential Diophantine Equations
- Published online:
- 04 May 2010
- Print publication:
- 27 November 1986, pp 201-220
-
- Chapter
- Export citation
Notation
-
- Book:
- Exponential Diophantine Equations
- Published online:
- 04 May 2010
- Print publication:
- 27 November 1986, pp 5-8
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Exponential Diophantine Equations
- Published online:
- 04 May 2010
- Print publication:
- 27 November 1986, pp i-vi
-
- Chapter
- Export citation
6 - The superelliptic equation
-
- Book:
- Exponential Diophantine Equations
- Published online:
- 04 May 2010
- Print publication:
- 27 November 1986, pp 113-123
-
- Chapter
- Export citation
References
-
- Book:
- Exponential Diophantine Equations
- Published online:
- 04 May 2010
- Print publication:
- 27 November 1986, pp 221-238
-
- Chapter
- Export citation

Exponential Diophantine Equations
-
- Published online:
- 04 May 2010
- Print publication:
- 27 November 1986