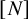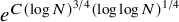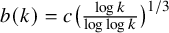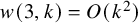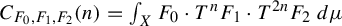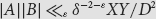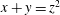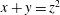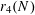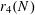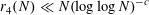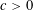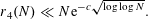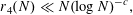34 results
New lower bounds for van der Waerden numbers
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 13 July 2022, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multiple correlation sequences not approximable by nilsequences
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 16 July 2021, pp. 2711-2722
- Print publication:
- September 2022
-
- Article
- Export citation
Extremal problems for GCDs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 08 April 2021, pp. 922-929
-
- Article
-
- You have access
- Open access
- Export citation
Monochromatic Solutions to
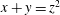 $x+y=z^{2}$
$x+y=z^{2}$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 579-605
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
A note on multiplicative functions on progressions to large moduli
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 December 2017, pp. 63-77
- Print publication:
- February 2018
-
- Article
- Export citation
Having the sceptre: Wu-Tang Clan and the aura of music in the age of digital reproduction
-
- Journal:
- Popular Music / Volume 36 / Issue 3 / October 2017
- Published online by Cambridge University Press:
- 09 October 2017, pp. 427-440
- Print publication:
- October 2017
-
- Article
- Export citation
NEW BOUNDS FOR SZEMERÉDI’S THEOREM, III: A POLYLOGARITHMIC BOUND FOR
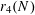 $r_{4}(N)$
$r_{4}(N)$
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 944-1040
- Print publication:
- 2017
-
- Article
-
- You have access
- HTML
- Export citation
On the Chromatic Number of Random Cayley Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 2 / March 2017
- Published online by Cambridge University Press:
- 09 September 2016, pp. 248-266
-
- Article
- Export citation
Emmanuel Breuillard and Hee Oh, Thin groups and superstrong approximation (Cambridge University Press, 2014), 376 pp., 978-1-107-03685-7 (hardback), £65.
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 21 June 2016, pp. 811-812
-
- Article
- Export citation
Contributors
-
-
- Book:
- Clinical Gynecology
- Published online:
- 05 April 2015
- Print publication:
- 23 April 2015, pp viii-xiv
-
- Chapter
- Export citation
Contributors
-
-
- Book:
- Organising Music
- Published online:
- 05 January 2015
- Print publication:
- 05 February 2015, pp xii-xxviii
-
- Chapter
- Export citation
Contributors
-
-
- Book:
- The Burdens of Mental Disorders
- Print publication:
- 09 May 2013, pp ix-xii
-
- Chapter
- Export citation
Post-traumatic stress disorder: new directions in pharmacotherapy
-
- Journal:
- Advances in Psychiatric Treatment / Volume 19 / Issue 3 / May 2013
- Published online by Cambridge University Press:
- 02 January 2018, pp. 181-190
- Print publication:
- May 2013
-
- Article
-
- You have access
- HTML
- Export citation
GASKAP—The Galactic ASKAP Survey
- Part of
-
- Journal:
- Publications of the Astronomical Society of Australia / Volume 30 / 2013
- Published online by Cambridge University Press:
- 24 January 2013, e003
-
- Article
-
- You have access
- HTML
- Export citation
On (Not) Computing the Möbius Function Using Bounded Depth Circuits
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 24 August 2012, pp. 942-951
-
- Article
- Export citation
Adverse effects of psychotherapy
-
- Journal:
- Advances in Psychiatric Treatment / Volume 17 / Issue 6 / November 2011
- Published online by Cambridge University Press:
- 02 January 2018, p. 476
- Print publication:
- November 2011
-
- Article
-
- You have access
- HTML
- Export citation
Linked indicator sets for addressing biodiversity loss
-
- Article
-
- You have access
- HTML
- Export citation
AN INVERSE THEOREM FOR THE GOWERS U4-NORM
-
- Journal:
- Glasgow Mathematical Journal / Volume 53 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 25 August 2010, pp. 1-50
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
Approximate groups. I The torsion-free nilpotent case
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 10 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 02 June 2010, pp. 37-57
- Print publication:
- January 2011
-
- Article
- Export citation
An equivalence between inverse sumset theorems and inverse conjectures for the U3 norm
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 149 / Issue 1 / July 2010
- Published online by Cambridge University Press:
- 24 March 2010, pp. 1-19
- Print publication:
- July 2010
-
- Article
- Export citation