The Wigner 6j–symbol, written in the form
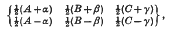
is shown to be invariant under separate permutations of A, B, C alone, separate permutations of α, β, γ alone and separate change in sign of any pair of α, β, γ; results equivalent to the new symmetry relations of Regge. Alternatively, written in the form
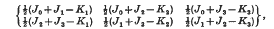
with J0 + J1 + J2 + J3 = K1 + K2 + K3, Jr(r = 0, 1, 2, 3) and K3 (s = 1, 2, 3) integral, it is invariant for separate permutations of the Jr and of the Ks. If Jm = max (J0, J1, J2, J3), then each 6j-symbol with distinct value may be associated with an ordered partition of Jm into 6 integral parts: Jm = n1 + n2 + n3 + p1 + p2 + p3, n1 ≥ n2 ≥ n3; p1 ≥ p2 ≥ n3. The 6j-symbol is proportional to the Saalschützian
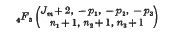
of unit argument.