Research Article
Two more representation problems
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 1-17
-
- Article
-
- You have access
- Export citation
Groups generated by elements with rational fixed points
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 19-30
-
- Article
-
- You have access
- Export citation
The Frattini p-subalgebra of a solvable Lie p-algebra
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 31-40
-
- Article
-
- You have access
- Export citation
Weighted spaces of harmonic and holomorphic functions: sequence space representations and protective descriptions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 41-62
-
- Article
-
- You have access
- Export citation
On joins with group congruences
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 63-67
-
- Article
-
- You have access
- Export citation
Classifications of 2-complexes whose finite fundamental group is that of a 3-manifold
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 69-84
-
- Article
-
- You have access
- Export citation
Space sextic curves with six bitangents, and some geometry of the diagonal cubic surface
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 85-97
-
- Article
-
- You have access
- Export citation
Modularity* in Lie algebras
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 99-110
-
- Article
-
- You have access
- Export citation
Effective computation of the Gelfand-Kirillov dimension*
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 111-117
-
- Article
-
- You have access
- Export citation
A note on function spaces generated by Rademacher series
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 119-126
-
- Article
-
- You have access
- Export citation
A time-like surface in Minkowski 3-space which contains pseudocircles
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 127-136
-
- Article
-
- You have access
- Export citation
A note on the Gaussian cardinal-interpolation operator
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 137-149
-
- Article
-
- You have access
- Export citation
The Bourgain algebra of a nest algebra
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 151-166
-
- Article
-
- You have access
- Export citation
Comments on some inequalities of Pearce and Pečarić
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 167-174
-
- Article
-
- You have access
- Export citation
Essentially defined derivations on semisimple Banach algebras
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 175-179
-
- Article
-
- You have access
- Export citation
Weakly compact multilinear mappings
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 181-192
-
- Article
-
- You have access
- Export citation
A note on weighted maximal inequalities
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 193-205
-
- Article
-
- You have access
- Export citation
Book Reviews
P. Borwein and T. Erd Lyi Polynomials and polynomial inequalities (Graduate Texts in Mathematics, Vol. 161, Springer-Verlag, Berlin-Heidelberg-New York-London-Paris-Tokyo-Hong Kong, 1995), x + 480 pp., hardcover 0 387 945091, DM 98.00.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 207
-
- Article
-
- You have access
- Export citation
P. J. Olver Equivalence, invariants, and symmetry (Cambridge University Press, Cambridge, 1995), xvi + 525 pp., 0 521 47811 1 (hardback), £24.95.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 208-209
-
- Article
-
- You have access
- Export citation
D. S. Mitrinović, J. Sándor and B. Crstici Handbook of Number Theory (Mathematics and its Applications Vol. 351, Kluwer Academic Publishers, Dordrecht, 1995), xxvi + 622 pp., 0 7923 3823 5, £179.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 209-210
-
- Article
-
- You have access
- Export citation

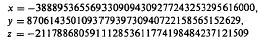
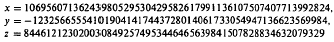
 be an arbitrary semigroup. A congruence γ on
be an arbitrary semigroup. A congruence γ on  (
(
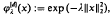 ,
, 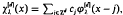 ,
, 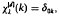 ,
, 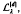 , given by
, given by 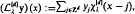 ,
, 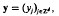 , is a well-defīned linear map from ℓ
, is a well-defīned linear map from ℓ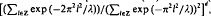 , implying, in particular, that
, implying, in particular, that 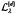 is contractive. Some sidelights are also presented.
is contractive. Some sidelights are also presented.