Research Article
Idempotent-generated semigroups and pseudovarieties
- Part of:
-
- Published online by Cambridge University Press:
- 20 June 2011, pp. 545-568
-
- Article
-
- You have access
- Export citation
The ρ-variation of the heat semigroup in the Hermitian setting: behaviour in L∞
- Part of:
-
- Published online by Cambridge University Press:
- 14 June 2011, pp. 569-585
-
- Article
-
- You have access
- Export citation
Bounds for the multiplicities of the roots of a complex polynomial
- Part of:
-
- Published online by Cambridge University Press:
- 08 April 2011, pp. 587-598
-
- Article
-
- You have access
- Export citation
On simultaneous rational approximation to a p-adic number and its integral powers
- Part of:
-
- Published online by Cambridge University Press:
- 17 August 2011, pp. 599-612
-
- Article
-
- You have access
- Export citation
The braided monoidal structures on the category of vector spaces graded by the Klein group
- Part of:
-
- Published online by Cambridge University Press:
- 14 June 2011, pp. 613-641
-
- Article
-
- You have access
- Export citation
Corrigendum: C*-envelopes of tensor algebras for multivariable dynamics
- Part of:
-
- Published online by Cambridge University Press:
- 20 May 2011, pp. 643-644
-
- Article
-
- You have access
- Export citation
Baire's category in existence problems for non-convex lower semicontinuous evolution differential inclusions
- Part of:
-
- Published online by Cambridge University Press:
- 15 June 2011, pp. 645-667
-
- Article
-
- You have access
- Export citation
Symmetric presentations of Coxeter groups
- Part of:
-
- Published online by Cambridge University Press:
- 20 June 2011, pp. 669-683
-
- Article
-
- You have access
- Export citation
Supremum and infimum of subharmonic functions of order between 1 and 2
- Part of:
-
- Published online by Cambridge University Press:
- 08 April 2011, pp. 685-693
-
- Article
-
- You have access
- Export citation
Alternating units as free factors in the group of units of integral group rings
- Part of:
-
- Published online by Cambridge University Press:
- 14 June 2011, pp. 695-709
-
- Article
-
- You have access
- Export citation
On the number of holomorphic mappings between Riemann surfaces of finite analytic type
- Part of:
-
- Published online by Cambridge University Press:
- 20 June 2011, pp. 711-730
-
- Article
-
- You have access
- Export citation
Retracts of trees and free left adequate semigroups
- Part of:
-
- Published online by Cambridge University Press:
- 17 August 2011, pp. 731-747
-
- Article
-
- You have access
- Export citation
A new class of restricted type spaces
- Part of:
-
- Published online by Cambridge University Press:
- 11 April 2011, pp. 749-759
-
- Article
-
- You have access
- Export citation
Hypercyclic and mixing operator semigroups
- Part of:
-
- Published online by Cambridge University Press:
- 27 June 2011, pp. 761-782
-
- Article
-
- You have access
- Export citation
Cotorsion pairs and model structures on Ch(R)
- Part of:
-
- Published online by Cambridge University Press:
- 17 August 2011, pp. 783-797
-
- Article
-
- You have access
- Export citation
Weakly s-supplementally embedded minimal subgroups of finite groups
- Part of:
-
- Published online by Cambridge University Press:
- 17 August 2011, pp. 799-807
-
- Article
-
- You have access
- Export citation



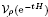 , ρ > 2, be the ρ-variation of the heat semigroup associated to the harmonic oscillator
, ρ > 2, be the ρ-variation of the heat semigroup associated to the harmonic oscillator 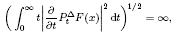
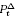 is the classical Poisson kernal in ℝ.
is the classical Poisson kernal in ℝ.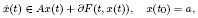
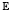 ,
, 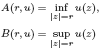
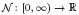 is a non-negative non-decreasing convex function of log
is a non-negative non-decreasing convex function of log 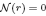 for all small
for all small 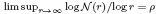 , where 1 < ρ < 2, and define
, where 1 < ρ < 2, and define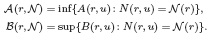
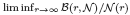 and a sharp lower bound is obtained for
and a sharp lower bound is obtained for 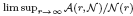 .
.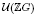 , the group of units of ℤ
, the group of units of ℤ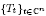 with holomorphic dependence on the parameter
with holomorphic dependence on the parameter 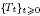 .
.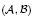 in the category of modules is complete and hereditary, then both of the induced cotorsion pairs in the category of complexes are complete. We also give a cofibrantly generated model structure that can be regarded as a generalization of the projective model structure.
in the category of modules is complete and hereditary, then both of the induced cotorsion pairs in the category of complexes are complete. We also give a cofibrantly generated model structure that can be regarded as a generalization of the projective model structure.