Hostname: page-component-76fb5796d-vfjqv Total loading time: 0 Render date: 2024-04-26T21:03:34.797Z Has data issue: false hasContentIssue false
  • English
  • Français

The ρ-variation of the heat semigroup in the Hermitian setting: behaviour in L∞

Part of: Nontrigonometric harmonic analysis

Published online by Cambridge University Press:  14 June 2011

J. J. Betancor ,
R. Crescimbeni  and
J. L. Torrea
J. J. Betancor
Affiliation:
Departamento de Análisis Matemático, Universidad de la Laguna, Campus de Anchieta, Avda. Astrofísico Francisco Sánchez, s/n 38271 La Laguna (Sta Cruz de Tenerife), Spain (jbetanco@ull.es)
R. Crescimbeni
Affiliation:
Departamento de Matemática, Universidad Nacional de Comahue, Buenos Aires 1400, 8300 Neuquén, Argentina (rcrescim@uncoma.edu.ar)
J. L. Torrea
Affiliation:
Departamento de Matemáticas and ICMAT-CSIC-UAM-UCM-UC3M, Facultad de Ciencias, Universidad Autónoma de Madrid, 28049 Madrid, Spain (joseluis.torrea@uam.es)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 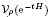, ρ > 2, be the ρ-variation of the heat semigroup associated to the harmonic oscillator H = ½(−Δ + |x|2). We show that if f ∈ L∞ (ℝ), the 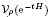(f)(x) < ∞, a.e. x ∈ ℝ. However, we find a function G ∈ L∞ (ℝ), such that 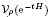(G)(x) ∉ L∞ (ℝ). We also analyse the local behaviour in L∞ of the operator 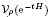. We find that its growth is smaller than that of a standard singular integral operator. As a by-product of our work we obtain an L∞ (ℝ) function F, such that the square function

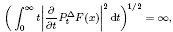
a.e. x ∈ ℝ, where 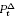is the classical Poisson kernal in ℝ.

Keywords

Hermite operatorρ-variationheat semigroupPoisson semigroup

MSC classification

Secondary: 42C05: Orthogonal functions and polynomials, general theory 42C15: General harmonic expansions, frames
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 54 , Issue 3 , October 2011 , pp. 569 - 585
Copyright
Copyright © Edinburgh Mathematical Society 2011

References

1.Campbell, J. T., Jones, R. L., Reinhold, K. and Wierdl, M., Oscillation and variation for the Hilbert transform, Duke Math. J. 105(1) (2000), 59–83.CrossRefGoogle Scholar
2.Crescimbeni, R., Maciáas, R. A., Menárguez, T., Torrea, J. L. and Viviani, B., The ρ-variation as an operator between maximal operators and singular integrals, J. Evol. Eqns 9(1) (2009), 81–102.CrossRefGoogle Scholar
3.Jones, R. L., Kaufman, R., Rosenblatt, J. M. and Wierdl, M., Oscillation in ergodic theory, Ergod. Theory Dynam. Syst. 18 (1998), 889–935.CrossRefGoogle Scholar
4.Jones, R. L. and Reinhold, K., Oscillation and variation inequalities for convolution powers, Ergod. Theory Dynam. Syst. 21(6) (2001), 1809–1829.CrossRefGoogle Scholar
5.Jones, R. L., Seeger, A. and Wright, J., Strong variational and jump inequalities in harmonic analysis, Trans. Am. Math. Soc. 360(12) (2008), 6711–6742.CrossRefGoogle Scholar
6.Oberlin, R., Seeger, A., Tao, T., Thiele, C. and Wright, J., A variation norm Carleson theorem, preprint (arXiv:0910.1555v2; 2010).Google Scholar
7.Stempak, K. and Torrea, J. L., Poisson integrals and Riesz transforms for Hermite function expansions with weights, J. Funct. Analysis 202(2) (2003), 443–472.CrossRefGoogle Scholar
8.Thangavelu, S., Lectures on Hermite and Laguerre expansions, Mathematical Notes, Volume 42 (Princeton University Press, 1993).CrossRefGoogle Scholar
9.Wang, S., Some properties of Littlewood–Paley's g-function, Sci. Sinica A28(3) (1985), 252–262.Google Scholar
10.Wang, S., Some properties of the Littlewood–Paley g-function, in Classical real analysis, Contemporary Mathematics, Volume 42, pp. 191–202 (American Mathematical Society, Providence, RI, 1985).CrossRefGoogle Scholar