Research Article
The tensor product of distributive lattices: structural results
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 237-245
-
- Article
-
- You have access
- Export citation
On radicals of finite near-rings
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 247-259
-
- Article
-
- You have access
- Export citation
On the generalized heat-equation
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 261-273
-
- Article
-
- You have access
- Export citation
Non-orthogonalisable vector fields on spheres
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 275-281
-
- Article
-
- You have access
- Export citation
Indicial equivalents of multiparameter definiteness conditions in finite dimensions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 283-296
-
- Article
-
- You have access
- Export citation
The strong maximum principle for the heat equation*
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 297-299
-
- Article
-
- You have access
- Export citation
Counterexamples in intersections for C*-tensor products
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 301-302
-
- Article
-
- You have access
- Export citation
On the unique solvability of a class of modified boundary integral equations
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 303-311
-
- Article
-
- You have access
- Export citation
Free non-associative principal train algebras
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 313-319
-
- Article
-
- You have access
- Export citation
Stability of barrelledness and related concepts in topological vector spaces
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 321-325
-
- Article
-
- You have access
- Export citation
Sur l'image d'une fonction entiere de deux variables complexes
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 327-331
-
- Article
-
- You have access
- Export citation
On the mutagenic radical property
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 333-336
-
- Article
-
- You have access
- Export citation
Associativity of the tensor product of semilattices
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 337-340
-
- Article
-
- You have access
- Export citation
Young tableaux and longest monotone subsequences: An inequality and a conjecture
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 341-344
-
- Article
-
- You have access
- Export citation
Book Reviews
J. Aczél (ed.), Functional equations: history, applications and theory (D. Reidel, Dordrecht1984), pp. ix + 244, Dfl. 125.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 345-346
-
- Article
-
- You have access
- Export citation
B. A. Barnes, G. J. Murphy, M. R. F. Smyth and T. T. West, Riesz and Fredholm theory in Banach algebras (Research Notes in Mathematics 67, Pitman, 1982), 123 pp, £7.95.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 346
-
- Article
-
- You have access
- Export citation
K. T. Smith, Primer of modern analysis (Springer-Verlag, 2nd ed.1983), xv + 446 pp. DM97.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 346-347
-
- Article
-
- You have access
- Export citation
Wilhelm Blaschke, Gesammelte Werke, Band I ed. by W. Burau, S. S. Chern et al. (Thales-Verlag, Essen1982), pp. 365.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 347-349
-
- Article
-
- You have access
- Export citation
J. Diestel, Sequences and series in Banach spaces (Graduate Texts in Mathematics Vol. 92, Springer-Verlag, Berlin-Heidelberg-New York, 1984) xiii + 261 pp., DM 108.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 349
-
- Article
-
- You have access
- Export citation
P. A. Perry, Scattering theory by the Enss method (Mathematical Reports Vol. 1, Part 1, Harwood Academic Publishers, New York, 1983) xiv + 347 pp., $82.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 350
-
- Article
-
- You have access
- Export citation

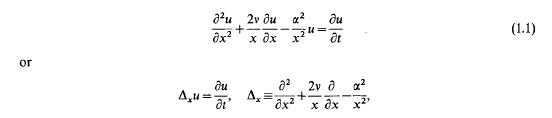
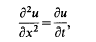
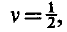 , then (1.1) becomes
, then (1.1) becomes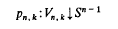
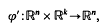
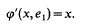
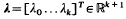 satisfying
satisfying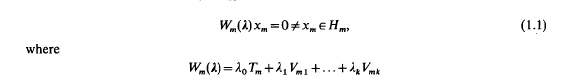
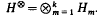 We shall connect his work with more recent investigations [5,7] of eigenvalue indices based on minimax principles for
We shall connect his work with more recent investigations [5,7] of eigenvalue indices based on minimax principles for 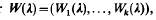 , which can be viewed as an operator on
, which can be viewed as an operator on 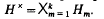 .
.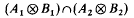 strictly contains
strictly contains 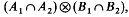 , answering a question of S. Wassermann [3, Remark 23]. In this short note, we show that the same situation can occur even if
, answering a question of S. Wassermann [3, Remark 23]. In this short note, we show that the same situation can occur even if 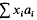 in basis elements
in basis elements 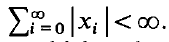 In this paper I consider only algebras whose elements are forms
In this paper I consider only algebras whose elements are forms 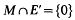 and dim
and dim 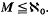 Robertson, Tweddle and Yeomans have recently considered the question of barrelledness under the Mackey topology τ(
Robertson, Tweddle and Yeomans have recently considered the question of barrelledness under the Mackey topology τ(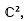 , Θ ayant un point fixe attractif z
, Θ ayant un point fixe attractif z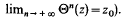 Alors d'aprés un résultat bien connu, il existe une fonction
Alors d'aprés un résultat bien connu, il existe une fonction 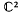 dans
dans 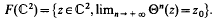 Ceci provient du fait qu'il existe une fonction
Ceci provient du fait qu'il existe une fonction 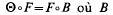 est un automorphisme analytique de
est un automorphisme analytique de 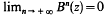 pour tout z élément de
pour tout z élément de 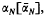 , the length (i.e. number of terms) of a longest monotone increasing [decreasing] subsequence of (not necessarily consecutive) terms in a random permutation of the first
, the length (i.e. number of terms) of a longest monotone increasing [decreasing] subsequence of (not necessarily consecutive) terms in a random permutation of the first 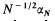 converges almost surely to 2 [
converges almost surely to 2 [