Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-25T01:35:15.769Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-orthogonalisable vector fields on spheres

Published online by Cambridge University Press:  20 January 2009

Martin Raussen
Martin Raussen
Affiliation:
Mathematissches Institut der Universität GöttingenBunsenstrasse 3/5, D 3400 Göttingen Matematisk Institut, Aarhus UniversitetNy Munkegade, DK-8000 Aarhus C
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A (k – l)-field on Sn-1 may be given as a section ϕ of the fibre bundle

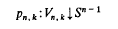
with fibre Vn-1, k-1 or, equivalently, as a semi-orthogonal map, i.e., a map

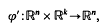
which is isometric in the second variable and such that for the basis vector e1∈Rk and every x∈Rn

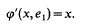
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 27 , Issue 3 , October 1984 , pp. 275 - 281
Copyright
Copyright © Edinburgh Mathematical Society 1984

References

REFERENCES

1.Adams, J. F.On the groups J(X) IV, Topology 5 (1966), 21–71.CrossRefGoogle Scholar
2.Atiyah, M. F., Bott, R. and Shapiro, A.Clifford modules, Topology 3 (Supplement 1) (1964), 3–38.CrossRefGoogle Scholar
3.Bier, TH. and Schwardmann, U.Räume normierter Bilinearformen und Cliffordstrukturen, Math. Z. 180 (1982), 203–215.CrossRefGoogle Scholar
4.Eckmann, B.Gruppentheoretischer Beweis des Satzes von Hurwitz-Radon über die Komposition quadratischer Formen, Comment. Math. Helv. 15 (1943), 358–366.CrossRefGoogle Scholar
5.Hefter, H.Dehnungsuntersuchungen an Spharenabbildungen, Invent. Math. 66 (1982), 1–10.CrossRefGoogle Scholar
6.James, I. M.The topology of Stiefel manifolds (Cambridge University Press, 1976).Google Scholar
7.James, I. M. and Thomas, E.Note on the classification of cross-sections, Topology 4 (1966), 351–359.CrossRefGoogle Scholar
8.Lam, K. Y.On the bilinear and skew-linear maps that are non-singular, Quart. J. Oxford 19 (1968), 281–288.CrossRefGoogle Scholar
9.Milgram, R. J. and Zvengrowski, P., Skewness of r-fields on spheres, Topology 15 (1976), 325-336.CrossRefGoogle Scholar
10.Paechter, G. F.The groups V n ,m-I, Quart. J. of-Math. Oxford 7 (1956), 249–269.CrossRefGoogle Scholar
11.Raussen, M. and Smith, L.A geometric interpretation of sphere bundle boundaries and generalized J-homomorphisms with an application to a diagram of I. M. James, Quart. J. Oxford 30 (1979), 113–117.Google Scholar
12.Smith, L.Nonsingular bilinear forms, generalized J-homomorphisms and the homotopy of spheres I, Ind. V. Math. J.. 27 (1978), 697–737.CrossRefGoogle Scholar
13.Toda, H.p-primary components of homotopy groups III. Stable groups of the sphere, Mem. Coll. Sri. Univ. Kyoto Ser. A Math. 31 (1958), 191–210.Google Scholar
14.Toda, H.Composition method in homotopy groups of spheres (Ann. of Math.) Studies 49, Princeton University Press, 1962.Google Scholar