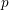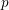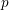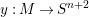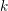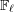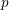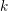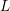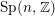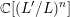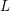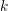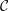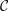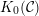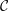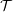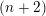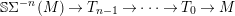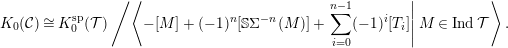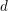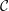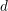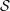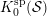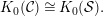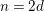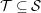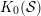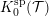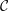Article
LOCAL DUALITY FOR THE SINGULARITY CATEGORY OF A FINITE DIMENSIONAL GORENSTEIN ALGEBRA
- Part of:
-
- Published online by Cambridge University Press:
- 11 March 2020, pp. 1-24
-
- Article
- Export citation
BERNSTEIN–SATO ROOTS FOR MONOMIAL IDEALS IN POSITIVE CHARACTERISTIC
- Part of:
-
- Published online by Cambridge University Press:
- 20 March 2020, pp. 25-34
-
- Article
- Export citation
WEIERSTRASS–KENMOTSU REPRESENTATION OF WILLMORE SURFACES IN SPHERES
- Part of:
-
- Published online by Cambridge University Press:
- 27 April 2020, pp. 35-59
-
- Article
- Export citation
GENERATORS, RELATIONS, AND HOMOLOGY FOR OZSVÁTH–SZABÓ’S KAUFFMAN-STATES ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 17 April 2020, pp. 60-118
-
- Article
- Export citation
CHARACTERIZING THE MOD-
 $\ell$ LOCAL LANGLANDS CORRESPONDENCE BY NILPOTENT GAMMA FACTORS
$\ell$ LOCAL LANGLANDS CORRESPONDENCE BY NILPOTENT GAMMA FACTORS
- Part of:
-
- Published online by Cambridge University Press:
- 12 May 2020, pp. 119-135
-
- Article
- Export citation
MASS GROWTH OF OBJECTS AND CATEGORICAL ENTROPY
- Part of:
-
- Published online by Cambridge University Press:
- 04 June 2020, pp. 136-157
-
- Article
- Export citation
DEGENERATING 0 IN TRIANGULATED CATEGORIES
- Part of:
-
- Published online by Cambridge University Press:
- 08 June 2020, pp. 158-167
-
- Article
- Export citation
ANALYTIC PROPERTIES OF EISENSTEIN SERIES AND STANDARD
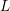 $L$-FUNCTIONS
$L$-FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 21 July 2020, pp. 168-203
-
- Article
- Export citation
GROTHENDIECK GROUPS OF TRIANGULATED CATEGORIES VIA CLUSTER TILTING SUBCATEGORIES
- Part of:
-
- Published online by Cambridge University Press:
- 11 June 2020, pp. 204-231
-
- Article
- Export citation
HIGHER DEFORMATIONS OF LIE ALGEBRA REPRESENTATIONS II
- Part of:
-
- Published online by Cambridge University Press:
- 02 June 2020, pp. 232-255
-
- Article
- Export citation
MINIMAL MODEL THEORY FOR LOG SURFACES IN FUJIKI’S CLASS
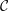 ${\mathcal{C}}$
${\mathcal{C}}$
- Part of:
-
- Published online by Cambridge University Press:
- 05 June 2020, pp. 256-282
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TOPOLOGIES ON SCHEMES AND MODULUS PAIRS
- Part of:
-
- Published online by Cambridge University Press:
- 13 July 2020, pp. 283-313
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
NMJ volume 244 Cover and Front matter
-
- Published online by Cambridge University Press:
- 08 November 2021, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
NMJ volume 244 Cover and Back matter
-
- Published online by Cambridge University Press:
- 08 November 2021, pp. b1-b2
-
- Article
-
- You have access
- Export citation