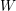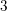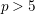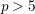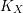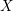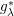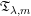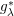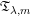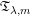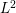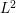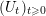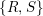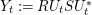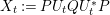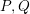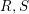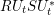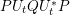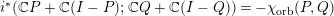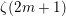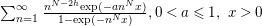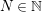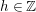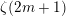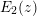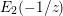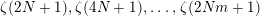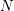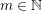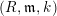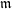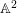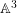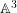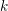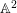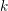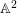Article
ON CANONICAL BASES AND INDUCTION OF
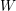 $W$-GRAPHS
$W$-GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 17 July 2018, pp. 1-41
-
- Article
- Export citation
NOTES ON TORIC VARIETIES FROM MORI THEORETIC VIEWPOINT, II
- Part of:
-
- Published online by Cambridge University Press:
- 29 August 2018, pp. 42-75
-
- Article
- Export citation
FINITENESS OF LOG MINIMAL MODELS AND NEF CURVES ON
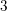 $3$-FOLDS IN CHARACTERISTIC
$3$-FOLDS IN CHARACTERISTIC 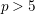 $p>5$
$p>5$
- Part of:
-
- Published online by Cambridge University Press:
- 10 September 2018, pp. 76-109
-
- Article
- Export citation
NO COHOMOLOGICALLY TRIVIAL NONTRIVIAL AUTOMORPHISM OF GENERALIZED KUMMER MANIFOLDS
- Part of:
-
- Published online by Cambridge University Press:
- 05 November 2018, pp. 110-122
-
- Article
- Export citation
ON THE BILINEAR SQUARE FOURIER MULTIPLIER OPERATORS ASSOCIATED WITH
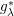 $g_{\unicode[STIX]{x1D706}}^{\ast }$ FUNCTION
$g_{\unicode[STIX]{x1D706}}^{\ast }$ FUNCTION
- Part of:
-
- Published online by Cambridge University Press:
- 28 August 2018, pp. 123-152
-
- Article
- Export citation
THE OPTIMAL JET
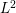 $L^{2}$ EXTENSION OF OHSAWA–TAKEGOSHI TYPE
$L^{2}$ EXTENSION OF OHSAWA–TAKEGOSHI TYPE
- Part of:
-
- Published online by Cambridge University Press:
- 20 September 2018, pp. 153-172
-
- Article
- Export citation
FOUR IDENTITIES FOR THIRD ORDER MOCK THETA FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 21 September 2018, pp. 173-204
-
- Article
- Export citation
LIBERATION, FREE MUTUAL INFORMATION AND ORBITAL FREE ENTROPY
- Part of:
-
- Published online by Cambridge University Press:
- 14 September 2018, pp. 205-231
-
- Article
- Export citation
GENERALIZED LAMBERT SERIES, RAABE’S COSINE TRANSFORM AND A GENERALIZATION OF RAMANUJAN’S FORMULA FOR
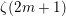 $\unicode[STIX]{x1D701}(2m+1)$
$\unicode[STIX]{x1D701}(2m+1)$
- Part of:
-
- Published online by Cambridge University Press:
- 04 October 2018, pp. 232-293
-
- Article
- Export citation
ON THE GALOIS STRUCTURE OF ARITHMETIC COHOMOLOGY I: COMPACTLY SUPPORTED
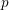 $p$-ADIC COHOMOLOGY
$p$-ADIC COHOMOLOGY
- Part of:
-
- Published online by Cambridge University Press:
- 16 November 2018, pp. 294-321
-
- Article
- Export citation
CONTINUITY OF HILBERT–KUNZ MULTIPLICITY AND F-SIGNATURE
- Part of:
-
- Published online by Cambridge University Press:
- 27 December 2018, pp. 322-345
-
- Article
- Export citation
ON SEPARABLE
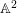 $\mathbb{A}^{2}$ AND
$\mathbb{A}^{2}$ AND 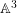 $\mathbb{A}^{3}$-FORMS
$\mathbb{A}^{3}$-FORMS
- Part of:
-
- Published online by Cambridge University Press:
- 26 December 2018, pp. 346-354
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
NMJ volume 239 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 August 2020, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
NMJ volume 239 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 August 2020, pp. b1-b2
-
- Article
-
- You have access
- Export citation