Research Article
A note on trigonometric sums in several variables
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 189-193
-
- Article
- Export citation
Perfect powers in values of certain polynomials at integer points
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 195-207
-
- Article
- Export citation
Extensions of pro-p groups of cohomological dimension two
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 209-211
-
- Article
- Export citation
Real forms of cusp singularities
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 213-232
-
- Article
- Export citation
Inequivalent, bordant group actions on a surface
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 233-238
-
- Article
- Export citation
An infinite family of non-Haken hyperbolic 3-manifolds with vanishing Whitehead groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 239-246
-
- Article
- Export citation
Threading knot diagrams
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 247-260
-
- Article
- Export citation
Another ‘short’ proof of the Riesz representation theorem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 261-262
-
- Article
- Export citation
Estimates for polynomial norms on Lp(μ) spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 263-271
-
- Article
- Export citation
Continuity of Arens multiplication on the dual space of bounded uniformly continuous functions on locally compact groups and topological semigroups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 273-283
-
- Article
- Export citation
The packing measure of rectifiable subsets of the plane
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 285-296
-
- Article
- Export citation
Bernstein's theorem for compact, connected Lie groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 297-305
-
- Article
- Export citation
Smooth derivations commuting with Lie group actions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 307-314
-
- Article
- Export citation
Connectivity of finite anisotropic random graphs and directed graphs
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 315-330
-
- Article
- Export citation
Continuum structures. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 331-338
-
- Article
- Export citation
A fixed point approach to local minimax theory
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 339-346
-
- Article
- Export citation
On convergence and quasiconformality of complex planar spline interpolants
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 347-356
-
- Article
- Export citation
Uniqueness and continuous dependence in the linear elastodynamic exterior and half-space problems
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 357-366
-
- Article
- Export citation
Curvature, causality and completeness in space-times with causally complete spacelike slices
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 367-375
-
- Article
- Export citation
Corrigenda
Corrigenda
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 377-379
-
- Article
-
- You have access
- Export citation

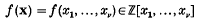
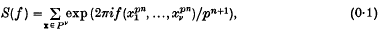

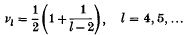
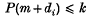
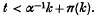
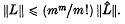
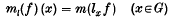
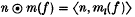
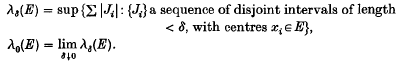
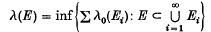


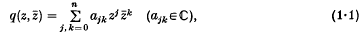
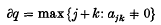
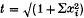 in Minkowski space (where (
in Minkowski space (where (