Research Article
Cohomological annihilators
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 345-350
-
- Article
- Export citation
On the tangent developable of a space curve
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 351-355
-
- Article
- Export citation
On the law of nullity
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 357-374
-
- Article
- Export citation
Boolean powers of groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 375-396
-
- Article
- Export citation
Groups whose irreducible representations have finite degree: III
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 397-406
-
- Article
- Export citation
The asymmetry of M0(G)
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 407-433
-
- Article
- Export citation
Series identities and reducibility of Kampé de Fériet functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 435-440
-
- Article
- Export citation
Some conditions ensuring the vanishing of harmonic differential forms with applications to harmonic maps and Yang-Mills theory
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 441-452
-
- Article
- Export citation
On the converse of absolute Abel summability
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 453-456
-
- Article
- Export citation
A theorem about countable decomposability
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 457-458
-
- Article
- Export citation
Locally symmetric homology spheres and an application of Matsushima's formula
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 459-466
-
- Article
- Export citation
Totally knotted knots are prime
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 467-472
-
- Article
- Export citation
More 3-manifolds with multiple knot-surgery and branched-cover descriptions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 473-475
-
- Article
- Export citation
Probability measures with trivial Stam groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 477-484
-
- Article
- Export citation
On polynomial symmetries of the sine-Gordon equation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 485-489
-
- Article
- Export citation
Surface instabilities on an equibiaxially stretched elastic half-space
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 491-501
-
- Article
- Export citation
Some orthogonal and complete sets of Bessel functions associated with the vibrating plate
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 503-515
-
- Article
- Export citation
Front matter
PSP volume 91 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 91 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b24
-
- Article
-
- You have access
- Export citation

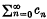 is said to be summable
is said to be summable 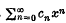 converges to φ(
converges to φ(