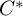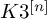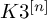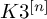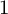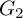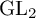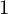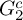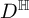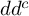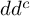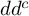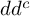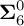Open access
Research Article
COHOMOLOGIE DE DE RHAM DU REVÊTEMENT MODÉRÉ DE L’ESPACE DE DRINFELD
-
- Published online by Cambridge University Press:
- 28 May 2024, pp. 1-43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWISTED GAN–GROSS–PRASAD CONJECTURE FOR CERTAIN TEMPERED L-PACKETS
- Part of:
-
- Published online by Cambridge University Press:
- 24 May 2024, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ARCHIMEDEAN NEWFORM THEORY FOR
 $\operatorname {\mathrm {GL}}_n$
$\operatorname {\mathrm {GL}}_n$
- Part of:
-
- Published online by Cambridge University Press:
- 17 May 2024, pp. 1-76
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Addendum
ADDENDUM: REAL TOPOLOGICAL HOCHSCHILD HOMOLOGY OF SCHEMES
-
- Published online by Cambridge University Press:
- 08 May 2024, pp. 1519-1520
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Research Article
WILES DEFECT OF HECKE ALGEBRAS VIA LOCAL-GLOBAL ARGUMENTS: WITH AN APPENDIX BY NAJMUDDIN FAKHRUDDIN AND CHANDRASHEKHAR B. KHARE
- Part of:
-
- Published online by Cambridge University Press:
- 25 April 2024, pp. 1-81
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
KOBAYASHI-OCHIAI’S FINITENESS THEOREM FOR ORBIFOLD PAIRS OF GENERAL TYPE
- Part of:
-
- Published online by Cambridge University Press:
- 17 April 2024, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENERALISED QUADRATIC FORMS OVER TOTALLY REAL NUMBER FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 11 April 2024, pp. 1-54
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Correction
THE p-ADIC GROSS–ZAGIER FORMULA ON SHIMURA CURVES, II: NONSPLIT PRIMES – CORRIGENDUM
-
- Published online by Cambridge University Press:
- 02 April 2024, pp. 1-6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Research Article
DYNAMICAL MCDUFF-TYPE PROPERTIES FOR GROUP ACTIONS ON VON NEUMANN ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 02 April 2024, pp. 1-37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THERMODYNAMIC FORMALISM FOR AMENABLE GROUPS AND COUNTABLE STATE SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 15 March 2024, pp. 1-65
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ENERGY BOUNDS FOR MODULAR ROOTS AND THEIR APPLICATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1-42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PERFECTING GROUP SCHEMES
- Part of:
-
- Published online by Cambridge University Press:
- 16 February 2024, pp. 1-43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LIMIT SETS OF UNFOLDING PATHS IN OUTER SPACE
- Part of:
-
- Published online by Cambridge University Press:
- 15 February 2024, pp. 1-39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A CATEGORICAL APPROACH TO THE BAUM–CONNES CONJECTURE FOR ÉTALE GROUPOIDS
- Part of:
-
- Published online by Cambridge University Press:
- 02 January 2024, pp. 1-46
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RIGID STABLE VECTOR BUNDLES ON HYPERKÄHLER VARIETIES OF TYPE
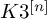 $K3^{[n]}$
$K3^{[n]}$
-
- Published online by Cambridge University Press:
- 22 December 2023, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COUNTING DISCRETE, LEVEL-
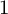 $1$, QUATERNIONIC AUTOMORPHIC REPRESENTATIONS ON
$1$, QUATERNIONIC AUTOMORPHIC REPRESENTATIONS ON 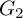 $G_2$
$G_2$
- Part of:
-
- Published online by Cambridge University Press:
- 13 December 2023, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GALOIS REPRESENTATIONS FOR EVEN GENERAL SPECIAL ORTHOGONAL GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 13 December 2023, pp. 1-92
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON LARGE EXTERNALLY DEFINABLE SETS IN NIP
- Part of:
-
- Published online by Cambridge University Press:
- 04 December 2023, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A
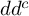 $dd^c$-TYPE CONDITION BEYOND THE KÄHLER REALM
$dd^c$-TYPE CONDITION BEYOND THE KÄHLER REALM
- Part of:
-
- Published online by Cambridge University Press:
- 28 November 2023, pp. 1-54
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POLISH SPACES OF BANACH SPACES: COMPLEXITY OF ISOMETRY AND ISOMORPHISM CLASSES
- Part of:
-
- Published online by Cambridge University Press:
- 28 November 2023, pp. 1-39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation