Research Article
The AND/OR Theorem for Perceptrons
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-8
-
- Article
-
- You have access
- Export citation
M-Cohyponormal powers of composition operators
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 9-16
-
- Article
-
- You have access
- Export citation
Self-complementary graph decompositions
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 17-24
-
- Article
-
- You have access
- Export citation
Fixed points of mappings satisfying semicontractivity conditions
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 25-38
-
- Article
-
- You have access
- Export citation
Uniform distribution and lattice point counting
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 39-50
-
- Article
-
- You have access
- Export citation
An open mapping theorem on homogeneous spaces
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 51-54
-
- Article
-
- You have access
- Export citation
On prime one-sided ideals, bi-ideals and quasi-ideals of a gamma ring
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 55-63
-
- Article
-
- You have access
- Export citation
Preorders on canonical families of modules of finite length
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 64-77
-
- Article
-
- You have access
- Export citation
Metrical properties of best approximants
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 78-91
-
- Article
-
- You have access
- Export citation
Multiplication Operators and Dynamical Systems
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 92-102
-
- Article
-
- You have access
- Export citation
Ideals and other generalizations of congruence classes
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 103-115
-
- Article
-
- You have access
- Export citation
Periodic groups with many permutable subgroups
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 116-119
-
- Article
-
- You have access
- Export citation
Nilpotent-by-Černikov CC-groups
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 120-130
-
- Article
-
- You have access
- Export citation
Certain inequalities involving fractional powers
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 131-136
-
- Article
-
- You have access
- Export citation
On unilateral shift operators and C0-operators
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 137-142
-
- Article
-
- You have access
- Export citation
Front matter
JAZ volume 53 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Back matter
JAZ volume 53 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

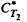 with respect to
with respect to 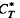 and
and 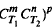 ]* is
]* is 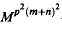 -hyponormal. As a consequence, we see that if
-hyponormal. As a consequence, we see that if 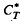 is an M-hyponormal composition operator, then
is an M-hyponormal composition operator, then 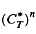 is
is 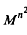 -hyponormal for all positive integers
-hyponormal for all positive integers 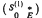 relative to a decomposition ℳ ⊕
relative to a decomposition ℳ ⊕