The threshold for the resonant destabilisation of ion-temperature-gradient (ITG) driven instabilities that render the modes ubiquitous in both tokamaks and stellarators is investigated. We discover remarkably similar results for both confinement concepts if care is taken in the analysis of the effect of the global shear 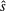${\hat{s}}$. We revisit, analytically and by means of gyrokinetic simulations, accepted tokamak results and discover inadequacies of some aspects of their theoretical interpretation. In particular, for standard tokamak configurations, we find that global shear effects on the critical gradient cannot be attributed to the wave–particle resonance destabilising mechanism of Hahm & Tang (Phys. Plasmas, vol. 1, 1989, pp. 1185–1192), but are consistent with a stabilising contribution predicted by Biglari et al. (Phys. Plasmas, vol. 1, 1989, pp. 109–118). Extensive analytical and numerical investigations show that virtually no previous tokamak theoretical predictions capture the temperature dependence of the mode frequency at marginality, thus leading to incorrect instability thresholds. In the asymptotic limit 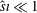${\hat{s}}\unicode[STIX]{x1D704}\ll 1$, where $\unicode[STIX]{x1D704}$ is the rotational transform, and such a threshold should be solely determined by the resonant toroidal branch of the ITG mode, we discover a family of unstable solutions below the previously known threshold of instability. 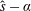This is true for a tokamak case described by a local ${\hat{s}}-\unicode[STIX]{x1D6FC}$ local equilibrium, and for the stellarator Wendelstein 7-X, where these unstable solutions are present even for configurations with a small trapped-particle population. We conjecture they are of the Floquet type and derive their properties from the Fourier analysis of toroidal drift modes of Connor & Taylor (Phys. Fluids, vol. 30, 1987, pp. 3180–3185), and to Hill’s theory of the motion of the lunar perigee (Acta Math., vol. 8, 1886, pp. 1–36). The temperature dependence of the newly determined threshold is given for both confinement concepts. In the first case, the new temperature-gradient threshold is found to be rather insensitive to the temperature ratio 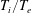$T_{i}/T_{e}$, at least for 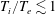$T_{i}/T_{e}\lesssim 1$, and to be a growing function of the density gradient scale for 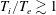$T_{i}/T_{e}\gtrsim 1$. For Wendelstein 7-X, the new critical temperature gradient is a growing function of the temperature ratio. The importance of these findings for the assessment of turbulence in stellarators and low-shear tokamak configurations is discussed.

We have performed two-dimensional hybrid simulations of non-relativistic collisionless shocks in the presence of pre-existing energetic particles (‘seeds’); such a study applies, for instance, to the re-acceleration of galactic cosmic rays (CRs) in supernova remnant (SNR) shocks and solar wind energetic particles in heliospheric shocks. Energetic particles can be effectively reflected and accelerated regardless of shock inclination via a process that we call diffusive shock re-acceleration. We find that re-accelerated seeds can drive the streaming instability in the shock upstream and produce effective magnetic field amplification. This can eventually trigger the injection of thermal protons even at oblique shocks that ordinarily cannot inject thermal particles. We characterize the current in reflected seeds, finding that it tends to a universal value $J\simeq en_{\text{CR}}v_{\text{sh}}$, where $en_{\text{CR}}$ is the seed charge density and $v_{\text{sh}}$ is the shock velocity. When applying our results to SNRs, we find that the re-acceleration of galactic CRs can excite the Bell instability to nonlinear levels in less than ${\sim}10~\text{yr}$, thereby providing a minimum level of magnetic field amplification for any SNR shock. Finally, we discuss the relevance of diffusive shock re-acceleration also for other environments, such as heliospheric shocks, galactic superbubbles and clusters of galaxies.

An electromagnetic reduced gyrofluid model for collisionless plasmas, accounting for electron inertia, finite ion Larmor radius effects and Landau-fluid closures for the electron fluid is derived by means of an asymptotic expansion from a parent gyrofluid model. In the absence of terms accounting for Landau damping, the model is shown to possess a non-canonical Hamiltonian structure. The corresponding Casimir invariants are derived and use is made thereof, in order to obtain a set of normal field variables, in terms of which the Poisson bracket and the model equations take a remarkably simple form. The inclusion of perpendicular temperature fluctuations generalizes previous Hamiltonian reduced fluid models and, in particular, the presence of ion perpendicular gyrofluid temperature fluctuations reflects into the presence of two new Lagrangian invariants governing the ion dynamics. The model is applied, in the cold-ion limit, to investigate numerically a magnetic reconnection problem. The Landau damping terms are shown to reduce, by decreasing the electron temperature fluctuations, the linear reconnection rate and to delay the nonlinear island growth. The saturated island width, on the other hand, is independent of Landau damping. The fraction of magnetic energy converted into perpendicular kinetic energy also appears to be unaffected by the Landau damping terms, which, on the other hand, dissipate parallel kinetic energy as well as free energy due to density and electron temperature fluctuations.

In this paper, the stability of Newtonian and non-Newtonian viscoelastic collisional shear-velocity dusty plasmas is studied, using the framework of a generalized hydrodynamic (GH) model. Motivated by Banerjee et al.’s work (Banerjee et al., New J. Phys., vol. 12 (12), 2010, p. 123031), employing linear perturbation theory as well as the local approximation method in the inhomogeneous direction, the dispersion relations of the Fourier modes are obtained for Newtonian and non-Newtonian dusty plasma systems in the presence of a dust–neutral friction term. The analysis of the obtained dispersion relation in the non-Newtonian case shows that the inhomogeneous viscosity force depending on the velocity shear profile can be the genesis of a free energy source which leads the shear system to be unstable. Study of the dust–neutral friction effect on the instability of the considered systems using numerical analysis of the dispersion relation in the Newtonian case demonstrates that the maximum growth rate decreases considerably by increasing the collision frequency in the hydrodynamic regime, while this reduction can be neglected in the kinetic regime. Results show a more significant stabilization role of the dust–neutral friction term in the non-Newtonian cases, through decreasing the maximum growth rate at any fixed wavenumber and construction of the instable wavenumber region. The results of the present investigation will greatly contribute to study of the time evolution of viscoelastic laboratory environments with externally applied shear; where in these experiments the dust–neutral friction process can play a considerable role.

Particle transport, acceleration and energization are phenomena of major importance for both space and laboratory plasmas. Despite years of study, an accurate theoretical description of these effects is still lacking. Validating models with self-consistent, kinetic simulations represents today a new challenge for the description of weakly collisional, turbulent plasmas. We perform simulations of steady state turbulence in the 2.5-dimensional approximation (three-dimensional fields that depend only on two-dimensional spatial directions). The chosen plasma parameters allow to span different systems, going from the solar corona to the solar wind, from the Earth’s magnetosheath to confinement devices. To describe the ion diffusion we adapted the nonlinear guiding centre (NLGC) theory to the two-dimensional case. Finally, we investigated the local influence of coherent structures on particle energization and acceleration: current sheets play an important role if the ions’ Larmor radii are of the order of the current sheet’s size. This resonance-like process leads to the violation of the magnetic moment conservation, eventually enhancing the velocity-space diffusion.

We consider the one-dimensional equilibrium problem of a shear-flow boundary layer within an ‘extended-fluid model’ of a plasma that includes the Hall and the electron pressure terms in Ohm’s law, as well as dynamic equations for anisotropic pressure for each species and first-order finite-Larmor-radius (FLR) corrections to the ion dynamics. We provide a generalized version of the analytic expressions for the equilibrium configuration given in Cerri et al., (Phys. Plasmas, vol. 20 (11), 2013, 112112), highlighting their intrinsic asymmetry due to the relative orientation of the magnetic field $\boldsymbol{B}$, $\boldsymbol{b}=\boldsymbol{B}/|\boldsymbol{B}|$, and the fluid vorticity $\unicode[STIX]{x1D74E}=\unicode[STIX]{x1D735}\times \boldsymbol{u}$ (‘$\unicode[STIX]{x1D74E}\boldsymbol{b}$ asymmetry’). Finally, we show that FLR effects can modify the Chapman–Ferraro current layer at the flank magnetopause in a way that is consistent with the observed structure reported by Haaland et al., (J. Geophys. Res. (Space Phys.), vol. 119, 2014, pp. 9019–9037). In particular, we are able to qualitatively reproduce the following key features: (i) the dusk–dawn asymmetry of the current layer, (ii) a double-peak feature in the current profiles and (iii) adjacent current sheets having thicknesses of several ion Larmor radii and with different current directions.

We develop a model of gamma-ray flares of the Crab Nebula resulting from the magnetic reconnection events in a highly magnetised relativistic plasma. We first discuss physical parameters of the Crab Nebula and review the theory of pulsar winds and termination shocks. We also review the principle points of particle acceleration in explosive reconnection events [Lyutikov et al., J. Plasma Phys., vol. 83(6), p. 635830601 (2017a); J. Plasma Phys., vol. 83(6), p. 635830602 (2017b)]. It is required that particles producing flares are accelerated in highly magnetised regions of the nebula. Flares originate from the poleward regions at the base of the Crab’s polar outflow, where both the magnetisation and the magnetic field strength are sufficiently high. The post-termination shock flow develops macroscopic (not related to the plasma properties on the skin-depth scale) kink-type instabilities. The resulting large-scale magnetic stresses drive explosive reconnection events on the light-crossing time of the reconnection region. Flares are produced at the initial stage of the current sheet development, during the X-point collapse. The model has all the ingredients needed for Crab flares: natural formation of highly magnetised regions, explosive dynamics on the light travel time, development of high electric fields on macroscopic scales and acceleration of particles to energies well exceeding the average magnetic energy per particle.

An analytic theory is presented of magnetic structures in collisionless, high-$\unicode[STIX]{x1D6FD}$ plasmas. Using a reduced magnetohydrodynamic model, a stationary nonlinear solution is constructed in the form of a Kelvin–Stuart cat’s eyes chain of magnetic islands, on the spatial scale that exceeds the characteristic ion lengths. The solution is imbedded in a background current sheet and possesses both a significant plasma density perturbation trapped inside the magnetic islands and a compressional magnetic field component that is driven mostly by a current loop located at the separatrix of the islands. This theory may provide an explanation for the magnetic structures observed in the solar wind close to the Earth by the Cluster spacecraft.

The nonlinear dynamics of energetic-particle (EP) driven geodesic acoustic modes (EGAM) in tokamaks is investigated, and compared with the beam-plasma system (BPS). The EGAM is studied with the global gyrokinetic (GK) particle-in-cell code ORB5, treating the thermal ions and EP (in this case, fast ions) as GK and neglecting the kinetic effects of the electrons. The wave–particle nonlinearity is only considered in the EGAM nonlinear dynamics. The BPS is studied with a one-dimensional code where the thermal plasma is treated as a linear dielectric, and the EP (in this case, fast electrons) with an N-body Hamiltonian formulation. A one-to-one mapping between the EGAM and the BPS is described. The focus is on understanding and predicting the EP redistribution in phase space. We identify here two distinct regimes for the mapping: in the low-drive regime, the BPS mapping with the EGAM is found to be complete, and in the high-drive regime, the EGAM dynamics and the BPS dynamics are found to differ. The transition is described with the presence of a non-negligible frequency chirping, which affects the EGAM but not the BPS, above the identified drive threshold. The difference can be resolved by adding an ad hoc frequency modification to the BPS model. As a main result, the formula for the prediction of the nonlinear width of the velocity redistribution around the resonance velocity is provided. This article is written as the second of a series of articles (the first being Biancalani et al. (J. Plasma Phys., vol. 83 (6), 2017, 725830602)) on the saturation of EGAMs due to wave–particle nonlinearity.

Fully compressible magnetohydrodynamic (MHD) turbulence is investigated in the framework of the multiple-scale direct-interaction approximation. With the aid of the propagators (correlation and Green’s functions), fluctuating fields are solved, and turbulent correlations are estimated in highly compressible turbulence. We focus on the expression of the turbulent electromotive force (EMF). Obliqueness between the mean magnetic field and the mean-density gradient, the mean internal density gradient and the non-equilibrium mean velocity contributes to the EMF in the presence of the density variance, which is ubiquitous in turbulence in strongly variable density flows such as the shock-front region. This density-variance effect is expected to locally enhance the turbulence intensity across the shock front, leading to a fast reconnection.

Starting from expressions in Connor et al. (Phys. Fluids, vol. 31, 1988, p. 577), we derive a one-dimensional tearing equation similar to the approximate equation obtained by Hegna & Callen (Phys. Plasmas, vol. 1, 1994, p. 2308) and Nishimura et al. (Phys. Plasmas, vol. 5, 1998, p. 4292), but for more realistic toroidal equilibria. The intention is to use this approximation to explore the role of steep profiles, bootstrap currents and strong shaping in the vicinity of a separatrix, on the stability of tearing modes which are resonant in the H-mode pedestal region of finite aspect ratio, shaped cross-section tokamaks, e.g. the Joint European Torus (JET). We discuss how this one-dimensional model for tearing modes, which assumes a single poloidal harmonic for the perturbed poloidal flux, compares with a model that includes poloidal coupling Fitzpatrick et al. (Nucl. Fusion, vol. 33, 1993, p. 1533).

Evolving magnetic fields are shown to generically reach a state of fast magnetic reconnection in which magnetic field line connections change and magnetic energy is released at an Alfvénic rate. This occurs even in plasmas with zero resistivity; only the finiteness of the mass of the lightest charged particle, an electron, is required. The speed and prevalence of Alfvénic or fast magnetic reconnection imply that its cause must be contained within the ideal evolution equation for magnetic fields, $\unicode[STIX]{x2202}\boldsymbol{B}/\unicode[STIX]{x2202}t=\unicode[STIX]{x1D735}\times (\boldsymbol{u}\times \boldsymbol{B})$, where $\boldsymbol{u}(\boldsymbol{x},t)$ is the velocity of the magnetic field lines. For a generic $\boldsymbol{u}(\boldsymbol{x},t)$, neighbouring magnetic field lines develop a separation that increases exponentially, as $e^{\unicode[STIX]{x1D70E}(\ell ,t)}$ with $\ell$ the distance along a line. This exponentially enhances the sensitivity of the evolution to non-ideal effects. An analogous effect, the importance of stirring to produce a large-scale flow and enhance mixing, has been recognized by cooks through many millennia, but the importance of the large-scale flow $\boldsymbol{u}$ to reconnection is customarily ignored. In part this is due to the sixty-year focus of recognition theory on two-coordinate models, which eliminate the exponential enhancement that is generic with three coordinates. A simple three-coordinate model is developed, which could be used to address many unanswered questions.

We present a theoretical framework for describing electromagnetic kinetic turbulence in a multi-species, magnetized, pressure-anisotropic plasma. The turbulent fluctuations are assumed to be small compared to the mean field, to be spatially anisotropic with respect to it and to have frequencies small compared to the ion cyclotron frequency. At scales above the ion-Larmor radius, the theory reduces to the pressure-anisotropic generalization of kinetic reduced magnetohydrodynamics (KRMHD) formulated by Kunz et al. (J. Plasma Phys., vol. 81, 2015, 325810501). At scales at and below the ion-Larmor radius, three main objectives are achieved. First, we analyse the linear response of the pressure-anisotropic gyrokinetic system, and show it to be a generalization of previously explored limits. The effects of pressure anisotropy on the stability and collisionless damping of Alfvénic and compressive fluctuations are highlighted, with attention paid to the spectral location and width of the frequency jump that occurs as Alfvén waves transition into kinetic Alfvén waves. Secondly, we derive and discuss a very general gyrokinetic free-energy conservation law, which captures both the KRMHD free-energy conservation at long wavelengths and dual cascades of kinetic Alfvén waves and ion entropy at sub-ion-Larmor scales. We show that non-Maxwellian features in the distribution function change the amount of phase mixing and the efficiency of magnetic stresses, and thus influence the partitioning of free energy amongst the cascade channels. Thirdly, a simple model is used to show that pressure anisotropy, even within the bounds imposed on it by firehose and mirror instabilities, can cause order-of-magnitude variations in the ion-to-electron heating ratio due to the dissipation of Alfvénic turbulence. Our theory provides a foundation for determining how pressure anisotropy affects turbulent fluctuation spectra, the differential heating of particle species and the ratio of parallel and perpendicular phase mixing in space and astrophysical plasmas.

We develop a mean-field theory of compressibility effects in turbulent magnetohydrodynamics and passive scalar transport using the quasi-linear approximation and the spectral $\unicode[STIX]{x1D70F}$-approach. We find that compressibility decreases the $\unicode[STIX]{x1D6FC}$ effect and the turbulent magnetic diffusivity both at small and large magnetic Reynolds numbers, $Rm$. Similarly, compressibility decreases the turbulent diffusivity for passive scalars both at small and large Péclet numbers, $Pe$. On the other hand, compressibility does not affect the effective pumping velocity of the magnetic field for large $Rm$, but it decreases it for small $Rm$. Density stratification causes turbulent pumping of passive scalars, but it is found to become weaker with increasing compressibility. No such pumping effect exists for magnetic fields. However, compressibility results in a new passive scalar pumping effect from regions of low to high turbulent intensity both for small and large Péclet numbers. It can be interpreted as compressible turbophoresis of non-inertial particles and gaseous admixtures, while the classical turbophoresis effect exists only for inertial particles and causes them to be pumped to regions with lower turbulent intensity.

We explore the growth of large-scale magnetic fields in a shear flow, due to helicity fluctuations with a finite correlation time, through a study of the Kraichnan–Moffatt model of zero-mean stochastic fluctuations of the $\unicode[STIX]{x1D6FC}$ parameter of dynamo theory. We derive a linear integro-differential equation for the evolution of the large-scale magnetic field, using the first-order smoothing approximation and the Galilean invariance of the $\unicode[STIX]{x1D6FC}$-statistics. This enables construction of a model that is non-perturbative in the shearing rate $S$ and the $\unicode[STIX]{x1D6FC}$-correlation time $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$. After a brief review of the salient features of the exactly solvable white-noise limit, we consider the case of small but non-zero $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FC}}$. When the large-scale magnetic field varies slowly, the evolution is governed by a partial differential equation. We present modal solutions and conditions for the exponential growth rate of the large-scale magnetic field, whose drivers are the Kraichnan diffusivity, Moffatt drift, shear and a non-zero correlation time. Of particular interest is dynamo action when the $\unicode[STIX]{x1D6FC}$-fluctuations are weak; i.e. when the Kraichnan diffusivity is positive. We show that in the absence of Moffatt drift, shear does not give rise to growing solutions. But shear and Moffatt drift acting together can drive large-scale dynamo action with growth rate $\unicode[STIX]{x1D6FE}\propto |S|$.

A family of Lorentz invariant scalar functions of the magnetic field is defined in an ideal relativistic plasma. These invariants are advected by the plasma fluid motion and play the role of the potential magnetic field introduced by Hide in (Ann. Geophys., vol. 1, 1983, 59) along the lines of Ertel’s theorem. From these invariants we recover the Cauchy conditions for the magnetic field components in the mapping from Eulerian to Lagrangian variables. In addition, the adopted procedure allows us to formulate, in a Lorentz invariant form, the Alfvén theorem for the conservation of the magnetic flux through a surface comoving with the plasma.

Reconnection outflows have been under intense recent scrutiny, from in situ observations and from simulations. These regions are host to a variety of instabilities and intense energy exchanges, often even superior to the main reconnection site. We report here a number of results drawn from an investigation of simulations. First, the outflows are observed to become unstable to drift instabilities. Second, these instabilities lead to the formation of secondary reconnection sites. Third, the secondary processes are responsible for large energy exchanges and particle energization. Finally, the particle distribution function are modified to become non-Maxwellian and include multiple interpenetrating populations.

The homogeneous dynamo effect is at the root of magnetic field generation in cosmic bodies, including planets, stars and galaxies. While the underlying theory had increasingly flourished since the middle of the 20th century, hydromagnetic dynamos were not realized in the laboratory until 1999. On 11 November 1999, this situation changed with the first observation of a kinematic dynamo in the Riga experiment. Since that time, a series of experimental campaigns has provided a wealth of data on the kinematic and the saturated regime. This paper is intended to give a comprehensive survey about these experiments, to summarize their main results and to compare them with numerical simulations.

There has been a growing interest, over the past few years, on understanding the effect on radio frequency waves due to turbulence in the scrape-off layer of tokamak plasmas. While the far scrape-off layer density width is of the order of centimetres in contemporary tokamaks, in ITER (International Thermonuclear Experimental Reactor), and in future fusion reactors, the corresponding width will be of the order of tens of centimetres. As such, this could impact the spectral properties of the waves and, consequently, the transport of wave energy and momentum to the core plasma. The turbulence in the scrape-off layer spans a broad range of spatial scales and includes blobs and filaments that are elongated along the magnetic field lines. The propagation of radio frequency waves through this tenuous plasma is given by Maxwell’s equations. The characteristic properties of the plasma appear as a permittivity tensor in the expression for the current in Ampere’s equation. This paper develops a formalism for expressing the permittivity of a turbulent plasma using the homogenization technique. This technique has been extensively used to express the dielectric properties of composite materials that are spatially inhomogeneous, for example, due to the presence of micro-structures. In a similar vein, the turbulent plasma in the scrape-off layer is spatially inhomogeneous and can be considered as a composite material in which the micro-structures are filaments and blobs. The classical homogenization technique is not appropriate for the magnetized plasma in the scrape-off layer, as the radio frequency waves span a broad range of wavelengths and frequencies – from tens of megahertz to hundreds of gigahertz. The formalism in this paper makes use of the Fourier space components of the electric and magnetic fields of the radio frequency waves for the scattered fields and fields inside the filaments and blobs. These are the eigenvectors of the dispersion matrix which, using the Green’s function approach, lead to a homogenized dielectric tensor.

The effect of electrostatic microturbulence on fast particles rapidly decreases at high energy, but can be significant at moderate energy. Previous studies found that, in addition to changes in the energetic particle density, this results in non-trivial changes to the equilibrium velocity distribution. These effects have implications for plasma heating and the stability of Alfvén eigenmodes, but make multiscale simulations much more difficult without further approximations. Here, several related analytic model distribution functions are derived from first principles. A single dimensionless parameter characterizes the relative strength of turbulence relative to collisions, and this parameter appears as an exponent in the model distribution functions. Even the most simple of these models reproduces key features of the numerical phase-space transport solution and provides a useful a priori heuristic for determining how strong the effect of turbulence is on the redistribution of energetic particles in toroidal plasmas.