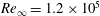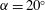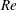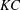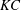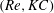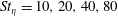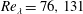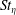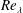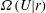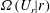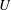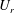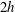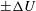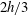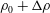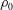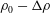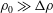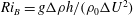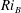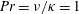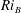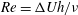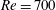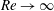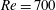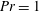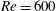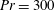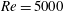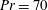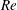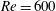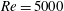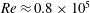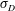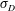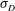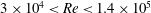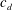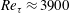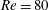We present the linear stability properties and nonlinear evolution of two-dimensional plane Couette flow for a statically stable Boussinesq three-layer fluid of total depth 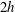 $2h$ between two horizontal plates driven at constant velocity
$2h$ between two horizontal plates driven at constant velocity 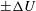 $\pm \unicode[STIX]{x0394}U$. Initially the three layers have equal depth
$\pm \unicode[STIX]{x0394}U$. Initially the three layers have equal depth 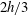 $2h/3$ and densities
$2h/3$ and densities 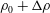 $\unicode[STIX]{x1D70C}_{0}+\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$,
$\unicode[STIX]{x1D70C}_{0}+\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$, 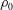 $\unicode[STIX]{x1D70C}_{0}$ and
$\unicode[STIX]{x1D70C}_{0}$ and 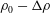 $\unicode[STIX]{x1D70C}_{0}-\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$, such that
$\unicode[STIX]{x1D70C}_{0}-\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$, such that 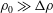 $\unicode[STIX]{x1D70C}_{0}\gg \unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$. At finite Reynolds and Prandtl number, we demonstrate that this flow is susceptible to two distinct primary linear instabilities for sufficiently large bulk Richardson number
$\unicode[STIX]{x1D70C}_{0}\gg \unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$. At finite Reynolds and Prandtl number, we demonstrate that this flow is susceptible to two distinct primary linear instabilities for sufficiently large bulk Richardson number 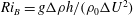 $Ri_{B}=g\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}h/(\unicode[STIX]{x1D70C}_{0}\unicode[STIX]{x0394}U^{2})$. For a given bulk Richardson number
$Ri_{B}=g\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}h/(\unicode[STIX]{x1D70C}_{0}\unicode[STIX]{x0394}U^{2})$. For a given bulk Richardson number 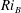 $Ri_{B}$, the zero phase speed ‘Taylor’ instability is always predicted to have the largest growth rate and to be an inherently two-dimensional instability. An inherently viscous instability, reminiscent of the ‘Holmboe’ instability, is also predicted to have a non-zero growth rate. For flows with Prandtl number
$Ri_{B}$, the zero phase speed ‘Taylor’ instability is always predicted to have the largest growth rate and to be an inherently two-dimensional instability. An inherently viscous instability, reminiscent of the ‘Holmboe’ instability, is also predicted to have a non-zero growth rate. For flows with Prandtl number 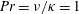 $Pr=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D705}=1$, where
$Pr=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D705}=1$, where  $\unicode[STIX]{x1D708}$ is the kinematic viscosity, and
$\unicode[STIX]{x1D708}$ is the kinematic viscosity, and  $\unicode[STIX]{x1D705}$ is the diffusivity of the density distribution, we find that the most unstable Taylor instability, maximized across wavenumber and
$\unicode[STIX]{x1D705}$ is the diffusivity of the density distribution, we find that the most unstable Taylor instability, maximized across wavenumber and 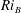 $Ri_{B}$, has a (linear) growth rate which is a non-monotonic function of Reynolds number
$Ri_{B}$, has a (linear) growth rate which is a non-monotonic function of Reynolds number 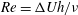 $Re=\unicode[STIX]{x0394}Uh/\unicode[STIX]{x1D708}$, with a global maximum at
$Re=\unicode[STIX]{x0394}Uh/\unicode[STIX]{x1D708}$, with a global maximum at 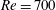 $Re=700$ over 50 % larger than the growth rate as
$Re=700$ over 50 % larger than the growth rate as 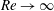 $Re\rightarrow \infty$. In a fully nonlinear evolution of the flows with
$Re\rightarrow \infty$. In a fully nonlinear evolution of the flows with 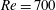 $Re=700$ and
$Re=700$ and 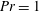 $Pr=1$, the two interfaces between the three density layers diffuse more rapidly than the underlying instabilities can grow from small amplitude. Therefore, we investigate numerically the nonlinear evolution of the flow at
$Pr=1$, the two interfaces between the three density layers diffuse more rapidly than the underlying instabilities can grow from small amplitude. Therefore, we investigate numerically the nonlinear evolution of the flow at 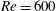 $Re=600$ and
$Re=600$ and 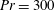 $Pr=300$, and at
$Pr=300$, and at 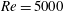 $Re=5000$ and
$Re=5000$ and 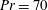 $Pr=70$ in two-dimensional domains with streamwise extent equal to two wavelengths of the Taylor instability with the largest growth rate. At both sets of parameter values, the primary Taylor instability undergoes a period of identifiable exponential ‘linear’ growth. However, we demonstrate that, unlike the so-called ‘Kelvin–Helmholtz’ instability that it superficially resembles, the Taylor instability’s finite-amplitude state of an elliptical vortex in the middle layer appears not to saturate into a quasiequilibrium state, but is rapidly destroyed by the background shear. The decay process reveals
$Pr=70$ in two-dimensional domains with streamwise extent equal to two wavelengths of the Taylor instability with the largest growth rate. At both sets of parameter values, the primary Taylor instability undergoes a period of identifiable exponential ‘linear’ growth. However, we demonstrate that, unlike the so-called ‘Kelvin–Helmholtz’ instability that it superficially resembles, the Taylor instability’s finite-amplitude state of an elliptical vortex in the middle layer appears not to saturate into a quasiequilibrium state, but is rapidly destroyed by the background shear. The decay process reveals 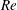 $Re$-dependent secondary processes. For the
$Re$-dependent secondary processes. For the 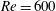 $Re=600$ simulation, this decay allows the development to finite amplitude of the co-existing primary ‘viscous Holmboe wave instability’, which has a substantially smaller linear growth rate. For the
$Re=600$ simulation, this decay allows the development to finite amplitude of the co-existing primary ‘viscous Holmboe wave instability’, which has a substantially smaller linear growth rate. For the 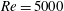 $Re=5000$ simulation, the Taylor instability decay induces a non-trivial modification of the mean velocity and density distributions, which nonlinearly develops into more classical finite-amplitude Holmboe waves. In both cases, the saturated nonlinear Holmboe waves are robust and long-lived in two-dimensional flow.
$Re=5000$ simulation, the Taylor instability decay induces a non-trivial modification of the mean velocity and density distributions, which nonlinearly develops into more classical finite-amplitude Holmboe waves. In both cases, the saturated nonlinear Holmboe waves are robust and long-lived in two-dimensional flow.