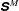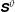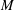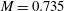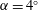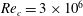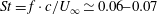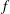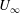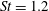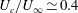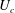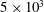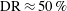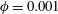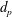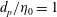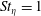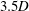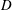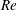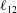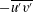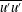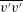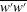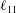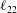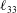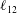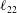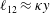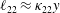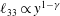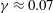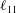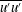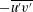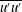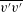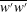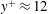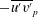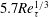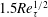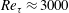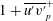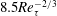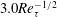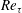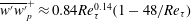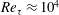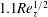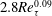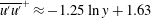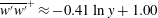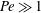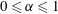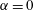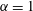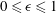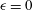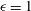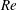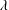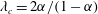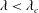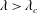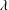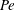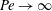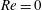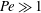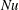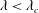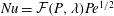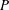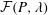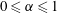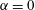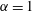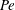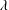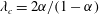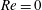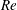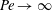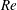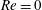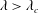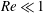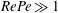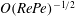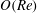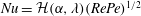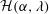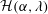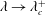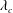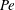We analyse the singular effects of weak inertia on the heat (or equivalently mass) transport problem from drops in linear shearing flows. For small spherical drops embedded in hyperbolic planar linear flows, which constitute a one-parameter family (the parameter being  $\unicode[STIX]{x1D6FC}$ with
$\unicode[STIX]{x1D6FC}$ with 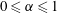 $0\leqslant \unicode[STIX]{x1D6FC}\leqslant 1$, and whose extremal members are simple shear (
$0\leqslant \unicode[STIX]{x1D6FC}\leqslant 1$, and whose extremal members are simple shear (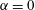 $\unicode[STIX]{x1D6FC}=0$) and planar extension (
$\unicode[STIX]{x1D6FC}=0$) and planar extension (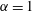 $\unicode[STIX]{x1D6FC}=1$)), there are two distinct regimes for scalar (heat or mass) transport at large Péclet numbers (
$\unicode[STIX]{x1D6FC}=1$)), there are two distinct regimes for scalar (heat or mass) transport at large Péclet numbers (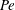 $Pe$) depending on the exterior streamline topology (Krishnamurthy & Subramanian, J. Fluid Mech., vol. 850, 2018, pp. 439–483). When the drop-to-medium viscosity ratio (
$Pe$) depending on the exterior streamline topology (Krishnamurthy & Subramanian, J. Fluid Mech., vol. 850, 2018, pp. 439–483). When the drop-to-medium viscosity ratio (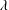 $\unicode[STIX]{x1D706}$) is larger than a critical value,
$\unicode[STIX]{x1D706}$) is larger than a critical value, 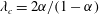 $\unicode[STIX]{x1D706}_{c}=2\unicode[STIX]{x1D6FC}/(1-\unicode[STIX]{x1D6FC})$, the drop is surrounded by a region of closed streamlines in the inertialess limit (
$\unicode[STIX]{x1D706}_{c}=2\unicode[STIX]{x1D6FC}/(1-\unicode[STIX]{x1D6FC})$, the drop is surrounded by a region of closed streamlines in the inertialess limit (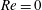 $Re=0$,
$Re=0$, 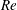 $Re$ being the drop Reynolds number). Convection is incapable of transporting heat away on account of the near-field closed streamline topology, and the transport remains diffusion limited even for
$Re$ being the drop Reynolds number). Convection is incapable of transporting heat away on account of the near-field closed streamline topology, and the transport remains diffusion limited even for 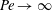 $Pe\rightarrow \infty$. However, weak inertia breaks open the closed streamline region, giving way to finite-
$Pe\rightarrow \infty$. However, weak inertia breaks open the closed streamline region, giving way to finite-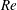 $Re$ spiralling streamlines and convectively enhanced transport. For
$Re$ spiralling streamlines and convectively enhanced transport. For 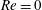 $Re=0$ the closed streamlines on the drop surface, for
$Re=0$ the closed streamlines on the drop surface, for 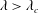 $\unicode[STIX]{x1D706}>\unicode[STIX]{x1D706}_{c}$, are Jeffery orbits, a terminology originally used to describe the trajectories of an axisymmetric rigid particle in a simple shear flow. Based on this identification, a novel boundary layer analysis that employs a surface-flow-aligned non-orthogonal coordinate system, is used to solve the transport problem in the dual asymptotic limit
$\unicode[STIX]{x1D706}>\unicode[STIX]{x1D706}_{c}$, are Jeffery orbits, a terminology originally used to describe the trajectories of an axisymmetric rigid particle in a simple shear flow. Based on this identification, a novel boundary layer analysis that employs a surface-flow-aligned non-orthogonal coordinate system, is used to solve the transport problem in the dual asymptotic limit 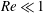 $Re\ll 1$,
$Re\ll 1$, 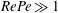 $RePe\gg 1$, corresponding to the regime where inertial convection balances diffusion in an
$RePe\gg 1$, corresponding to the regime where inertial convection balances diffusion in an 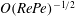 $O(RePe)^{-1/2}$ boundary layer. Further, the separation of time scales in the aforementioned limit, between rapid convection due to the Stokesian velocity field and the slower convection by the
$O(RePe)^{-1/2}$ boundary layer. Further, the separation of time scales in the aforementioned limit, between rapid convection due to the Stokesian velocity field and the slower convection by the 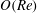 $O(Re)$ inertial velocity field, allows one to average the convection–diffusion equation over the phase of the Stokesian surface streamlines (Jeffery orbits), allowing a simplification of the original three-dimensional non-axisymmetric transport problem to a form resembling a much simpler axisymmetric one. A self-similar ansatz then leads to the boundary layer temperature field, and the resulting Nusselt number is given by
$O(Re)$ inertial velocity field, allows one to average the convection–diffusion equation over the phase of the Stokesian surface streamlines (Jeffery orbits), allowing a simplification of the original three-dimensional non-axisymmetric transport problem to a form resembling a much simpler axisymmetric one. A self-similar ansatz then leads to the boundary layer temperature field, and the resulting Nusselt number is given by 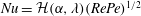 $Nu={\mathcal{H}}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D706})(RePe)^{1/2}$ with
$Nu={\mathcal{H}}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D706})(RePe)^{1/2}$ with 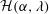 ${\mathcal{H}}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D706})$ given in terms of a one-dimensional integral; the prefactor
${\mathcal{H}}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D706})$ given in terms of a one-dimensional integral; the prefactor 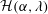 ${\mathcal{H}}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D706})$ diverges for
${\mathcal{H}}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D706})$ diverges for 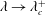 $\unicode[STIX]{x1D706}\rightarrow \unicode[STIX]{x1D706}_{c}^{+}$ due to assumptions underlying the Jeffery-orbit-averaged analysis breaking down. Although the separation of time scales necessary for the validity of the analysis no longer exists in the transition regime (
$\unicode[STIX]{x1D706}\rightarrow \unicode[STIX]{x1D706}_{c}^{+}$ due to assumptions underlying the Jeffery-orbit-averaged analysis breaking down. Although the separation of time scales necessary for the validity of the analysis no longer exists in the transition regime (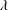 $\unicode[STIX]{x1D706}$ in the neighbourhood of
$\unicode[STIX]{x1D706}$ in the neighbourhood of 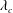 $\unicode[STIX]{x1D706}_{c}$), scaling arguments nevertheless highlight the manner in which the Nusselt number function connects smoothly across the open and closed streamline regimes for any finite
$\unicode[STIX]{x1D706}_{c}$), scaling arguments nevertheless highlight the manner in which the Nusselt number function connects smoothly across the open and closed streamline regimes for any finite 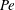 $Pe$.
$Pe$.