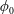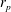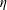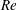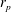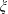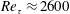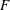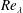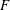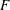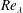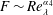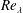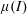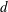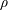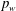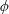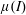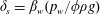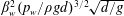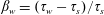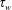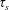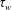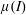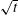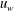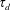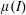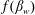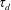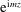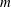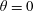JFM Papers
Thermocapillary migration of droplets under molecular and gravitational forces
-
- Published online by Cambridge University Press:
- 17 May 2018, pp. 1-27
-
- Article
- Export citation
Numerical study of turbulent separation bubbles with varying pressure gradient and Reynolds number
-
- Published online by Cambridge University Press:
- 17 May 2018, pp. 28-70
-
- Article
- Export citation
Capillary interactions between dynamically forced particles adsorbed at a planar interface and on a bubble
-
- Published online by Cambridge University Press:
- 21 May 2018, pp. 71-92
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Flow-induced vibration control of a circular cylinder using rotational oscillation feedback
-
- Published online by Cambridge University Press:
- 21 May 2018, pp. 93-118
-
- Article
- Export citation
An experimental study of the motion of a light sphere in a rotating viscous fluid
-
- Published online by Cambridge University Press:
- 21 May 2018, pp. 119-133
-
- Article
- Export citation
Monodisperse particle-laden exchange flows in a vertical duct
-
- Published online by Cambridge University Press:
- 21 May 2018, pp. 134-160
-
- Article
- Export citation
Large coherence of spanwise velocity in turbulent boundary layers
-
- Published online by Cambridge University Press:
- 21 May 2018, pp. 161-185
-
- Article
- Export citation
Laboratory-scale swash flows generated by a non-breaking solitary wave on a steep slope
-
- Published online by Cambridge University Press:
- 21 May 2018, pp. 186-227
-
- Article
- Export citation
Advection and diffusion in a chemically induced compressible flow
-
- Published online by Cambridge University Press:
- 21 May 2018, pp. 228-243
-
- Article
- Export citation
Reappraisal of the velocity derivative flatness factor in various turbulent flows
-
- Published online by Cambridge University Press:
- 21 May 2018, pp. 244-265
-
- Article
- Export citation
Non-ideal oblique shock waves
-
- Published online by Cambridge University Press:
- 21 May 2018, pp. 266-285
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The effects of fluid transport on the creation of a dense cluster of activated fractures in a porous medium
-
- Published online by Cambridge University Press:
- 21 May 2018, pp. 286-328
-
- Article
- Export citation
Boundary control in computational haemodynamics
-
- Published online by Cambridge University Press:
- 21 May 2018, pp. 329-364
-
- Article
- Export citation
A note on Stokes’ problem in dense granular media using the
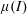 $\unicode[STIX]{x1D707}(I)$-rheology
$\unicode[STIX]{x1D707}(I)$-rheology
-
- Published online by Cambridge University Press:
- 23 May 2018, pp. 365-385
-
- Article
- Export citation
Swimming performance, resonance and shape evolution in heaving flexible panels
-
- Published online by Cambridge University Press:
- 23 May 2018, pp. 386-416
-
- Article
-
- You have access
- HTML
- Export citation
Stimulated generation: extraction of energy from balanced flow by near-inertial waves
-
- Published online by Cambridge University Press:
- 23 May 2018, pp. 417-451
-
- Article
- Export citation
Direct numerical simulation of heat transfer from a cylinder immersed in the production and decay regions of grid-element turbulence
-
- Published online by Cambridge University Press:
- 23 May 2018, pp. 452-488
-
- Article
- Export citation
Effects of surface tension on a floating body in two dimensions
-
- Published online by Cambridge University Press:
- 23 May 2018, pp. 489-519
-
- Article
- Export citation
Fluid particle dynamics and the non-local origin of the Reynolds shear stress
-
- Published online by Cambridge University Press:
- 23 May 2018, pp. 520-551
-
- Article
- Export citation
Influence of permeable beds on hydraulically macro-rough flow
-
- Published online by Cambridge University Press:
- 25 May 2018, pp. 552-590
-
- Article
- Export citation