1 Introduction
The design of aerodynamic devices and systems often requires special care to account for shock wave formation and related losses. Complex patterns of oblique shock waves can indeed be found in diverse applications including, just to mention a few, engine intakes of high-speed aircrafts and rockets, supersonic nozzle outflows, under-expanded jets and highly loaded turbomachinery stages. The variation of the thermodynamic and kinematic quantities across the shock wave is determined by the Mach number of the flow ahead of the shock, relative to the shock front itself, in dilute-gas flows to which the theory of perfect gases can be reasonably applied. If instead the thermodynamic states of the fluid cannot be accurately described by means of the perfect-gas model, a more or less noticeable dependence on the pre-shock thermodynamic state, say the values of the pre-shock temperature and pressure, is also observed. Most of the features of shock waves and, more in general, the nonlinear dynamics of compressible fluids, depends on the evolution of the speed of sound
![]() $c=\sqrt{(\unicode[STIX]{x2202}P/\unicode[STIX]{x2202}\unicode[STIX]{x1D70C})_{s}}$
along isentropic transformations, where
$c=\sqrt{(\unicode[STIX]{x2202}P/\unicode[STIX]{x2202}\unicode[STIX]{x1D70C})_{s}}$
along isentropic transformations, where
![]() $P$
,
$P$
,
![]() $\unicode[STIX]{x1D70C}$
and
$\unicode[STIX]{x1D70C}$
and
![]() $s$
denote the fluid pressure, density and entropy, respectively. Following common practice, the sound-speed isentropic variation is expressed in non-dimensional form by the parameter
$s$
denote the fluid pressure, density and entropy, respectively. Following common practice, the sound-speed isentropic variation is expressed in non-dimensional form by the parameter
![]() $\unicode[STIX]{x1D6E4}$
,
$\unicode[STIX]{x1D6E4}$
,
referred to as the fundamental derivative of gas dynamics (Thompson Reference Thompson1971). For perfect gases,
![]() $\unicode[STIX]{x1D6E4}=(\unicode[STIX]{x1D6FE}+1)/2>1$
, where
$\unicode[STIX]{x1D6E4}=(\unicode[STIX]{x1D6FE}+1)/2>1$
, where
![]() $\unicode[STIX]{x1D6FE}>1$
is the ratio of the specific heats. Therefore, in a dilute gas, the speed of sound increases upon isentropic compression. However, near to the liquid–vapour phase transition and critical point, the interaction between attractive and repulsive intermolecular forces can possibly result in a decrease in the speed of sound across isentropic compressive processes, see Colonna & Guardone (Reference Colonna and Guardone2006) and Harinck, Guardone & Colonna (Reference Harinck, Guardone and Colonna2009). This is expected to occur in fluids with large heat capacities, corresponding to a sufficient level of molecular complexity (Lambrakis & Thompson Reference Lambrakis and Thompson1972; Thompson & Lambrakis Reference Thompson and Lambrakis1973). The gas dynamics associated with thermodynamic states featuring
$\unicode[STIX]{x1D6FE}>1$
is the ratio of the specific heats. Therefore, in a dilute gas, the speed of sound increases upon isentropic compression. However, near to the liquid–vapour phase transition and critical point, the interaction between attractive and repulsive intermolecular forces can possibly result in a decrease in the speed of sound across isentropic compressive processes, see Colonna & Guardone (Reference Colonna and Guardone2006) and Harinck, Guardone & Colonna (Reference Harinck, Guardone and Colonna2009). This is expected to occur in fluids with large heat capacities, corresponding to a sufficient level of molecular complexity (Lambrakis & Thompson Reference Lambrakis and Thompson1972; Thompson & Lambrakis Reference Thompson and Lambrakis1973). The gas dynamics associated with thermodynamic states featuring
![]() $\unicode[STIX]{x1D6E4}<1$
may significantly differ from its ideal-gas counterpart, thus justifying the use of expressions such as non-ideal effects in reference to the related peculiarities. These include, e.g. the decrease of the flow Mach number along supersonic expansions in fluids exhibiting
$\unicode[STIX]{x1D6E4}<1$
may significantly differ from its ideal-gas counterpart, thus justifying the use of expressions such as non-ideal effects in reference to the related peculiarities. These include, e.g. the decrease of the flow Mach number along supersonic expansions in fluids exhibiting
![]() $0<\unicode[STIX]{x1D6E4}<1$
(Cramer & Best Reference Cramer and Best1991) and so-called non-classical phenomena that are caused by negative nonlinearities (
$0<\unicode[STIX]{x1D6E4}<1$
(Cramer & Best Reference Cramer and Best1991) and so-called non-classical phenomena that are caused by negative nonlinearities (
![]() $\unicode[STIX]{x1D6E4}<0$
) or mixed nonlinearities (
$\unicode[STIX]{x1D6E4}<0$
) or mixed nonlinearities (
![]() $\unicode[STIX]{x1D6E4}$
changing its sign), the most striking example being the admissibility of expansion shocks and composite waves. The reader is referred to Cramer & Kluwick (Reference Cramer and Kluwick1984), Menikoff & Plohr (Reference Menikoff and Plohr1989) and Kluwick (Reference Kluwick2001) for reviews on non-classical gas dynamics. It must be noticed, however, that experimental evidence of negative nonlinearities is still missing at present, thus leaving the existence of non-classical phenomena an open question in fluid mechanics. In this respect, recent advancements indicate the possibility of observing negative nonlinearities in common substances (other than Bethe–Zel’dovich–Thompson (BZT) fluids) due to critical-point anomalies (see Nannan, Guardone & Colonna Reference Nannan, Guardone and Colonna2014; Nannan et al.
Reference Nannan, Sirianni, Mathijssen, Guardone and Colonna2016).
$\unicode[STIX]{x1D6E4}$
changing its sign), the most striking example being the admissibility of expansion shocks and composite waves. The reader is referred to Cramer & Kluwick (Reference Cramer and Kluwick1984), Menikoff & Plohr (Reference Menikoff and Plohr1989) and Kluwick (Reference Kluwick2001) for reviews on non-classical gas dynamics. It must be noticed, however, that experimental evidence of negative nonlinearities is still missing at present, thus leaving the existence of non-classical phenomena an open question in fluid mechanics. In this respect, recent advancements indicate the possibility of observing negative nonlinearities in common substances (other than Bethe–Zel’dovich–Thompson (BZT) fluids) due to critical-point anomalies (see Nannan, Guardone & Colonna Reference Nannan, Guardone and Colonna2014; Nannan et al.
Reference Nannan, Sirianni, Mathijssen, Guardone and Colonna2016).
On the other hand, well-established and accurate thermodynamic models predict that several fluids currently employed in industrial processes feature
![]() $0<\unicode[STIX]{x1D6E4}<1$
in the single-phase vapour region, prominent examples being hydrocarbons, fluorocarbons and siloxanes used as working fluids in organic Rankine cycle (ORC) power systems. Related phenomena of practical interest include the aforementioned decrease of the flow Mach number in supersonic expansions (Cramer & Best Reference Cramer and Best1991), the non-ideal evolution of the Mach number in diabatic supersonic nozzle flows (Schnerr & Leidner Reference Schnerr and Leidner1991) and the increase of the flow Mach number across oblique shock waves (Gori, Vimercati & Guardone Reference Gori, Vimercati and Guardone2017), which is the focus of the present investigation. This peculiar kind of oblique shock waves, namely those characterized by a larger flow Mach number in the post-shock state than in the pre-shock state, will be referred to as non-ideal oblique shock waves. Following the analysis of isentropic compressions by Cramer & Best (Reference Cramer and Best1991), it is straightforward to demonstrate that in the limit of shock wave of vanishing intensity, the Mach number can possibly increase across a compressions wave if
$0<\unicode[STIX]{x1D6E4}<1$
in the single-phase vapour region, prominent examples being hydrocarbons, fluorocarbons and siloxanes used as working fluids in organic Rankine cycle (ORC) power systems. Related phenomena of practical interest include the aforementioned decrease of the flow Mach number in supersonic expansions (Cramer & Best Reference Cramer and Best1991), the non-ideal evolution of the Mach number in diabatic supersonic nozzle flows (Schnerr & Leidner Reference Schnerr and Leidner1991) and the increase of the flow Mach number across oblique shock waves (Gori, Vimercati & Guardone Reference Gori, Vimercati and Guardone2017), which is the focus of the present investigation. This peculiar kind of oblique shock waves, namely those characterized by a larger flow Mach number in the post-shock state than in the pre-shock state, will be referred to as non-ideal oblique shock waves. Following the analysis of isentropic compressions by Cramer & Best (Reference Cramer and Best1991), it is straightforward to demonstrate that in the limit of shock wave of vanishing intensity, the Mach number can possibly increase across a compressions wave if
![]() $\unicode[STIX]{x1D6E4}<1$
. The goal of the present paper is to investigate classical compression shock waves of finite amplitude to complement the previous study of Gori et al. (Reference Gori, Vimercati and Guardone2017), where non-ideal oblique shock waves are studied using the simple van der Waals model. In particular, the precise conditions allowing for non-ideal oblique shocks to occur in single-phase vapour flows of fluids exhibiting positive nonlinearity are examined here. A convenient procedure is detailed which allows to determine the existence domain, in terms of pre-shock state properties, of non-ideal oblique shock waves. The non-ideal increase of the flow Mach number across oblique shocks is arguably relevant in applications where oblique shock waves are either intentionally formed (e.g. engine intake ramps) or a by-product of the supersonic flow expansion (e.g. fish-tail shocks in turbine nozzle vanes, over/under-expanded jet from a nozzle exit).
$\unicode[STIX]{x1D6E4}<1$
. The goal of the present paper is to investigate classical compression shock waves of finite amplitude to complement the previous study of Gori et al. (Reference Gori, Vimercati and Guardone2017), where non-ideal oblique shock waves are studied using the simple van der Waals model. In particular, the precise conditions allowing for non-ideal oblique shocks to occur in single-phase vapour flows of fluids exhibiting positive nonlinearity are examined here. A convenient procedure is detailed which allows to determine the existence domain, in terms of pre-shock state properties, of non-ideal oblique shock waves. The non-ideal increase of the flow Mach number across oblique shocks is arguably relevant in applications where oblique shock waves are either intentionally formed (e.g. engine intake ramps) or a by-product of the supersonic flow expansion (e.g. fish-tail shocks in turbine nozzle vanes, over/under-expanded jet from a nozzle exit).
The present work is organized as follows. In § 2, the basics of shock waves are reviewed and the properties of shock curves in classical gas dynamics are discussed. The theoretical framework for the investigation of non-ideal oblique shocks is outlined. Section 3 describes the computation of the existence domain, in terms of pre-shock thermodynamic quantities and Mach number, leading to non-ideal oblique shocks. Results are presented for different substances of practical interest. Section 4 provides the concluding remarks.
2 Oblique shocks in the non-ideal gas dynamic regime
The present section recalls the theory of oblique shock wave starting from the integral relation between the states across the shock and the admissibility conditions. The properties of shock curves are analysed within the classical gas dynamic context (
![]() $\unicode[STIX]{x1D6E4}>0$
), providing the theoretical justification for the occurrence of non-ideal oblique shocks.
$\unicode[STIX]{x1D6E4}>0$
), providing the theoretical justification for the occurrence of non-ideal oblique shocks.
2.1 Jump relations and shock admissibility
We assume the shock wave to be a vanishing-thickness layer separating two regions of thermodynamic-equilibrium states within a non-reacting substance (see, e.g. Zel’dovich Reference Zel’dovich1946; Landau & Lifshitz Reference Landau and Lifshitz1987). In a shock-attached reference frame, the laws of conservation of mass, momentum and energy across the shock front, namely the well-known Rankine–Hugoniot relations for three-dimensional flows, locally assume the form
is the mass flux across the discontinuity. Equation (2.3a
), known as the Hugoniot relation, determines the set, termed the Hugoniot locus, of thermodynamic states that can be connected by means of a shock wave. In the
![]() $P$
–
$P$
–
![]() $v$
plane, the Hugoniot locus is commonly referred to as the shock adiabat, and the straight line defined by relation (2.3b
) as the Rayleigh line.
$v$
plane, the Hugoniot locus is commonly referred to as the shock adiabat, and the straight line defined by relation (2.3b
) as the Rayleigh line.
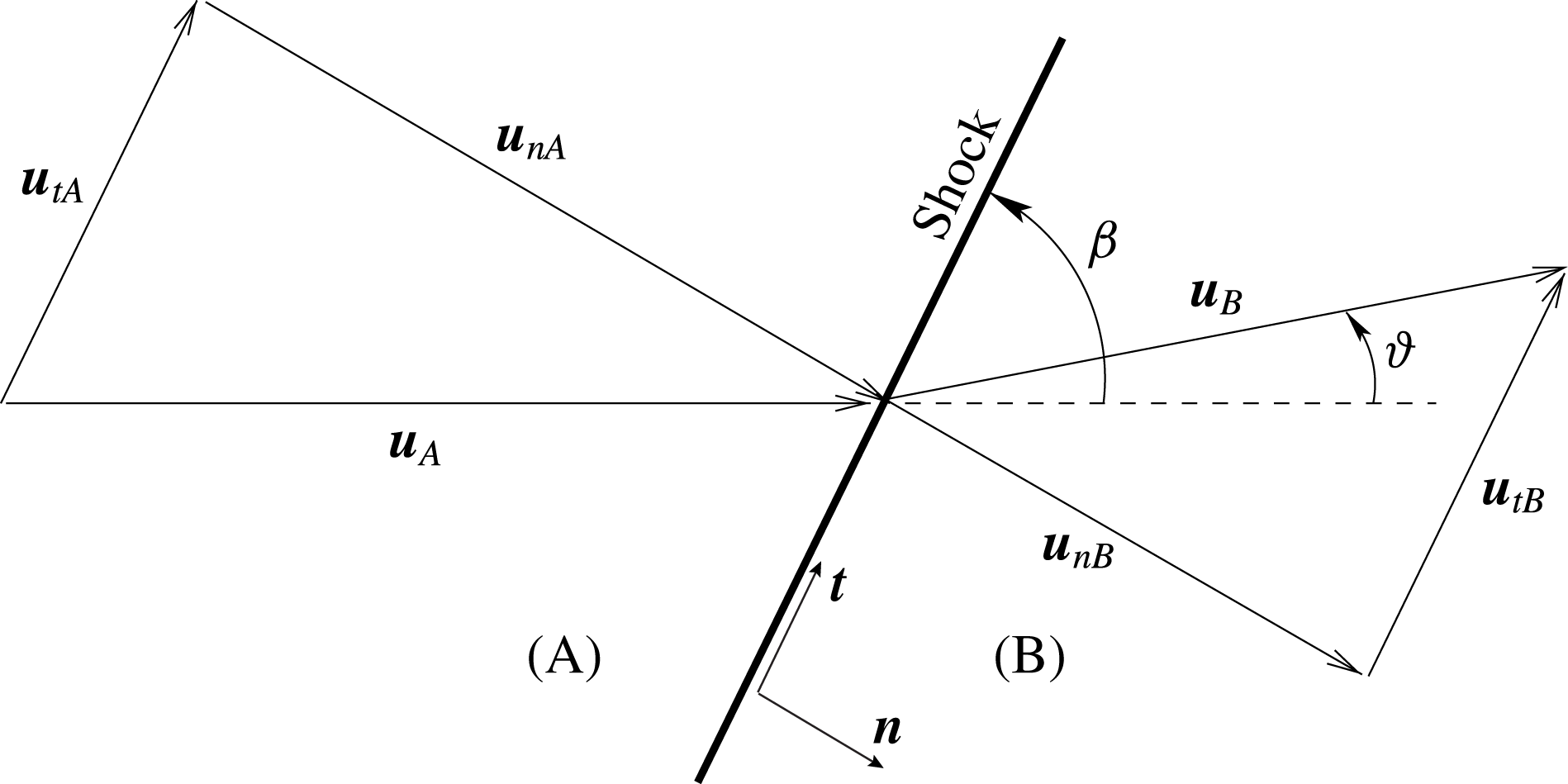
Figure 1. Qualitative illustration of the local shock front. States A and B represent the pre-shock and post-shock states, respectively. For ease of representation, the shock-attached reference frame is such that the plane spanned by unit vectors
![]() $\boldsymbol{n}$
and
$\boldsymbol{n}$
and
![]() $\boldsymbol{t}$
(normal and tangent to the shock front, respectively) contains the fluid velocity
$\boldsymbol{t}$
(normal and tangent to the shock front, respectively) contains the fluid velocity
![]() $\boldsymbol{u}$
. The angles
$\boldsymbol{u}$
. The angles
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
![]() $\unicode[STIX]{x1D703}$
are the shock angle and flow deviation angle, respectively, both computed with respect to the pre-shock flow direction.
$\unicode[STIX]{x1D703}$
are the shock angle and flow deviation angle, respectively, both computed with respect to the pre-shock flow direction.
The Rankine–Hugoniot relations are not sufficient to isolate physically realizable shock solutions. These are selected by enforcing extra conditions accounting for physical effects that are not modelled in the simplified governing equations (viz. the limit of vanishing viscosity and heat conduction). Because the second law of thermodynamics requires that entropy does not decrease, (2.1) must be extended to include
Further admissibility conditions stem from mechanical stability requirements. In order that the shock front be stable against one-dimensional perturbations of the normal flow, the well-known speed-ordering relation
must be satisfied along the shock front, where
![]() $M_{\boldsymbol{n}}=u_{\boldsymbol{n}}/c$
denotes the normal Mach number (Lax Reference Lax1957). The conditions for stability with respect to multidimensional perturbations can be conveniently related to geometric properties of the shock adiabat and Rayleigh line, namely as bounds on their relative slope
$M_{\boldsymbol{n}}=u_{\boldsymbol{n}}/c$
denotes the normal Mach number (Lax Reference Lax1957). The conditions for stability with respect to multidimensional perturbations can be conveniently related to geometric properties of the shock adiabat and Rayleigh line, namely as bounds on their relative slope
![]() $R$
,
$R$
,
with
![]() $P^{{\mathcal{H}}}(v;P_{A},v_{A})$
being the shock adiabat function implicitly defined by (2.3a
). D’yakov (Reference D’yakov1954) and Erpenbeck (Reference Erpenbeck1962) showed that the shock front is stable against ripple perturbations if and only if
$P^{{\mathcal{H}}}(v;P_{A},v_{A})$
being the shock adiabat function implicitly defined by (2.3a
). D’yakov (Reference D’yakov1954) and Erpenbeck (Reference Erpenbeck1962) showed that the shock front is stable against ripple perturbations if and only if
The stability range (2.8) was further restricted by Kontorovich (Reference Kontorovich1958) to read
by noting that in the interval
the shock front is only neutrally stable against transverse perturbations and can spontaneously emit acoustic waves (see also Fowles Reference Fowles1981). Erpenbeck (Reference Erpenbeck1963) and Gardner (Reference Gardner1963) also pointed out that violating the second inequality in (2.8) leads to non-uniqueness of solutions of the Riemann problem. Despite the fact that conditions (2.8) and (2.9) were derived from linear stability analysis of planar shocks, it turns out that an arbitrarily curved shock front is stable provided (2.9) is satisfied locally at each point of the front (Majda Reference Majda1983). Yet, for some cases, (2.5) and (2.9) may not be sufficient to rule out unphysical solutions of the Rankine–Hugoniot relations. Further and more selective criteria, such as requiring that the shock wave admit a one-dimensional thermoviscous profile, may solve the problem of defining the admissible shocks, although it must be noticed that there is no general theory for defining appropriate admissibility conditions that applies to arbitrary equations of state (Menikoff & Plohr Reference Menikoff and Plohr1989; Kluwick Reference Kluwick2001).
2.2 Properties of shock curves in classical gas dynamics
In the reference frame shown in figure 1, the Rankine–Hugoniot relations involve 8 parameters in total: the 2 velocity components (normal and tangent to the shock) and 2 thermodynamic quantities (e.g. pressure and density), for both the pre-shock and post-shock states. In these coordinates, the Rankine–Hugoniot relations consist of 4 functional relations (the equation of the tangential velocity (2.2b
) reduces to a scalar one), so that 4 remaining parameters are needed to parametrize the solution. The choice of this set of parameters is typically based on the specific context. On many occasions, for instance, one knows the evolution of the flow up to the point where a shock wave occurs. In this respect, it is customary to specify the thermodynamic state and the total or kinetic energy content of the flow upstream of the shock, which together correspond to a triplet such as, e.g.
![]() $\boldsymbol{A}=(P_{A},v_{A},\Vert \boldsymbol{u}_{A}\Vert )$
or
$\boldsymbol{A}=(P_{A},v_{A},\Vert \boldsymbol{u}_{A}\Vert )$
or
![]() $\boldsymbol{A}=(v_{A},s_{A},M_{A})$
. Any other equivalent triplet can be obtained by simple manipulation. Given a triplet
$\boldsymbol{A}=(v_{A},s_{A},M_{A})$
. Any other equivalent triplet can be obtained by simple manipulation. Given a triplet
![]() $\boldsymbol{A}$
, the Rankine–Hugoniot relations determine the state downstream of an oblique shock from the considered pre-shock state, as a function of
$\boldsymbol{A}$
, the Rankine–Hugoniot relations determine the state downstream of an oblique shock from the considered pre-shock state, as a function of
![]() $\unicode[STIX]{x1D6FD}$
, the angle between the shock front and the pre-shock flow direction (see figure 1). By analogy with one-dimensional unsteady flows (given a pre-shock state, one obtains the post-shock state as a function of the shock speed), the resulting locus is called the shock curve.
$\unicode[STIX]{x1D6FD}$
, the angle between the shock front and the pre-shock flow direction (see figure 1). By analogy with one-dimensional unsteady flows (given a pre-shock state, one obtains the post-shock state as a function of the shock speed), the resulting locus is called the shock curve.
In the following, some renowned properties of the shock curves of oblique shocks are recalled by resorting to analogies with the one-dimensional case. Our attention, hereinafter, will be restricted to single-phase fluids exhibiting
![]() $\unicode[STIX]{x1D6E4}>0$
in the vapour phase (BZT fluids are thus excluded), i.e. to classical gas dynamics in which shock waves are of the compressive type only. For a detailed discussion of shock curves for arbitrary equations of state, see Menikoff & Plohr (Reference Menikoff and Plohr1989) and Kluwick (Reference Kluwick2001). To establish notation, a quantity
$\unicode[STIX]{x1D6E4}>0$
in the vapour phase (BZT fluids are thus excluded), i.e. to classical gas dynamics in which shock waves are of the compressive type only. For a detailed discussion of shock curves for arbitrary equations of state, see Menikoff & Plohr (Reference Menikoff and Plohr1989) and Kluwick (Reference Kluwick2001). To establish notation, a quantity
![]() $X$
evaluated on the shock curve will be denoted as
$X$
evaluated on the shock curve will be denoted as
![]() $X^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})$
. On occasion, it will be useful to perform a change of independent variable; for ease of notation the same symbol
$X^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})$
. On occasion, it will be useful to perform a change of independent variable; for ease of notation the same symbol
![]() $X^{{\mathcal{H}}}$
will be maintained.
$X^{{\mathcal{H}}}$
will be maintained.
The properties of the shock curves can be conveniently analysed starting from their projection in a thermodynamic plane, namely the Hugoniot locus, solution set of equation (2.3a
) for a given pre-shock thermodynamic state
![]() $(P_{A},v_{A})$
. The Bethe–Weyl theorem (Bethe Reference Bethe1942; Weyl Reference Weyl1949) states that if
$(P_{A},v_{A})$
. The Bethe–Weyl theorem (Bethe Reference Bethe1942; Weyl Reference Weyl1949) states that if
![]() $\unicode[STIX]{x1D6E4}>0$
throughout the thermodynamic domain of interest, the Hugoniot locus is a continuous curve parametrized by the post-shock entropy and it satisfies
$\unicode[STIX]{x1D6E4}>0$
throughout the thermodynamic domain of interest, the Hugoniot locus is a continuous curve parametrized by the post-shock entropy and it satisfies
Substitution of
![]() $[v]<0$
into (2.3b
) immediately yields that compressive shock waves (
$[v]<0$
into (2.3b
) immediately yields that compressive shock waves (
![]() $[P]>0$
) only satisfy the entropy inequality and the first inequality in (2.6). By combining (2.3) with the fundamental thermodynamic identity
$[P]>0$
) only satisfy the entropy inequality and the first inequality in (2.6). By combining (2.3) with the fundamental thermodynamic identity
![]() $T\;\text{d}s=\text{d}h-v\;\text{d}P$
, one obtains
$T\;\text{d}s=\text{d}h-v\;\text{d}P$
, one obtains
thus showing that the Hugoniot locus can be parametrized also by the mass flux
![]() $m$
. Monotonicity of the mass flux implies that
$m$
. Monotonicity of the mass flux implies that
![]() $M_{\boldsymbol{n}A}>1$
along the compressive branch of the Hugoniot locus. Therefore, if
$M_{\boldsymbol{n}A}>1$
along the compressive branch of the Hugoniot locus. Therefore, if
![]() $\unicode[STIX]{x1D6E4}>0$
, compressive shock waves simultaneously fulfil the entropy inequality and the speed-ordering condition.
$\unicode[STIX]{x1D6E4}>0$
, compressive shock waves simultaneously fulfil the entropy inequality and the speed-ordering condition.
The Hugoniot locus can be also parametrized by the shock angle
![]() $\unicode[STIX]{x1D6FD}\in [\unicode[STIX]{x1D6FD}_{ac},\unicode[STIX]{x03C0}/2]$
, in which the lower bound
$\unicode[STIX]{x1D6FD}\in [\unicode[STIX]{x1D6FD}_{ac},\unicode[STIX]{x03C0}/2]$
, in which the lower bound
![]() $\unicode[STIX]{x1D6FD}_{ac}=\sin ^{-1}(1/M_{A})$
is the angle of the Mach lines or acoustic waves, corresponding a shock wave of vanishing intensity (
$\unicode[STIX]{x1D6FD}_{ac}=\sin ^{-1}(1/M_{A})$
is the angle of the Mach lines or acoustic waves, corresponding a shock wave of vanishing intensity (
![]() $[s]=0$
,
$[s]=0$
,
![]() $M_{\boldsymbol{n}}=1$
). Indeed,
$M_{\boldsymbol{n}}=1$
). Indeed,
![]() $u_{\boldsymbol{n}A}=\Vert \boldsymbol{u}_{A}\Vert \sin \unicode[STIX]{x1D6FD}$
, and hence differentiation of (2.4) yields the monotonicity condition
$u_{\boldsymbol{n}A}=\Vert \boldsymbol{u}_{A}\Vert \sin \unicode[STIX]{x1D6FD}$
, and hence differentiation of (2.4) yields the monotonicity condition
Any of the post-shock entropy, mass flux and shock angle (or another quantity that varies monotonically with one of these) can be regarded as measuring the shock strength. The
![]() $\unicode[STIX]{x1D6FD}$
-parametrization of the Hugoniot locus, in particular, appears as a natural choice in the context of oblique shock waves, where it allows for direct geometrical interpretation. Once the relationship between the pre-shock and post-shock thermodynamic quantities is determined as a function of the shock angle, the remaining kinematic quantities (post-shock velocity) are obtained from the conservation of mass (2.1a
) and tangential momentum (2.2b
); it follows that the shock angle parametrizes the shock curve.
$\unicode[STIX]{x1D6FD}$
-parametrization of the Hugoniot locus, in particular, appears as a natural choice in the context of oblique shock waves, where it allows for direct geometrical interpretation. Once the relationship between the pre-shock and post-shock thermodynamic quantities is determined as a function of the shock angle, the remaining kinematic quantities (post-shock velocity) are obtained from the conservation of mass (2.1a
) and tangential momentum (2.2b
); it follows that the shock angle parametrizes the shock curve.
We now comment on the dependence of selected thermodynamic and kinematic quantities of interest on the shock strength, which we conveniently identify with the shock angle
![]() $\unicode[STIX]{x1D6FD}$
. Firstly, the variation of the post-shock specific volume along the shock curve is considered, which ultimately determines the shape of the shock adiabat. By differentiating the Hugoniot relation (2.3a
), one finds that
$\unicode[STIX]{x1D6FD}$
. Firstly, the variation of the post-shock specific volume along the shock curve is considered, which ultimately determines the shape of the shock adiabat. By differentiating the Hugoniot relation (2.3a
), one finds that
where
![]() $G=v(\unicode[STIX]{x2202}P/\unicode[STIX]{x2202}e)_{v}$
is the Grüneisen coefficient, which has the same sign of the coefficient of thermal expansion. The post-shock specific volume decreases with increasing shock angle only if
$G=v(\unicode[STIX]{x2202}P/\unicode[STIX]{x2202}e)_{v}$
is the Grüneisen coefficient, which has the same sign of the coefficient of thermal expansion. The post-shock specific volume decreases with increasing shock angle only if
which is true in the limit of weak shocks, but may be violated for finite-strength shocks if
![]() $G$
is sufficiently large. Ordinary-shaped Hugoniot loci, however, do satisfy (2.15). This is the typical behaviour of the shock curves for most real fluids (see, e.g. Landau & Lifshitz Reference Landau and Lifshitz1987). Moreover, if
$G$
is sufficiently large. Ordinary-shaped Hugoniot loci, however, do satisfy (2.15). This is the typical behaviour of the shock curves for most real fluids (see, e.g. Landau & Lifshitz Reference Landau and Lifshitz1987). Moreover, if
![]() $G>0$
and thus the substance expands upon isobaric heating, which is true in most situations of interest (with the notable exception of water near freezing), equality in (2.15) determines the maximum density increase across compression shock waves. Combining the expressions of the variation of two independent thermodynamic quantities along the shock curve (e.g. the entropy and specific volume), the variation of any other post-shock thermodynamic quantities can be derived using the standard thermodynamic identities. It is readily obtained that if (2.15) holds (and
$G>0$
and thus the substance expands upon isobaric heating, which is true in most situations of interest (with the notable exception of water near freezing), equality in (2.15) determines the maximum density increase across compression shock waves. Combining the expressions of the variation of two independent thermodynamic quantities along the shock curve (e.g. the entropy and specific volume), the variation of any other post-shock thermodynamic quantities can be derived using the standard thermodynamic identities. It is readily obtained that if (2.15) holds (and
![]() $\unicode[STIX]{x1D6E4}>0$
by earlier assumption), the post-shock pressure, internal energy and enthalpy all increase with shock strength along the compression branch of the Hugoniot locus; the same holds for the temperature if
$\unicode[STIX]{x1D6E4}>0$
by earlier assumption), the post-shock pressure, internal energy and enthalpy all increase with shock strength along the compression branch of the Hugoniot locus; the same holds for the temperature if
![]() $G>0$
in addition. Monotonicity of
$G>0$
in addition. Monotonicity of
![]() $v^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})$
also guarantees that the shock adiabat is convex and that the shock front is stable with respect to multidimensional perturbations, cf. inequalities (2.8), though it might satisfy the conditions for spontaneous acoustic emission, namely the upper bound in (2.9) could be negative.
$v^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})$
also guarantees that the shock adiabat is convex and that the shock front is stable with respect to multidimensional perturbations, cf. inequalities (2.8), though it might satisfy the conditions for spontaneous acoustic emission, namely the upper bound in (2.9) could be negative.
A thermodynamic quantity of particular interest in this work is the speed of sound, since it is directly related to the occurrence of non-ideal effects across oblique shocks. The variation of the post-shock speed of sound along the shock curve is given by
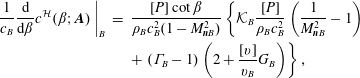 $$\begin{eqnarray}\displaystyle \frac{1}{c_{B}}\frac{\text{d}}{\text{d}\unicode[STIX]{x1D6FD}}c^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})\biggm\vert_{B} & = & \displaystyle \frac{[P]\cot \unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D70C}_{B}c_{B}^{2}(1-M_{\boldsymbol{n}B}^{2})}\left\{{\mathcal{K}}_{B}\frac{[P]}{\unicode[STIX]{x1D70C}_{B}c_{B}^{2}}\left(\frac{1}{M_{\boldsymbol{n}B}^{2}}-1\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\left.(\unicode[STIX]{x1D6E4}_{B}-1)\left(2+\frac{[v]}{v_{B}}G_{B}\right)\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{1}{c_{B}}\frac{\text{d}}{\text{d}\unicode[STIX]{x1D6FD}}c^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})\biggm\vert_{B} & = & \displaystyle \frac{[P]\cot \unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D70C}_{B}c_{B}^{2}(1-M_{\boldsymbol{n}B}^{2})}\left\{{\mathcal{K}}_{B}\frac{[P]}{\unicode[STIX]{x1D70C}_{B}c_{B}^{2}}\left(\frac{1}{M_{\boldsymbol{n}B}^{2}}-1\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\left.(\unicode[STIX]{x1D6E4}_{B}-1)\left(2+\frac{[v]}{v_{B}}G_{B}\right)\right\},\end{eqnarray}$$
where we introduced the dimensionless isochoric derivative of the speed of sound with the entropy
![]() ${\mathcal{K}}=(c/T)(\unicode[STIX]{x2202}c/\unicode[STIX]{x2202}s)_{v}$
. Assuming
${\mathcal{K}}=(c/T)(\unicode[STIX]{x2202}c/\unicode[STIX]{x2202}s)_{v}$
. Assuming
![]() ${\mathcal{K}}_{B}>0$
and that (2.15) is satisfied, the post-shock speed of sound increases with the shock strength along the compression branch of the shock curve if
${\mathcal{K}}_{B}>0$
and that (2.15) is satisfied, the post-shock speed of sound increases with the shock strength along the compression branch of the shock curve if
![]() $\unicode[STIX]{x1D6E4}_{B}>1$
, but can possibly decrease if
$\unicode[STIX]{x1D6E4}_{B}>1$
, but can possibly decrease if
![]() $\unicode[STIX]{x1D6E4}_{B}<1$
.
$\unicode[STIX]{x1D6E4}_{B}<1$
.
Finally, we report the variation of the post-shock Mach number along the shock curve, which allows us to evaluate the kinematic state of the flow in the post-shock state. By combining the variations of the velocity magnitude and speed of sound, one obtains
 $$\begin{eqnarray}\displaystyle \frac{1}{M_{B}}\frac{\text{d}}{\text{d}\unicode[STIX]{x1D6FD}}M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})\biggm\vert_{B} & = & \displaystyle \frac{[P]}{\unicode[STIX]{x1D70C}_{B}c_{B}^{2}}\frac{\cot \unicode[STIX]{x1D6FD}}{1-M_{\boldsymbol{n}B}^{2}}\left\{\frac{[v]}{v_{B}}(1-M_{\boldsymbol{n}B}^{2})\left({\mathcal{K}}_{B}+\frac{1+G_{B}}{M_{B}^{2}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\left.J_{B}\left(2+\frac{[v]}{v_{B}}G_{B}\right)\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{1}{M_{B}}\frac{\text{d}}{\text{d}\unicode[STIX]{x1D6FD}}M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})\biggm\vert_{B} & = & \displaystyle \frac{[P]}{\unicode[STIX]{x1D70C}_{B}c_{B}^{2}}\frac{\cot \unicode[STIX]{x1D6FD}}{1-M_{\boldsymbol{n}B}^{2}}\left\{\frac{[v]}{v_{B}}(1-M_{\boldsymbol{n}B}^{2})\left({\mathcal{K}}_{B}+\frac{1+G_{B}}{M_{B}^{2}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\left.J_{B}\left(2+\frac{[v]}{v_{B}}G_{B}\right)\right\},\end{eqnarray}$$
in which we have defined
which is a non-dimensional measure of the Mach number dependence on the density in isentropic flows with constant total enthalpy (see Thompson Reference Thompson1971; Cramer & Best Reference Cramer and Best1991). Assuming that
![]() ${\mathcal{K}}_{B}>0$
,
${\mathcal{K}}_{B}>0$
,
![]() $G_{B}>-1$
and (2.15) is satisfied, the post-shock Mach number decreases with increasing shock angle along the compression branch of the shock curve if
$G_{B}>-1$
and (2.15) is satisfied, the post-shock Mach number decreases with increasing shock angle along the compression branch of the shock curve if
![]() $J_{B}<0$
. If instead the values of the post-shock Mach number and fundamental derivative are such that
$J_{B}<0$
. If instead the values of the post-shock Mach number and fundamental derivative are such that
![]() $J_{B}>0$
, the post-shock Mach number can possibly increase.
$J_{B}>0$
, the post-shock Mach number can possibly increase.
2.3 Non-ideal oblique shocks
Within the context of classical gas dynamics, diverse qualitative differences can be found between shock waves in the ideal-gas and non-ideal regime. Anomalies that are related to violation of condition (2.15) and to fluid states exhibiting
![]() $G<0$
or
$G<0$
or
![]() ${\mathcal{K}}<0$
are discussed by Menikoff & Plohr (Reference Menikoff and Plohr1989). Here we restrict attention to compressibility-related effects that are caused by fluid states exhibiting
${\mathcal{K}}<0$
are discussed by Menikoff & Plohr (Reference Menikoff and Plohr1989). Here we restrict attention to compressibility-related effects that are caused by fluid states exhibiting
![]() $0<\unicode[STIX]{x1D6E4}<1$
, that are therefore not possible in the ideal-gas limit. The parameter
$0<\unicode[STIX]{x1D6E4}<1$
, that are therefore not possible in the ideal-gas limit. The parameter
![]() $\unicode[STIX]{x1D6E4}$
directly controls the sound speed variation in isentropic processes as well as adiabatic, possibly non-isentropic, processes (assuming
$\unicode[STIX]{x1D6E4}$
directly controls the sound speed variation in isentropic processes as well as adiabatic, possibly non-isentropic, processes (assuming
![]() ${\mathcal{K}}$
does not change its sign). For the case of oblique shock waves, the well-known formulas for ideal gases (see, e.g. Thompson Reference Thompson1988) indicate that the speed of sound necessarily increases across the shock (a consequence of the temperature rise). On the contrary, in the non-ideal gas dynamic regime, the speed of sound can possibly decrease following the adiabatic compression across an oblique shock, as suggested by relation (2.16).
${\mathcal{K}}$
does not change its sign). For the case of oblique shock waves, the well-known formulas for ideal gases (see, e.g. Thompson Reference Thompson1988) indicate that the speed of sound necessarily increases across the shock (a consequence of the temperature rise). On the contrary, in the non-ideal gas dynamic regime, the speed of sound can possibly decrease following the adiabatic compression across an oblique shock, as suggested by relation (2.16).
Because the flow velocity magnitude is required to decrease across a compressive shock (the normal component decreases by mass conservation while the tangential one is conserved by momentum balance), the peculiar behaviour of the speed of sound ultimately determines the variation of the Mach number across an oblique shock,
The speed-ordering condition (2.6) requires that the normal Mach number is larger in the pre-shock state than in the post-shock state. On the contrary, no constraint is imposed on the tangential Mach number
![]() $\Vert \boldsymbol{u}_{\boldsymbol{t}}\Vert /c$
, whose variation across the shock is inversely proportional to the sound speed. It follows that whenever
$\Vert \boldsymbol{u}_{\boldsymbol{t}}\Vert /c$
, whose variation across the shock is inversely proportional to the sound speed. It follows that whenever
![]() $c_{B}>c_{A}$
, as in the ideal-gas limit, the Mach number necessarily decreases across any admissible shock waves. If instead
$c_{B}>c_{A}$
, as in the ideal-gas limit, the Mach number necessarily decreases across any admissible shock waves. If instead
![]() $c_{B}<c_{A}$
, which is possible in the non-ideal regime, the Mach number can either decrease or increase across an oblique shock; the Mach number increase will occur if the sound speed decrease is sufficiently large that the increase in the tangential Mach number compensates the necessary decrease in the normal Mach number.
$c_{B}<c_{A}$
, which is possible in the non-ideal regime, the Mach number can either decrease or increase across an oblique shock; the Mach number increase will occur if the sound speed decrease is sufficiently large that the increase in the tangential Mach number compensates the necessary decrease in the normal Mach number.
Because the Mach number is the parameter of primary interest in many applications, the Mach number increase across oblique shock waves is arguably the most significant of all non-ideal compressible-fluid effects. In this sense, hereinafter we will refer to oblique shock waves featuring
![]() $M_{B}>M_{A}$
as non-ideal oblique shock waves. The analysis of the weak shock limit
$M_{B}>M_{A}$
as non-ideal oblique shock waves. The analysis of the weak shock limit
![]() $\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FD}_{ac}\ll 1$
provides a condition of existence of non-ideal oblique shocks in terms of pre-shock quantities, since Taylor series expansion of the post-shock Mach number in the neighbourhood of the acoustic angle reads
$\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FD}_{ac}\ll 1$
provides a condition of existence of non-ideal oblique shocks in terms of pre-shock quantities, since Taylor series expansion of the post-shock Mach number in the neighbourhood of the acoustic angle reads
For weak oblique shock waves, the sign of the Mach number variation is related to the values of the pre-shock fundamental derivative
![]() $\unicode[STIX]{x1D6E4}_{A}$
and Mach number
$\unicode[STIX]{x1D6E4}_{A}$
and Mach number
![]() $M_{A}$
only. If the combination of these values is such that
$M_{A}$
only. If the combination of these values is such that
![]() $J_{A}>0$
, the Mach number increases across a weak oblique shock. It is readily seen that if
$J_{A}>0$
, the Mach number increases across a weak oblique shock. It is readily seen that if
![]() $\unicode[STIX]{x1D6E4}_{A}<1$
non-ideal oblique shocks necessarily occur when
$\unicode[STIX]{x1D6E4}_{A}<1$
non-ideal oblique shocks necessarily occur when
![]() $M_{A}$
is sufficiently large. The role of the fundamental parameter
$M_{A}$
is sufficiently large. The role of the fundamental parameter
![]() $J$
will be further clarified in the following.
$J$
will be further clarified in the following.
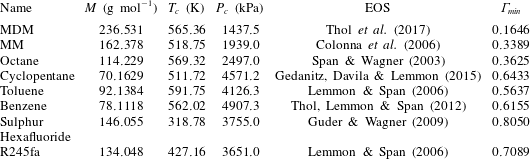
Table 1. Molecular weight
![]() $M$
, critical temperature
$M$
, critical temperature
![]() $T_{c}$
, critical pressure
$T_{c}$
, critical pressure
![]() $P_{c}$
for selected substances. The fluid properties are computed from the equation of state (EOS) indicated in the fifth column of the table;
$P_{c}$
for selected substances. The fluid properties are computed from the equation of state (EOS) indicated in the fifth column of the table;
![]() $\unicode[STIX]{x1D6E4}_{min}$
is the minimum value of the fundamental derivative in the vapour phase, as predicted by the EOS (
$\unicode[STIX]{x1D6E4}_{min}$
is the minimum value of the fundamental derivative in the vapour phase, as predicted by the EOS (
![]() $\unicode[STIX]{x1D6E4}_{min}$
occurs along the vapour–liquid equilibrium curve). Properties and thermodynamic models are taken from the well-established REFPROP library (Lemmon, Huber & McLinden Reference Lemmon, Huber and Mclinden2013).
$\unicode[STIX]{x1D6E4}_{min}$
occurs along the vapour–liquid equilibrium curve). Properties and thermodynamic models are taken from the well-established REFPROP library (Lemmon, Huber & McLinden Reference Lemmon, Huber and Mclinden2013).
3 The existence domain of non-ideal oblique shocks
This section addresses the flow conditions, in terms of pre-shock thermodynamic quantities and Mach number, resulting in the non-ideal Mach number increase across oblique shocks. The choice of pre-shock Mach number as the parameter accounting for the kinematic state of the fluid ahead of the shock waves is twofold. Firstly, it is the quantity that directly enters into the definition of the parameter
![]() $J$
, whose sign determines the direction of the Mach number variation across weak oblique shocks. Secondly, in the perfect-gas limit, several quantities of interest such as
$J$
, whose sign determines the direction of the Mach number variation across weak oblique shocks. Secondly, in the perfect-gas limit, several quantities of interest such as
![]() $\unicode[STIX]{x1D717}$
(deflection angle of the flow across the shock, see figure 1),
$\unicode[STIX]{x1D717}$
(deflection angle of the flow across the shock, see figure 1),
![]() $M_{B}$
,
$M_{B}$
,
![]() $P_{B}/P_{A}$
,
$P_{B}/P_{A}$
,
![]() $[s]$
, etc. (see, e.g. Thompson Reference Thompson1988), depend uniquely on
$[s]$
, etc. (see, e.g. Thompson Reference Thompson1988), depend uniquely on
![]() $M_{A}$
and
$M_{A}$
and
![]() $\unicode[STIX]{x1D6FD}$
. This also legitimizes the use of
$\unicode[STIX]{x1D6FD}$
. This also legitimizes the use of
![]() $\unicode[STIX]{x1D6FD}$
for the shock-curve parametrization in the perspective of evaluating the differences between ideal-gas and non-ideal regime.
$\unicode[STIX]{x1D6FD}$
for the shock-curve parametrization in the perspective of evaluating the differences between ideal-gas and non-ideal regime.
After identifying the different scenarios for the observation of non-ideal oblique shocks, the domain of pre-shock states that possibly lead to non-ideal oblique shocks is computed. The mentioned domain includes all the pre-shock states for which
![]() $M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})>M_{A}$
for some values of the shock angle. Results are given for each of the fluids listed in table 1.
$M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})>M_{A}$
for some values of the shock angle. Results are given for each of the fluids listed in table 1.
3.1 Influence of the pre-shock state
A parametric study is carried out to evaluate the dependence of
![]() $M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})$
on the pre-shock state, in the parameter space of pre-shock thermodynamic states and Mach number. To do this, we consider the projection of the shock curve on the
$M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})$
on the pre-shock state, in the parameter space of pre-shock thermodynamic states and Mach number. To do this, we consider the projection of the shock curve on the
![]() $M_{B}$
–
$M_{B}$
–
![]() $\unicode[STIX]{x1D6FD}$
plane for exemplary pre-shock states that allow to illustrate the different scenarios for the occurrence of non-ideal oblique shock waves.
$\unicode[STIX]{x1D6FD}$
plane for exemplary pre-shock states that allow to illustrate the different scenarios for the occurrence of non-ideal oblique shock waves.
The fluid employed here throughout for explanatory purposes is siloxane MDM (ocatmethyltrisiloxane, C
![]() $_{8}$
H
$_{8}$
H
![]() $_{24}$
O
$_{24}$
O
![]() $_{2}$
Si
$_{2}$
Si
![]() $_{3}$
), which is modelled via the state-of-the-art multiparameter equation of state reported in table 1 together with relevant thermophysical properties of MDM and of other substances considered in the following. MDM exhibits
$_{3}$
), which is modelled via the state-of-the-art multiparameter equation of state reported in table 1 together with relevant thermophysical properties of MDM and of other substances considered in the following. MDM exhibits
![]() $\unicode[STIX]{x1D6E4}_{min}<1$
, where
$\unicode[STIX]{x1D6E4}_{min}<1$
, where
![]() $\unicode[STIX]{x1D6E4}_{min}$
is the minimum value of the fundamental derivative in the vapour phase, indicating that the selected fluid is endowed with a finite vapour-phase
$\unicode[STIX]{x1D6E4}_{min}$
is the minimum value of the fundamental derivative in the vapour phase, indicating that the selected fluid is endowed with a finite vapour-phase
![]() $\unicode[STIX]{x1D6E4}<1$
region. Therefore, according to the arguments of the previous section, MDM is expected to allow for the occurrence of non-ideal oblique shock waves, provided the pre-shock state is carefully chosen. As for the other non-dimensional quantities that enter into the definition of the Mach number variation (2.17), MDM exhibits
$\unicode[STIX]{x1D6E4}<1$
region. Therefore, according to the arguments of the previous section, MDM is expected to allow for the occurrence of non-ideal oblique shock waves, provided the pre-shock state is carefully chosen. As for the other non-dimensional quantities that enter into the definition of the Mach number variation (2.17), MDM exhibits
![]() $G>0$
and
$G>0$
and
![]() ${\mathcal{K}}>0$
in the single phase vapour region to which this discussion is restricted. Moreover,
${\mathcal{K}}>0$
in the single phase vapour region to which this discussion is restricted. Moreover,
![]() $G$
is small enough that condition (2.15) is always satisfied along shock curves originating from pre-shock thermodynamic states in the vapour region.
$G$
is small enough that condition (2.15) is always satisfied along shock curves originating from pre-shock thermodynamic states in the vapour region.
In contrast to the case of perfect gases, for which the post-shock to pre-shock ratios of most quantities of interest can be expressed as functions of the pre-shock normal Mach number only, the full pre-shock state plays a major role in determining the properties of oblique shock waves for arbitrary equations of state. In order to facilitate the following analysis, two parametric studies are conducted. Firstly, a parametric analysis is carried out for a fixed pre-shock Mach number and for different pre-shock thermodynamic states. Secondly, the pre-shock thermodynamic state is fixed and the pre-shock Mach number is varied.
Figure 2 shows the variation of the post-shock Mach number with the shock angle for a fixed pre-shock Mach number
![]() $M_{A}=2$
and different pre-shock thermodynamic states selected along the same isentrope
$M_{A}=2$
and different pre-shock thermodynamic states selected along the same isentrope
![]() $s_{A}<s_{\unicode[STIX]{x1D70F}}$
, where
$s_{A}<s_{\unicode[STIX]{x1D70F}}$
, where
![]() $s_{\unicode[STIX]{x1D70F}}$
denotes the isentrope tangent to the locus
$s_{\unicode[STIX]{x1D70F}}$
denotes the isentrope tangent to the locus
![]() $J_{A}=0$
. Under the assumption that the pre-shock Mach number
$J_{A}=0$
. Under the assumption that the pre-shock Mach number
![]() $M_{A}$
is fixed, the locus
$M_{A}$
is fixed, the locus
![]() $J_{A}=0$
shown in figure 2 coincides with the
$J_{A}=0$
shown in figure 2 coincides with the
![]() $\unicode[STIX]{x1D6E4}$
-isoline
$\unicode[STIX]{x1D6E4}$
-isoline
![]() $\unicode[STIX]{x1D6E4}=1-1/M_{A}^{2}$
, see (2.18). The thermodynamic region between the
$\unicode[STIX]{x1D6E4}=1-1/M_{A}^{2}$
, see (2.18). The thermodynamic region between the
![]() $J_{A}=0$
locus and the saturated vapour curve embeds all the possible pre-shock states exhibiting
$J_{A}=0$
locus and the saturated vapour curve embeds all the possible pre-shock states exhibiting
![]() $J_{A}>0$
. Note that, according to (2.20), the function
$J_{A}>0$
. Note that, according to (2.20), the function
![]() $M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})$
corresponding to pre-shock thermodynamic states having
$M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})$
corresponding to pre-shock thermodynamic states having
![]() $J_{A}>0$
will exhibit positive initial slope, thus indicating that the flow Mach number increases across weak oblique shock waves. Four pre-shock thermodynamic states are now considered, as representative of the possible qualitative evolution of the post-shock Mach number along the shock curve. The triplets corresponding to the marked configurations are given by
$J_{A}>0$
will exhibit positive initial slope, thus indicating that the flow Mach number increases across weak oblique shock waves. Four pre-shock thermodynamic states are now considered, as representative of the possible qualitative evolution of the post-shock Mach number along the shock curve. The triplets corresponding to the marked configurations are given by
![]() $\boldsymbol{A}_{i}=(P(s_{A},v_{i}),v_{i},M_{A})$
,
$\boldsymbol{A}_{i}=(P(s_{A},v_{i}),v_{i},M_{A})$
,
![]() $i=1,\ldots ,4$
.
$i=1,\ldots ,4$
.

Figure 2. Shock curves for MDM in the post-shock Mach number–shock angle plane. The pre-shock Mach number is fixed to
![]() $M_{A}=2$
. The pre-shock thermodynamic states are selected along the same isentrope
$M_{A}=2$
. The pre-shock thermodynamic states are selected along the same isentrope
![]() $s_{A}=s(1.2743P_{c},v_{c})<s_{\unicode[STIX]{x1D70F}}$
, with
$s_{A}=s(1.2743P_{c},v_{c})<s_{\unicode[STIX]{x1D70F}}$
, with
![]() $s_{\unicode[STIX]{x1D70F}}$
denoting the isentrope tangent to the locus
$s_{\unicode[STIX]{x1D70F}}$
denoting the isentrope tangent to the locus
![]() $J_{A}=0$
(corresponding to the
$J_{A}=0$
(corresponding to the
![]() $\unicode[STIX]{x1D6E4}$
-isoline
$\unicode[STIX]{x1D6E4}$
-isoline
![]() $\unicode[STIX]{x1D6E4}=1-1/M_{A}^{2}$
). Marked configurations:
$\unicode[STIX]{x1D6E4}=1-1/M_{A}^{2}$
). Marked configurations:
![]() $v_{1}=v_{c}$
,
$v_{1}=v_{c}$
,
![]() $v_{2}=5v_{c}$
,
$v_{2}=5v_{c}$
,
![]() $v_{3}=8v_{c}$
,
$v_{3}=8v_{c}$
,
![]() $v_{3}=11v_{c}$
. The red portions of the shock curves correspond to neutral stability of the shock front against transverse perturbations (acoustic emission). Also shown is the ideal-gas limit (dash-dotted curve) and the locus of the stationary points of
$v_{3}=11v_{c}$
. The red portions of the shock curves correspond to neutral stability of the shock front against transverse perturbations (acoustic emission). Also shown is the ideal-gas limit (dash-dotted curve) and the locus of the stationary points of
![]() $M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})$
for pre-shock thermodynamic states along the isentrope considered (dashed curve). VLE: liquid-vapour equilibrium (saturation) curve.
$M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})$
for pre-shock thermodynamic states along the isentrope considered (dashed curve). VLE: liquid-vapour equilibrium (saturation) curve.
State
![]() $\boldsymbol{A}_{1}$
is considered first, which is located on the left-hand side (higher densities) of the region
$\boldsymbol{A}_{1}$
is considered first, which is located on the left-hand side (higher densities) of the region
![]() $J_{A}>0$
. As shown in figure 2, along the shock curve originating from state
$J_{A}>0$
. As shown in figure 2, along the shock curve originating from state
![]() $\boldsymbol{A}_{1}$
, the post-shock Mach number monotonically decreases with increasing shock angle. Exemplary non-monotonic Mach number variations are those corresponding to pre-shock states
$\boldsymbol{A}_{1}$
, the post-shock Mach number monotonically decreases with increasing shock angle. Exemplary non-monotonic Mach number variations are those corresponding to pre-shock states
![]() $\boldsymbol{A}_{2}$
and
$\boldsymbol{A}_{2}$
and
![]() $\boldsymbol{A}_{3}$
in figure 2. State
$\boldsymbol{A}_{3}$
in figure 2. State
![]() $\boldsymbol{A}_{2}$
is taken as representative of the Mach number evolution for pre-shock states featuring
$\boldsymbol{A}_{2}$
is taken as representative of the Mach number evolution for pre-shock states featuring
![]() $J_{A}>0$
. Thus, for increasing shock angles starting from
$J_{A}>0$
. Thus, for increasing shock angles starting from
![]() $\unicode[STIX]{x1D6FD}_{ac}$
, the post-shock Mach number initially increases. As the magnitude of the tangential velocity decreases (i.e. with increasing shock angle),
$\unicode[STIX]{x1D6FD}_{ac}$
, the post-shock Mach number initially increases. As the magnitude of the tangential velocity decreases (i.e. with increasing shock angle),
![]() $M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A}_{2})$
reaches a local maximum and subsequently decreases towards the subsonic values characterizing strong oblique shocks. For shock curves qualitatively similar to the present case
$M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A}_{2})$
reaches a local maximum and subsequently decreases towards the subsonic values characterizing strong oblique shocks. For shock curves qualitatively similar to the present case
![]() $\boldsymbol{A}_{2}$
, there exists a shock angle value
$\boldsymbol{A}_{2}$
, there exists a shock angle value
![]() $\tilde{\unicode[STIX]{x1D6FD}}=\tilde{\unicode[STIX]{x1D6FD}}(\boldsymbol{A})$
,
$\tilde{\unicode[STIX]{x1D6FD}}=\tilde{\unicode[STIX]{x1D6FD}}(\boldsymbol{A})$
,
![]() $\tilde{\unicode[STIX]{x1D6FD}}\neq \unicode[STIX]{x1D6FD}_{ac}$
, such that
$\tilde{\unicode[STIX]{x1D6FD}}\neq \unicode[STIX]{x1D6FD}_{ac}$
, such that
![]() $M^{{\mathcal{H}}}(\tilde{\unicode[STIX]{x1D6FD}};\boldsymbol{A})=M_{A}$
. Note, however, that the computed shock curve exhibits a fairly large interval of shock angles for which the conditions of spontaneous acoustic emission are satisfied, and thus the shock front is neutrally stable.
$M^{{\mathcal{H}}}(\tilde{\unicode[STIX]{x1D6FD}};\boldsymbol{A})=M_{A}$
. Note, however, that the computed shock curve exhibits a fairly large interval of shock angles for which the conditions of spontaneous acoustic emission are satisfied, and thus the shock front is neutrally stable.
If the pre-shock state exhibits
![]() $J_{A}<0$
, yet the thermodynamic state is selected in close proximity to the region
$J_{A}<0$
, yet the thermodynamic state is selected in close proximity to the region
![]() $J_{A}>0$
, as for case
$J_{A}>0$
, as for case
![]() $\boldsymbol{A}_{3}$
in figure 2, the post-shock Mach number features an interesting non-monotonic profile comprising two stationary points, with the local minimum (maximum) occurring at
$\boldsymbol{A}_{3}$
in figure 2, the post-shock Mach number features an interesting non-monotonic profile comprising two stationary points, with the local minimum (maximum) occurring at
![]() $M_{B}<M_{A}$
(
$M_{B}<M_{A}$
(
![]() $M_{B}>M_{A}$
). Configurations qualitatively similar to
$M_{B}>M_{A}$
). Configurations qualitatively similar to
![]() $\boldsymbol{A}_{3}$
thus exhibit two different shock angles
$\boldsymbol{A}_{3}$
thus exhibit two different shock angles
![]() $\tilde{\unicode[STIX]{x1D6FD}}_{1}=\tilde{\unicode[STIX]{x1D6FD}}_{1}(\boldsymbol{A})$
and
$\tilde{\unicode[STIX]{x1D6FD}}_{1}=\tilde{\unicode[STIX]{x1D6FD}}_{1}(\boldsymbol{A})$
and
![]() $\tilde{\unicode[STIX]{x1D6FD}}_{2}=\tilde{\unicode[STIX]{x1D6FD}}_{2}(\boldsymbol{A})$
, other than the acoustic angle, such that
$\tilde{\unicode[STIX]{x1D6FD}}_{2}=\tilde{\unicode[STIX]{x1D6FD}}_{2}(\boldsymbol{A})$
, other than the acoustic angle, such that
![]() $M^{{\mathcal{H}}}(\tilde{\unicode[STIX]{x1D6FD}}_{1};\boldsymbol{A})=M^{{\mathcal{H}}}(\tilde{\unicode[STIX]{x1D6FD}}_{2};\boldsymbol{A})=M_{A}$
; these angles delimit the
$M^{{\mathcal{H}}}(\tilde{\unicode[STIX]{x1D6FD}}_{1};\boldsymbol{A})=M^{{\mathcal{H}}}(\tilde{\unicode[STIX]{x1D6FD}}_{2};\boldsymbol{A})=M_{A}$
; these angles delimit the
![]() $\unicode[STIX]{x1D6FD}$
interval of Mach number increasing oblique shocks. It must be noticed, however, that a significantly larger portion of the shock curve of case
$\unicode[STIX]{x1D6FD}$
interval of Mach number increasing oblique shocks. It must be noticed, however, that a significantly larger portion of the shock curve of case
![]() $\boldsymbol{A}_{3}$
(in particular, of the portion corresponding to non-ideal oblique shocks) is predicted to satisfy the conditions for acoustic emission.
$\boldsymbol{A}_{3}$
(in particular, of the portion corresponding to non-ideal oblique shocks) is predicted to satisfy the conditions for acoustic emission.
By increasing the pre-shock specific volume along the reference isentrope, the two stationary points found in
![]() $\boldsymbol{A}_{3}$
-like configurations occur at
$\boldsymbol{A}_{3}$
-like configurations occur at
![]() $M_{B}<M_{A}$
and ultimately become coincident. Therefore, any further increase in
$M_{B}<M_{A}$
and ultimately become coincident. Therefore, any further increase in
![]() $v_{A}$
is such that the post-shock Mach number monotonically decreases with increasing shock angle. Note, however, that
$v_{A}$
is such that the post-shock Mach number monotonically decreases with increasing shock angle. Note, however, that
![]() $M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})$
profiles originating from pre-shock thermodynamic states relatively close to the region
$M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})$
profiles originating from pre-shock thermodynamic states relatively close to the region
![]() $J_{A}>0$
can still exhibit a somewhat anomalous, non-ideal curvature (due to the sound speed decrease) as shown in the exemplary case
$J_{A}>0$
can still exhibit a somewhat anomalous, non-ideal curvature (due to the sound speed decrease) as shown in the exemplary case
![]() $\boldsymbol{A}_{4}$
of figure 2.
$\boldsymbol{A}_{4}$
of figure 2.
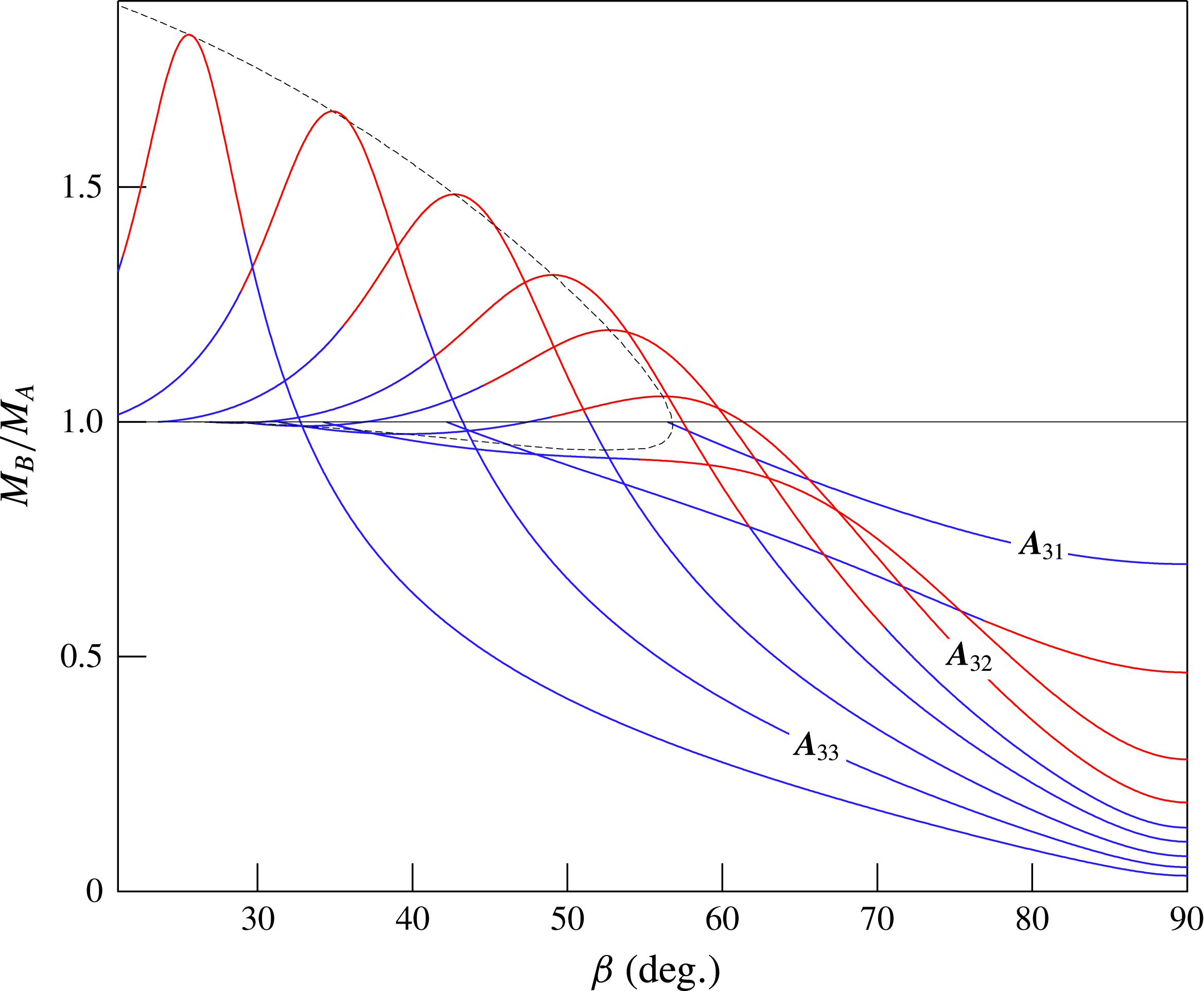
Figure 3. Shock curves for MDM in the post-shock Mach number–shock angle plane. The pre-shock thermodynamic state is fixed and corresponds to case 3 of figure 2, namely
![]() $s_{A}=s(1.2743P_{c},v_{c})$
,
$s_{A}=s(1.2743P_{c},v_{c})$
,
![]() $v_{A}=8v_{c}$
. Each curve corresponds to a different pre-shock Mach number. Marked configurations:
$v_{A}=8v_{c}$
. Each curve corresponds to a different pre-shock Mach number. Marked configurations:
![]() $M_{31}=1.2$
,
$M_{31}=1.2$
,
![]() $M_{32}=1.9$
,
$M_{32}=1.9$
,
![]() $M_{33}=3$
. The red portions of the shock curves correspond to neutral stability of the shock front against transverse perturbations (acoustic emission). Also shown is the locus of the stationary points of
$M_{33}=3$
. The red portions of the shock curves correspond to neutral stability of the shock front against transverse perturbations (acoustic emission). Also shown is the locus of the stationary points of
![]() $M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})$
for pre-shock thermodynamic states along the isentrope considered (dashed curve).
$M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})$
for pre-shock thermodynamic states along the isentrope considered (dashed curve).
Next, a complementary parametric study is presented, which is carried out by fixing the pre-shock thermodynamic state and considering different pre-shock Mach numbers. Figure 3 shows exemplary variations of the post-shock Mach number with the shock angle obtained from the same pre-shock thermodynamic state, which corresponds to case 3 of figure 2, and different values of the pre-shock Mach number. The triplets corresponding to the marked configurations are given by
![]() $\boldsymbol{A}_{i}=(P(s_{A},v_{3}),v_{3},M_{3i})$
,
$\boldsymbol{A}_{i}=(P(s_{A},v_{3}),v_{3},M_{3i})$
,
![]() $i=1,\ldots ,3$
. As in the previous study, selected configurations are detailed, as representative of the shock curve dependence on the pre-shock Mach number. For sufficiently low values of the pre-shock Mach number,
$i=1,\ldots ,3$
. As in the previous study, selected configurations are detailed, as representative of the shock curve dependence on the pre-shock Mach number. For sufficiently low values of the pre-shock Mach number,
![]() $M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})$
is monotonically decreasing (case
$M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})$
is monotonically decreasing (case
![]() $\boldsymbol{A}_{31}$
). By increasing the pre-shock Mach number,
$\boldsymbol{A}_{31}$
). By increasing the pre-shock Mach number,
![]() $M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})$
eventually develops an inflection point; any further increase leads to a non-monotonic configuration. As in the previous parametric study, two different configurations can possibly occur. For pre-shock Mach numbers slightly larger than the limiting value for the formation of an inflection point, the profile of post-shock Mach number is qualitatively similar to that of case
$M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})$
eventually develops an inflection point; any further increase leads to a non-monotonic configuration. As in the previous parametric study, two different configurations can possibly occur. For pre-shock Mach numbers slightly larger than the limiting value for the formation of an inflection point, the profile of post-shock Mach number is qualitatively similar to that of case
![]() $\boldsymbol{A}_{32}$
, which exhibits both a local minimum and a local maximum. If the pre-shock Mach number is sufficiently large, instead, the initial slope of
$\boldsymbol{A}_{32}$
, which exhibits both a local minimum and a local maximum. If the pre-shock Mach number is sufficiently large, instead, the initial slope of
![]() $M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})$
is necessarily positive (cf. (2.18) and (2.20), with
$M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})$
is necessarily positive (cf. (2.18) and (2.20), with
![]() $\unicode[STIX]{x1D6E4}_{A}<1$
), and the shock curve becomes qualitatively similar to case
$\unicode[STIX]{x1D6E4}_{A}<1$
), and the shock curve becomes qualitatively similar to case
![]() $\boldsymbol{A}_{33}$
. Again, acoustic emission is predicted to occur over large portions of the shock curves.
$\boldsymbol{A}_{33}$
. Again, acoustic emission is predicted to occur over large portions of the shock curves.
3.2 Computing the existence domain
Based upon the results of the previous section, the flow conditions resulting in the non-ideal Mach number increases across oblique shocks are collectively considered to single out each possible pre-shock state, in terms of pre-shock thermodynamic quantities and Mach number, for which
![]() $M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})>M_{A}$
for some values of the shock angle. The result is the definition of the domain of existence of non-ideal oblique shocks in the parameter space of pre-shock thermodynamic states and Mach number. For pre-shock states in this domain, there exists at least one value of the shock angle leading to
$M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})>M_{A}$
for some values of the shock angle. The result is the definition of the domain of existence of non-ideal oblique shocks in the parameter space of pre-shock thermodynamic states and Mach number. For pre-shock states in this domain, there exists at least one value of the shock angle leading to
![]() $M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})>M_{A}$
.
$M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})>M_{A}$
.
A convenient procedure for the computation of the existence domain of non-ideal oblique shocks is presented here. In order to reduce the complexity associated with the dependence of the shock properties on each of the pre-shock variables, we consider a fixed pre-shock Mach number, thus isolating the contribution of the pre-shock thermodynamic state. For a given pre-shock Mach number
![]() $M_{A}$
, the proposed method consists in determining, for each value of the pre-shock entropy, the limit values of the pre-shock pressure or density that bound the range where the shock curve possibly exhibits
$M_{A}$
, the proposed method consists in determining, for each value of the pre-shock entropy, the limit values of the pre-shock pressure or density that bound the range where the shock curve possibly exhibits
![]() $M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})>M_{A}$
for some values of the shock angle. These limit thermodynamic states define a locus delimiting the region in which the pre-shock thermodynamic state must be selected (together with the given
$M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})>M_{A}$
for some values of the shock angle. These limit thermodynamic states define a locus delimiting the region in which the pre-shock thermodynamic state must be selected (together with the given
![]() $M_{A}$
) in order to observe a non-ideal oblique shock. As the pre-shock Mach number is varied, this procedure determines a one-parameter family of thermodynamic regions embedding all the pre-shock states from which non-ideal oblique shock can possibly occur.
$M_{A}$
) in order to observe a non-ideal oblique shock. As the pre-shock Mach number is varied, this procedure determines a one-parameter family of thermodynamic regions embedding all the pre-shock states from which non-ideal oblique shock can possibly occur.
The proposed approach is first illustrated for MDM and one value of
![]() $M_{A}$
and then it is applied in the next section to the fluids listed in table 1 for several values of
$M_{A}$
and then it is applied in the next section to the fluids listed in table 1 for several values of
![]() $M_{A}$
, confirming the general validity and applicability of the concept outlined here.
$M_{A}$
, confirming the general validity and applicability of the concept outlined here.
In § 2.3, the shock curves considered were entirely enclosed in the single-phase vapour region. Here we consider also the cases in which the shock curves enter the two-phase region, limiting the discussion to their single-phase vapour portion. The shock angle leading to post-shock saturated conditions will be denoted by
![]() $\unicode[STIX]{x1D6FD}_{sat}=\unicode[STIX]{x1D6FD}_{sat}(\boldsymbol{A})$
. Crossing the liquid–vapour equilibrium curve (VLE or saturation curve) possibly occurs if a portion of the saturated vapour boundary is retrograde, which means that certain isentropes (and in turn, some shock adiabats) cross the phase boundary from the single towards the two-phase region, in the direction of increasing density. Siloxane fluid MDM is one such case of fluid with retrograde behaviour. Note, in this respect, that substances featuring
$\unicode[STIX]{x1D6FD}_{sat}=\unicode[STIX]{x1D6FD}_{sat}(\boldsymbol{A})$
. Crossing the liquid–vapour equilibrium curve (VLE or saturation curve) possibly occurs if a portion of the saturated vapour boundary is retrograde, which means that certain isentropes (and in turn, some shock adiabats) cross the phase boundary from the single towards the two-phase region, in the direction of increasing density. Siloxane fluid MDM is one such case of fluid with retrograde behaviour. Note, in this respect, that substances featuring
![]() $\unicode[STIX]{x1D6E4}<1$
regions in the vapour phase typically have heat capacities large enough that a portion of the saturated vapour boundary is retrograde (see Thompson, Carofano & Kim Reference Thompson, Carofano and Kim1986).
$\unicode[STIX]{x1D6E4}<1$
regions in the vapour phase typically have heat capacities large enough that a portion of the saturated vapour boundary is retrograde (see Thompson, Carofano & Kim Reference Thompson, Carofano and Kim1986).
With reference to the parametric studies carried out in § 3.1, three different types of
![]() $M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})$
profiles were identified. These include the ideal-gas-like (Mach number decreasing) case and two non-ideal cases (possibly Mach number increasing); the latter were distinguished depending on the positive/negative slope in the weak shock limit. For the ideal configuration, it can be noticed that, if the shock adiabat is entirely enclosed within the thermodynamic region
$M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})$
profiles were identified. These include the ideal-gas-like (Mach number decreasing) case and two non-ideal cases (possibly Mach number increasing); the latter were distinguished depending on the positive/negative slope in the weak shock limit. For the ideal configuration, it can be noticed that, if the shock adiabat is entirely enclosed within the thermodynamic region
![]() $\unicode[STIX]{x1D6E4}>1-1/M_{A}^{2}$
, the function
$\unicode[STIX]{x1D6E4}>1-1/M_{A}^{2}$
, the function
![]() $M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})$
is monotonically decreasing. This follows from the fact that
$M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})$
is monotonically decreasing. This follows from the fact that
![]() $M_{B}<M_{A}$
for weak shocks, with
$M_{B}<M_{A}$
for weak shocks, with
![]() $J_{A}<0$
, and from
$J_{A}<0$
, and from
![]() $\unicode[STIX]{x1D6E4}_{B}>1-M_{A}^{2}$
, which therefore gives
$\unicode[STIX]{x1D6E4}_{B}>1-M_{A}^{2}$
, which therefore gives
![]() $J_{B}<0$
along the shock curve. Substituting this into relation (2.17) yields the monotonicity of the post-shock Mach number with the shock angle (
$J_{B}<0$
along the shock curve. Substituting this into relation (2.17) yields the monotonicity of the post-shock Mach number with the shock angle (
![]() ${\mathcal{K}}>0$
,
${\mathcal{K}}>0$
,
![]() $G>0$
and (2.15) holds from earlier assumption). Examples of shock adiabats that satisfy the aforementioned condition are those originating from pre-shock states exhibiting
$G>0$
and (2.15) holds from earlier assumption). Examples of shock adiabats that satisfy the aforementioned condition are those originating from pre-shock states exhibiting
![]() $s_{A}>s_{\unicode[STIX]{x1D70F}}$
or from pre-shock states
$s_{A}>s_{\unicode[STIX]{x1D70F}}$
or from pre-shock states
![]() $s_{A}<s_{\unicode[STIX]{x1D70F}}$
that are either on the left-hand side of the
$s_{A}<s_{\unicode[STIX]{x1D70F}}$
that are either on the left-hand side of the
![]() $J_{A}>0$
region (case
$J_{A}>0$
region (case
![]() $\boldsymbol{A}_{1}$
in figure 2) or entering the two-phase region at a point where
$\boldsymbol{A}_{1}$
in figure 2) or entering the two-phase region at a point where
![]() $\unicode[STIX]{x1D6E4}>1-/M_{A}^{2}$
.
$\unicode[STIX]{x1D6E4}>1-/M_{A}^{2}$
.
On the other hand, shock curve originating from pre-shock states featuring
![]() $J_{A}>0$
necessarily lead to
$J_{A}>0$
necessarily lead to
![]() $M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})$
profiles embedding a non-ideal portion
$M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})$
profiles embedding a non-ideal portion
![]() $M_{B}\geqslant M_{A}$
. This range is of the type
$M_{B}\geqslant M_{A}$
. This range is of the type
![]() $\unicode[STIX]{x1D6FD}\in [\unicode[STIX]{x1D6FD}_{ac},\tilde{\unicode[STIX]{x1D6FD}}]$
, see case
$\unicode[STIX]{x1D6FD}\in [\unicode[STIX]{x1D6FD}_{ac},\tilde{\unicode[STIX]{x1D6FD}}]$
, see case
![]() $\boldsymbol{A}_{2}$
in figure 2, or of the type
$\boldsymbol{A}_{2}$
in figure 2, or of the type
![]() $\unicode[STIX]{x1D6FD}\in [\unicode[STIX]{x1D6FD}_{ac},\unicode[STIX]{x1D6FD}_{sat}]$
if the shock curve enters the two-phase region within the Mach number increasing portion, that is
$\unicode[STIX]{x1D6FD}\in [\unicode[STIX]{x1D6FD}_{ac},\unicode[STIX]{x1D6FD}_{sat}]$
if the shock curve enters the two-phase region within the Mach number increasing portion, that is
![]() $M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD}_{sat};\boldsymbol{A})>M_{A}$
.
$M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD}_{sat};\boldsymbol{A})>M_{A}$
.
Finally, it was shown that pre-shock states satisfying
![]() $s_{A}<s_{\unicode[STIX]{x1D70F}}$
and
$s_{A}<s_{\unicode[STIX]{x1D70F}}$
and
![]() $J_{A}<0$
, yet in the close proximity of the low-density zero of
$J_{A}<0$
, yet in the close proximity of the low-density zero of
![]() $J_{A}$
along the selected isentrope, possibly lead to
$J_{A}$
along the selected isentrope, possibly lead to
![]() $M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})$
functions of the non-ideal type. In this case, the interval of shock angles corresponding to
$M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})$
functions of the non-ideal type. In this case, the interval of shock angles corresponding to
![]() $M_{B}\geqslant M_{A}$
is of the form
$M_{B}\geqslant M_{A}$
is of the form
![]() $\unicode[STIX]{x1D6FD}\in [\tilde{\unicode[STIX]{x1D6FD}}_{1},\tilde{\unicode[STIX]{x1D6FD}}_{2}]$
, see case
$\unicode[STIX]{x1D6FD}\in [\tilde{\unicode[STIX]{x1D6FD}}_{1},\tilde{\unicode[STIX]{x1D6FD}}_{2}]$
, see case
![]() $\boldsymbol{A}_{3}$
in figure 2, or of the form
$\boldsymbol{A}_{3}$
in figure 2, or of the form
![]() $\unicode[STIX]{x1D6FD}\in [\tilde{\unicode[STIX]{x1D6FD}}_{1},\unicode[STIX]{x1D6FD}_{sat}]$
if
$\unicode[STIX]{x1D6FD}\in [\tilde{\unicode[STIX]{x1D6FD}}_{1},\unicode[STIX]{x1D6FD}_{sat}]$
if
![]() $M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD}_{sat};\boldsymbol{A})>M_{A}$
.
$M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD}_{sat};\boldsymbol{A})>M_{A}$
.
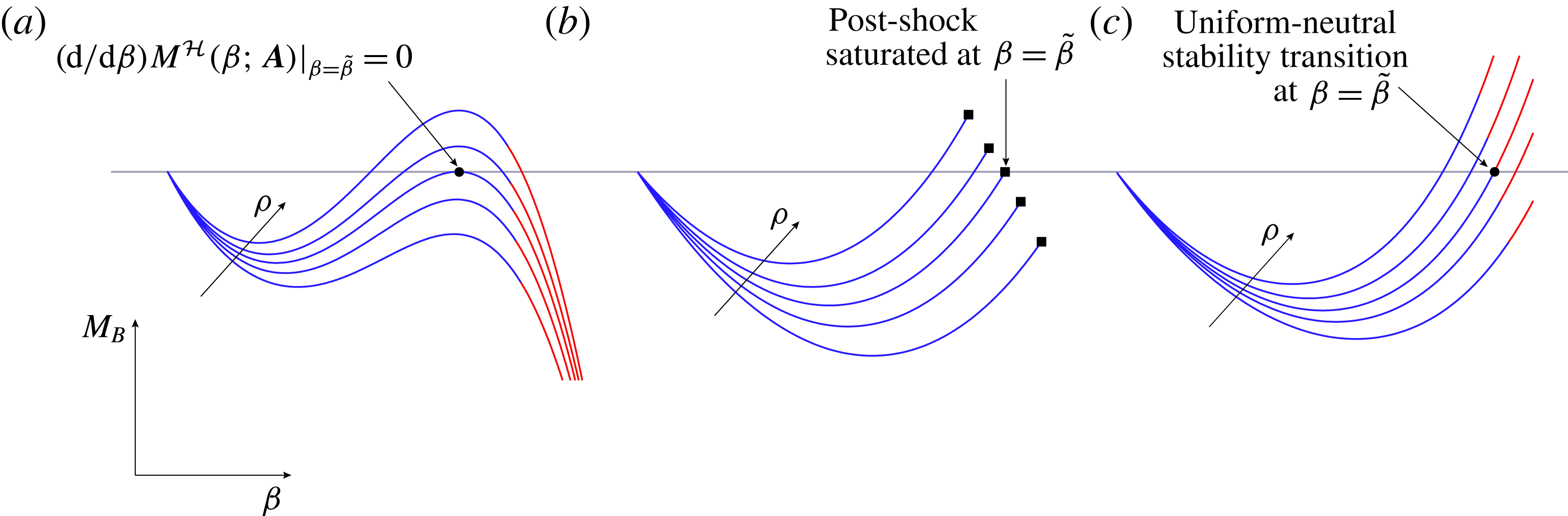
Figure 4. Illustration of the limit shock curves in the
![]() $M_{B}$
–
$M_{B}$
–
![]() $\unicode[STIX]{x1D6FD}$
diagram. Solid squares: post-shock saturated conditions; red line: acoustic emission is predicted to occur. The shock angle
$\unicode[STIX]{x1D6FD}$
diagram. Solid squares: post-shock saturated conditions; red line: acoustic emission is predicted to occur. The shock angle
![]() $\tilde{\unicode[STIX]{x1D6FD}}\neq \unicode[STIX]{x1D6FD}_{ac}$
indicates that the Mach number is preserved across the shock, namely
$\tilde{\unicode[STIX]{x1D6FD}}\neq \unicode[STIX]{x1D6FD}_{ac}$
indicates that the Mach number is preserved across the shock, namely
![]() $M^{{\mathcal{H}}}(\tilde{\unicode[STIX]{x1D6FD}};\boldsymbol{A})=M_{A}$
. (a) The limit curve exhibits
$M^{{\mathcal{H}}}(\tilde{\unicode[STIX]{x1D6FD}};\boldsymbol{A})=M_{A}$
. (a) The limit curve exhibits
![]() $\text{d}M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})/\text{d}\unicode[STIX]{x1D6FD}|_{\unicode[STIX]{x1D6FD}=\tilde{\unicode[STIX]{x1D6FD}}}=0$
; (b) on the limit curve, the post-shock thermodynamic state associated with
$\text{d}M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})/\text{d}\unicode[STIX]{x1D6FD}|_{\unicode[STIX]{x1D6FD}=\tilde{\unicode[STIX]{x1D6FD}}}=0$
; (b) on the limit curve, the post-shock thermodynamic state associated with
![]() $\unicode[STIX]{x1D6FD}=\tilde{\unicode[STIX]{x1D6FD}}$
lies on saturated phase boundary; (c) transition from uniform to neutral stability occurs at
$\unicode[STIX]{x1D6FD}=\tilde{\unicode[STIX]{x1D6FD}}$
lies on saturated phase boundary; (c) transition from uniform to neutral stability occurs at
![]() $\unicode[STIX]{x1D6FD}=\tilde{\unicode[STIX]{x1D6FD}}$
on the limit curve.
$\unicode[STIX]{x1D6FD}=\tilde{\unicode[STIX]{x1D6FD}}$
on the limit curve.
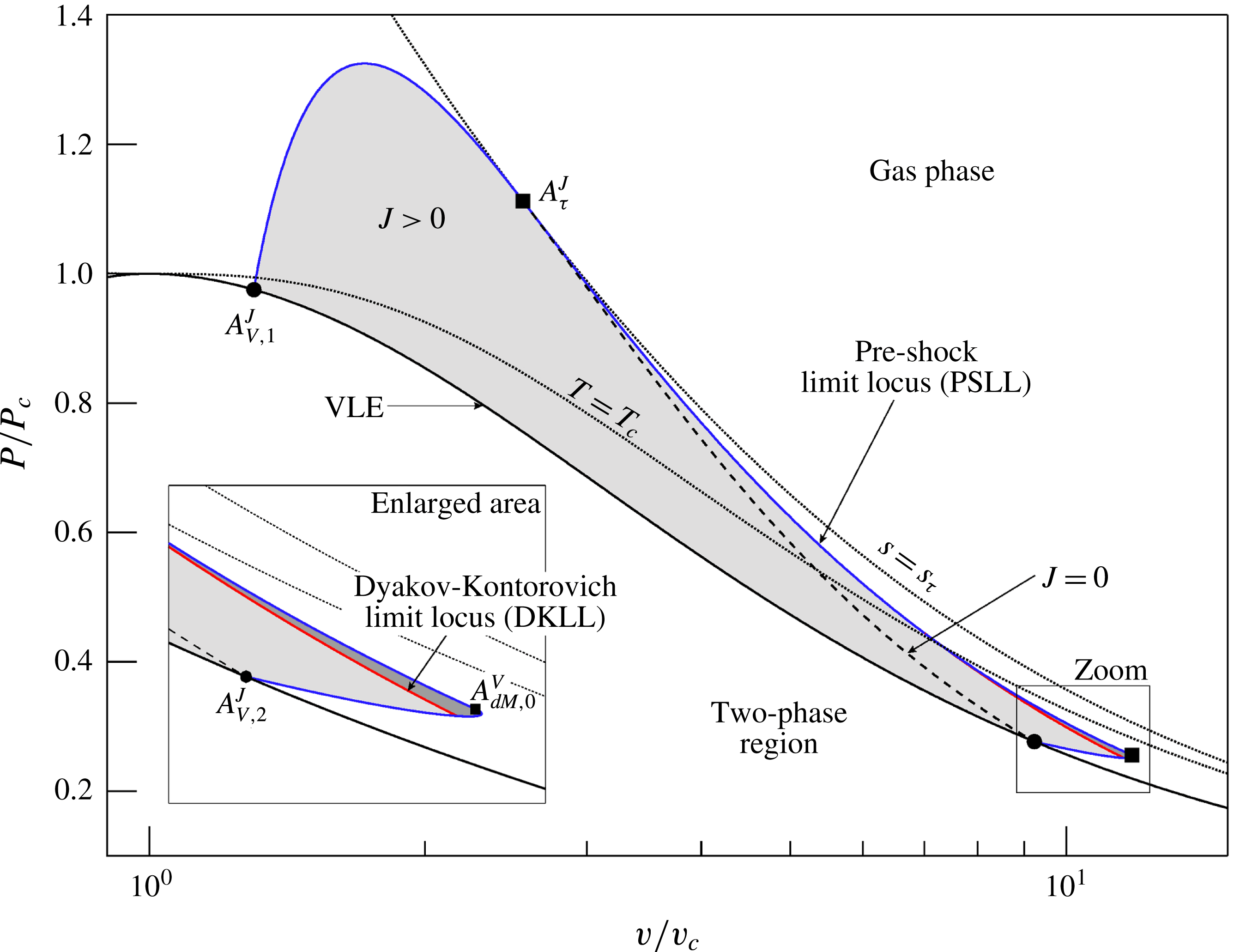
Figure 5. Pre-shock state domain (shaded area) for non-ideal oblique shock waves in MDM with fixed pre-shock Mach number
![]() $M_{A}=2$
. The domain is bounded by the pre-shock limit locus (PSLL, blue line) and by the vapour–liquid equilibrium (VLE) line. Points
$M_{A}=2$
. The domain is bounded by the pre-shock limit locus (PSLL, blue line) and by the vapour–liquid equilibrium (VLE) line. Points
![]() $A_{V,1}^{J}$
and
$A_{V,1}^{J}$
and
![]() $A_{V,2}^{J}$
indicate the high- and low-density intersection, respectively, of the
$A_{V,2}^{J}$
indicate the high- and low-density intersection, respectively, of the
![]() $J_{A}=0$
locus with the VLE line. The isentrope passing through
$J_{A}=0$
locus with the VLE line. The isentrope passing through
![]() $A_{\unicode[STIX]{x1D70F}}^{J}$
is tangent to the
$A_{\unicode[STIX]{x1D70F}}^{J}$
is tangent to the
![]() $J_{A}=0$
locus. The shock curve centred on
$J_{A}=0$
locus. The shock curve centred on
![]() $A_{dM,0}^{V}$
simultaneously features
$A_{dM,0}^{V}$
simultaneously features
![]() $\text{d}M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})/\text{d}\unicode[STIX]{x1D6FD}|_{\unicode[STIX]{x1D6FD}=\tilde{\unicode[STIX]{x1D6FD}}}=0$
and
$\text{d}M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})/\text{d}\unicode[STIX]{x1D6FD}|_{\unicode[STIX]{x1D6FD}=\tilde{\unicode[STIX]{x1D6FD}}}=0$
and
![]() $\tilde{\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D6FD}_{sat}$
. From pre-shock states in the dark-shaded region (enlarged area), uniformly stable non-ideal oblique shocks cannot occur. This region is bounded by the PSLL and the D’yakov–Kontorovich limit locus (DKLL).
$\tilde{\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D6FD}_{sat}$
. From pre-shock states in the dark-shaded region (enlarged area), uniformly stable non-ideal oblique shocks cannot occur. This region is bounded by the PSLL and the D’yakov–Kontorovich limit locus (DKLL).
Following the above considerations, the upper and lower pre-shock density limit for non-ideal post-shock Mach number profiles, along any given isentrope
![]() $s_{A}<s_{\unicode[STIX]{x1D70F}}$
, can be determined as follows:
$s_{A}<s_{\unicode[STIX]{x1D70F}}$
, can be determined as follows:
(i) the upper pre-shock density limit is either the high-density zero of
 $J_{A}$
along the selected isentrope or the saturation curve, if the selected isentrope enters the two-phase region and
$J_{A}$
along the selected isentrope or the saturation curve, if the selected isentrope enters the two-phase region and
 $J_{A}>0$
at the saturated vapour boundary;
$J_{A}>0$
at the saturated vapour boundary;(ii) with reference to figure 4, the lower pre-shock density limit corresponds to the pre-shock state leading either to the shock curve depicted in figure 4(a), which is characterized by
 $\text{d}M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD},\boldsymbol{A})/\text{d}\unicode[STIX]{x1D6FD}=0$
at
$\text{d}M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD},\boldsymbol{A})/\text{d}\unicode[STIX]{x1D6FD}=0$
at
 $\unicode[STIX]{x1D6FD}=\tilde{\unicode[STIX]{x1D6FD}}$
(
$\unicode[STIX]{x1D6FD}=\tilde{\unicode[STIX]{x1D6FD}}$
(
 $M_{B}=M_{A}$
), or to the shock curve in figure 4(b), where the post-shock state corresponding to
$M_{B}=M_{A}$
), or to the shock curve in figure 4(b), where the post-shock state corresponding to
 $M_{B}=M_{A}$
occurs on the saturation curve, namely
$M_{B}=M_{A}$
occurs on the saturation curve, namely
 $\tilde{\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D6FD}_{sat}$
on the limit curve;
$\tilde{\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D6FD}_{sat}$
on the limit curve;(iii) the conditions for acoustic emission may be satisfied within the complete non-ideal region
 $M_{B}>M_{A}$
of a shock curve, thus resulting in a narrower domain of pre-shock states for non-ideal oblique shocks that are uniformly stable against multidimensional perturbations. In the related limit shock curve, the transition from uniform to neutral stability occurs at
$M_{B}>M_{A}$
of a shock curve, thus resulting in a narrower domain of pre-shock states for non-ideal oblique shocks that are uniformly stable against multidimensional perturbations. In the related limit shock curve, the transition from uniform to neutral stability occurs at
 $\unicode[STIX]{x1D6FD}=\tilde{\unicode[STIX]{x1D6FD}}$
(
$\unicode[STIX]{x1D6FD}=\tilde{\unicode[STIX]{x1D6FD}}$
(
 $M_{B}=M_{A}$
), as shown in figure 4(c).
$M_{B}=M_{A}$
), as shown in figure 4(c).
By varying the reference isentrope, the existence domain of non-ideal oblique shocks as computed from the proposed procedure is shown in figure 5 for
![]() $M_{A}=2$
. The newly defined thermodynamic region is bounded by three different curves, which together define the so-called pre-shock limit locus (PSLL). Firstly, the portion of PSLL between point
$M_{A}=2$
. The newly defined thermodynamic region is bounded by three different curves, which together define the so-called pre-shock limit locus (PSLL). Firstly, the portion of PSLL between point
![]() $A_{V,1}^{J}$
, the high-density zero of
$A_{V,1}^{J}$
, the high-density zero of
![]() $J$
along the VLE line, and point
$J$
along the VLE line, and point
![]() $A_{\unicode[STIX]{x1D70F}}^{J}$
, for which the isentrope is tangent to the
$A_{\unicode[STIX]{x1D70F}}^{J}$
, for which the isentrope is tangent to the
![]() $J=0$
locus, is indeed coincident with the
$J=0$
locus, is indeed coincident with the
![]() $J=0$
locus. The branch included between
$J=0$
locus. The branch included between
![]() $A_{\unicode[STIX]{x1D70F}}^{J}$
and
$A_{\unicode[STIX]{x1D70F}}^{J}$
and
![]() $A_{dM,0}^{V}$
represents the locus of the limit pre-shock states resulting in shock curves featuring
$A_{dM,0}^{V}$
represents the locus of the limit pre-shock states resulting in shock curves featuring
![]() $\text{d}M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD},\boldsymbol{A})/\text{d}\unicode[STIX]{x1D6FD}=0$
when
$\text{d}M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD},\boldsymbol{A})/\text{d}\unicode[STIX]{x1D6FD}=0$
when
![]() $M_{B}=M_{A}$
(figure 4
a). At point
$M_{B}=M_{A}$
(figure 4
a). At point
![]() $A_{dM,0}^{V}$
, the shock curve simultaneously exhibits
$A_{dM,0}^{V}$
, the shock curve simultaneously exhibits
![]() $\text{d}M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD},\boldsymbol{A})/\text{d}\unicode[STIX]{x1D6FD}=0$
at
$\text{d}M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD},\boldsymbol{A})/\text{d}\unicode[STIX]{x1D6FD}=0$
at
![]() $\unicode[STIX]{x1D6FD}=\tilde{\unicode[STIX]{x1D6FD}}$
(
$\unicode[STIX]{x1D6FD}=\tilde{\unicode[STIX]{x1D6FD}}$
(
![]() $M_{B}=M_{A}$
) and
$M_{B}=M_{A}$
) and
![]() $\tilde{\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D6FD}_{sat}$
. The portion of the PSLL between point
$\tilde{\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D6FD}_{sat}$
. The portion of the PSLL between point
![]() $A_{dM,0}^{V}$
and
$A_{dM,0}^{V}$
and
![]() $A_{V,2}^{J}$
, the low-density zero of
$A_{V,2}^{J}$
, the low-density zero of
![]() $J$
along the VLE line, is obtained by collecting the limit pre-shock states for which
$J$
along the VLE line, is obtained by collecting the limit pre-shock states for which
![]() $\tilde{\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D6FD}_{sat}$
, that is, post-shock saturated conditions occur when
$\tilde{\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D6FD}_{sat}$
, that is, post-shock saturated conditions occur when
![]() $M_{B}=M_{A}$
(figure 4
b). Furthermore, the locus denoted as DKLL (D’yakov–Kontorovich limit locus) bounds a relatively small region (on its right-hand side) of pre-shock states leading to shock curves in which acoustic emission occurs over the entire
$M_{B}=M_{A}$
(figure 4
b). Furthermore, the locus denoted as DKLL (D’yakov–Kontorovich limit locus) bounds a relatively small region (on its right-hand side) of pre-shock states leading to shock curves in which acoustic emission occurs over the entire
![]() $\unicode[STIX]{x1D6FD}$
-range associated with
$\unicode[STIX]{x1D6FD}$
-range associated with
![]() $M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})>M_{A}$
. For pre-shock states in the right-hand side region of the DKLL, there does not exist uniformly stable non-ideal oblique shocks.
$M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD};\boldsymbol{A})>M_{A}$
. For pre-shock states in the right-hand side region of the DKLL, there does not exist uniformly stable non-ideal oblique shocks.
In the next section, the procedure outlined above is applied to the different fluids listed in table 1 to show its validity. Among the fluids considered, MDM, MM, octane, cyclopentane, toluene, benzene and R245fa all exhibit retrograde vapour boundaries; sulphur hexafluoride only exhibits a non-retrograde vapour boundary. The procedure for the computation of the existence domain of non-ideal oblique shocks in fluids having non-retrograde vapour boundaries is almost identical to that described above. When the saturated vapour boundary is non-retrograde, the shock curves centred on pre-shock states in the vapour phase cannot cross the two-phase region, thus remaining single phase. This implies that transitional shock curves of the type shown in figure 4(b) cannot occur. Therefore, with reference to the procedure outlined in the previous paragraph, the lower pre-shock density limit, along any given isentrope crossing the
![]() $J_{A}>0$
locus, is either the saturation curve or the pre-shock state leading to the transition depicted in figure 4(a).
$J_{A}>0$
locus, is either the saturation curve or the pre-shock state leading to the transition depicted in figure 4(a).
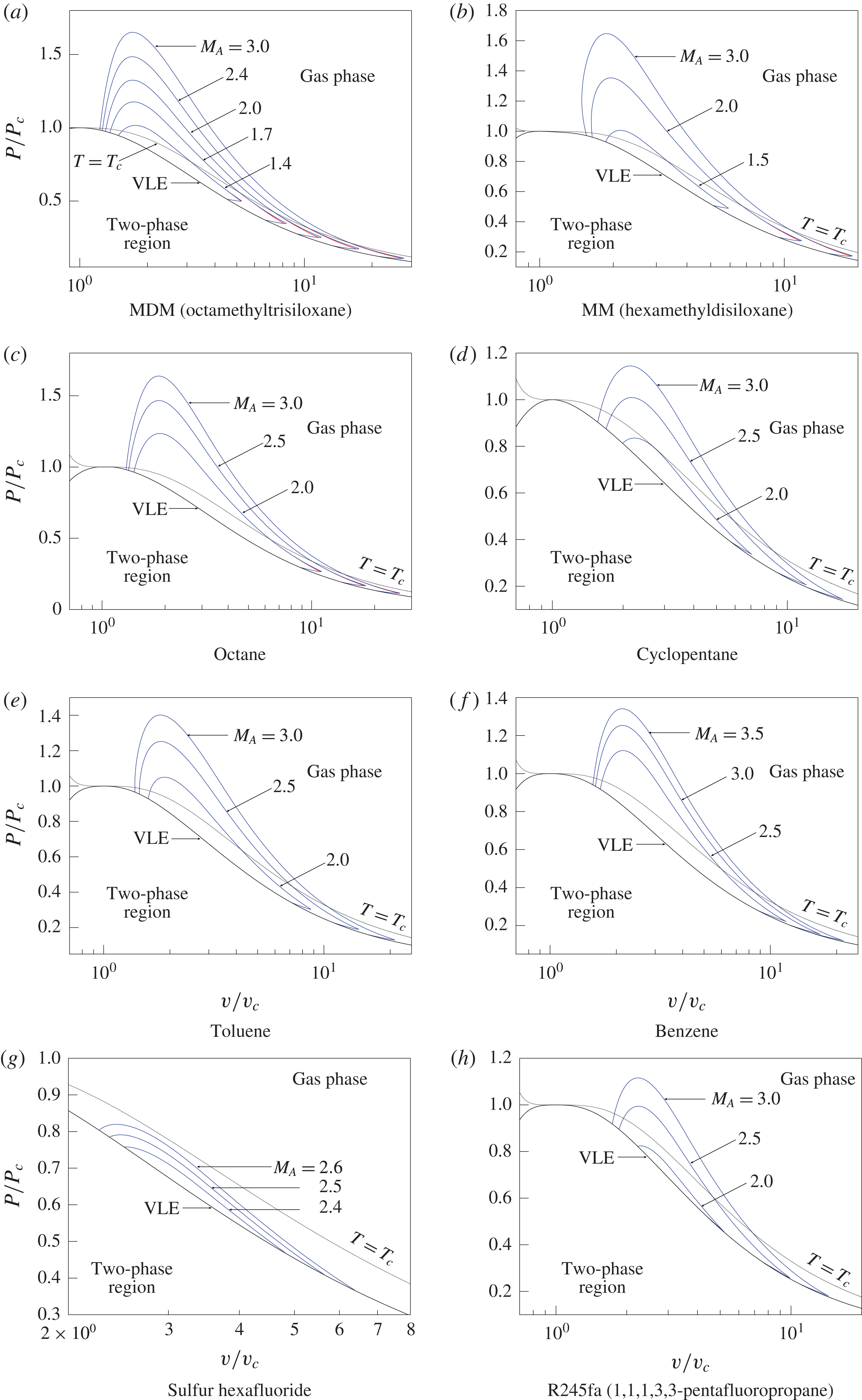
Figure 6. PSLL (blue line) and DKLL (red line) for different pre-shock Mach numbers, in each of the substances listed in table 1.
3.3 Results for selected substances
The procedure described in the previous section for MDM and one particular value of
![]() $M_{A}$
is applied here to the fluids listed in table 1 and the influence of
$M_{A}$
is applied here to the fluids listed in table 1 and the influence of
![]() $M_{A}$
is also evaluated. The Pre-shock limit loci and the D’yakov–Kontorovich limit loci in the selected fluids are reported, for different pre-shock Mach numbers, in figure 6(a–h). All the substances considered are endowed with a
$M_{A}$
is also evaluated. The Pre-shock limit loci and the D’yakov–Kontorovich limit loci in the selected fluids are reported, for different pre-shock Mach numbers, in figure 6(a–h). All the substances considered are endowed with a
![]() $\unicode[STIX]{x1D6E4}<1$
thermodynamic region. Moreover, for each of these fluids,
$\unicode[STIX]{x1D6E4}<1$
thermodynamic region. Moreover, for each of these fluids,
![]() ${\mathcal{K}}>0$
,
${\mathcal{K}}>0$
,
![]() $G>0$
and condition (2.15) is satisfied in the single-phase vapour region to which the present discussion is restricted. The selected siloxanes (cases a–b), hydrocarbons (cases b–f) and R234fa (case h) exhibit a retrograde portion of the saturated vapour boundary; accordingly, the corresponding pre-shock limit curves are qualitatively similar to those obtained in the previous section for MDM with
$G>0$
and condition (2.15) is satisfied in the single-phase vapour region to which the present discussion is restricted. The selected siloxanes (cases a–b), hydrocarbons (cases b–f) and R234fa (case h) exhibit a retrograde portion of the saturated vapour boundary; accordingly, the corresponding pre-shock limit curves are qualitatively similar to those obtained in the previous section for MDM with
![]() $M_{A}=2$
. On the other hand, sulphur hexafluoride (case g) exhibits a fairly simpler configuration as a result of its saturated vapour boundary being non-retrograde. In this case, according to the nomenclature used in figure 5, the portion of PSLL on the right-hand side of point
$M_{A}=2$
. On the other hand, sulphur hexafluoride (case g) exhibits a fairly simpler configuration as a result of its saturated vapour boundary being non-retrograde. In this case, according to the nomenclature used in figure 5, the portion of PSLL on the right-hand side of point
![]() $A_{\unicode[STIX]{x1D70F}}^{J}$
(comprising pre-shock states for shock curves featuring
$A_{\unicode[STIX]{x1D70F}}^{J}$
(comprising pre-shock states for shock curves featuring
![]() $\text{d}M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD},\boldsymbol{A})/\text{d}\unicode[STIX]{x1D6FD}=0$
when
$\text{d}M^{{\mathcal{H}}}(\unicode[STIX]{x1D6FD},\boldsymbol{A})/\text{d}\unicode[STIX]{x1D6FD}=0$
when
![]() $M_{B}=M_{A}$
) extends to a point on the VLE line.
$M_{B}=M_{A}$
) extends to a point on the VLE line.
It must be noticed that, among the configurations depicted in figure 6(a–g), only MDM, MM and octane exhibit limit curves for acoustic emission (DKLL), possibly owing to the lower values of
![]() $\unicode[STIX]{x1D6E4}_{min}$
and the larger extension of the region
$\unicode[STIX]{x1D6E4}_{min}$
and the larger extension of the region
![]() $\unicode[STIX]{x1D6E4}<1$
with respect to the other fluids considered here.
$\unicode[STIX]{x1D6E4}<1$
with respect to the other fluids considered here.
The influence of the pre-shock Mach number on the shape and extension of the pre-shock state region for non-ideal oblique shock waves, which can be appreciated from figure 6(a–g), can be commented as follows. Firstly, there exist a minimum threshold of the pre-shock Mach number
![]() $M_{A,min}=(1-\unicode[STIX]{x1D6E4}_{min})^{-1/2}$
, below which non-ideal oblique shocks cannot occur. This amounts to requiring that
$M_{A,min}=(1-\unicode[STIX]{x1D6E4}_{min})^{-1/2}$
, below which non-ideal oblique shocks cannot occur. This amounts to requiring that
![]() $\unicode[STIX]{x1D6E4}<1-1/M_{A}^{2}$
somewhere in the single-phase vapour region. The condition
$\unicode[STIX]{x1D6E4}<1-1/M_{A}^{2}$
somewhere in the single-phase vapour region. The condition
![]() $\unicode[STIX]{x1D6E4}<1-1/M_{A}^{2}$
is necessary for the existence of non-ideal oblique shocks having pre-shock Mach number
$\unicode[STIX]{x1D6E4}<1-1/M_{A}^{2}$
is necessary for the existence of non-ideal oblique shocks having pre-shock Mach number
![]() $M_{A}$
. Indeed, assuming
$M_{A}$
. Indeed, assuming
![]() $G>0$
,
$G>0$
,
![]() ${\mathcal{K}}>0$
and that (2.15) holds,
${\mathcal{K}}>0$
and that (2.15) holds,
![]() $J_{B}>0$
must be satisfied somewhere along the shock curve in order that the post-shock Mach number is non-decreasing, see equation (2.17). Unless
$J_{B}>0$
must be satisfied somewhere along the shock curve in order that the post-shock Mach number is non-decreasing, see equation (2.17). Unless
![]() $J_{B}>0$
holds in the acoustic limit (namely
$J_{B}>0$
holds in the acoustic limit (namely
![]() $J_{A}>0$
and
$J_{A}>0$
and
![]() $M_{B}>M_{A}$
for weak oblique shocks),
$M_{B}>M_{A}$
for weak oblique shocks),
![]() $J_{B}>0$
must be satisfied when
$J_{B}>0$
must be satisfied when
![]() $M_{B}<M_{A}$
. Both cases clearly imply that
$M_{B}<M_{A}$
. Both cases clearly imply that
![]() $\unicode[STIX]{x1D6E4}<1-1/M_{A}^{2}$
somewhere in the thermodynamic state space. With increasing values of the pre-shock Mach number, the size of the pre-shock state domain for non-ideal oblique shocks increases (as the size of the
$\unicode[STIX]{x1D6E4}<1-1/M_{A}^{2}$
somewhere in the thermodynamic state space. With increasing values of the pre-shock Mach number, the size of the pre-shock state domain for non-ideal oblique shocks increases (as the size of the
![]() $J_{A}>0$
region does), whereas its shape remains qualitatively unchanged. In this respect, the size of
$J_{A}>0$
region does), whereas its shape remains qualitatively unchanged. In this respect, the size of
![]() $\unicode[STIX]{x1D6E4}$
isolines (and thus of
$\unicode[STIX]{x1D6E4}$
isolines (and thus of
![]() $J=0$
loci for fixed
$J=0$
loci for fixed
![]() $M_{A}$
, which roughly coincides with the newly defined thermodynamic domain) of most pure fluids increases with
$M_{A}$
, which roughly coincides with the newly defined thermodynamic domain) of most pure fluids increases with
![]() $\unicode[STIX]{x1D6E4}$
(see, e.g. Colonna, Guardone & Nannan Reference Colonna, Guardone and Nannan2007, for siloxanes). More in general, the qualitative trend of the fundamental derivative in the single-phase vapour region of all fluids having regions
$\unicode[STIX]{x1D6E4}$
(see, e.g. Colonna, Guardone & Nannan Reference Colonna, Guardone and Nannan2007, for siloxanes). More in general, the qualitative trend of the fundamental derivative in the single-phase vapour region of all fluids having regions
![]() $\unicode[STIX]{x1D6E4}<1$
agrees with the predictions of the simple van der Waals model (see, e.g. Thompson & Lambrakis Reference Thompson and Lambrakis1973), which in turn are consistent with the results obtained in the present section. The latter claim leads us expect that the present findings are arguably valid for most single-phase fluids exhibiting
$\unicode[STIX]{x1D6E4}<1$
agrees with the predictions of the simple van der Waals model (see, e.g. Thompson & Lambrakis Reference Thompson and Lambrakis1973), which in turn are consistent with the results obtained in the present section. The latter claim leads us expect that the present findings are arguably valid for most single-phase fluids exhibiting
![]() $\unicode[STIX]{x1D6E4}<1$
in the vapour region.
$\unicode[STIX]{x1D6E4}<1$
in the vapour region.
4 Conclusions
Non-ideal oblique shock waves, featuring an increase of the value of the flow Mach number across the discontinuity, were investigated in the context of single-phase vapour flows of fluids exhibiting positive nonlinearity. The increase of the Mach number results from the decrease of the speed of sound across the shock wave, which is predicted to be possible only in the non-ideal gas dynamic regime of fluids characterized by moderate-to-high molecular complexity.
By examining oblique shocks in the
![]() $M_{B}$
–
$M_{B}$
–
![]() $\unicode[STIX]{x1D6FD}$
plane, the different scenarios for the observation of Mach number increasing configurations were identified, pointing out the roles of the pre-shock thermodynamic quantities and Mach number. Considerations of multidimensional shock stability, in terms of D’yakov–Kontorovich conditions for acoustic emission or neutral stability to transverse perturbations of the shock front, were also given.
$\unicode[STIX]{x1D6FD}$
plane, the different scenarios for the observation of Mach number increasing configurations were identified, pointing out the roles of the pre-shock thermodynamic quantities and Mach number. Considerations of multidimensional shock stability, in terms of D’yakov–Kontorovich conditions for acoustic emission or neutral stability to transverse perturbations of the shock front, were also given.
In the parameter space associated with the pre-shock state variables (thermodynamic quantities and Mach number), the flow conditions leading to the occurrence of non-ideal oblique shocks were singled out. As a result, a family of thermodynamic regions, parametrized by the pre-shock Mach number
![]() $M_{A}$
, was introduced. For a given value of
$M_{A}$
, was introduced. For a given value of
![]() $M_{A}$
, the newly defined regions embed all the pre-shock thermodynamic states from which non-ideal oblique shocks can possibly occur. The computational procedure for determining the admissibility domain of non-ideal oblique shocks was first illustrated using siloxane MDM and subsequently applied to other fluids, yielding consistent results. For each of the fluids considered, state-of-the-art thermodynamic models were used.
$M_{A}$
, the newly defined regions embed all the pre-shock thermodynamic states from which non-ideal oblique shocks can possibly occur. The computational procedure for determining the admissibility domain of non-ideal oblique shocks was first illustrated using siloxane MDM and subsequently applied to other fluids, yielding consistent results. For each of the fluids considered, state-of-the-art thermodynamic models were used.
The present analysis is valid under the hypotheses that, in the single-phase vapour region, (i) the specific volume monotonically decreases with shock strength along the compression branch of the Hugoniot locus, (ii) the Grüneisen coefficient is positive and (iii) the speed of sound increases with the entropy at constant volume. These conditions are arguably not limiting, insofar as they are verified for most vapours of practical interest. Under the above assumptions, it was shown that a necessary condition for the occurrence of non-ideal oblique shock waves is that a thermodynamic region featuring fundamental derivative
![]() $\unicode[STIX]{x1D6E4}<1$
exists. In particular, for any given pre-shock Mach number
$\unicode[STIX]{x1D6E4}<1$
exists. In particular, for any given pre-shock Mach number
![]() $M_{A}$
, it is required that
$M_{A}$
, it is required that
![]() $\unicode[STIX]{x1D6E4}<1-1/M_{A}^{2}$
somewhere in the thermodynamic state space. Therefore, the present findings arguably apply to most vapours exhibiting
$\unicode[STIX]{x1D6E4}<1-1/M_{A}^{2}$
somewhere in the thermodynamic state space. Therefore, the present findings arguably apply to most vapours exhibiting
![]() $\unicode[STIX]{x1D6E4}<1$
and are expected to be relevant for various non-ideal compressible-fluid applications including Organic Rankine Cycle power systems, high-enthalpy flows in wind tunnels and space propulsion.
$\unicode[STIX]{x1D6E4}<1$
and are expected to be relevant for various non-ideal compressible-fluid applications including Organic Rankine Cycle power systems, high-enthalpy flows in wind tunnels and space propulsion.
Acknowledgement
This research is supported by ERC Consolidator Grant N. 617603, Project NSHOCK, funded under the FP7-IDEAS-ERC scheme.












