Research Article
Semi-field-like affine planes
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 113-123
-
- Article
-
- You have access
- Export citation
A reflection principle for solutions to the Helmholtz equation and an application to the inverse scattering problem†
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 125-130
-
- Article
-
- You have access
- Export citation
Representations of the ℓ1-algebra of an inverse semigroup having the separation property†
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 131-143
-
- Article
-
- You have access
- Export citation
Topological groups with co-monoid structures
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 145-152
-
- Article
-
- You have access
- Export citation
The reckoning of certain quartic and octic Gauss sums
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 153-155
-
- Article
-
- You have access
- Export citation
A note on regular local Noether lattices II
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 157-159
-
- Article
-
- You have access
- Export citation
A Lyapunov inequality and forced oscillations in general nonlinear nth order differential-difference equations†
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 161-166
-
- Article
-
- You have access
- Export citation
Conjugacy in groups with dihedral 3-normalisers
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 167-173
-
- Article
-
- You have access
- Export citation
On a dual integral equation with a trigonometric kernel
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 175-177
-
- Article
-
- You have access
- Export citation
A remark on the generalized numerical range of a normal matrix
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 179-180
-
- Article
-
- You have access
- Export citation
Congruences on an orthodox semigroup via the minimum inverse semigroup congruence
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 181-192
-
- Article
-
- You have access
- Export citation
Grothendieck groups of twisted free associative algebras
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 193-196
-
- Article
-
- You have access
- Export citation
Commutators and normal operators
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 197-198
-
- Article
-
- You have access
- Export citation
Embedding inverse semigroups of homeomorphisms on closed subsets
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 199-207
-
- Article
-
- You have access
- Export citation
Front matter
GMJ volume 18 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
GMJ volume 18 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 May 2009, p. b1
-
- Article
-
- You have access
- Export citation



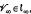 the line at infinity of
the line at infinity of 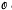 the subgroup
the subgroup 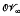 Note also that since
Note also that since 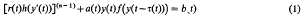
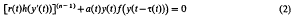


 (
( = {α
= {α {
{