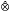Research Article
Primes of the form [pc] and related questions
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 131-141
-
- Article
-
- You have access
- Export citation
Modulus of nearly uniform smoothness and Lindenstrauss formulae
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 143-153
-
- Article
-
- You have access
- Export citation
Right fully idempotent rings need not be left fully idempotent
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 155-157
-
- Article
-
- You have access
- Export citation
A Mayer-Vietoris sequence in group homology and the decomposition of relation modules
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 159-171
-
- Article
-
- You have access
- Export citation
On the endomorphism semigroup of an ordered set
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 173-178
-
- Article
-
- You have access
- Export citation
Singular pleated surfaces and CP1–structures
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 179-190
-
- Article
-
- You have access
- Export citation
Injective homogeneity and the Auslander–Gorenstein property
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 191-204
-
- Article
-
- You have access
- Export citation
On group graded rings satisfying polynomial identities
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 205-210
-
- Article
-
- You have access
- Export citation
Polynomial Grothendieck properties
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 211-219
-
- Article
-
- You have access
- Export citation
Minimum topological genus of compact bordered Klein surfaces admitting a prime-power automorphism
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 221-232
-
- Article
-
- You have access
- Export citation
Null 2-type Chen surfaces
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 233-242
-
- Article
-
- You have access
- Export citation
Outer automorphisms of hypercentral p-groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 243-247
-
- Article
-
- You have access
- Export citation
Skew group rings and maximal orders
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 249-263
-
- Article
-
- You have access
- Export citation
Front matter
GMJ volume 37 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
GMJ volume 37 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation



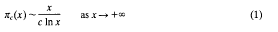
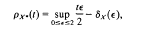
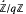 /q for any non-negative integer
/q for any non-negative integer 
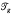 be the Teichmuller space of
be the Teichmuller space of 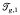 the space of marked hyperbolic structures on
the space of marked hyperbolic structures on 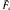
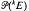 (
(