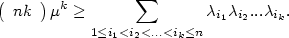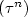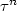Research Article
Comparison of order statistics in a random sequence to the same statistics with i.i.d. variables
-
- Published online by Cambridge University Press:
- 16 December 2005, pp. 1-10
-
- Article
- Export citation
Using auxiliary information in statistical function estimation
-
- Published online by Cambridge University Press:
- 16 December 2005, pp. 11-23
-
- Article
- Export citation
How many bins should be put in a regular histogram
-
- Published online by Cambridge University Press:
- 31 January 2006, pp. 24-45
-
- Article
- Export citation
Adaptive tests for periodic signal detection with applications to laser vibrometry
-
- Published online by Cambridge University Press:
- 31 January 2006, pp. 46-75
-
- Article
- Export citation
Dynamiques recuites de type Feynman-Kac : résultats précis et conjectures
-
- Published online by Cambridge University Press:
- 09 March 2006, pp. 76-140
-
- Article
- Export citation
Stability of solutions of BSDEs with random terminal time
-
- Published online by Cambridge University Press:
- 09 March 2006, pp. 141-163
-
- Article
- Export citation
Model selection for estimating the non zero components of a Gaussian vector
-
- Published online by Cambridge University Press:
- 09 March 2006, pp. 164-183
-
- Article
- Export citation
Forward-backward stochastic differential equations and PDE with gradient dependent second order coefficients
-
- Published online by Cambridge University Press:
- 09 March 2006, pp. 184-205
-
- Article
- Export citation
Preservation of log-concavity on summation
-
- Published online by Cambridge University Press:
- 03 May 2006, pp. 206-215
-
- Article
- Export citation
Bootstrapping the shorth for regression
-
- Published online by Cambridge University Press:
- 03 May 2006, pp. 216-235
-
- Article
- Export citation
Branching random motions, nonlinear hyperbolic systems and travellind waves
-
- Published online by Cambridge University Press:
- 03 May 2006, pp. 236-257
-
- Article
- Export citation
On the Brunk-Chung type strong law of large numbers for sequences of blockwise m-dependent random variables
-
- Published online by Cambridge University Press:
- 03 May 2006, pp. 258-268
-
- Article
- Export citation
Stein estimation for infinitely divisible laws
-
- Published online by Cambridge University Press:
- 08 September 2006, pp. 269-276
-
- Article
- Export citation
Cyclic random motions in $\mathbb{R}^d$
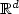 -space with
n directions
-space with
n directions
-
- Published online by Cambridge University Press:
- 08 September 2006, pp. 277-316
-
- Article
- Export citation
Binomial-Poisson entropic inequalities and the M/M/∞ queue
-
- Published online by Cambridge University Press:
- 08 September 2006, pp. 317-339
-
- Article
- Export citation
Nearest neighbor classification in infinite dimension
-
- Published online by Cambridge University Press:
- 08 September 2006, pp. 340-355
-
- Article
- Export citation
Stochastic differential equations driven by processes generated by divergence form operators I: a Wong-Zakai theorem
-
- Published online by Cambridge University Press:
- 08 September 2006, pp. 356-379
-
- Article
- Export citation
SPDEs with coloured noise: Analytic and stochastic approaches
-
- Published online by Cambridge University Press:
- 20 October 2006, pp. 380-405
-
- Article
- Export citation