Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Fromont, Magalie
and
Tuleau, Christine
2006.
Learning Theory.
Vol. 4005,
Issue. ,
p.
94.
Cuevas, Antonio
Febrero, Manuel
and
Fraiman, Ricardo
2007.
Robust estimation and classification for functional data via projection-based depth notions.
Computational Statistics,
Vol. 22,
Issue. 3,
p.
481.
Baíllo, Amparo
and
Cuevas, Antonio
2008.
Functional and Operatorial Statistics.
p.
43.
Burba, Florent
Ferraty, Frédéric
and
Vieu, Philippe
2008.
Convergence de l'estimateur à noyau des k plus proches voisins en régression fonctionnelle non-paramétrique.
Comptes Rendus Mathematique,
Vol. 346,
Issue. 5-6,
p.
339.
Laloë, Thomas
2008.
A k-nearest neighbor approach for functional regression.
Statistics & Probability Letters,
Vol. 78,
Issue. 10,
p.
1189.
Porro, Diana
Duin, Robert W.
Talavera, Isneri
and
Hdez, Noslen
2009.
Progress in Pattern Recognition, Image Analysis, Computer Vision, and Applications.
Vol. 5856,
Issue. ,
p.
513.
Biau, Gérard
Cerou, Frédéric
and
Guyader, Arnaud
2010.
Rates of Convergence of the Functional $k$-Nearest Neighbor Estimate.
IEEE Transactions on Information Theory,
Vol. 56,
Issue. 4,
p.
2034.
Llop, P.
Forzani, L.
and
Fraiman, R.
2011.
On local times, density estimation and supervised classification from functional data.
Journal of Multivariate Analysis,
Vol. 102,
Issue. 1,
p.
73.
Porro‐Muñoz, Diana
Talavera, Isneri
Duin, Robert P. W.
Hernández, Noslen
and
Orozco‐Alzate, Mauricio
2011.
Dissimilarity representation on functional spectral data for classification.
Journal of Chemometrics,
Vol. 25,
Issue. 9,
p.
476.
BAÍLLO, AMPARO
CUEVAS, ANTONIO
and
CUESTA‐ALBERTOS, JUAN ANTONIO
2011.
Supervised Classification for a Family of Gaussian Functional Models.
Scandinavian Journal of Statistics,
Vol. 38,
Issue. 3,
p.
480.
Forzani, Liliana
Fraiman, Ricardo
and
Llop, Pamela
2012.
Consistent Nonparametric Regression for Functional Data Under the Stone–Besicovitch Conditions.
IEEE Transactions on Information Theory,
Vol. 58,
Issue. 11,
p.
6697.
Pestov, Vladimir
2013.
Is thek-NN classifier in high dimensions affected by the curse of dimensionality?.
Computers & Mathematics with Applications,
Vol. 65,
Issue. 10,
p.
1427.
Sguera, Carlo
Galeano, Pedro
and
Lillo, Rosa
2014.
Spatial depth-based classification for functional data.
TEST,
Vol. 23,
Issue. 4,
p.
725.
Cuevas, Antonio
2014.
A partial overview of the theory of statistics with functional data.
Journal of Statistical Planning and Inference,
Vol. 147,
Issue. ,
p.
1.
Biau, Gérard
and
Devroye, Luc
2015.
Lectures on the Nearest Neighbor Method.
p.
241.
Biau, Gérard
and
Devroye, Luc
2015.
Lectures on the Nearest Neighbor Method.
p.
131.
Biau, Gérard
and
Devroye, Luc
2015.
Lectures on the Nearest Neighbor Method.
p.
3.
Biau, Gérard
and
Devroye, Luc
2015.
Lectures on the Nearest Neighbor Method.
p.
223.
Biau, Gérard
and
Devroye, Luc
2015.
Lectures on the Nearest Neighbor Method.
p.
33.
Biau, Gérard
and
Devroye, Luc
2015.
Lectures on the Nearest Neighbor Method.
p.
95.
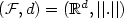 ,
Stone (1977) proved in 1977 the universal consistency of this classifier:
its probability of error converges to the Bayes error, whatever the
distribution of (X,Y). We show in this paper that this result is no
longer valid in general metric spaces. However, if (F,d) is
separable and if some regularity condition is assumed, then the
k-nearest neighbor classifier is weakly consistent.
,
Stone (1977) proved in 1977 the universal consistency of this classifier:
its probability of error converges to the Bayes error, whatever the
distribution of (X,Y). We show in this paper that this result is no
longer valid in general metric spaces. However, if (F,d) is
separable and if some regularity condition is assumed, then the
k-nearest neighbor classifier is weakly consistent.




