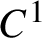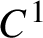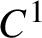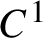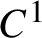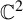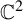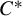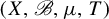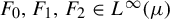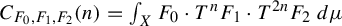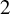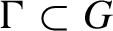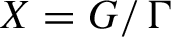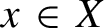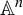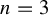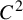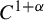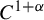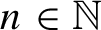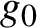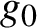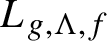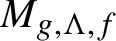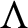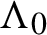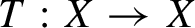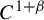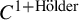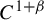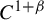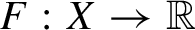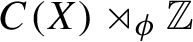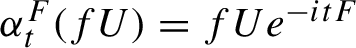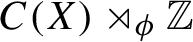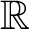Original Article
Anatole Katok
- Part of:
-
- Published online by Cambridge University Press:
- 04 October 2021, pp. 321-388
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Accessibility and centralizers for partially hyperbolic flows
- Part of:
-
- Published online by Cambridge University Press:
- 11 May 2021, pp. 835-854
-
- Article
- Export citation
Normal forms for strong magnetic systems on surfaces: trapping regions and rigidity of Zoll systems
- Part of:
-
- Published online by Cambridge University Press:
- 22 March 2021, pp. 1871-1897
-
- Article
-
- You have access
- Open access
- Export citation
Mixing operators with prescribed unimodular eigenvalues
- Part of:
-
- Published online by Cambridge University Press:
- 28 December 2020, pp. 1-8
-
- Article
- Export citation
Topological and geometric hyperbolicity criteria for polynomial automorphisms of
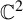 ${\mathbb {C}^2}$
${\mathbb {C}^2}$
- Part of:
-
- Published online by Cambridge University Press:
- 04 May 2021, pp. 2151-2171
-
- Article
-
- You have access
- Open access
- Export citation
Partial C*-dynamics and Rokhlin dimension
-
- Published online by Cambridge University Press:
- 03 August 2021, pp. 2991-3024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Anosov diffeomorphisms, anisotropic BV spaces and regularity of foliations
- Part of:
-
- Published online by Cambridge University Press:
- 04 June 2021, pp. 2431-2467
-
- Article
-
- You have access
- Open access
- Export citation
On the dimension of points which escape to infinity at given rate under exponential iteration
- Part of:
-
- Published online by Cambridge University Press:
- 29 March 2021, pp. 1591-1623
-
- Article
- Export citation
Multiple correlation sequences not approximable by nilsequences
- Part of:
-
- Published online by Cambridge University Press:
- 16 July 2021, pp. 2711-2722
-
- Article
- Export citation
Non-dense orbits on homogeneous spaces and applications to geometry and number theory
- Part of:
-
- Published online by Cambridge University Press:
- 18 March 2021, pp. 1327-1372
-
- Article
- Export citation
Dynamical degrees of affine-triangular automorphisms of affine spaces
- Part of:
-
- Published online by Cambridge University Press:
- 01 October 2021, pp. 3551-3592
-
- Article
- Export citation
Quasisymmetric orbit-flexibility of multicritical circle maps
- Part of:
-
- Published online by Cambridge University Press:
- 30 September 2021, pp. 3271-3310
-
- Article
- Export citation
Reconstructing a minimal topological dynamical system from a set of return times
- Part of:
-
- Published online by Cambridge University Press:
- 03 September 2021, pp. 2723-2739
-
- Article
- Export citation
Lee-Yang zeros of the antiferromagnetic Ising model
- Part of:
-
- Published online by Cambridge University Press:
- 08 April 2021, pp. 2172-2206
-
- Article
-
- You have access
- Open access
- Export citation
Examples of distorted interval diffeomorphisms of intermediate regularity
- Part of:
-
- Published online by Cambridge University Press:
- 08 September 2021, pp. 3311-3324
-
- Article
- Export citation
Ergodic cocycles of IDPFT systems and non-singular Gaussian actions
- Part of:
-
- Published online by Cambridge University Press:
- 18 February 2021, pp. 1624-1654
-
- Article
- Export citation
Continuity of Hausdorff dimension across generic dynamical Lagrange and Markov spectra II
- Part of:
-
- Published online by Cambridge University Press:
- 22 April 2021, pp. 1898-1907
-
- Article
- Export citation
Uniformly positive entropy of induced transformations
- Part of:
-
- Published online by Cambridge University Press:
- 28 December 2020, pp. 9-18
-
- Article
- Export citation
Smoothness of stable holonomies inside center-stable manifolds
- Part of:
-
- Published online by Cambridge University Press:
- 18 October 2021, pp. 3593-3618
-
- Article
- Export citation
KMS states on the crossed product
 $C^*$
-algebra of a homeomorphism
$C^*$
-algebra of a homeomorphism
- Part of:
-
- Published online by Cambridge University Press:
- 15 February 2021, pp. 1373-1414
-
- Article
- Export citation