Article contents
Smoothness of stable holonomies inside center-stable manifolds
Published online by Cambridge University Press: 18 October 2021
Abstract
Under a suitable bunching condition, we establish that stable holonomies inside center-stable manifolds for 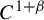 $C^{1+\beta }$
diffeomorphisms are uniformly bi-Lipschitz and, in fact,
$C^{1+\beta }$
diffeomorphisms are uniformly bi-Lipschitz and, in fact, 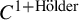 $C^{1+\mathrm {H}\ddot{\rm o}\mathrm {lder}}$
. This verifies the ergodicity of suitably center-bunched, essentially accessible, partially hyperbolic
$C^{1+\mathrm {H}\ddot{\rm o}\mathrm {lder}}$
. This verifies the ergodicity of suitably center-bunched, essentially accessible, partially hyperbolic 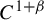 $C^{1+\beta }$
diffeomorphisms and verifies that the Ledrappier–Young entropy formula holds for
$C^{1+\beta }$
diffeomorphisms and verifies that the Ledrappier–Young entropy formula holds for 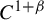 $C^{1+\beta }$
diffeomorphisms of compact manifolds.
$C^{1+\beta }$
diffeomorphisms of compact manifolds.
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 3
- Cited by





