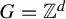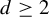1. Introduction
Our central question is as follows. Given subshifts X and Y over a countable amenable group G, under what conditions does X embed into Y? That is, under what conditions is X isomorphic to a subsystem of Y? One necessary condition is that
![]() $h(X) \leq h(Y)$
, where
$h(X) \leq h(Y)$
, where
![]() $h(X)$
is the topological entropy of the subshift X (Definition 2.11), because topological entropy is preserved under isomorphism and non-increasing under taking subsystems. When
$h(X)$
is the topological entropy of the subshift X (Definition 2.11), because topological entropy is preserved under isomorphism and non-increasing under taking subsystems. When
![]() $G = \mathbb {Z}$
, the classical embedding theorem of Krieger [Reference Krieger13, Theorem 3] provides a complete answer in the case that Y is a mixing shift of finite type (SFT) and
$G = \mathbb {Z}$
, the classical embedding theorem of Krieger [Reference Krieger13, Theorem 3] provides a complete answer in the case that Y is a mixing shift of finite type (SFT) and
![]() $h(X) < h(Y)$
. Namely, a certain necessary condition about periodic points turns out to be sufficient for an embedding
$h(X) < h(Y)$
. Namely, a certain necessary condition about periodic points turns out to be sufficient for an embedding
![]() $\psi : X \to Y$
to exist. In particular, the condition is automatically satisfied if X is strongly aperiodic (Definition 2.8), meaning that no point of X exhibits a non-identity element of G as a period (in other words, the shift action is free on X). Krieger’s embedding theorem has become a cornerstone of the structure theory of SFTs over
$\psi : X \to Y$
to exist. In particular, the condition is automatically satisfied if X is strongly aperiodic (Definition 2.8), meaning that no point of X exhibits a non-identity element of G as a period (in other words, the shift action is free on X). Krieger’s embedding theorem has become a cornerstone of the structure theory of SFTs over
![]() $\mathbb {Z}$
.
$\mathbb {Z}$
.
Much less is known about the embedding problem for groups other than
![]() $G = \mathbb {Z}$
. In the case where
$G = \mathbb {Z}$
. In the case where
![]() $G = \mathbb {Z}^d$
for
$G = \mathbb {Z}^d$
for
![]() $d\geq 2$
, one result is given by Lightwood: suppose X is a strongly aperiodic subshift and suppose Y is an SFT that satisfies a mixing condition (‘square mixing’, known elsewhere as the ‘uniform filling’ property) and contains a point with a finite orbit. If
$d\geq 2$
, one result is given by Lightwood: suppose X is a strongly aperiodic subshift and suppose Y is an SFT that satisfies a mixing condition (‘square mixing’, known elsewhere as the ‘uniform filling’ property) and contains a point with a finite orbit. If
![]() $h(X) < h(Y)$
and Y contains at least one factor of X (an image of X under a continuous and shift-commuting map), then X embeds into Y [Reference Lightwood14, Theorem 2.5]. Lightwood also proved that in the case where
$h(X) < h(Y)$
and Y contains at least one factor of X (an image of X under a continuous and shift-commuting map), then X embeds into Y [Reference Lightwood14, Theorem 2.5]. Lightwood also proved that in the case where
![]() $G = \mathbb {Z}^2$
, a square mixing SFT automatically contains a point with a finite orbit [Reference Lightwood14, Lemma 9.2]. Later, Lightwood proved that if Y is an SFT over
$G = \mathbb {Z}^2$
, a square mixing SFT automatically contains a point with a finite orbit [Reference Lightwood14, Lemma 9.2]. Later, Lightwood proved that if Y is an SFT over
![]() $\mathbb {Z}^2$
satisfying a slightly stronger mixing condition (‘square-filling mixing’, which implies square mixing), then Y automatically contains at least one factor of X [Reference Lightwood15, Theorem 2.8]. These results together provide a partial extension of Krieger’s embedding theorem to
$\mathbb {Z}^2$
satisfying a slightly stronger mixing condition (‘square-filling mixing’, which implies square mixing), then Y automatically contains at least one factor of X [Reference Lightwood15, Theorem 2.8]. These results together provide a partial extension of Krieger’s embedding theorem to
![]() $G = \mathbb {Z}^2$
.
$G = \mathbb {Z}^2$
.
In this paper, we obtain an embedding theorem for subshifts over countable amenable groups with the comparison property. We do not define the comparison property here, but we appeal to it in the form of Theorem 2.10, a consequence of the comparison property due to Downarowicz and Zhang [Reference Downarowicz and Zhang8, Reference Downarowicz and Zhang9]. We also note that the class of amenable groups with the comparison property includes every countable group containing no finitely generated subgroup of exponential growth (proof given in both [Reference Downarowicz and Zhang9, Theorem 5.11] and [Reference Downarowicz and Zhang8, Theorem 6.33]). In particular, this includes every countable abelian group. It is unknown whether there exists a countable amenable group without the comparison property.
Our main result is as follows.
Theorem 3.5. Let G be a countable amenable group with the comparison property. Let X be a non-empty strongly aperiodic subshift over G. Let Y be a strongly irreducible SFT over G with no global period. If
![]() $h(X) < h(Y)$
and Y contains at least one factor of X, then X embeds into Y.
$h(X) < h(Y)$
and Y contains at least one factor of X, then X embeds into Y.
If one selects
![]() $G = \mathbb {Z}^d$
for
$G = \mathbb {Z}^d$
for
![]() $d\geq 2$
in the above statement, then one does not immediately recover the theorem of Lightwood. We assume here a slightly stronger mixing condition on Y (strong irreducibility in place of square mixing). However, we do not assume that Y contains a point with a finite orbit; instead, we assume that Y has no global period, a condition that is automatically true for strongly irreducible subshifts over
$d\geq 2$
in the above statement, then one does not immediately recover the theorem of Lightwood. We assume here a slightly stronger mixing condition on Y (strong irreducibility in place of square mixing). However, we do not assume that Y contains a point with a finite orbit; instead, we assume that Y has no global period, a condition that is automatically true for strongly irreducible subshifts over
![]() $\mathbb {Z}^d$
.
$\mathbb {Z}^d$
.
In the following paragraphs, we briefly discuss the hypotheses of the above theorem and how they are invoked in the proof.
The condition that Y has no global period means that the shift action is faithful on Y. This condition is examined in detail in §3.1. This condition is necessary for the theorem; in particular, if a non-empty strongly aperiodic subshift X embeds into Y, then Y exhibits an aperiodic point and therefore has no global period.
The condition that X is strongly aperiodic allows us to derive systems of useful quasi-tilings (Definition 2.14) of the group G as factors of X, by appealing to a theorem of Downarowicz and Huczek [Reference Downarowicz and Huczek6, Lemma 3.4]. The strong aperiodicity is necessary for this; indeed, if X factors onto systems of quasi-tilings with arbitrarily large, disjoint tiles, then no point of X can exhibit a non-trivial period. The comparison property allows us to go one step further and derive from X systems of useful exact tilings of the group G. We accomplish this by adapting a construction of Downarowicz and Zhang (presented in both [Reference Downarowicz and Zhang9, Theorem 6.3] and [Reference Downarowicz and Zhang8, Theorem 7.5]).
The condition that
![]() $h(X) < h(Y)$
allows us to deduce that if a finite subset (namely, the shape of a tile in a given quasi-tiling) is large enough, then there are more patterns of that shape appearing in points of Y than in X. This implies that there is an injective map from tile patterns in X to tile patterns in Y. The condition that Y is a strongly irreducible SFT allows us to mix those tile patterns together into a single point of Y.
$h(X) < h(Y)$
allows us to deduce that if a finite subset (namely, the shape of a tile in a given quasi-tiling) is large enough, then there are more patterns of that shape appearing in points of Y than in X. This implies that there is an injective map from tile patterns in X to tile patterns in Y. The condition that Y is a strongly irreducible SFT allows us to mix those tile patterns together into a single point of Y.
The condition that Y contains a factor of X means that there exists a continuous and shift-commuting map (a homomorphism)
![]() $\phi : X\to Y$
, though not necessarily one that is injective. This is of course necessary for the theorem, since an embedding is a homomorphism, but the existence of a possibly non-injective homomorphism is a useful condition and one that is much easier to attain. It is automatically satisfied if, for instance, Y contains a fixed point. We use the homomorphism
$\phi : X\to Y$
, though not necessarily one that is injective. This is of course necessary for the theorem, since an embedding is a homomorphism, but the existence of a possibly non-injective homomorphism is a useful condition and one that is much easier to attain. It is automatically satisfied if, for instance, Y contains a fixed point. We use the homomorphism
![]() $\phi $
in our construction to code the boundary regions of the tiles in a given tiling, as well as the region of G not covered by any tile.
$\phi $
in our construction to code the boundary regions of the tiles in a given tiling, as well as the region of G not covered by any tile.
The condition that Y has no global period allows marker patterns to be constructed in Y (Theorem 3.4), which are used to encode the locations of the centers of the tiles of a given quasi-tiling within a controllably sparse subset of the symbols of a point of Y. This extends the approach of Lightwood [Reference Lightwood14] who constructed marker patterns for
![]() $G = \mathbb {Z}^d$
; the concept originates in the work of Krieger and Boyle for
$G = \mathbb {Z}^d$
; the concept originates in the work of Krieger and Boyle for
![]() $G = \mathbb {Z}$
[Reference Boyle3, Reference Krieger13]. The marker patterns allow one to uniquely decode, from a given image point
$G = \mathbb {Z}$
[Reference Boyle3, Reference Krieger13]. The marker patterns allow one to uniquely decode, from a given image point
![]() $y = \psi (x)$
, which quasi-tiling
$y = \psi (x)$
, which quasi-tiling
![]() $t = {\mathcal T}(x)$
was used to construct y to begin with. Then, the tile pattern injections from earlier allow one to uniquely reconstruct the preimage x.
$t = {\mathcal T}(x)$
was used to construct y to begin with. Then, the tile pattern injections from earlier allow one to uniquely reconstruct the preimage x.
We note that the class of strongly aperiodic subshifts is well populated. It is known, for instance, that every countable group exhibits a strongly aperiodic subshift on the alphabet
![]() $\{0,1\}$
[Reference Aubrun, Barbieri and Thomassé1, Theorem 2.4]. Moreover, if
$\{0,1\}$
[Reference Aubrun, Barbieri and Thomassé1, Theorem 2.4]. Moreover, if
![]() $X_1$
is a strongly aperiodic subshift and
$X_1$
is a strongly aperiodic subshift and
![]() $X_2$
is an arbitrary subshift, then the direct product (Definition 2.13)
$X_2$
is an arbitrary subshift, then the direct product (Definition 2.13)
![]() $X_1 \times X_2$
is also strongly aperiodic; hence, there are at least as many strongly aperiodic subshifts as there are subshifts, in the sense of cardinality.
$X_1 \times X_2$
is also strongly aperiodic; hence, there are at least as many strongly aperiodic subshifts as there are subshifts, in the sense of cardinality.
We also mention here the similarity of hypotheses between the present work and contemporary work by Huczek and Kopacz [Reference Huczek and Kopacz11] that considers the ‘factor problem’ (under what hypotheses on X and Y does there exist a surjective homomorphism from X to Y?) for subshifts over discrete amenable groups, which is complementary to the embedding problem. In particular, [Reference Huczek and Kopacz11, Theorem 2.12] uses the comparison property of G in a form similar to Theorem 2.11. Additionally, [Reference Huczek and Kopacz11, Theorem 5.1] assumes that the domain X is strongly irreducible and that X exhibits, for each finite subset
![]() $F\subset G$
, a pattern that exhibits no element of F as a period. This latter condition is (under assumption of strong irreducibility) equivalent to our ‘separating elements’ condition (Definition 3.1), which is the form in which we appeal to the faithfulness of the shift action of G on Y.
$F\subset G$
, a pattern that exhibits no element of F as a period. This latter condition is (under assumption of strong irreducibility) equivalent to our ‘separating elements’ condition (Definition 3.1), which is the form in which we appeal to the faithfulness of the shift action of G on Y.
The paper is organized as follows. In §2, we review some preliminary material about countable amenable groups, symbolic dynamics, and quasi-tilings over countable amenable groups with and without the comparison property. In §3, we present our main results. We first construct a subsystem
![]() $Y_0 \subset Y$
that we pass to in the construction of our embedding (Theorem 3.2). We then construct marker patterns for Y (Theorem 3.4). Finally, we present the construction of our embedding of X into Y (Theorem 3.5). In §4, we discuss various ways in which Theorem 3.5 could potentially be strengthened and associated obstacles.
$Y_0 \subset Y$
that we pass to in the construction of our embedding (Theorem 3.2). We then construct marker patterns for Y (Theorem 3.4). Finally, we present the construction of our embedding of X into Y (Theorem 3.5). In §4, we discuss various ways in which Theorem 3.5 could potentially be strengthened and associated obstacles.
2. Preliminaries
2.1. Amenable groups
In this section, we briefly review the theory of countable amenable groups and state a few lemmas that shall be needed later. For a more thorough introduction to the theory of dynamics on amenable groups, see [Reference Kerr and Li12].
Definition 2.1. (Invariance, amenability, and Følner sequences)
Let G be a countable group, let
![]() $K \subset G$
be a finite subset, and let
$K \subset G$
be a finite subset, and let
![]() $\varepsilon> 0$
. A finite subset
$\varepsilon> 0$
. A finite subset
![]() $F \subset G$
is said to be
$F \subset G$
is said to be
![]() $(K,\varepsilon )$
-invariant if
$(K,\varepsilon )$
-invariant if
The group G is amenable if, for any finite subset
![]() $K \subset G$
and
$K \subset G$
and
![]() $\varepsilon> 0$
, there exists a finite subset
$\varepsilon> 0$
, there exists a finite subset
![]() $F \subset G$
that is
$F \subset G$
that is
![]() $(K,\varepsilon )$
-invariant. Equivalently, G is amenable if there exists a sequence
$(K,\varepsilon )$
-invariant. Equivalently, G is amenable if there exists a sequence
![]() $(F_n)_n$
of finite subsets of G such that for each fixed finite subset
$(F_n)_n$
of finite subsets of G such that for each fixed finite subset
![]() $K \subset G$
, it holds that
$K \subset G$
, it holds that
In this case, we say that
![]() $(F_n)_n$
is a (right) Følner sequence.
$(F_n)_n$
is a (right) Følner sequence.
Throughout this paper, G denotes a fixed countable amenable group with identity element e. It is classically known [Reference Namioka17, Theorem 5.2] that G exhibits a Følner sequence
![]() $(F_n)_n$
that is ascending (
$(F_n)_n$
that is ascending (
![]() $F_n \subset F_{n+1}$
for each n), that satisfies
$F_n \subset F_{n+1}$
for each n), that satisfies
![]() $\bigcup _n F_n = G$
, and such that each
$\bigcup _n F_n = G$
, and such that each
![]() $F_n$
is symmetric (
$F_n$
is symmetric (
![]() $F_n^{-1} = F_n$
). Throughout this paper,
$F_n^{-1} = F_n$
). Throughout this paper,
![]() $(F_n)_n$
denotes a fixed Følner sequence with all of the above properties. The symmetry property implies that
$(F_n)_n$
denotes a fixed Følner sequence with all of the above properties. The symmetry property implies that
![]() $(F_n)_n$
is both left Følner and right Følner, because for each finite subset
$(F_n)_n$
is both left Følner and right Følner, because for each finite subset
![]() $K \subset G$
, we have that
$K \subset G$
, we have that
In this setting, when a finite subset
![]() $F \subset G$
is described as ‘large’, it is implied that F is
$F \subset G$
is described as ‘large’, it is implied that F is
![]() $(K,\varepsilon )$
-invariant for some finite subset
$(K,\varepsilon )$
-invariant for some finite subset
![]() $K \subset G$
and
$K \subset G$
and
![]() $\varepsilon> 0$
, which may be clear from context or chosen arbitrarily beforehand. This sort of terminology is common but vague; a precise formulation is as follows. Let
$\varepsilon> 0$
, which may be clear from context or chosen arbitrarily beforehand. This sort of terminology is common but vague; a precise formulation is as follows. Let
![]() $\phi (F)$
be a property of finite subsets
$\phi (F)$
be a property of finite subsets
![]() $F\subset G$
. We shall say
$F\subset G$
. We shall say
![]() $\phi (F)$
holds for all sufficiently large F if there is a
$\phi (F)$
holds for all sufficiently large F if there is a
![]() $(K,\varepsilon )$
such that if F is
$(K,\varepsilon )$
such that if F is
![]() $(K,\varepsilon )$
-invariant, then
$(K,\varepsilon )$
-invariant, then
![]() $\phi (F)$
is true. We shall say
$\phi (F)$
is true. We shall say
![]() $\phi (F)$
holds for arbitrarily large subsets F if for every
$\phi (F)$
holds for arbitrarily large subsets F if for every
![]() $(K,\varepsilon )$
, there is a set F for which F is
$(K,\varepsilon )$
, there is a set F for which F is
![]() $(K,\varepsilon )$
-invariant and
$(K,\varepsilon )$
-invariant and
![]() $\phi (F)$
is true.
$\phi (F)$
is true.
We shall need the following elementary lemma; we omit the proof for brevity.
Lemma 2.1. Let
![]() $K \subset G$
be a finite subset with
$K \subset G$
be a finite subset with
![]() $e \in K$
. For any two finite subsets
$e \in K$
. For any two finite subsets
![]() $F_0$
,
$F_0$
,
![]() $F_1 \subset G$
, it holds that
$F_1 \subset G$
, it holds that
Next, we review concepts relating to the geometry of finite subsets of G.
Definition 2.2. (Boundary and interior)
Let
![]() $F \subset G$
and
$F \subset G$
and
![]() $K \subset G$
be finite subsets. The K-boundary of F is the subset
$K \subset G$
be finite subsets. The K-boundary of F is the subset
and the K-interior of F is the subset
Observe
![]() $F = \partial _K F \sqcup \operatorname {\mathrm {int}}_K F$
.
$F = \partial _K F \sqcup \operatorname {\mathrm {int}}_K F$
.
We shall need the following elementary lemmas; see [Reference Bland, McGoff and Pavlov2, Lemmas 2.1, 2.2].
Lemma 2.2. Let F,
![]() $K \subset G$
be finite subsets and let
$K \subset G$
be finite subsets and let
![]() $g\in G$
be arbitrary. If
$g\in G$
be arbitrary. If
![]() $Kg$
intersects
$Kg$
intersects
![]() $\operatorname {\mathrm {int}}_{KK^{-1}}F$
, then
$\operatorname {\mathrm {int}}_{KK^{-1}}F$
, then
![]() $Kg \subset F$
.
$Kg \subset F$
.
Lemma 2.3. Let F,
![]() $K \subset G$
be finite subsets. It holds that
$K \subset G$
be finite subsets. It holds that
Next we review the notion of density for infinite subsets of G. Roughly speaking, an infinite subset
![]() $C \subset G$
has density
$C \subset G$
has density
![]() $\rho \in [0,1]$
if, whenever a finite subset F is sufficiently large, it holds for all
$\rho \in [0,1]$
if, whenever a finite subset F is sufficiently large, it holds for all
![]() $g\in G$
that
$g\in G$
that
We use the Følner sequence to make this notion precise.
Definition 2.3. (Banach density)
Given a subset
![]() $C \subset G$
, the upper Banach density of C is
$C \subset G$
, the upper Banach density of C is
 $$ \begin{align*} \overline{D}(C) = \liminf_{n\to\infty} \sup_{g\in G}\frac{|F_n\cap Cg|}{|F_n|} \end{align*} $$
$$ \begin{align*} \overline{D}(C) = \liminf_{n\to\infty} \sup_{g\in G}\frac{|F_n\cap Cg|}{|F_n|} \end{align*} $$
and the lower Banach density of C is
These definitions have also appeared in the recent work on quasi-tilings of amenable groups due to Downarowicz, Huczek, and Zhang [Reference Downarowicz and Huczek6–Reference Downarowicz and Zhang9]. The value of the upper (respectively lower) density does not depend on the choice of Følner sequence [Reference Downarowicz, Huczek and Zhang7, Lemma 2.9]. Note that
![]() $\overline {D}(C) = 1- \underline {D}(G\setminus C)$
holds for any subset
$\overline {D}(C) = 1- \underline {D}(G\setminus C)$
holds for any subset
![]() $C\subset G$
.
$C\subset G$
.
Next we review a notion regarding how an infinite subset
![]() $C \subset G$
may be distributed throughout the group G.
$C \subset G$
may be distributed throughout the group G.
Definition 2.4. (Separation)
Given a finite subset
![]() $L \subset G$
, we say an infinite subset
$L \subset G$
, we say an infinite subset
![]() $C \subset G$
is L-separated if
$C \subset G$
is L-separated if
![]() $Lc_1 \cap Lc_2 = \varnothing $
for every distinct pair
$Lc_1 \cap Lc_2 = \varnothing $
for every distinct pair
![]() $c_1 \neq c_2 \in C$
.
$c_1 \neq c_2 \in C$
.
Note that if C is L-separated, then so is
![]() $Cg$
for each fixed
$Cg$
for each fixed
![]() $g\in G$
. Using this fact, one may easily check that if C is L-separated, then
$g\in G$
. Using this fact, one may easily check that if C is L-separated, then
![]() $\overline {D}(C) \leq 1/|L|$
. The following lemma states something slightly stronger.
$\overline {D}(C) \leq 1/|L|$
. The following lemma states something slightly stronger.
Lemma 2.4. Let M,
![]() $L\subset G$
be finite subsets with
$L\subset G$
be finite subsets with
![]() $e \in M \subset L$
. For any non-empty finite subset
$e \in M \subset L$
. For any non-empty finite subset
![]() $F \subset G$
and any L-separated subset
$F \subset G$
and any L-separated subset
![]() $C \subset G$
, we have that
$C \subset G$
, we have that
 $$ \begin{align*} \frac{|F\cap MC|}{|F|} \leq \frac{|M|}{|L|} + |M| \frac{|\partial_L F|}{|F|} + |M| \frac{|M^{-1}F\setminus F|}{|F|}. \end{align*} $$
$$ \begin{align*} \frac{|F\cap MC|}{|F|} \leq \frac{|M|}{|L|} + |M| \frac{|\partial_L F|}{|F|} + |M| \frac{|M^{-1}F\setminus F|}{|F|}. \end{align*} $$
Proof. Note that C is also M-separated by inclusion. Let
![]() $C^\times = \{c\in C : F\cap Mc \neq \varnothing \}$
. Observe that
$C^\times = \{c\in C : F\cap Mc \neq \varnothing \}$
. Observe that
![]() $C^{\times }$
is finite, as
$C^{\times }$
is finite, as
![]() $C^\times \subset M^{-1}F$
. By the fact that C is M-separated, we have
$C^\times \subset M^{-1}F$
. By the fact that C is M-separated, we have
Now let
![]() $C^\circ = \{c\in C : Lc\subset F\}$
. Observe that
$C^\circ = \{c\in C : Lc\subset F\}$
. Observe that
![]() $C^\circ \subset C^\times $
. We emphasize that
$C^\circ \subset C^\times $
. We emphasize that
![]() $C^\times $
is given in terms of M, while
$C^\times $
is given in terms of M, while
![]() $C^\circ $
is given in terms of L. By definition, we have
$C^\circ $
is given in terms of L. By definition, we have
![]() $LC^\circ \subset F$
, in which case
$LC^\circ \subset F$
, in which case
where the equality is a consequence of the fact that C is L-separated. Hence
![]() ${|C^\circ | \leq |F|/|L|}$
.
${|C^\circ | \leq |F|/|L|}$
.
Let
![]() $c \in C^\times \setminus C^\circ $
be fixed, in which case
$c \in C^\times \setminus C^\circ $
be fixed, in which case
![]() $F\cap Mc \neq \varnothing $
and
$F\cap Mc \neq \varnothing $
and
![]() $Lc \not \subset F$
. Therefore, if
$Lc \not \subset F$
. Therefore, if
![]() ${c\in F}$
, then
${c\in F}$
, then
![]() $c \in \partial _L F$
, while if
$c \in \partial _L F$
, while if
![]() $c \notin F$
, then
$c \notin F$
, then
![]() $c \in M^{-1}F\setminus F$
. This demonstrates that
$c \in M^{-1}F\setminus F$
. This demonstrates that
From this, we see that
 $$ \begin{align*} |F\cap MC| &\leq |M||C^\times|\\ &= |M||C^\circ| + |M||C^\times \setminus C^\circ|\\ &\leq |M|\frac{|F|}{|L|} + |M||\partial_L F| + |M| |M^{-1}F\setminus F|. \end{align*} $$
$$ \begin{align*} |F\cap MC| &\leq |M||C^\times|\\ &= |M||C^\circ| + |M||C^\times \setminus C^\circ|\\ &\leq |M|\frac{|F|}{|L|} + |M||\partial_L F| + |M| |M^{-1}F\setminus F|. \end{align*} $$
After dividing by
![]() $|F|$
, we obtain the conclusion.
$|F|$
, we obtain the conclusion.
With M and L fixed as in the above lemma, if one chooses
![]() $F = F_n$
and lets n approach infinity, then one may easily see that
$F = F_n$
and lets n approach infinity, then one may easily see that
![]() $\overline {D}(MC) \leq |M|/|L|$
whenever
$\overline {D}(MC) \leq |M|/|L|$
whenever
![]() $C\subset G$
is L-separated. However, what is especially significant for our purposes here is that the density of
$C\subset G$
is L-separated. However, what is especially significant for our purposes here is that the density of
![]() $MC$
can be estimated by sets F that are sufficiently large with respect to M and L alone, and there is no dependence on C other than the fact that C is L-separated. If C were an arbitrary subset satisfying
$MC$
can be estimated by sets F that are sufficiently large with respect to M and L alone, and there is no dependence on C other than the fact that C is L-separated. If C were an arbitrary subset satisfying
![]() $\overline {D}(C) < \varepsilon $
, then that density is not in general approximated by finite subsets except for very large ones, depending on C.
$\overline {D}(C) < \varepsilon $
, then that density is not in general approximated by finite subsets except for very large ones, depending on C.
2.2. Shifts and subshifts
In this section, we briefly review symbolic dynamics for amenable groups and state a few useful lemmas. For a more thorough introduction to symbolic dynamics and dynamics on amenable groups, see [Reference Kerr and Li12, Reference Lind and Marcus16].
Definition 2.5. (Labelings and patterns)
Let
![]() ${\mathcal A}$
be a finite alphabet of symbols, endowed with the discrete topology. A function
${\mathcal A}$
be a finite alphabet of symbols, endowed with the discrete topology. A function
![]() $x : G \to {\mathcal A}$
is an
$x : G \to {\mathcal A}$
is an
![]() ${\mathcal A}$
-labeling of G. The set of all such labelings is denoted
${\mathcal A}$
-labeling of G. The set of all such labelings is denoted
![]() ${\mathcal A}^G$
, which is endowed with the product topology. Given a finite subset
${\mathcal A}^G$
, which is endowed with the product topology. Given a finite subset
![]() $F \subset G$
, a function
$F \subset G$
, a function
![]() $p : F \to {\mathcal A}$
is called a pattern, said to be of shape F. The set of all patterns of shape F is denoted
$p : F \to {\mathcal A}$
is called a pattern, said to be of shape F. The set of all patterns of shape F is denoted
![]() ${\mathcal A}^F$
, and the set of all patterns of any shape is denoted
${\mathcal A}^F$
, and the set of all patterns of any shape is denoted
![]() ${\mathcal A}^{*}$
.
${\mathcal A}^{*}$
.
Given a point
![]() $x \in {\mathcal A}^G$
and a finite subset
$x \in {\mathcal A}^G$
and a finite subset
![]() $F \subset G$
, in this paper, we shall take
$F \subset G$
, in this paper, we shall take
![]() $x(F)$
to mean the restriction of x to F, which is itself a pattern of shape F. This is normally denoted
$x(F)$
to mean the restriction of x to F, which is itself a pattern of shape F. This is normally denoted
![]() $x|_F \in {\mathcal A}^F$
, but we raise the F from the subscript for readability. We shall also extend this notation to patterns where suitable; given a subset
$x|_F \in {\mathcal A}^F$
, but we raise the F from the subscript for readability. We shall also extend this notation to patterns where suitable; given a subset
![]() $F' \subset F$
and a pattern
$F' \subset F$
and a pattern
![]() $p \in {\mathcal A}^F$
, we shall take
$p \in {\mathcal A}^F$
, we shall take
![]() $p(F')$
to mean the restriction of p to
$p(F')$
to mean the restriction of p to
![]() $F'$
.
$F'$
.
Definition 2.6. (Shifts and subshifts)
The group G acts on
![]() ${\mathcal A}^G$
by way of (right) translations; for each fixed
${\mathcal A}^G$
by way of (right) translations; for each fixed
![]() $g \in G$
, we have a homeomorphism
$g \in G$
, we have a homeomorphism
![]() $\sigma ^g : {\mathcal A}^G \to {\mathcal A}^G$
given by
$\sigma ^g : {\mathcal A}^G \to {\mathcal A}^G$
given by
![]() $\sigma ^g(x)(g_1) = x(g_1g)$
for every
$\sigma ^g(x)(g_1) = x(g_1g)$
for every
![]() $g_1 \in G$
and
$g_1 \in G$
and
![]() $x \in X$
. The action
$x \in X$
. The action
![]() $\sigma = (\sigma ^g)_g$
is called the shift action of G on
$\sigma = (\sigma ^g)_g$
is called the shift action of G on
![]() ${\mathcal A}^G$
and, together,
${\mathcal A}^G$
and, together,
![]() $({\mathcal A}^G,\sigma )$
is a dynamical system called the full shift over
$({\mathcal A}^G,\sigma )$
is a dynamical system called the full shift over
![]() ${\mathcal A}$
. A subshift is a subset
${\mathcal A}$
. A subshift is a subset
![]() $X \subset {\mathcal A}^G$
that is
$X \subset {\mathcal A}^G$
that is
![]() $\sigma $
-invariant and closed in the topology of
$\sigma $
-invariant and closed in the topology of
![]() ${\mathcal A}^G$
.
${\mathcal A}^G$
.
A fixed point is a point
![]() $x\in {\mathcal A}^G$
such that
$x\in {\mathcal A}^G$
such that
![]() $x(g_1) = x(g_2)$
for every
$x(g_1) = x(g_2)$
for every
![]() $g_1$
,
$g_1$
,
![]() $g_2\in G$
, in which case
$g_2\in G$
, in which case
![]() $X = \{x\}$
is a trivial subshift. We shall say a subshift
$X = \{x\}$
is a trivial subshift. We shall say a subshift
![]() $X\subset {\mathcal A}^G$
is non-trivial if it contains at least two points. We shall also assume for each subshift
$X\subset {\mathcal A}^G$
is non-trivial if it contains at least two points. We shall also assume for each subshift
![]() $X \subset {\mathcal A}^G$
that the alphabet
$X \subset {\mathcal A}^G$
that the alphabet
![]() ${\mathcal A}$
is taken to be minimal, in the sense that every symbol
${\mathcal A}$
is taken to be minimal, in the sense that every symbol
![]() $a\in {\mathcal A}$
appears in at least one point
$a\in {\mathcal A}$
appears in at least one point
![]() $x\in X$
. Note that for a non-trivial subshift X, it necessarily holds that
$x\in X$
. Note that for a non-trivial subshift X, it necessarily holds that
![]() $|{\mathcal A}| \geq 2$
.
$|{\mathcal A}| \geq 2$
.
Definition 2.7. (Patterns in subshifts)
A pattern
![]() $p \in {\mathcal A}^F$
is said to appear in a point
$p \in {\mathcal A}^F$
is said to appear in a point
![]() ${x \in {\mathcal A}^G}$
at an element
${x \in {\mathcal A}^G}$
at an element
![]() $g \in G$
if
$g \in G$
if
![]() $\sigma ^g(x)(F) = p$
. The set of all patterns of shape F appearing in any point of X is denoted
$\sigma ^g(x)(F) = p$
. The set of all patterns of shape F appearing in any point of X is denoted
![]() ${\mathcal P}(F,X) \subset {\mathcal A}^F$
. The set of all patterns of any shape appearing in any point of X is denoted
${\mathcal P}(F,X) \subset {\mathcal A}^F$
. The set of all patterns of any shape appearing in any point of X is denoted
![]() ${\mathcal P}(X) \subset {\mathcal A}^{*}$
.
${\mathcal P}(X) \subset {\mathcal A}^{*}$
.
Given a subshift
![]() $X \subset {\mathcal A}^G$
and a (finite or infinite) collection of patterns
$X \subset {\mathcal A}^G$
and a (finite or infinite) collection of patterns
![]() ${\mathcal F} \subset {\mathcal A}^{*}$
, one may construct a subshift
${\mathcal F} \subset {\mathcal A}^{*}$
, one may construct a subshift
![]() $X_0 \subset X$
by expressly forbidding the patterns in
$X_0 \subset X$
by expressly forbidding the patterns in
![]() ${\mathcal F}$
from appearing in the points of X. That is,
${\mathcal F}$
from appearing in the points of X. That is,
We denote the subshift
![]() $X_0$
by
$X_0$
by
![]() $\langle X \mid {\mathcal F} \rangle $
. Every subshift may be realized in this form; indeed,
$\langle X \mid {\mathcal F} \rangle $
. Every subshift may be realized in this form; indeed,
![]() $X = \langle {\mathcal A}^G \mid {\mathcal A}^{*} \setminus {\mathcal P}(X)\rangle $
holds for every subshift
$X = \langle {\mathcal A}^G \mid {\mathcal A}^{*} \setminus {\mathcal P}(X)\rangle $
holds for every subshift
![]() $X \subset {\mathcal A}^G$
.
$X \subset {\mathcal A}^G$
.
Next we review some special classes of subshifts.
Definition 2.8. (Strongly aperiodic subshifts)
A point x is aperiodic if
![]() $\sigma ^g(x) = x$
only when
$\sigma ^g(x) = x$
only when
![]() $g = e$
. A subshift X is strongly aperiodic if every
$g = e$
. A subshift X is strongly aperiodic if every
![]() $x \in X$
is aperiodic. In other words, the action
$x \in X$
is aperiodic. In other words, the action
![]() $\sigma $
is free on X.
$\sigma $
is free on X.
Definition 2.9. (Shifts of finite type)
A subshift
![]() $Y \subset {\mathcal A}^G$
is a shift of finite type (SFT) if there exists a finite collection of patterns
$Y \subset {\mathcal A}^G$
is a shift of finite type (SFT) if there exists a finite collection of patterns
![]() ${\mathcal F} \subset {\mathcal A}^{*}$
such that
${\mathcal F} \subset {\mathcal A}^{*}$
such that
![]() $Y = \langle {\mathcal A}^G \mid {\mathcal F} \rangle $
. For such a subshift, it is always possible to take
$Y = \langle {\mathcal A}^G \mid {\mathcal F} \rangle $
. For such a subshift, it is always possible to take
![]() ${\mathcal F}$
in the form
${\mathcal F}$
in the form
![]() ${\mathcal A}^K \setminus {\mathcal P}(K,Y)$
for some finite subset
${\mathcal A}^K \setminus {\mathcal P}(K,Y)$
for some finite subset
![]() $K \subset G$
. In this case, we say that K witnesses Y as an SFT.
$K \subset G$
. In this case, we say that K witnesses Y as an SFT.
We will need the following elementary lemma; see [Reference Bland, McGoff and Pavlov2, Lemma 2.8].
Lemma 2.5. Let Y be an SFT witnessed by
![]() $K \subset G$
, let
$K \subset G$
, let
![]() $y_1$
,
$y_1$
,
![]() $y_2 \in Y$
be arbitrary points, and let
$y_2 \in Y$
be arbitrary points, and let
![]() $F\subset G$
be a finite subset. If
$F\subset G$
be a finite subset. If
![]() $y_1(\partial _{KK^{-1}}F) = y_2(\partial _{KK^{-1}}F)$
, then the point y given by
$y_1(\partial _{KK^{-1}}F) = y_2(\partial _{KK^{-1}}F)$
, then the point y given by
![]() $y(g) = y_1(g)$
if
$y(g) = y_1(g)$
if
![]() $g \in F$
and
$g \in F$
and
![]() $y(g) = y_2(g)$
if
$y(g) = y_2(g)$
if
![]() $g\in G\setminus F$
is a point belonging to Y.
$g\in G\setminus F$
is a point belonging to Y.
Definition 2.10. (Strong irreducibility)
A subshift
![]() $Y \subset {\mathcal A}^G$
is strongly irreducible if there exists a finite subset
$Y \subset {\mathcal A}^G$
is strongly irreducible if there exists a finite subset
![]() $K \subset G$
with
$K \subset G$
with
![]() $e\in K$
such that for any finite subsets
$e\in K$
such that for any finite subsets
![]() $F_1$
,
$F_1$
,
![]() $F_2 \subset G$
and allowed patterns
$F_2 \subset G$
and allowed patterns
![]() $p_1 \in {\mathcal P}(F_1, Y)$
and
$p_1 \in {\mathcal P}(F_1, Y)$
and
![]() $p_2 \in {\mathcal P}(F_2, Y)$
, if
$p_2 \in {\mathcal P}(F_2, Y)$
, if
![]() $KF_1$
is disjoint from
$KF_1$
is disjoint from
![]() $F_2$
, then there is a point
$F_2$
, then there is a point
![]() $y \in Y$
such that
$y \in Y$
such that
![]() $y(F_1) = p_1$
and
$y(F_1) = p_1$
and
![]() $y(F_2) = p_2$
. In this case, we say that K witnesses Y as strongly irreducible or that Y is a strongly irreducible subshift of parameter K.
$y(F_2) = p_2$
. In this case, we say that K witnesses Y as strongly irreducible or that Y is a strongly irreducible subshift of parameter K.
Note that strong irreducibility is preserved under taking factors (Definition 2.12) and products (Definition 2.13) of subshifts. Strong irreducibility is equivalent to a seemingly stronger mixing condition, as the following lemma demonstrates. The proof relies on a standard compactness argument; we omit it for brevity.
Lemma 2.6. Suppose Y is a strongly irreducible subshift of parameter
![]() $K \subset G$
. For any finite subset
$K \subset G$
. For any finite subset
![]() $F \subset G$
and points
$F \subset G$
and points
![]() $y_1$
,
$y_1$
,
![]() $y_2 \in Y$
, there is a point
$y_2 \in Y$
, there is a point
![]() $y \in Y$
such that
$y \in Y$
such that
Next we review topological entropy of subshifts.
Definition 2.11. (Entropy)
The (topological) entropy of a subshift X is given by
where
![]() $h(F, X) = ({1}/{|F|}) \log \!|{\mathcal P}(F, X)|$
for each non-empty finite subset
$h(F, X) = ({1}/{|F|}) \log \!|{\mathcal P}(F, X)|$
for each non-empty finite subset
![]() $F\subset G$
and
$F\subset G$
and
![]() $(F_n)_n$
is a Følner sequence for G.
$(F_n)_n$
is a Følner sequence for G.
It is classically known [Reference Kerr and Li12, Theorem 4.38] that the limit above exists and does not depend on the choice of Følner sequence. Indeed, more recently, it has been shown that
where the infimum is taken over all finite subsets
![]() $F \subset G$
[Reference Downarowicz, Frej and Romagnoli5, Corollary 6.3].
$F \subset G$
[Reference Downarowicz, Frej and Romagnoli5, Corollary 6.3].
Next we review homomorphisms between subshifts.
Definition 2.12. (Homomorphisms)
Let
![]() ${\mathcal A}_X$
and
${\mathcal A}_X$
and
![]() ${\mathcal A}_Y$
be finite alphabets, and let
${\mathcal A}_Y$
be finite alphabets, and let
![]() $X \subset {\mathcal A}_X^G$
and
$X \subset {\mathcal A}_X^G$
and
![]() $Y \subset {\mathcal A}_Y^G$
be subshifts. A homomorphism between X and Y is a map
$Y \subset {\mathcal A}_Y^G$
be subshifts. A homomorphism between X and Y is a map
![]() $\phi : X \to Y$
that is both continuous and shift-commuting. By the Curtis–Lyndon–Hedlund theorem [Reference Ceccherini-Silberstein and Coornaert4, Theorem 1.8.1], a map
$\phi : X \to Y$
that is both continuous and shift-commuting. By the Curtis–Lyndon–Hedlund theorem [Reference Ceccherini-Silberstein and Coornaert4, Theorem 1.8.1], a map
![]() $\phi : X \to Y$
is a homomorphism if and only if there exists a finite subset
$\phi : X \to Y$
is a homomorphism if and only if there exists a finite subset
![]() $F \subset G$
and a function
$F \subset G$
and a function
![]() $\Phi : {\mathcal P}(F,X) \to {\mathcal A}_Y$
such that for every
$\Phi : {\mathcal P}(F,X) \to {\mathcal A}_Y$
such that for every
![]() $g\in G$
and
$g\in G$
and
![]() $x\in X$
, it holds that
$x\in X$
, it holds that
If
![]() $\phi $
is surjective, then
$\phi $
is surjective, then
![]() $\phi $
is said to be a factor map, X is said to factor onto Y, and Y is said to be a factor of X. If
$\phi $
is said to be a factor map, X is said to factor onto Y, and Y is said to be a factor of X. If
![]() $\phi $
is injective, then
$\phi $
is injective, then
![]() $\phi $
is said to be an embedding and X is said to embed into Y.
$\phi $
is said to be an embedding and X is said to embed into Y.
If X embeds into Y, then
![]() $h(X) \leq h(Y)$
. If X factors onto Y, then
$h(X) \leq h(Y)$
. If X factors onto Y, then
![]() $h(X) \geq h(Y)$
.
$h(X) \geq h(Y)$
.
Next we review the primary way by which we join two subshifts together.
Definition 2.13. (Product systems)
Let
![]() ${\mathcal A}$
and
${\mathcal A}$
and
![]() $\Lambda $
be finite alphabets and let
$\Lambda $
be finite alphabets and let
![]() $X \subset {\mathcal A}^G$
and
$X \subset {\mathcal A}^G$
and
![]() $T \subset \Lambda ^G$
be subshifts. The product system
$T \subset \Lambda ^G$
be subshifts. The product system
![]() $X \times T$
equipped with the action
$X \times T$
equipped with the action
![]() $\varsigma $
given by
$\varsigma $
given by
![]() $\varsigma ^g(x,t) = (\sigma ^g(x), \sigma ^g(t))$
is isomorphic to a subshift over the alphabet
$\varsigma ^g(x,t) = (\sigma ^g(x), \sigma ^g(t))$
is isomorphic to a subshift over the alphabet
![]() ${\mathcal A} \times \Lambda $
, with
${\mathcal A} \times \Lambda $
, with
![]() $(x,t)$
corresponding to the point
$(x,t)$
corresponding to the point
![]() $\tilde {x}$
such that
$\tilde {x}$
such that
![]() $\tilde {x}(g) = (x(g),t(g))$
for each
$\tilde {x}(g) = (x(g),t(g))$
for each
![]() $g\in G$
. Abusing notation, we regard
$g\in G$
. Abusing notation, we regard
![]() $X\times T$
as a subshift of
$X\times T$
as a subshift of
![]() $({\mathcal A}\times \Lambda )^G$
.
$({\mathcal A}\times \Lambda )^G$
.
The following lemma is a consequence of the fact that for a finite subset
![]() $F\subset G$
and subshifts X and T,
$F\subset G$
and subshifts X and T,
![]() $|{\mathcal P}(F, X\times T)| = |{\mathcal P}(F,X)|\cdot |{\mathcal P}(F,T)|$
.
$|{\mathcal P}(F, X\times T)| = |{\mathcal P}(F,X)|\cdot |{\mathcal P}(F,T)|$
.
Lemma 2.7. Let X and T be subshifts. Then
![]() $h(X \times T) = h(X) + h(T)$
.
$h(X \times T) = h(X) + h(T)$
.
2.3. Quasi-tilings
In this section, we review quasi-tilings of amenable groups, which were originally introduced and studied by Ornstein and Weiss [Reference Ornstein and Weiss18]. We also state a theorem of Downarowicz and Huczek that is essential for our main result.
Definition 2.14. (Quasi-tilings)
Let
![]() ${\mathcal S} = \{S_1, \ldots , S_r\}$
be a collection of finite, non-empty subsets of G which is ‘shift-irreducible’ in the sense that there is no pair of distinct subsets
${\mathcal S} = \{S_1, \ldots , S_r\}$
be a collection of finite, non-empty subsets of G which is ‘shift-irreducible’ in the sense that there is no pair of distinct subsets
![]() $S_1$
,
$S_1$
,
![]() $S_2 \in {\mathcal S}$
and element
$S_2 \in {\mathcal S}$
and element
![]() $g\in G$
for which
$g\in G$
for which
![]() $S_1 g = S_2$
. We refer to these subsets as shapes. A quasi-tiling of G over
$S_1 g = S_2$
. We refer to these subsets as shapes. A quasi-tiling of G over
![]() ${\mathcal S}$
is an assignment of each shape
${\mathcal S}$
is an assignment of each shape
![]() $S\in {\mathcal S}$
to a (generally infinite) subset
$S\in {\mathcal S}$
to a (generally infinite) subset
![]() $C_S \subset G$
(called the set of centers for S) such that the sets
$C_S \subset G$
(called the set of centers for S) such that the sets
![]() $\{C_S : S\in {\mathcal S}\}$
are pairwise disjoint and the map
$\{C_S : S\in {\mathcal S}\}$
are pairwise disjoint and the map
![]() $(S,c) \mapsto Sc$
is injective over
$(S,c) \mapsto Sc$
is injective over
![]() $\{(S,c) : S\in {\mathcal S} \text { and } c\in C_S\}$
.
$\{(S,c) : S\in {\mathcal S} \text { and } c\in C_S\}$
.
A quasi-tiling of G over
![]() ${\mathcal S}$
may be encoded as a point of the symbolic space
${\mathcal S}$
may be encoded as a point of the symbolic space
![]() $\Lambda ({\mathcal S})^G$
, where
$\Lambda ({\mathcal S})^G$
, where
![]() $\Lambda ({\mathcal S}) = {\mathcal S} \cup \{\varnothing \}$
is thought of as an alphabet of
$\Lambda ({\mathcal S}) = {\mathcal S} \cup \{\varnothing \}$
is thought of as an alphabet of
![]() $r + 1$
symbols. A point
$r + 1$
symbols. A point
![]() $t \in \Lambda ({\mathcal S})^G$
encodes the quasi-tiling when
$t \in \Lambda ({\mathcal S})^G$
encodes the quasi-tiling when
![]() $t(c) = S$
if and only if
$t(c) = S$
if and only if
![]() $c\in C_S$
for each
$c\in C_S$
for each
![]() $S\in {\mathcal S}$
and
$S\in {\mathcal S}$
and
![]() $c\in G$
, and
$c\in G$
, and
![]() $t(g) = \varnothing $
otherwise. Here we shall identify t with the quasi-tiling it formally encodes. We shall write
$t(g) = \varnothing $
otherwise. Here we shall identify t with the quasi-tiling it formally encodes. We shall write
![]() $C(t) = \{g\in G : t(g) \neq \varnothing \}$
, which is precisely the set
$C(t) = \{g\in G : t(g) \neq \varnothing \}$
, which is precisely the set
![]() $\bigcup _{S\in {\mathcal S}} C_S$
. A tile of a quasi-tiling t is a subset of G of the form
$\bigcup _{S\in {\mathcal S}} C_S$
. A tile of a quasi-tiling t is a subset of G of the form
![]() $t(c)c$
where
$t(c)c$
where
![]() $c\in C(t)$
. A system of quasi-tilings is a subshift
$c\in C(t)$
. A system of quasi-tilings is a subshift
![]() $T \subset \Lambda ({\mathcal S})^G$
such that every
$T \subset \Lambda ({\mathcal S})^G$
such that every
![]() $t\in T$
encodes a quasi-tiling of G over
$t\in T$
encodes a quasi-tiling of G over
![]() ${\mathcal S}$
.
${\mathcal S}$
.
A quasi-tiling t is disjoint if
![]() $t(g_1)g_1 \cap t(g_2)g_2 = \varnothing $
for every
$t(g_1)g_1 \cap t(g_2)g_2 = \varnothing $
for every
![]() $g_1 \neq g_2 \in G$
. A quasi-tiling t is said to cover the group G if
$g_1 \neq g_2 \in G$
. A quasi-tiling t is said to cover the group G if
![]() $\bigcup _{g} t(g)g = G$
. An exact tiling is one which is both disjoint and covers G (in other words, the tiles of t form a partition of G). For most applications, it is not necessary that quasi-tilings be exactly disjoint or exactly covering; it is often sufficient to have a quasi-tiling whose tiles are ‘nearly disjoint’ and which ‘nearly covers’ G. The following definition formalizes the ‘nearly disjoint’ condition.
$\bigcup _{g} t(g)g = G$
. An exact tiling is one which is both disjoint and covers G (in other words, the tiles of t form a partition of G). For most applications, it is not necessary that quasi-tilings be exactly disjoint or exactly covering; it is often sufficient to have a quasi-tiling whose tiles are ‘nearly disjoint’ and which ‘nearly covers’ G. The following definition formalizes the ‘nearly disjoint’ condition.
Definition 2.15. (Retractions and
 $\varepsilon $
-disjointness)
$\varepsilon $
-disjointness)
Given a quasi-tiling t, a retraction of t is any quasi-tiling
![]() $\operatorname {\mathrm {ret}}(t)$
(which is in general given over a different collection of shapes than t) such that
$\operatorname {\mathrm {ret}}(t)$
(which is in general given over a different collection of shapes than t) such that
![]() $\operatorname {\mathrm {ret}}(t)(g) \subset t(g)$
for every
$\operatorname {\mathrm {ret}}(t)(g) \subset t(g)$
for every
![]() $g \in G$
. Given
$g \in G$
. Given
![]() $\varepsilon> 0$
, a quasi-tiling t is said to be
$\varepsilon> 0$
, a quasi-tiling t is said to be
![]() $\varepsilon $
-disjoint if it has a disjoint retraction
$\varepsilon $
-disjoint if it has a disjoint retraction
![]() $\operatorname {\mathrm {ret}}(t)$
such that, for every
$\operatorname {\mathrm {ret}}(t)$
such that, for every
![]() $c\in C(t)$
, it holds that
$c\in C(t)$
, it holds that
In words, every tile of t may be ‘retracted’ to a subset of proportion at least
![]() $1-\varepsilon $
such that the retracted subsets are all pairwise disjoint.
$1-\varepsilon $
such that the retracted subsets are all pairwise disjoint.
The following definition formalizes the ‘nearly covering’ condition.
Definition 2.16. (
 $\rho $
-covering)
$\rho $
-covering)
Given
![]() $\rho \in (0,1)$
, a quasi-tiling t is
$\rho \in (0,1)$
, a quasi-tiling t is
![]() $\rho $
-covering if
$\rho $
-covering if
 $$ \begin{align*} \underline{D}\bigg(\bigcup_{g\in G}t(g)g\bigg) \geq \rho, \end{align*} $$
$$ \begin{align*} \underline{D}\bigg(\bigcup_{g\in G}t(g)g\bigg) \geq \rho, \end{align*} $$
where
![]() $\underline {D}$
is the lower Banach density (Definition 2.3).
$\underline {D}$
is the lower Banach density (Definition 2.3).
We shall need the following elementary lemma; see [Reference Downarowicz, Huczek and Zhang7, Lemma 3.4].
Lemma 2.8. Let
![]() $\rho _0$
,
$\rho _0$
,
![]() $\rho _1 \in (0,1)$
be fixed. Suppose
$\rho _1 \in (0,1)$
be fixed. Suppose
![]() $t_0$
is a
$t_0$
is a
![]() $\rho _0$
-covering quasi-tiling and suppose
$\rho _0$
-covering quasi-tiling and suppose
![]() $t_1$
is a disjoint retraction of
$t_1$
is a disjoint retraction of
![]() $t_0$
such that
$t_0$
such that
![]() $|t_1(c)| \geq \rho _1|t_0(c)|$
for each
$|t_1(c)| \geq \rho _1|t_0(c)|$
for each
![]() $c\in C(t_0)$
. Then
$c\in C(t_0)$
. Then
![]() $t_1$
is
$t_1$
is
![]() $\rho _0\rho _1$
-covering.
$\rho _0\rho _1$
-covering.
The existence of useful quasi-tilings over countable amenable groups (that is, with arbitrarily large shapes and arbitrarily good near-disjointness and near-covering properties) has been known in some form since 1987, due first to Ornstein and Weiss [Reference Ornstein and Weiss18, I.§2, Theorem 6]. This construction was sharpened in 2015 by Downarowicz, Huczek, and Zhang who demonstrated that a countable amenable group exhibits an exact tiling with arbitrarily large shapes; moreover, one can find a system of such tilings that has topological entropy zero [Reference Downarowicz, Huczek and Zhang7, Theorem 5.2].
For our purposes, we require not just that a system of nice quasi-tilings exists, but also that one may be obtained as a topological factor of a given subshift X. We have the following theorem of Downarowicz and Huczek [Reference Downarowicz and Huczek6, Lemma 3.4]. Not every property claimed here was stated in their theorem (here we state property (5) and the fact that the map
![]() $t\mapsto \operatorname {\mathrm {ret}}(t)$
in property (4) is a homomorphism), but a close reading of their proof reveals that it may be minorly modified to conclude this slightly stronger result. Here we provide a short argument that fills in the gaps, appealing to the construction in [Reference Downarowicz and Huczek6] as required.
$t\mapsto \operatorname {\mathrm {ret}}(t)$
in property (4) is a homomorphism), but a close reading of their proof reveals that it may be minorly modified to conclude this slightly stronger result. Here we provide a short argument that fills in the gaps, appealing to the construction in [Reference Downarowicz and Huczek6] as required.
Theorem 2.9. Let X be a strongly aperiodic subshift, let
![]() $\varepsilon \in (0,1/3)$
be arbitrary, and suppose that
$\varepsilon \in (0,1/3)$
be arbitrary, and suppose that
![]() $r \in \mathbb {N}$
satisfies
$r \in \mathbb {N}$
satisfies
![]() $(1-\varepsilon /2)^r < \varepsilon $
. For any
$(1-\varepsilon /2)^r < \varepsilon $
. For any
![]() $n_0 \in \mathbb {N}$
and finite subset
$n_0 \in \mathbb {N}$
and finite subset
![]() $L \subset G$
, there is a collection of shapes
$L \subset G$
, there is a collection of shapes
![]() ${\mathcal S} = \{F_{n_1}, \ldots , F_{n_r}\}$
and a system of quasi-tilings
${\mathcal S} = \{F_{n_1}, \ldots , F_{n_r}\}$
and a system of quasi-tilings
![]() $T \subset \Lambda ({\mathcal S})^G$
such that:
$T \subset \Lambda ({\mathcal S})^G$
such that:
-
(1)
 $n_0 < n_1 < \cdots < n_r$
;
$n_0 < n_1 < \cdots < n_r$
; -
(2) there is a factor map
 ${\mathcal T} : X \to T$
;
${\mathcal T} : X \to T$
; -
(3) every
 $t \in T$
is
$t \in T$
is
 $(1-\varepsilon )$
-covering;
$(1-\varepsilon )$
-covering; -
(4) every
 $t \in T$
is
$t \in T$
is
 $\varepsilon $
-disjoint as witnessed by a continuous and shift-commuting retraction map
$\varepsilon $
-disjoint as witnessed by a continuous and shift-commuting retraction map
 $t\mapsto \operatorname {\mathrm {ret}}(t)$
; and
$t\mapsto \operatorname {\mathrm {ret}}(t)$
; and -
(5) for every
 $t \in T$
, the set
$t \in T$
, the set
 $C(t)$
is L-separated.
$C(t)$
is L-separated.
Proof. In [Reference Downarowicz and Huczek6],
![]() $n_1$
is chosen as
$n_1$
is chosen as
![]() $n_0 + 1$
and
$n_0 + 1$
and
![]() $n_i$
is inductively chosen so that
$n_i$
is inductively chosen so that
![]() $F_{n_i}$
is
$F_{n_i}$
is
![]() $(F_{n_j}, \delta _j)$
-invariant for every
$(F_{n_j}, \delta _j)$
-invariant for every
![]() $j < i$
, where
$j < i$
, where
![]() $\delta _j> 0$
is specified in the construction. From this, we infer that
$\delta _j> 0$
is specified in the construction. From this, we infer that
![]() $n_i - n_{i-1}$
may be arbitrarily large for each
$n_i - n_{i-1}$
may be arbitrarily large for each
![]() $i = 1, \ldots , r$
. We therefore additionally assume that for each
$i = 1, \ldots , r$
. We therefore additionally assume that for each
![]() $i = 1, \ldots , r$
, we have the following properties.
$i = 1, \ldots , r$
, we have the following properties.
-
(P1)
 $|F_{n_i} \cap F_{n_i}\ell | \geq (1-\varepsilon )|F_{n_i}|$
for every
$|F_{n_i} \cap F_{n_i}\ell | \geq (1-\varepsilon )|F_{n_i}|$
for every
 $\ell \in L^{-1}L$
.
$\ell \in L^{-1}L$
. -
(P2)
 $F_{n_{i-1}} L^{-1} L \subset F_{n_i}$
.
$F_{n_{i-1}} L^{-1} L \subset F_{n_i}$
.
This is possible because the sequence
![]() $(F_n)_n$
was chosen to be both left and right Følner, to be ascending in n, and to satisfy
$(F_n)_n$
was chosen to be both left and right Følner, to be ascending in n, and to satisfy
![]() $\bigcup _n F_n = G$
(Definition 2.1).
$\bigcup _n F_n = G$
(Definition 2.1).
Let
![]() $S_i = F_{n_i}$
for each
$S_i = F_{n_i}$
for each
![]() $i = 1, \ldots , r$
and let
$i = 1, \ldots , r$
and let
![]() ${\mathcal S} = \{S_1, \ldots , S_r\}$
. Our modifications to the choice of
${\mathcal S} = \{S_1, \ldots , S_r\}$
. Our modifications to the choice of
![]() ${\mathcal S}$
preserve the invariance conditions assumed by [Reference Downarowicz and Huczek6]. We now define and construct everything else as in [Reference Downarowicz and Huczek6], summarized below.
${\mathcal S}$
preserve the invariance conditions assumed by [Reference Downarowicz and Huczek6]. We now define and construct everything else as in [Reference Downarowicz and Huczek6], summarized below.
Let
![]() $x \in X$
be fixed. In [Reference Downarowicz and Huczek6], the quasi-tiling
$x \in X$
be fixed. In [Reference Downarowicz and Huczek6], the quasi-tiling
![]() $t = {\mathcal T}(x) \in \Lambda ({\mathcal S})^G$
is constructed inductively, with the tiles of shape
$t = {\mathcal T}(x) \in \Lambda ({\mathcal S})^G$
is constructed inductively, with the tiles of shape
![]() $S_r$
chosen first, then
$S_r$
chosen first, then
![]() $S_{r-1}$
, and so on, down to
$S_{r-1}$
, and so on, down to
![]() $S_1$
. Consequently, for each
$S_1$
. Consequently, for each
![]() $c\in C(t)$
, there is a well-defined subset
$c\in C(t)$
, there is a well-defined subset
![]() $C(t)_{<c} \subset C(t)$
that denotes the centers of all the tiles laid before the tile at c in the inductive process. Some tiles of the same shape are laid simultaneously, so the implied ordering given by
$C(t)_{<c} \subset C(t)$
that denotes the centers of all the tiles laid before the tile at c in the inductive process. Some tiles of the same shape are laid simultaneously, so the implied ordering given by
![]() $c_1 < c_2$
if
$c_1 < c_2$
if
![]() $c_1 \in C(t)_{<c_2}$
is not total. However, tiles laid simultaneously in the construction of [Reference Downarowicz and Huczek6] are necessarily disjoint.
$c_1 \in C(t)_{<c_2}$
is not total. However, tiles laid simultaneously in the construction of [Reference Downarowicz and Huczek6] are necessarily disjoint.
This in hand, the retraction map
![]() $t\mapsto \operatorname {\mathrm {ret}}(t)$
is given by
$t\mapsto \operatorname {\mathrm {ret}}(t)$
is given by
 $$ \begin{align*} \operatorname{\mathrm{ret}}(t)(c) = t(c) \setminus \bigg( \bigcup_{c_0 \in C(t)_{<c}} t(c_0)c_0\bigg)c^{-1} \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{ret}}(t)(c) = t(c) \setminus \bigg( \bigcup_{c_0 \in C(t)_{<c}} t(c_0)c_0\bigg)c^{-1} \end{align*} $$
for each
![]() $c \in C(t)$
, and
$c \in C(t)$
, and
![]() $\operatorname {\mathrm {ret}}(t)(g) = \varnothing $
otherwise. In [Reference Downarowicz and Huczek6], it is shown by induction that this is a disjoint retraction satisfying
$\operatorname {\mathrm {ret}}(t)(g) = \varnothing $
otherwise. In [Reference Downarowicz and Huczek6], it is shown by induction that this is a disjoint retraction satisfying
![]() $|t(c)\setminus \operatorname {\mathrm {ret}}(t)(c)| < \varepsilon |t(c)|$
for each
$|t(c)\setminus \operatorname {\mathrm {ret}}(t)(c)| < \varepsilon |t(c)|$
for each
![]() $c\in C(t)$
. Moreover, it is quick to check that the map
$c\in C(t)$
. Moreover, it is quick to check that the map
![]() $t\mapsto \operatorname {\mathrm {ret}}(t)$
is continuous and shift-commuting, as the elements
$t\mapsto \operatorname {\mathrm {ret}}(t)$
is continuous and shift-commuting, as the elements
![]() $c_0 \in C(t)_{<c}$
with
$c_0 \in C(t)_{<c}$
with
![]() $t(c)c \cap t(c_0)c_0 \neq \varnothing $
are determined by
$t(c)c \cap t(c_0)c_0 \neq \varnothing $
are determined by
![]() $\sigma ^c(t)(F)$
for some (possibly very large) finite subset
$\sigma ^c(t)(F)$
for some (possibly very large) finite subset
![]() $F \subset G$
. The construction in [Reference Downarowicz and Huczek6] also gives that t is
$F \subset G$
. The construction in [Reference Downarowicz and Huczek6] also gives that t is
![]() $(1-\varepsilon )$
-covering.
$(1-\varepsilon )$
-covering.
Let
![]() $T = {\mathcal T}(X) \subset \Lambda ({\mathcal S})^G$
. From the observations of the previous paragraph, we see that properties (1) through (4) hold. For the theorem, it remains to check property (5): that
$T = {\mathcal T}(X) \subset \Lambda ({\mathcal S})^G$
. From the observations of the previous paragraph, we see that properties (1) through (4) hold. For the theorem, it remains to check property (5): that
![]() $C(t)$
is L-separated for each
$C(t)$
is L-separated for each
![]() $t \in T$
. Let
$t \in T$
. Let
![]() $t \in T$
be fixed and suppose in contrast that
$t \in T$
be fixed and suppose in contrast that
![]() ${Lc_1 \cap Lc_2 \neq \varnothing} $
for some distinct
${Lc_1 \cap Lc_2 \neq \varnothing} $
for some distinct
![]() $c_1 \neq c_2 \in C(t)$
, in which case
$c_1 \neq c_2 \in C(t)$
, in which case
![]() $c_1c_2^{-1} \in L^{-1}L$
. Let
$c_1c_2^{-1} \in L^{-1}L$
. Let
![]() $t(c_1) = S_i$
and
$t(c_1) = S_i$
and
![]() $t(c_2) = S_j$
and suppose without loss of generality that
$t(c_2) = S_j$
and suppose without loss of generality that
![]() $i \leq j$
.
$i \leq j$
.
If
![]() $i = j$
, then let
$i = j$
, then let
![]() $S = S_i = S_j$
, in which case
$S = S_i = S_j$
, in which case
![]() $|Sc_1 \cap Sc_2| = |S\cap Sc_1c_2^{-1}| \geq (1-\varepsilon )|S|$
by the assumed property (P1). Note that
$|Sc_1 \cap Sc_2| = |S\cap Sc_1c_2^{-1}| \geq (1-\varepsilon )|S|$
by the assumed property (P1). Note that
![]() $R_1 = \operatorname {\mathrm {ret}}(t)(c_1) \subset S$
and
$R_1 = \operatorname {\mathrm {ret}}(t)(c_1) \subset S$
and
![]() $R_2 = \operatorname {\mathrm {ret}}(t)(c_2) \subset S$
are subsets such that
$R_2 = \operatorname {\mathrm {ret}}(t)(c_2) \subset S$
are subsets such that
![]() $|S \setminus R_1| < \varepsilon |S|$
and
$|S \setminus R_1| < \varepsilon |S|$
and
![]() $|S \setminus R_2| < \varepsilon |S|$
by construction. Moreover, by construction,
$|S \setminus R_2| < \varepsilon |S|$
by construction. Moreover, by construction,
![]() $R_1c_1 \cap R_2c_2 = \varnothing $
, in which case
$R_1c_1 \cap R_2c_2 = \varnothing $
, in which case
![]() $Sc_1 \cap Sc_2 \subset (Sc_1 \setminus R_1 c_1) \cup (Sc_2 \setminus R_2 c_2)$
. This implies that
$Sc_1 \cap Sc_2 \subset (Sc_1 \setminus R_1 c_1) \cup (Sc_2 \setminus R_2 c_2)$
. This implies that
We thus obtain
![]() $(1-\varepsilon )|S| \leq |Sc_1\cap Sc_2| < 2\varepsilon |S|$
, which contradicts the assumption that
$(1-\varepsilon )|S| \leq |Sc_1\cap Sc_2| < 2\varepsilon |S|$
, which contradicts the assumption that
![]() $\varepsilon < 1/3$
.
$\varepsilon < 1/3$
.
In the second case, suppose
![]() $i < j$
. Then,
$i < j$
. Then,
![]() $c_1 c_2^{-1} \in L^{-1} L$
implies that
$c_1 c_2^{-1} \in L^{-1} L$
implies that
![]() ${S_ic_1c_2^{-1} \subset S_iL^{-1}L \subset S_j}$
by the assumed property (P2). Hence,
${S_ic_1c_2^{-1} \subset S_iL^{-1}L \subset S_j}$
by the assumed property (P2). Hence,
![]() $t(c_1)c_1 \subset t(c_2)c_2$
. This does not immediately contradict the
$t(c_1)c_1 \subset t(c_2)c_2$
. This does not immediately contradict the
![]() $\varepsilon $
-disjointness of t, as it may be the case that
$\varepsilon $
-disjointness of t, as it may be the case that
![]() $t(c_1)c_1 \subset t(c_2)c_2 \setminus \operatorname {\mathrm {ret}}(t)(c_2)c_2$
. However, here we appeal to a property of the retraction map that is easily checked by induction. For each
$t(c_1)c_1 \subset t(c_2)c_2 \setminus \operatorname {\mathrm {ret}}(t)(c_2)c_2$
. However, here we appeal to a property of the retraction map that is easily checked by induction. For each
![]() $c \in C(t)$
, we have that
$c \in C(t)$
, we have that
 $$ \begin{align} \bigcup_{c_0 \in C(t)_{<c}} t(c_0)c_0 = \bigcup_{c_0 \in C(t)_{<c}} \operatorname{\mathrm{ret}}(t)(c_0)c_0. \end{align} $$
$$ \begin{align} \bigcup_{c_0 \in C(t)_{<c}} t(c_0)c_0 = \bigcup_{c_0 \in C(t)_{<c}} \operatorname{\mathrm{ret}}(t)(c_0)c_0. \end{align} $$
Moreover, the assumption that
![]() $i < j$
implies that
$i < j$
implies that
![]() $c_2 \in C(t)_{<c_1}$
, as the tiles are placed in order of largest to smallest. In that case, we have that
$c_2 \in C(t)_{<c_1}$
, as the tiles are placed in order of largest to smallest. In that case, we have that
 $$ \begin{align*} \operatorname{\mathrm{ret}}(t)(c_1)c_1 \subset t(c_1)c_1 \subset t(c_2)c_2 \subset \bigcup_{c_0 \in C(t)_{<c_1}} t(c_0)c_0. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{ret}}(t)(c_1)c_1 \subset t(c_1)c_1 \subset t(c_2)c_2 \subset \bigcup_{c_0 \in C(t)_{<c_1}} t(c_0)c_0. \end{align*} $$
This, together with property (R1), implies that
![]() $\operatorname {\mathrm {ret}}(t)(c_1)c_1$
intersects
$\operatorname {\mathrm {ret}}(t)(c_1)c_1$
intersects
![]() $\operatorname {\mathrm {ret}}(t)(c_0)c_0$
for some
$\operatorname {\mathrm {ret}}(t)(c_0)c_0$
for some
![]() $c_0 \in C(t)_{<c_1}$
, which contradicts the disjointness of
$c_0 \in C(t)_{<c_1}$
, which contradicts the disjointness of
![]() $\operatorname {\mathrm {ret}}(t)$
.
$\operatorname {\mathrm {ret}}(t)$
.
This covers all cases, so we conclude that
![]() $C(t)$
must be L-separated for every
$C(t)$
must be L-separated for every
![]() $t \in T$
. With this, we have verified all properties for the theorem not already proved in [Reference Downarowicz and Huczek6].
$t \in T$
. With this, we have verified all properties for the theorem not already proved in [Reference Downarowicz and Huczek6].
One sees as a consequence of the above theorem that X factors directly onto
![]() $\operatorname {\mathrm {ret}}(T)$
, a system of disjoint quasi-tilings with arbitrarily large shapes and near-covering of G. This is stated by Downarowicz and Huczek [Reference Downarowicz and Huczek6, Corollary 3.5]. However, one has to give up control of the number of tile shapes in exchange for perfect disjointness of the tiles.
$\operatorname {\mathrm {ret}}(T)$
, a system of disjoint quasi-tilings with arbitrarily large shapes and near-covering of G. This is stated by Downarowicz and Huczek [Reference Downarowicz and Huczek6, Corollary 3.5]. However, one has to give up control of the number of tile shapes in exchange for perfect disjointness of the tiles.
For our purposes, we shall make use of the intermediate factor T. Each
![]() $t \in T$
carries all of the information needed to construct a disjoint quasi-tiling (by way of taking the retraction
$t \in T$
carries all of the information needed to construct a disjoint quasi-tiling (by way of taking the retraction
![]() $\operatorname {\mathrm {ret}}(t)$
); we retain control of the ‘density’ of that information by controlling the number of tile shapes and distributing the centers of the tiles arbitrarily sparsely throughout the group.
$\operatorname {\mathrm {ret}}(t)$
); we retain control of the ‘density’ of that information by controlling the number of tile shapes and distributing the centers of the tiles arbitrarily sparsely throughout the group.
2.4. Comparison property
In this section, we turn our attention to the case where G has the comparison property. In short, with the comparison property, one may demonstrate that if
![]() $\varepsilon $
is sufficiently small and if the shapes in
$\varepsilon $
is sufficiently small and if the shapes in
![]() ${\mathcal S}$
are sufficiently large, then the subshift T in Theorem 2.9 factors onto a system
${\mathcal S}$
are sufficiently large, then the subshift T in Theorem 2.9 factors onto a system
![]() $T_1$
of exact tilings.
$T_1$
of exact tilings.
For a thorough discussion of the comparison property for countable amenable groups and its consequences, see [Reference Downarowicz and Zhang8]. Here, we only repeat that the class of groups with the comparison property includes all countable groups with no finitely generated subgroup of exponential growth, and it is still unknown whether there exists a countable amenable group without the comparison property.
The following theorem is a consequence of the main results of [Reference Downarowicz and Zhang9, Proposition 4.3, Theorem 4.7], also appearing in [Reference Downarowicz and Zhang8, Proposition 6.10, Theorem 6.12]. We state the result in this form for convenience; this is the form in which we shall appeal to the comparison property later in our construction.
Given a subshift T, suppose we assign to each
![]() $t\in T$
a subset
$t\in T$
a subset
![]() $G_t \subset G$
. We can encode each subset
$G_t \subset G$
. We can encode each subset
![]() $G_t$
by its indicator function
$G_t$
by its indicator function
![]() $\chi _{G_t} \in \{0,1\}^G$
. We say that the assignment
$\chi _{G_t} \in \{0,1\}^G$
. We say that the assignment
![]() $t \mapsto G_t$
is continuous and shift-commuting if the map
$t \mapsto G_t$
is continuous and shift-commuting if the map
![]() $t\mapsto \chi _{G_t}$
is continuous and shift-commuting in the usual sense (Definition 2.12). Equivalently, there is a finite subset
$t\mapsto \chi _{G_t}$
is continuous and shift-commuting in the usual sense (Definition 2.12). Equivalently, there is a finite subset
![]() $F \subset G$
and a collection of patterns
$F \subset G$
and a collection of patterns
![]() $\mathcal {G} \subset {\mathcal P}(F,T)$
such that for every
$\mathcal {G} \subset {\mathcal P}(F,T)$
such that for every
![]() $g\in G$
and
$g\in G$
and
![]() $t \in T$
, we have
$t \in T$
, we have
![]() $g\in G_t$
if and only if
$g\in G_t$
if and only if
![]() $\sigma ^g(t)(F) \in \mathcal {G}$
.
$\sigma ^g(t)(F) \in \mathcal {G}$
.
Theorem 2.10. Suppose G has the comparison property. Let T be a subshift over G and suppose for every
![]() $t \in T$
, we have corresponding disjoint subsets
$t \in T$
, we have corresponding disjoint subsets
![]() $A_t$
,
$A_t$
,
![]() $B_t\subset G$
such that:
$B_t\subset G$
such that:
-
(1) the assignments
 $t \mapsto A_t$
,
$t \mapsto A_t$
,
 $B_t$
are continuous and shift commuting; and
$B_t$
are continuous and shift commuting; and -
(2) there exists an
 $\varepsilon> 0$
such that
$\varepsilon> 0$
such that
 $\underline {D}(B_t) - \overline {D}(A_t)> \varepsilon $
for every
$\underline {D}(B_t) - \overline {D}(A_t)> \varepsilon $
for every
 $t\in T$
.
$t\in T$
.
Then there is a family of injections
![]() $\phi _t : A_t \to B_t$
induced by a block code, in the sense that there is a finite subset
$\phi _t : A_t \to B_t$
induced by a block code, in the sense that there is a finite subset
![]() $F \subset G$
and a function
$F \subset G$
and a function
![]() $\Phi : {\mathcal P}(F,T) \to F$
such that for every
$\Phi : {\mathcal P}(F,T) \to F$
such that for every
![]() $t\in T$
and every
$t\in T$
and every
![]() $g\in A_t$
, it holds that
$g\in A_t$
, it holds that
The following theorem is implicitly proved in both [Reference Downarowicz and Zhang9, Theorem 6.3] and [Reference Downarowicz and Zhang8, Theorem 7.5]. The proof, a construction that we adapt in part of our Theorem 3.5, relies on the characterization of the comparison property given in the previous theorem. We appeal to each of these theorems later, using Theorem 2.10 in Theorem 3.5 and using Theorem 2.11 in Theorem 3.2.
Theorem 2.11. Let G be a countable amenable group with the comparison property. For every finite subset
![]() $K \subset G$
and
$K \subset G$
and
![]() $\varepsilon> 0$
, there is a
$\varepsilon> 0$
, there is a
![]() $\delta> 0$
such that, if T is a system of disjoint,
$\delta> 0$
such that, if T is a system of disjoint,
![]() $(1-\delta )$
-covering quasi-tilings with
$(1-\delta )$
-covering quasi-tilings with
![]() $(K,\delta )$
-invariant shapes, then T factors onto a system
$(K,\delta )$
-invariant shapes, then T factors onto a system
![]() $T_1$
of exact tilings with
$T_1$
of exact tilings with
![]() $(K,\varepsilon )$
-invariant shapes, by way of a factor map
$(K,\varepsilon )$
-invariant shapes, by way of a factor map
![]() $\operatorname {\mathrm {ex}} : T \to T_1$
such that
$\operatorname {\mathrm {ex}} : T \to T_1$
such that
![]() $C(t) = C(\operatorname {\mathrm {ex}}(t))$
for every
$C(t) = C(\operatorname {\mathrm {ex}}(t))$
for every
![]() $t\in T$
and
$t\in T$
and
![]() $t(c) \subset \operatorname {\mathrm {ex}}(t)(c)$
for every
$t(c) \subset \operatorname {\mathrm {ex}}(t)(c)$
for every
![]() $c\in C(t)$
.
$c\in C(t)$
.
3. Theorems
3.1. Target system
To construct an embedding from a given subshift X into a given subshift Y, it will first be necessary for our construction to pass to a subsystem
![]() $Y_0 \subset Y$
in a way that preserves most of the conditions on Y. In this section, we construct that subshift
$Y_0 \subset Y$
in a way that preserves most of the conditions on Y. In this section, we construct that subshift
![]() $Y_0$
.
$Y_0$
.
In the following definition, we borrow a phrase from functional analysis.
Definition 3.1. (Separating elements)
Let G be a discrete group. We say that a subshift Y over G separates elements of G if for every pair of distinct elements
![]() $g_1$
,
$g_1$
,
![]() $g_2 \in G$
, there is a point
$g_2 \in G$
, there is a point
![]() $y\in Y$
such that
$y\in Y$
such that
![]() $y(g_1) \neq y(g_2)$
. Because Y is shift-invariant, this is true if and only if it holds that for each
$y(g_1) \neq y(g_2)$
. Because Y is shift-invariant, this is true if and only if it holds that for each
![]() $g\neq e$
, there is a point
$g\neq e$
, there is a point
![]() $y\in Y$
such that
$y\in Y$
such that
![]() $y(e) \neq y(g)$
.
$y(e) \neq y(g)$
.
This condition is not invariant under topological conjugacy. However, a subshift
![]() $Y_1$
is conjugate to a subshift Y that separates elements of G if and only if there is a finite subset
$Y_1$
is conjugate to a subshift Y that separates elements of G if and only if there is a finite subset
![]() $F\subset G$
such that, for every
$F\subset G$
such that, for every
![]() $g\neq e$
, there is a point
$g\neq e$
, there is a point
![]() $y_1 \in Y_1$
with
$y_1 \in Y_1$
with
![]() $\sigma ^g(y_1)(F) \neq y_1(F)$
. The forward implication follows from the Curtis–Lyndon–Hedlund theorem, and the converse implication follows from passing to a higher block presentation of Y.
$\sigma ^g(y_1)(F) \neq y_1(F)$
. The forward implication follows from the Curtis–Lyndon–Hedlund theorem, and the converse implication follows from passing to a higher block presentation of Y.
This condition is similar to the condition that Y has no global period, meaning that there is no element
![]() $g \neq e$
such that
$g \neq e$
such that
![]() $\sigma ^g(y) = y$
for every
$\sigma ^g(y) = y$
for every
![]() $y \in Y$
(equivalently, the shift action
$y \in Y$
(equivalently, the shift action
![]() $\sigma $
is faithful on Y). If a subshift Y separates elements of G, then Y necessarily has no global period. The converse holds when G is abelian, but not in general. When Y is strongly irreducible, we have the following partial converse.
$\sigma $
is faithful on Y). If a subshift Y separates elements of G, then Y necessarily has no global period. The converse holds when G is abelian, but not in general. When Y is strongly irreducible, we have the following partial converse.
Lemma 3.1. Let G be a discrete group and let Y be a non-trivial strongly irreducible subshift over G. If Y has no global period, then Y is conjugate to a subshift that separates elements of G.
Proof. Let
![]() $K\subset G$
be a finite subset containing e that witnesses the strong irreducibility of Y and write
$K\subset G$
be a finite subset containing e that witnesses the strong irreducibility of Y and write
![]() $K = \{e,k_1,k_2,\ldots ,k_n\}$
. Because Y has no global period, for each
$K = \{e,k_1,k_2,\ldots ,k_n\}$
. Because Y has no global period, for each
![]() $i \leq n$
, there exists a point
$i \leq n$
, there exists a point
![]() $y_i \in Y$
and an element
$y_i \in Y$
and an element
![]() $g_i \in G$
such that
$g_i \in G$
such that
![]() $\sigma ^{k_i}(y_i)(g_i) \neq y_i(g_i)$
.
$\sigma ^{k_i}(y_i)(g_i) \neq y_i(g_i)$
.
Let
![]() $F = \{e, g_1, g_2, \ldots , g_n\}$
and let
$F = \{e, g_1, g_2, \ldots , g_n\}$
and let
![]() $g\in G\setminus \{e\}$
be chosen arbitrarily. Because Y is non-trivial and strongly irreducible, if
$g\in G\setminus \{e\}$
be chosen arbitrarily. Because Y is non-trivial and strongly irreducible, if
![]() $g \in G \setminus K$
, then we may construct a point
$g \in G \setminus K$
, then we may construct a point
![]() $y \in Y$
such that
$y \in Y$
such that
![]() $y(e) \neq y(g)$
, in which case
$y(e) \neq y(g)$
, in which case
![]() $y(F) \neq \sigma ^g(y)(F)$
. If instead
$y(F) \neq \sigma ^g(y)(F)$
. If instead
![]() $g = k_i$
for some
$g = k_i$
for some
![]() $i\leq n$
, then the fact that
$i\leq n$
, then the fact that
![]() $y_i(g_i) \neq \sigma ^{k_i}(y_i)(g_i)$
implies that
$y_i(g_i) \neq \sigma ^{k_i}(y_i)(g_i)$
implies that
![]() $y_i(F) \neq \sigma ^g(y_i)(F)$
.
$y_i(F) \neq \sigma ^g(y_i)(F)$
.
We have shown that for every
![]() $g\neq e$
, there is a point
$g\neq e$
, there is a point
![]() $y\in Y$
for which
$y\in Y$
for which
![]() $y(F) \neq \sigma ^g(y)(F)$
, in which case Y is conjugate to a subshift that separates elements of G by the observation in the paragraph following Definition 3.1, and the lemma is completed.
$y(F) \neq \sigma ^g(y)(F)$
, in which case Y is conjugate to a subshift that separates elements of G by the observation in the paragraph following Definition 3.1, and the lemma is completed.
The previous lemma demonstrates that when Y is strongly irreducible, we may use conjugacy to pass back and forth between the condition that Y has no global period and the condition that Y separates elements of G. Indeed, in the proof of Theorem 3.5, we shall appeal to the fact that Y has no global period to replace Y with a conjugate subshift that separates elements of G.
It is not in general true that a strongly irreducible subshift automatically has no global period. However, as noted in the proof of the above lemma, if a subshift Y is non-trivial and strongly irreducible as witnessed by
![]() $K \subset G$
, then for each
$K \subset G$
, then for each
![]() $g\notin K$
, there is a point
$g\notin K$
, there is a point
![]() $y\in Y$
such that
$y\in Y$
such that
![]() $y \neq \sigma ^g(y)$
. This implies that any element that is a global period of Y must belong to K (moreover, the subgroup of G consisting of all global periods of Y must be contained in K). In this sense, to assume that a strongly irreducible subshift Y also has no global period only imposes finitely many additional conditions on Y.
$y \neq \sigma ^g(y)$
. This implies that any element that is a global period of Y must belong to K (moreover, the subgroup of G consisting of all global periods of Y must be contained in K). In this sense, to assume that a strongly irreducible subshift Y also has no global period only imposes finitely many additional conditions on Y.
From this, we also see that when G is a torsion-free group (such as
![]() $\mathbb {Z}^d$
), then a non-trivial strongly irreducible subshift over G automatically has no global period. In fact, it is not difficult to show that a strongly irreducible subshift over a group G with no element of finite order must necessarily separate elements of G.
$\mathbb {Z}^d$
), then a non-trivial strongly irreducible subshift over G automatically has no global period. In fact, it is not difficult to show that a strongly irreducible subshift over a group G with no element of finite order must necessarily separate elements of G.
We now proceed with the main construction for this section. Given a strongly irreducible SFT Y that separates elements of G and has positive entropy, the following theorem produces a subsystem
![]() $Y_0 \subset Y$
that is also strongly irreducible, separates elements of G, and has entropy in any arbitrary subinterval of
$Y_0 \subset Y$
that is also strongly irreducible, separates elements of G, and has entropy in any arbitrary subinterval of
![]() $[0,h(Y)]$
. The construction presented below is a modification of the construction presented in [Reference Bland, McGoff and Pavlov2, Theorem 4.1]. Here we invoke the comparison property to construct a strongly irreducible system of exact tilings of G.
$[0,h(Y)]$
. The construction presented below is a modification of the construction presented in [Reference Bland, McGoff and Pavlov2, Theorem 4.1]. Here we invoke the comparison property to construct a strongly irreducible system of exact tilings of G.
Theorem 3.2. Let G be a countable amenable group with the comparison property, let Y be a strongly irreducible SFT over G that separates elements of G, and let
![]() $\tilde {Y} \subset Y$
be a subshift satisfying
$\tilde {Y} \subset Y$
be a subshift satisfying
![]() $h(\tilde {Y}) < h(Y)$
. For every subinterval
$h(\tilde {Y}) < h(Y)$
. For every subinterval
![]() $(a,b) \subset [h(\tilde {Y}), h(Y)]$
, there is a strongly irreducible subshift
$(a,b) \subset [h(\tilde {Y}), h(Y)]$
, there is a strongly irreducible subshift
![]() $Y_0$
that separates elements of G and satisfies
$Y_0$
that separates elements of G and satisfies
![]() $\tilde {Y} \subset Y_0 \subset Y$
and
$\tilde {Y} \subset Y_0 \subset Y$
and
![]() $a < h(Y_0) < b$
.
$a < h(Y_0) < b$
.
Proof. Let
![]() ${\mathcal A}$
be a finite alphabet such that
${\mathcal A}$
be a finite alphabet such that
![]() $Y \subset {\mathcal A}^G$
. Let
$Y \subset {\mathcal A}^G$
. Let
![]() $K \subset G$
be a finite subset with
$K \subset G$
be a finite subset with
![]() ${e \in K}$
chosen to witness Y as a strongly irreducible SFT. We shall abbreviate
${e \in K}$
chosen to witness Y as a strongly irreducible SFT. We shall abbreviate
![]() $\operatorname {\mathrm {int}}^n F = \operatorname {\mathrm {int}}_{K^n} F$
and
$\operatorname {\mathrm {int}}^n F = \operatorname {\mathrm {int}}_{K^n} F$
and
![]() $\partial ^n F = \partial _{K^n} F$
for each natural
$\partial ^n F = \partial _{K^n} F$
for each natural
![]() $n \in \mathbb {N}$
and finite subset
$n \in \mathbb {N}$
and finite subset
![]() $F \subset G$
for the remainder of this proof. We shall also abbreviate
$F \subset G$
for the remainder of this proof. We shall also abbreviate
![]() $\partial ^n p = p(\partial ^n F)$
for each pattern p of shape F.
$\partial ^n p = p(\partial ^n F)$
for each pattern p of shape F.
Choose
![]() $\varepsilon> 0$
such that
$\varepsilon> 0$
such that
 $$ \begin{align*} \varepsilon < \min\bigg(\frac{b-a}{3+\log 2 + 2\log\!|{\mathcal A}|}, \frac{b-a}{5+4\log\!|{\mathcal A}|}\bigg). \end{align*} $$
$$ \begin{align*} \varepsilon < \min\bigg(\frac{b-a}{3+\log 2 + 2\log\!|{\mathcal A}|}, \frac{b-a}{5+4\log\!|{\mathcal A}|}\bigg). \end{align*} $$
It is a theorem of Frisch and Tamuz [Reference Frisch and Tamuz10, Theorem 2.1] that for any
![]() $(K,\delta )$
, there exists a strongly irreducible system of disjoint,
$(K,\delta )$
, there exists a strongly irreducible system of disjoint,
![]() $(1-\delta )$
-covering quasi-tilings of G whose every shape is
$(1-\delta )$
-covering quasi-tilings of G whose every shape is
![]() $(K,\delta )$
-invariant and whose entropy is less than
$(K,\delta )$
-invariant and whose entropy is less than
![]() $\delta $
. This, in combination with Theorem 2.11 and the fact that strong irreducibility is preserved under factor maps, implies the following. There exists a finite collection of shapes
$\delta $
. This, in combination with Theorem 2.11 and the fact that strong irreducibility is preserved under factor maps, implies the following. There exists a finite collection of shapes
![]() ${\mathcal S}$
and a strongly irreducible system
${\mathcal S}$
and a strongly irreducible system
![]() $T \subset \Lambda ({\mathcal S})^G$
of exact tilings of G such that
$T \subset \Lambda ({\mathcal S})^G$
of exact tilings of G such that
![]() $h(T) < \varepsilon $
and every shape
$h(T) < \varepsilon $
and every shape
![]() $S\in {\mathcal S}$
satisfies the following:
$S\in {\mathcal S}$
satisfies the following:
-
(S1)
 $K \subset \operatorname {\mathrm {int}}^2 S$
;
$K \subset \operatorname {\mathrm {int}}^2 S$
; -
(S2)
 $|S|> \varepsilon ^{-1}$
and
$|S|> \varepsilon ^{-1}$
and
 $2|S| < e^{\varepsilon |S|}$
;
$2|S| < e^{\varepsilon |S|}$
; -
(S3)
 $|\partial ^2 S| < \varepsilon |S|$
; and
$|\partial ^2 S| < \varepsilon |S|$
; and -
(S4)
 $h(S,\tilde {Y}) < h(\tilde {Y}) + \varepsilon $
.
$h(S,\tilde {Y}) < h(\tilde {Y}) + \varepsilon $
.
For the majority of this proof, we operate primarily in the product system
![]() $Z_0 = Y \times T$
. For each finite subset
$Z_0 = Y \times T$
. For each finite subset
![]() $F \subset G$
and pattern
$F \subset G$
and pattern
![]() $p \in {\mathcal P}(F,Z_0)$
, we shall write
$p \in {\mathcal P}(F,Z_0)$
, we shall write
![]() $p = (p^Y,p^T)$
, where
$p = (p^Y,p^T)$
, where
![]() $p^Y \in {\mathcal P}(F,Y)$
and
$p^Y \in {\mathcal P}(F,Y)$
and
![]() $p^T \in {\mathcal P}(F,T)$
. If
$p^T \in {\mathcal P}(F,T)$
. If
![]() $F = S$
for some
$F = S$
for some
![]() $S \in {\mathcal S}$
, then we shall describe p as a ‘block’.
$S \in {\mathcal S}$
, then we shall describe p as a ‘block’.
A block
![]() $b \in {\mathcal P}(S,Z_0)$
is called aligned if
$b \in {\mathcal P}(S,Z_0)$
is called aligned if
![]() $b^T(e) = S$
(note
$b^T(e) = S$
(note
![]() $e\in K$
and
$e\in K$
and
![]() $K\subset S$
by property (S1)). Note that if b is aligned, then
$K\subset S$
by property (S1)). Note that if b is aligned, then
![]() $b^T(s) = \varnothing $
for each
$b^T(s) = \varnothing $
for each
![]() $s \in S\setminus \{e\}$
, by the fact that every tiling
$s \in S\setminus \{e\}$
, by the fact that every tiling
![]() $t\in T$
is disjoint. For a given subshift
$t\in T$
is disjoint. For a given subshift
![]() $Z \subset Z_0$
, we denote the subcollection of all aligned blocks of shape S allowed in Z by
$Z \subset Z_0$
, we denote the subcollection of all aligned blocks of shape S allowed in Z by
where the superscript a identifies the subcollection.
Let
![]() $\pi : Z_0 \to Y$
be the projection map defined by
$\pi : Z_0 \to Y$
be the projection map defined by
![]() $\pi (y,t) = y$
for each
$\pi (y,t) = y$
for each
![]() $(y,t) \in Z_0$
, which is a homomorphism. For each subshift
$(y,t) \in Z_0$
, which is a homomorphism. For each subshift
![]() $Z \subset Z_0$
and each fixed
$Z \subset Z_0$
and each fixed
![]() $z = (y,t) \in Z$
, we have
$z = (y,t) \in Z$
, we have
![]() $y = \pi (z) \in \pi (Z)$
and
$y = \pi (z) \in \pi (Z)$
and
![]() $t \in T$
, thus
$t \in T$
, thus
![]() $Z \subset \pi (Z) \times T$
. Consequently, for each subshift
$Z \subset \pi (Z) \times T$
. Consequently, for each subshift
![]() $Z \subset Z_0$
, it holds that
$Z \subset Z_0$
, it holds that
where above we have used Lemma 2.7 and the fact that
![]() $h(T) < \varepsilon $
.
$h(T) < \varepsilon $
.
Let
![]() $S \in {\mathcal S}$
be fixed. Here we choose and fix a collection of aligned blocks
$S \in {\mathcal S}$
be fixed. Here we choose and fix a collection of aligned blocks
![]() $\mathcal {W}(S) \subset {\mathcal P}^a(S,Z_0)$
. We shall refer to these as ‘witness patterns’, because they will later allow us to demonstrate (‘witness’) for each
$\mathcal {W}(S) \subset {\mathcal P}^a(S,Z_0)$
. We shall refer to these as ‘witness patterns’, because they will later allow us to demonstrate (‘witness’) for each
![]() $g \in G$
a point
$g \in G$
a point
![]() $z \in Z_0$
such that
$z \in Z_0$
such that
![]() $z^Y(e) \neq z^Y(g)$
. These witness patterns shall be of three types.
$z^Y(e) \neq z^Y(g)$
. These witness patterns shall be of three types.
For the first type, let
![]() $s\in S\setminus \{e\}$
be arbitrary. Because Y separates elements of G, there is a pattern
$s\in S\setminus \{e\}$
be arbitrary. Because Y separates elements of G, there is a pattern
![]() $b^Y \in {\mathcal P}(S,Y)$
such that
$b^Y \in {\mathcal P}(S,Y)$
such that
![]() $b^Y(e) \neq b^Y(s)$
. If
$b^Y(e) \neq b^Y(s)$
. If
![]() $b^T \in {\mathcal P}(S,T)$
is given by
$b^T \in {\mathcal P}(S,T)$
is given by
![]() $b^T(e) = S$
and
$b^T(e) = S$
and
![]() $b^T(s) = \varnothing $
for each
$b^T(s) = \varnothing $
for each
![]() $s \in S\setminus \{e\}$
, then
$s \in S\setminus \{e\}$
, then
![]() $b = (b^Y, b^T)$
is an allowed block in
$b = (b^Y, b^T)$
is an allowed block in
![]() $Z_0$
that satisfies
$Z_0$
that satisfies
![]() $b^Y(e) \neq b^Y(s)$
. For each
$b^Y(e) \neq b^Y(s)$
. For each
![]() $s \in S\setminus \{e\}$
, pick and save one such block b to the collection
$s \in S\setminus \{e\}$
, pick and save one such block b to the collection
![]() $\mathcal {W}(S)$
.
$\mathcal {W}(S)$
.
For the second type, let
![]() $0 \in {\mathcal A}$
be a distinguished symbol of the alphabet. For every
$0 \in {\mathcal A}$
be a distinguished symbol of the alphabet. For every
![]() $y\in Y$
, we can find a block
$y\in Y$
, we can find a block
![]() $b \in {\mathcal P}(S,Z_0)$
such that
$b \in {\mathcal P}(S,Z_0)$
such that
![]() $b(e) = (0,S)$
and
$b(e) = (0,S)$
and
![]() $b^Y(\partial ^2 S) = y(\partial ^2 S)$
. This is because Y is strongly irreducible of parameter K and property (S1). For each pattern
$b^Y(\partial ^2 S) = y(\partial ^2 S)$
. This is because Y is strongly irreducible of parameter K and property (S1). For each pattern
![]() $y(\partial ^2 S) \in {\mathcal P}(\partial ^2 S, Y)$
, pick and save one such block b to the collection
$y(\partial ^2 S) \in {\mathcal P}(\partial ^2 S, Y)$
, pick and save one such block b to the collection
![]() $\mathcal {W}(S)$
.
$\mathcal {W}(S)$
.
For the third type, let
![]() $1 \in {\mathcal A}$
be a distinguished symbol different from
$1 \in {\mathcal A}$
be a distinguished symbol different from
![]() $0$
. For each
$0$
. For each
![]() $s \in S$
, we can find a block
$s \in S$
, we can find a block
![]() $b \in {\mathcal P}(S,Y)$
such that
$b \in {\mathcal P}(S,Y)$
such that
![]() $b^T(e) = S$
and
$b^T(e) = S$
and
![]() $b^Y(s) = 1$
. For each
$b^Y(s) = 1$
. For each
![]() $s \in S$
, pick and save one such block b to the collection
$s \in S$
, pick and save one such block b to the collection
![]() $\mathcal {W}(S)$
. This completes the description of the collection
$\mathcal {W}(S)$
. This completes the description of the collection
![]() $\mathcal {W}(S)$
. Note that
$\mathcal {W}(S)$
. Note that
![]() $|\mathcal {W}(S)| \leq 2|S| + {\mathcal A}^{|\partial ^2 S|} < e^{\varepsilon |S|} \cdot |{\mathcal A}|^{\varepsilon |S|}$
by properties (S2) and (S3).
$|\mathcal {W}(S)| \leq 2|S| + {\mathcal A}^{|\partial ^2 S|} < e^{\varepsilon |S|} \cdot |{\mathcal A}|^{\varepsilon |S|}$
by properties (S2) and (S3).
We now construct a descending chain of subshifts
![]() $(Z_n)_n$
of
$(Z_n)_n$
of
![]() $Z_0$
and claim that the subshift
$Z_0$
and claim that the subshift
![]() $Y_0$
desired for the theorem shall be given by
$Y_0$
desired for the theorem shall be given by
![]() $Y_0 = \pi (Z_n)$
for some
$Y_0 = \pi (Z_n)$
for some
![]() $n \leq N$
. Suppose for induction that
$n \leq N$
. Suppose for induction that
![]() $Z_n \subset Z_0$
has been constructed for
$Z_n \subset Z_0$
has been constructed for
![]() $n \geq 0$
. If there exists a shape
$n \geq 0$
. If there exists a shape
![]() $S_n \in {\mathcal S}$
and an aligned block
$S_n \in {\mathcal S}$
and an aligned block
![]() $\beta _n \in {\mathcal P}^a(S_n, Z_n)$
such that:
$\beta _n \in {\mathcal P}^a(S_n, Z_n)$
such that:
-
(B1)
 $\beta _n^Y$
does not appear in
$\beta _n^Y$
does not appear in
 $\tilde {Y}$
(
$\tilde {Y}$
(
 $\beta _n^Y \notin {\mathcal P}(S_n, \tilde {Y})$
);
$\beta _n^Y \notin {\mathcal P}(S_n, \tilde {Y})$
); -
(B2)
 $\beta _n$
is not one of the reserved witness patterns (
$\beta _n$
is not one of the reserved witness patterns (
 $\beta _n \notin \mathcal W(S_n)$
); and
$\beta _n \notin \mathcal W(S_n)$
); and -
(B3) there exists an aligned block
 $b \in {\mathcal P}^a(S_n, Z_n)$
with
$b \in {\mathcal P}^a(S_n, Z_n)$
with
 $b \neq \beta _n$
and
$b \neq \beta _n$
and
 $\partial ^2 b = \partial ^2 \beta _n$
,
$\partial ^2 b = \partial ^2 \beta _n$
,
then let
![]() $Z_{n+1} = \langle Z_n \mid \beta _n\rangle $
. If no such block exists for any shape, then the descending chain is finite in length and
$Z_{n+1} = \langle Z_n \mid \beta _n\rangle $
. If no such block exists for any shape, then the descending chain is finite in length and
![]() $Z_n$
is the terminal subshift.
$Z_n$
is the terminal subshift.
In fact, the chain must be finite in length. This is because
![]() $Z_{n+1} \subset Z_n$
implies
$Z_{n+1} \subset Z_n$
implies
![]() ${\mathcal P}(S,Z_{n+1}) \subset {\mathcal P}(S,Z_n)$
for each
${\mathcal P}(S,Z_{n+1}) \subset {\mathcal P}(S,Z_n)$
for each
![]() $S \in {\mathcal S}$
, and
$S \in {\mathcal S}$
, and
![]() ${\mathcal P}(S_n,Z_{n+1}) \sqcup \{\beta _n\} \subset {\mathcal P}(S_n, Z_n)$
for each
${\mathcal P}(S_n,Z_{n+1}) \sqcup \{\beta _n\} \subset {\mathcal P}(S_n, Z_n)$
for each
![]() $n \geq 0$
. Hence, we have that
$n \geq 0$
. Hence, we have that
is a non-negative integer sequence that strictly decreases with n, and therefore must terminate. Let
![]() $N \geq 0$
be the index of the terminal subshift, and note by construction that for each
$N \geq 0$
be the index of the terminal subshift, and note by construction that for each
![]() $S \in {\mathcal S}$
and each aligned block
$S \in {\mathcal S}$
and each aligned block
![]() $b \in {\mathcal P}^a(S, Z_N)$
, either b is uniquely determined by
$b \in {\mathcal P}^a(S, Z_N)$
, either b is uniquely determined by
![]() $\partial ^2 b$
, or
$\partial ^2 b$
, or
![]() $b \in \mathcal {W}(S)$
, or
$b \in \mathcal {W}(S)$
, or
![]() $b^Y \in {\mathcal P}(S,\tilde {Y})$
.
$b^Y \in {\mathcal P}(S,\tilde {Y})$
.
We note the following intermediate lemma that shall be referenced multiple times in the remainder of this proof.
Lemma 3.3. For each
![]() $n < N$
and
$n < N$
and
![]() $(y,t) \in Z_n$
, there is a point
$(y,t) \in Z_n$
, there is a point
![]() $(y^{*},t) \in Z_{n+1}$
satisfying
$(y^{*},t) \in Z_{n+1}$
satisfying
![]() $(y,t)(g) = (y^{*},t)(g)$
for every
$(y,t)(g) = (y^{*},t)(g)$
for every
![]() $g \notin \bigcup _c \operatorname {\mathrm {int}} t(c)c$
, where the union is taken over all
$g \notin \bigcup _c \operatorname {\mathrm {int}} t(c)c$
, where the union is taken over all
![]() $c \in G$
with
$c \in G$
with
![]() $\sigma ^c(y,t) = \beta _n$
.
$\sigma ^c(y,t) = \beta _n$
.
Proof. By property (B3), there is a block
![]() $b \in {\mathcal P}^a(S_n, Z_n)$
such that
$b \in {\mathcal P}^a(S_n, Z_n)$
such that
![]() $b(\partial ^2 S_n) = \beta _n(\partial ^2 S_n)$
. In words, we simply replace every appearance of
$b(\partial ^2 S_n) = \beta _n(\partial ^2 S_n)$
. In words, we simply replace every appearance of
![]() $\beta _n$
in
$\beta _n$
in
![]() $(y,t)$
with b to construct the point
$(y,t)$
with b to construct the point
![]() $(y^{*},t)$
.
$(y^{*},t)$
.
Precisely, let
![]() $(c_k)_k$
enumerate the group elements c for which
$(c_k)_k$
enumerate the group elements c for which
![]() $\sigma ^c(y,t) = \beta _n$
, which is necessarily a subset of the elements c for which
$\sigma ^c(y,t) = \beta _n$
, which is necessarily a subset of the elements c for which
![]() $t(c) = S_n$
because
$t(c) = S_n$
because
![]() $\beta _n$
is aligned. Let
$\beta _n$
is aligned. Let
![]() $y^{*} \in {\mathcal A}^G$
be given by
$y^{*} \in {\mathcal A}^G$
be given by
![]() $y^{*}(g) = b^Y(gc_k^{-1})$
whenever
$y^{*}(g) = b^Y(gc_k^{-1})$
whenever
![]() $g \in S_nc_k$
, and
$g \in S_nc_k$
, and
![]() $y^{*}(g) = y(g)$
for every
$y^{*}(g) = y(g)$
for every
![]() $g \notin \bigcup _k S_nc_k$
. This point is well defined because t is a disjoint tiling.
$g \notin \bigcup _k S_nc_k$
. This point is well defined because t is a disjoint tiling.
Because Y is an SFT of parameter K and by Lemma 2.5, we see that
![]() $y^{*}$
is an allowed point of Y. By construction, for every
$y^{*}$
is an allowed point of Y. By construction, for every
![]() $S \in {\mathcal S}$
and
$S \in {\mathcal S}$
and
![]() $c \in G$
with
$c \in G$
with
![]() $t(c) = S$
, either
$t(c) = S$
, either
![]() $\sigma ^c(y,t)(S) = \sigma ^c(y^{*},t)(S)$
or
$\sigma ^c(y,t)(S) = \sigma ^c(y^{*},t)(S)$
or
![]() $\sigma ^c(y,t) = \beta _n$
and
$\sigma ^c(y,t) = \beta _n$
and
![]() $\sigma ^c(y^{*}, t) = b$
. Consequently, no forbidden block
$\sigma ^c(y^{*}, t) = b$
. Consequently, no forbidden block
![]() $\beta _i$
for any
$\beta _i$
for any
![]() $i < n$
can appear in
$i < n$
can appear in
![]() $(y^{*},t)$
, else that would force an appearance of
$(y^{*},t)$
, else that would force an appearance of
![]() $\beta _i$
in
$\beta _i$
in
![]() $(y,t)$
, where
$(y,t)$
, where
![]() $\beta _i$
is already forbidden. Moreover, the block
$\beta _i$
is already forbidden. Moreover, the block
![]() $\beta _n$
cannot appear in
$\beta _n$
cannot appear in
![]() $(y^{*},t)$
by construction, thus
$(y^{*},t)$
by construction, thus
![]() $(y^{*},t) \in Z_{n+1}$
. Finally, we see by construction that
$(y^{*},t) \in Z_{n+1}$
. Finally, we see by construction that
![]() $(y,t)(g) = (y^{*},t)(g)$
for every
$(y,t)(g) = (y^{*},t)(g)$
for every
![]() $g \not \in \bigcup _c\operatorname {\mathrm {int}} t(c)c$
, where the union is taken over all
$g \not \in \bigcup _c\operatorname {\mathrm {int}} t(c)c$
, where the union is taken over all
![]() $c\in G$
with
$c\in G$
with
![]() $\sigma ^c(y,t) = \beta _n$
as desired, hence we are done.
$\sigma ^c(y,t) = \beta _n$
as desired, hence we are done.
Now continuing the proof of Theorem 3.2, we claim that for each n, the subshift
![]() $\pi (Z_n)$
is strongly irreducible, separates elements of G, and satisfies
$\pi (Z_n)$
is strongly irreducible, separates elements of G, and satisfies
![]() $\tilde {Y} \subset \pi (Z_n) \subset Y$
. Moreover, we claim that
$\tilde {Y} \subset \pi (Z_n) \subset Y$
. Moreover, we claim that
![]() $h(\pi (Z_n)) - h(\pi (Z_{n+1})) < b-a$
for each
$h(\pi (Z_n)) - h(\pi (Z_{n+1})) < b-a$
for each
![]() $n < N$
, and
$n < N$
, and
![]() $h(\pi (Z_N)) - h(\tilde {Y}) < b-a$
.
$h(\pi (Z_N)) - h(\tilde {Y}) < b-a$
.
For
![]() $\tilde {Y} \subset \pi (Z_n) \subset Y$
, let
$\tilde {Y} \subset \pi (Z_n) \subset Y$
, let
![]() $\tilde {y} \in \tilde {Y}$
and
$\tilde {y} \in \tilde {Y}$
and
![]() $t \in T$
be arbitrary, in which case
$t \in T$
be arbitrary, in which case
![]() $(\tilde {y},t) \in Z_0$
. Note that for each
$(\tilde {y},t) \in Z_0$
. Note that for each
![]() $n < N$
, the block
$n < N$
, the block
![]() $\beta _n$
cannot appear in
$\beta _n$
cannot appear in
![]() $(\tilde {y},t)$
, else that would imply that
$(\tilde {y},t)$
, else that would imply that
![]() $\beta _n^Y$
appears in
$\beta _n^Y$
appears in
![]() $\tilde {y}$
, contradicting property (B1). Thus,
$\tilde {y}$
, contradicting property (B1). Thus,
![]() $(\tilde {y},t) \in Z_n$
for each
$(\tilde {y},t) \in Z_n$
for each
![]() ${n \leq N}$
. This demonstrates that
${n \leq N}$
. This demonstrates that
![]() $\tilde {Y} \times T \subset Z_n$
, and in particular
$\tilde {Y} \times T \subset Z_n$
, and in particular
![]() $\tilde {Y} \subset \pi (Z_n) \subset Y$
, for each
$\tilde {Y} \subset \pi (Z_n) \subset Y$
, for each
![]() $n \leq N$
.
$n \leq N$
.
For the strong irreducibility, note that
![]() $Z_0 = Y \times T$
is strongly irreducible because both Y and T are strongly irreducible. For induction, suppose
$Z_0 = Y \times T$
is strongly irreducible because both Y and T are strongly irreducible. For induction, suppose
![]() $Z_n$
is strongly irreducible of parameter
$Z_n$
is strongly irreducible of parameter
![]() $K_n \subset G$
(with
$K_n \subset G$
(with
![]() $e \in K_n$
) for a fixed
$e \in K_n$
) for a fixed
![]() $n < N$
. Let
$n < N$
. Let
![]() $U = \bigcup _{S\in {\mathcal S}} S$
. We claim that
$U = \bigcup _{S\in {\mathcal S}} S$
. We claim that
![]() $Z_{n+1}$
is strongly irreducible of parameter
$Z_{n+1}$
is strongly irreducible of parameter
![]() $UU^{-1} K_n UU^{-1}$
.
$UU^{-1} K_n UU^{-1}$
.
Indeed, let
![]() $(y_1,t_1)$
,
$(y_1,t_1)$
,
![]() $(y_2,t_2) \in Z_{n+1}$
be arbitrary points, and let
$(y_2,t_2) \in Z_{n+1}$
be arbitrary points, and let
![]() $F_1$
,
$F_1$
,
![]() $F_2 \subset G$
be arbitrary finite subsets with
$F_2 \subset G$
be arbitrary finite subsets with
![]() $K_nUU^{-1} F_1 \cap UU^{-1} F_2 = \varnothing $
. As
$K_nUU^{-1} F_1 \cap UU^{-1} F_2 = \varnothing $
. As
![]() $Z_{n+1} \subset Z_n$
and
$Z_{n+1} \subset Z_n$
and
![]() $Z_n$
is strongly irreducible of parameter
$Z_n$
is strongly irreducible of parameter
![]() $K_n$
, there is a point
$K_n$
, there is a point
![]() $(y,t) \in Z_n$
with
$(y,t) \in Z_n$
with
![]() $(y,t)(UU^{-1}F_1) = (y_1,t_1)(UU^{-1}F_1)$
and
$(y,t)(UU^{-1}F_1) = (y_1,t_1)(UU^{-1}F_1)$
and
![]() $(y,t)(UU^{-1}F_2) = (y_2,t_2)(UU^{-1}F_2)$
.
$(y,t)(UU^{-1}F_2) = (y_2,t_2)(UU^{-1}F_2)$
.
Now consider the forbidden block
![]() $\beta _n$
of shape
$\beta _n$
of shape
![]() $S_n \in {\mathcal S}$
. Suppose
$S_n \in {\mathcal S}$
. Suppose
![]() $\sigma ^g(y,t)(S_n) = \beta _n$
for some
$\sigma ^g(y,t)(S_n) = \beta _n$
for some
![]() $g \in G$
with
$g \in G$
with
![]() $S_ng \cap F_1 \neq \varnothing $
. It follows that
$S_ng \cap F_1 \neq \varnothing $
. It follows that
![]() $g \in S_n^{-1} F_1$
, and hence
$g \in S_n^{-1} F_1$
, and hence
![]() $S_ng \subset S_nS_n^{-1} \subset UU^{-1}F_1$
, and hence
$S_ng \subset S_nS_n^{-1} \subset UU^{-1}F_1$
, and hence
![]() $\sigma ^g(y_1,t_1)(S_n) = \sigma ^g(y,t)(S_n) = \beta _n$
, contradicting the fact that
$\sigma ^g(y_1,t_1)(S_n) = \sigma ^g(y,t)(S_n) = \beta _n$
, contradicting the fact that
![]() $(y_1,t_1) \in Z_{n+1}$
and
$(y_1,t_1) \in Z_{n+1}$
and
![]() $\beta _n$
is forbidden in
$\beta _n$
is forbidden in
![]() $Z_{n+1}$
. From this observation (and by an identical argument for
$Z_{n+1}$
. From this observation (and by an identical argument for
![]() $F_2$
), we see that if
$F_2$
), we see that if
![]() $\beta _n$
appears anywhere in
$\beta _n$
appears anywhere in
![]() $(y_0,t)$
, then it does not appear on any tile of t that intersects either
$(y_0,t)$
, then it does not appear on any tile of t that intersects either
![]() $F_1$
or
$F_1$
or
![]() $F_2$
.
$F_2$
.
Let
![]() $(y^{*},t) \in Z_{n+1}$
be the point delivered by Lemma 3.3 as applied to
$(y^{*},t) \in Z_{n+1}$
be the point delivered by Lemma 3.3 as applied to
![]() $(y,t)$
. From the previous paragraph, we have
$(y,t)$
. From the previous paragraph, we have
![]() $(y^{*},t)(F_i) = (y,t)(F_i) = (y_i,t_i)(F_i)$
for each
$(y^{*},t)(F_i) = (y,t)(F_i) = (y_i,t_i)(F_i)$
for each
![]() $i = 1,2$
. We conclude that
$i = 1,2$
. We conclude that
![]() $Z_{n+1}$
is strongly irreducible of parameter
$Z_{n+1}$
is strongly irreducible of parameter
![]() $UU^{-1}K_n UU^{-1}$
, therefore completing the induction. As strong irreducibility is preserved under taking factors, it follows that
$UU^{-1}K_n UU^{-1}$
, therefore completing the induction. As strong irreducibility is preserved under taking factors, it follows that
![]() $\pi (Z_n)$
is strongly irreducible for each
$\pi (Z_n)$
is strongly irreducible for each
![]() $n \leq N$
.
$n \leq N$
.
To see that each
![]() $\pi (Z_n)$
separates elements of G, let
$\pi (Z_n)$
separates elements of G, let
![]() $n \leq N$
and
$n \leq N$
and
![]() $g \neq e$
be fixed. We proceed by cases on g.
$g \neq e$
be fixed. We proceed by cases on g.
If
![]() $g \in S$
for some
$g \in S$
for some
![]() $S \in {\mathcal S}$
, then there is a witness block
$S \in {\mathcal S}$
, then there is a witness block
![]() $b \in \mathcal {W}(S)$
such that
$b \in \mathcal {W}(S)$
such that
![]() $b^Y(e) \neq b^Y(g)$
. Choose and fix
$b^Y(e) \neq b^Y(g)$
. Choose and fix
![]() $(y_0, t) \in Z_0$
such that
$(y_0, t) \in Z_0$
such that
![]() $(y_0,t)(S) = b$
and apply Lemma 3.3 at most N times to produce the point
$(y_0,t)(S) = b$
and apply Lemma 3.3 at most N times to produce the point
![]() $(y_n,t) \in Z_n$
. Note
$(y_n,t) \in Z_n$
. Note
![]() $(y_n,t)(S) = (y_0,t)(S) = b$
, as
$(y_n,t)(S) = (y_0,t)(S) = b$
, as
![]() $b \neq \beta _n$
for every
$b \neq \beta _n$
for every
![]() $n < N$
by property (B2). Consequently,
$n < N$
by property (B2). Consequently,
![]() $y_n \in \pi (Z_n)$
satisfies
$y_n \in \pi (Z_n)$
satisfies
![]() $y_n(e) = b^Y(e) \neq b^Y(g) = y_n(g)$
.
$y_n(e) = b^Y(e) \neq b^Y(g) = y_n(g)$
.
If
![]() $g \notin S$
for any
$g \notin S$
for any
![]() $S \in {\mathcal S}$
, then pick
$S \in {\mathcal S}$
, then pick
![]() $S_0 \in {\mathcal S}$
arbitrarily and fix
$S_0 \in {\mathcal S}$
arbitrarily and fix
![]() $t \in T$
with
$t \in T$
with
![]() $t(e) = S_0$
. Because t is an exact tiling, there is a unique
$t(e) = S_0$
. Because t is an exact tiling, there is a unique
![]() $c \neq e$
such that
$c \neq e$
such that
![]() $g\in t(c)c$
. Let
$g\in t(c)c$
. Let
![]() $S_1 = t(c)$
and write
$S_1 = t(c)$
and write
![]() $g = s_1c$
for some
$g = s_1c$
for some
![]() $s_1 \in S_1 \in {\mathcal S}$
. Recall
$s_1 \in S_1 \in {\mathcal S}$
. Recall
![]() $0$
,
$0$
,
![]() $1 \in {\mathcal A}$
are two distinguished symbols determined in the construction of
$1 \in {\mathcal A}$
are two distinguished symbols determined in the construction of
![]() $\mathcal {W}(S)$
. By construction, there is a witness block
$\mathcal {W}(S)$
. By construction, there is a witness block
![]() ${b_1 \in \mathcal {W}(S_1)}$
with
${b_1 \in \mathcal {W}(S_1)}$
with
![]() $b_1^Y(s_1) = 1$
. Pick any
$b_1^Y(s_1) = 1$
. Pick any
![]() $y \in Y$
with
$y \in Y$
with
![]() $\sigma ^c(y)(S_1) = b_1$
. By construction, there is a witness block
$\sigma ^c(y)(S_1) = b_1$
. By construction, there is a witness block
![]() $b_0 \in \mathcal {W}(S_0)$
with
$b_0 \in \mathcal {W}(S_0)$
with
![]() $b_0^Y(e) = 0$
and
$b_0^Y(e) = 0$
and
![]() $\partial ^2 b_0^Y = y(\partial ^2 S_0)$
. Because Y is an SFT of parameter K and by property (S1) and Lemma 2.5, there is a point
$\partial ^2 b_0^Y = y(\partial ^2 S_0)$
. Because Y is an SFT of parameter K and by property (S1) and Lemma 2.5, there is a point
![]() $y^{*} \in Y$
given by
$y^{*} \in Y$
given by
![]() $y^{*}(S_0) = b_0^Y$
and
$y^{*}(S_0) = b_0^Y$
and
![]() $y^{*}(g) = y(g)$
otherwise. In particular,
$y^{*}(g) = y(g)$
otherwise. In particular,
![]() $\sigma ^c(y^{*})(S_1) = b_1^Y$
. Then, apply Lemma 3.3 at most N times to the initial point
$\sigma ^c(y^{*})(S_1) = b_1^Y$
. Then, apply Lemma 3.3 at most N times to the initial point
![]() $(y^{*},t) \in Z_0$
, thus yielding
$(y^{*},t) \in Z_0$
, thus yielding
![]() $(y_n, t) \in Z_n$
. Observe that
$(y_n, t) \in Z_n$
. Observe that
![]() $(y_n,t)(S_0) = (y^{*},t)(S_0) = b_0$
and
$(y_n,t)(S_0) = (y^{*},t)(S_0) = b_0$
and
![]() $\sigma ^c(y_n,t)(S_1) = \sigma ^c(y^{*},t)(S_1) = b_1$
, because
$\sigma ^c(y_n,t)(S_1) = \sigma ^c(y^{*},t)(S_1) = b_1$
, because
![]() $b_0 \neq \beta _n \neq b_1$
for every
$b_0 \neq \beta _n \neq b_1$
for every
![]() $n < N$
by property (B2). Consequently,
$n < N$
by property (B2). Consequently,
![]() $y_n \in \pi (Z_n)$
satisfies
$y_n \in \pi (Z_n)$
satisfies
![]() $y_n(e) = 0 \neq 1 = y_n(g)$
. This finishes all cases and demonstrates that
$y_n(e) = 0 \neq 1 = y_n(g)$
. This finishes all cases and demonstrates that
![]() $\pi (Z_n)$
separates elements of G for each
$\pi (Z_n)$
separates elements of G for each
![]() $n \leq N$
.
$n \leq N$
.
The proofs that
![]() $h(\pi (Z_n)) - h(\pi (Z_{n+1})) < b-a$
for every
$h(\pi (Z_n)) - h(\pi (Z_{n+1})) < b-a$
for every
![]() $n < N$
and
$n < N$
and
![]() $h(\pi (Z_N)) - h(\tilde {Y}) < b-a$
are nearly identical to arguments appearing in [Reference Bland, McGoff and Pavlov2, Theorem 4.1]. We proceed quickly through the argument here. Choose a finite subset
$h(\pi (Z_N)) - h(\tilde {Y}) < b-a$
are nearly identical to arguments appearing in [Reference Bland, McGoff and Pavlov2, Theorem 4.1]. We proceed quickly through the argument here. Choose a finite subset
![]() $F\subset G$
such that
$F\subset G$
such that
![]() $|h(Z_n) - h(F,Z_n)| < \varepsilon $
for every
$|h(Z_n) - h(F,Z_n)| < \varepsilon $
for every
![]() $n\leq N$
,
$n\leq N$
,
![]() $|h(F,T) - h(T)| < \varepsilon $
(this implies in particular that
$|h(F,T) - h(T)| < \varepsilon $
(this implies in particular that
![]() $h(F,T) < 2\varepsilon $
by choice of T), and
$h(F,T) < 2\varepsilon $
by choice of T), and
![]() $|F \setminus U^{-1}F| < \varepsilon |F|$
, where
$|F \setminus U^{-1}F| < \varepsilon |F|$
, where
![]() $U = \bigcup _{S\in {\mathcal S}} S$
. For each
$U = \bigcup _{S\in {\mathcal S}} S$
. For each
![]() $n \leq N$
, let
$n \leq N$
, let
where the sum is taken over all patterns
![]() $t(F) \in {\mathcal P}(F,T)$
and the product is taken over all
$t(F) \in {\mathcal P}(F,T)$
and the product is taken over all
![]() $c\in C(t) \cap U^{-1}F \cap F$
. For each
$c\in C(t) \cap U^{-1}F \cap F$
. For each
![]() $n \leq N$
, it holds that
$n \leq N$
, it holds that
The first inequality follows from the strong irreducibility of Y in combination with Lemma 3.3. The latter inequality follows from projecting a pattern
![]() $p\in {\mathcal P}(F,Z_n)$
to the interiors of the tiles described by
$p\in {\mathcal P}(F,Z_n)$
to the interiors of the tiles described by
![]() $p^T = t(F) \in {\mathcal P}(F,T)$
that are contained in F. This projection determines p up to the portion of F not covered by those tile interiors, a subset of F of size at most
$p^T = t(F) \in {\mathcal P}(F,T)$
that are contained in F. This projection determines p up to the portion of F not covered by those tile interiors, a subset of F of size at most
![]() $2\varepsilon |F|$
by the combination of the fact that the tiling is exact, the assumed invariance condition on F, and property (S3).
$2\varepsilon |F|$
by the combination of the fact that the tiling is exact, the assumed invariance condition on F, and property (S3).
Moreover, for each
![]() $n < N$
, it holds that
$n < N$
, it holds that
![]() $P(n) \leq 2^{\varepsilon |F|}\cdot P(n+1)$
. This follows from the fact that
$P(n) \leq 2^{\varepsilon |F|}\cdot P(n+1)$
. This follows from the fact that
![]() $|{\mathcal P}^a(\operatorname {\mathrm {int}} S,Z_n)| - |{\mathcal P}^a(\operatorname {\mathrm {int}} S, Z_{n+1})| \leq 1$
(at most one aligned block is removed as one passes from
$|{\mathcal P}^a(\operatorname {\mathrm {int}} S,Z_n)| - |{\mathcal P}^a(\operatorname {\mathrm {int}} S, Z_{n+1})| \leq 1$
(at most one aligned block is removed as one passes from
![]() $Z_n$
to
$Z_n$
to
![]() $Z_{n+1}$
), in combination with the assumed invariance condition on F.
$Z_{n+1}$
), in combination with the assumed invariance condition on F.
The above, in combination with the assumed entropy estimating properties of F, implies that
This, together with the fact that
![]() $h(Z_n) < h(\pi (Z_n)) +\varepsilon $
for each
$h(Z_n) < h(\pi (Z_n)) +\varepsilon $
for each
![]() $n \leq N$
and the choice of
$n \leq N$
and the choice of
![]() $\varepsilon $
, finally gives that
$\varepsilon $
, finally gives that
![]() $h(\pi (Z_n)) - h(\pi (Z_{n+1}) < b-a$
holds for each
$h(\pi (Z_n)) - h(\pi (Z_{n+1}) < b-a$
holds for each
![]() $n < N$
.
$n < N$
.
Next, consider the terminal subshift
![]() $Z_N$
. Recall that for every shape
$Z_N$
. Recall that for every shape
![]() $S\in {\mathcal S}$
, every aligned block
$S\in {\mathcal S}$
, every aligned block
![]() $b\in {\mathcal P}^a(S,Z_N)$
either belongs to
$b\in {\mathcal P}^a(S,Z_N)$
either belongs to
![]() $\mathcal {W}(S)$
, is uniquely determined by
$\mathcal {W}(S)$
, is uniquely determined by
![]() $\partial ^2 b$
, or satisfies
$\partial ^2 b$
, or satisfies
![]() $b^Y \in {\mathcal P}(S,\tilde {Y})$
by construction. Recall also that
$b^Y \in {\mathcal P}(S,\tilde {Y})$
by construction. Recall also that
![]() $|\mathcal {W}(S)| \leq e^{\varepsilon |S|} \cdot |{\mathcal A}|^{\varepsilon |S|}$
. This, together with property (S4), implies that for every shape
$|\mathcal {W}(S)| \leq e^{\varepsilon |S|} \cdot |{\mathcal A}|^{\varepsilon |S|}$
. This, together with property (S4), implies that for every shape
![]() $S\in {\mathcal S}$
, it holds that
$S\in {\mathcal S}$
, it holds that
This, together with the facts that
![]() $h(F,T) < 2\varepsilon $
and
$h(F,T) < 2\varepsilon $
and
![]() $|{\mathcal P}(F,Z_N)| \leq |{\mathcal A}|^{2\varepsilon |F|}\cdot P(N)$
argued earlier, gives us that
$|{\mathcal P}(F,Z_N)| \leq |{\mathcal A}|^{2\varepsilon |F|}\cdot P(N)$
argued earlier, gives us that
in which case it follows that
![]() $h(Z_N) < h(\tilde {Y}) + 5\varepsilon + 4\varepsilon \log \!|{\mathcal A}|$
. This and our choice of
$h(Z_N) < h(\tilde {Y}) + 5\varepsilon + 4\varepsilon \log \!|{\mathcal A}|$
. This and our choice of
![]() $\varepsilon $
finally give that
$\varepsilon $
finally give that
![]() $h(\pi (Z_N)) - h(\tilde {Y}) < b-a$
.
$h(\pi (Z_N)) - h(\tilde {Y}) < b-a$
.
Recall that
![]() $h(\tilde {Y}) < a < b <\! h(Y)$
, and recall also that
$h(\tilde {Y}) < a < b <\! h(Y)$
, and recall also that
![]() $\pi (Z_0)\!=\!Y$
and thus
$\pi (Z_0)\!=\!Y$
and thus
![]() ${h(\pi (Z_0))\!>\!b}$
. We have demonstrated that
${h(\pi (Z_0))\!>\!b}$
. We have demonstrated that
![]() $h(\pi (Z_n)) - h(\pi (Z_{n+1})) < b-a$
for every
$h(\pi (Z_n)) - h(\pi (Z_{n+1})) < b-a$
for every
![]() $n < N$
and
$n < N$
and
![]() $h(\pi (Z_N)) - h(\tilde {Y}) < b-a$
. There must therefore exist at least one
$h(\pi (Z_N)) - h(\tilde {Y}) < b-a$
. There must therefore exist at least one
![]() $n\leq N$
for which
$n\leq N$
for which
![]() $\pi (Z_n)$
satisfies
$\pi (Z_n)$
satisfies
![]() $a < h(\pi (Z_n)) < b$
, thus completing the proof.
$a < h(\pi (Z_n)) < b$
, thus completing the proof.
3.2. Marker patterns
Let Y be a subshift over G. In this section, we construct marker patterns for Y. Marker patterns are patterns
![]() $m \in {\mathcal P}(Y)$
for which appearances of m in any
$m \in {\mathcal P}(Y)$
for which appearances of m in any
![]() $y\in Y$
are separated by arbitrarily large displacements. Ideally, distinct appearances of a marker pattern appear on disjoint regions of G, but in practice, there is potentially some small overlap. The concept of marker patterns originates in the seminal work of Krieger and Boyle that considers the
$y\in Y$
are separated by arbitrarily large displacements. Ideally, distinct appearances of a marker pattern appear on disjoint regions of G, but in practice, there is potentially some small overlap. The concept of marker patterns originates in the seminal work of Krieger and Boyle that considers the
![]() $G = \mathbb {Z}$
case [Reference Boyle3, Reference Krieger13] and the concept has been used by many authors since. For instance, marker patterns were constructed for
$G = \mathbb {Z}$
case [Reference Boyle3, Reference Krieger13] and the concept has been used by many authors since. For instance, marker patterns were constructed for
![]() $G = \mathbb {Z}^d$
by Lightwood [Reference Lightwood14, Lemma 6.3] in the case that Y is an SFT with the uniform filling property that contains a point with a finite orbit. Here we generalize this construction to the case that G is an arbitrary countable amenable group and Y is a strongly irreducible SFT that separates elements of G and has positive entropy. In particular, we do not invoke the comparison property in this construction. This construction, in combination with Theorem 3.2, provides the marker patterns for Y that we need in the proof of our main result.
$G = \mathbb {Z}^d$
by Lightwood [Reference Lightwood14, Lemma 6.3] in the case that Y is an SFT with the uniform filling property that contains a point with a finite orbit. Here we generalize this construction to the case that G is an arbitrary countable amenable group and Y is a strongly irreducible SFT that separates elements of G and has positive entropy. In particular, we do not invoke the comparison property in this construction. This construction, in combination with Theorem 3.2, provides the marker patterns for Y that we need in the proof of our main result.
We construct a marker pattern m here by first constructing an aperiodic point
![]() $y\in Y$
, then taking m to be the pattern of a large-enough shape appearing in y at e. We construct aperiodic points as follows: begin by passing to a subsystem
$y\in Y$
, then taking m to be the pattern of a large-enough shape appearing in y at e. We construct aperiodic points as follows: begin by passing to a subsystem
![]() $Y_1\subset Y$
such that
$Y_1\subset Y$
such that
![]() $h(Y_1) < h(Y)$
, in which case one may find arbitrarily many patterns that do not appear in
$h(Y_1) < h(Y)$
, in which case one may find arbitrarily many patterns that do not appear in
![]() $Y_1$
but that do appear in Y. By beginning with a point in
$Y_1$
but that do appear in Y. By beginning with a point in
![]() $Y_1$
and mixing in one of these ‘forbidden’ patterns from Y (via the strong irreducibility of Y), we obtain a point that lacks all but possibly finitely many periods. Then, we pass to a subsystem
$Y_1$
and mixing in one of these ‘forbidden’ patterns from Y (via the strong irreducibility of Y), we obtain a point that lacks all but possibly finitely many periods. Then, we pass to a subsystem
![]() $Y_0 \subset Y_1$
(which is also assumed to be strongly irreducible and to separate elements of G) from which an auxiliary pattern can be found that lacks precisely that finite set of periods. Mixing this via
$Y_0 \subset Y_1$
(which is also assumed to be strongly irreducible and to separate elements of G) from which an auxiliary pattern can be found that lacks precisely that finite set of periods. Mixing this via
![]() $Y_0$
into our point from before yields the desired aperiodic point.
$Y_0$
into our point from before yields the desired aperiodic point.
Theorem 3.4. Let
![]() $Y_0 \subset Y_1 \subset Y$
be subshifts and suppose that
$Y_0 \subset Y_1 \subset Y$
be subshifts and suppose that
![]() $Y_0$
and Y are strongly irreducible,
$Y_0$
and Y are strongly irreducible,
![]() $Y_0$
separates elements of G, and
$Y_0$
separates elements of G, and
![]() $h(Y_1) < h(Y)$
. For any
$h(Y_1) < h(Y)$
. For any
![]() $r \in \mathbb {N}$
, there exists a finite subset
$r \in \mathbb {N}$
, there exists a finite subset
![]() $M \subset G$
such that for any fixed
$M \subset G$
such that for any fixed
![]() $y_0 \in Y_0$
, there are patterns
$y_0 \in Y_0$
, there are patterns
![]() $m_1, \ldots , m_r \in {\mathcal P}(M,Y) \setminus {\mathcal P}(M, Y_1)$
and points
$m_1, \ldots , m_r \in {\mathcal P}(M,Y) \setminus {\mathcal P}(M, Y_1)$
and points
![]() $y_1, \ldots , y_r \in Y$
satisfying:
$y_1, \ldots , y_r \in Y$
satisfying:
-
(1)
 $m_i$
appears in
$m_i$
appears in
 $y_i$
only at e;
$y_i$
only at e; -
(2)
 $m_i$
does not appear in
$m_i$
does not appear in
 $y_j$
for any
$y_j$
for any
 $j \neq i$
; and
$j \neq i$
; and -
(3)
 $y_i(g) = y_0(g)$
for every
$y_i(g) = y_0(g)$
for every
 $g \notin M$
$g \notin M$
for each
![]() $i = 1, \ldots , r$
.
$i = 1, \ldots , r$
.
Proof. Because
![]() $h(Y_1) < h(Y)$
, there exists a finite subset
$h(Y_1) < h(Y)$
, there exists a finite subset
![]() $F \subset G$
with
$F \subset G$
with
![]() $e \in F$
such that
$e \in F$
such that
![]() $|{\mathcal P}(F,Y) \setminus {\mathcal P}(F,Y_1)|> r$
. Choose and fix r distinct patterns
$|{\mathcal P}(F,Y) \setminus {\mathcal P}(F,Y_1)|> r$
. Choose and fix r distinct patterns
![]() $a_1, \ldots , a_r \in {\mathcal P}(F,Y) \setminus {\mathcal P}(F,Y_1)$
.
$a_1, \ldots , a_r \in {\mathcal P}(F,Y) \setminus {\mathcal P}(F,Y_1)$
.
Choose a finite subset
![]() $K \subset G$
with
$K \subset G$
with
![]() $e \in K$
to witness the strong irreducibility of Y and
$e \in K$
to witness the strong irreducibility of Y and
![]() $Y_0$
. Let
$Y_0$
. Let
![]() $\{e, g_1, \ldots , g_N\}$
be an enumeration of
$\{e, g_1, \ldots , g_N\}$
be an enumeration of
![]() $F^{-1}KF$
. Let
$F^{-1}KF$
. Let
![]() $M_0 = KF$
and suppose for induction that
$M_0 = KF$
and suppose for induction that
![]() $M_{n-1} \subset G$
has been constructed for a fixed
$M_{n-1} \subset G$
has been constructed for a fixed
![]() $n \in [1,N]$
. Because G is infinite, by the pigeonhole principle, there exists an element
$n \in [1,N]$
. Because G is infinite, by the pigeonhole principle, there exists an element
![]() $h_n \in G$
such that
$h_n \in G$
such that
![]() $Kh_n \cup Kh_ng_n$
is disjoint from
$Kh_n \cup Kh_ng_n$
is disjoint from
![]() $M_{n-1}$
. Let
$M_{n-1}$
. Let
![]() $M_n = M_{n-1} \sqcup (Kh_n \cup Kh_ng_n)$
. We claim that
$M_n = M_{n-1} \sqcup (Kh_n \cup Kh_ng_n)$
. We claim that
![]() $M = M_N$
is the subset desired for the theorem. Note that
$M = M_N$
is the subset desired for the theorem. Note that
 $$ \begin{align*} M = KF \sqcup \bigg(\bigsqcup_{n=1}^{N} Kh_n \cup Kh_ng_n\bigg) \end{align*} $$
$$ \begin{align*} M = KF \sqcup \bigg(\bigsqcup_{n=1}^{N} Kh_n \cup Kh_ng_n\bigg) \end{align*} $$
by induction.
Let
![]() $y_0 \in Y_0$
be arbitrary. Let
$y_0 \in Y_0$
be arbitrary. Let
![]() $y_0^{(0)} = y_0$
and suppose for induction that
$y_0^{(0)} = y_0$
and suppose for induction that
![]() $y_0^{(n-1)} \in Y_0$
has been constructed for a fixed
$y_0^{(n-1)} \in Y_0$
has been constructed for a fixed
![]() $n \in [1,N]$
. Because
$n \in [1,N]$
. Because
![]() $Y_0$
separates elements of G, there exists a point
$Y_0$
separates elements of G, there exists a point
![]() $y^{*} \in Y_0$
with
$y^{*} \in Y_0$
with
![]() $y^{*}(h_n) \neq y^{*}(h_ng_n)$
. Because
$y^{*}(h_n) \neq y^{*}(h_ng_n)$
. Because
![]() $Y_0$
is strongly irreducible of parameter K, we may find a point
$Y_0$
is strongly irreducible of parameter K, we may find a point
![]() $y_0^{(n)} \in Y_0$
such that
$y_0^{(n)} \in Y_0$
such that
![]() $y_0^{(n)}(\{h_n,h_ng_n\}) = y^{*}(\{h_n,h_ng_n\})$
and
$y_0^{(n)}(\{h_n,h_ng_n\}) = y^{*}(\{h_n,h_ng_n\})$
and
![]() $y_0^{(n)}(g) = y_0^{(n-1)}(g)$
for every
$y_0^{(n)}(g) = y_0^{(n-1)}(g)$
for every
![]() $g \notin Kh_n \cup Kh_ng_n$
.
$g \notin Kh_n \cup Kh_ng_n$
.
By induction, the point
![]() $y_0^{(N)} \in Y_0$
satisfies
$y_0^{(N)} \in Y_0$
satisfies
![]() $y_0^{(N)}(h_n) \neq y_0^{(N)}(h_ng_n)$
for each
$y_0^{(N)}(h_n) \neq y_0^{(N)}(h_ng_n)$
for each
![]() ${n = 1, \ldots , N}$
and
${n = 1, \ldots , N}$
and
![]() $y_0^{(N)}(g) = y_0(g)$
for every
$y_0^{(N)}(g) = y_0(g)$
for every
![]() $g \notin \bigcup _{n=1}^N Kh_n \cup Kh_ng_n$
.
$g \notin \bigcup _{n=1}^N Kh_n \cup Kh_ng_n$
.
For each
![]() $i = 1, \ldots , r$
, because Y is strongly irreducible of parameter K, we may find a point
$i = 1, \ldots , r$
, because Y is strongly irreducible of parameter K, we may find a point
![]() $y_i \in Y$
such that
$y_i \in Y$
such that
![]() $y_i(F) = a_i$
and
$y_i(F) = a_i$
and
![]() $y_i(g) = y^{(N)}(g)$
for each
$y_i(g) = y^{(N)}(g)$
for each
![]() $g \notin KF$
. Hence, by construction,
$g \notin KF$
. Hence, by construction,
![]() $y_i(h_n) \neq y_i(h_ng_n)$
for each
$y_i(h_n) \neq y_i(h_ng_n)$
for each
![]() $n = 1, \ldots , N$
, and
$n = 1, \ldots , N$
, and
![]() $y_i(g) = y_0(g)$
for each
$y_i(g) = y_0(g)$
for each
![]() ${g \notin M}$
. Finally, let
${g \notin M}$
. Finally, let
![]() $m_i = y_i(M)$
. We claim that these are the patterns and points desired for the theorem. See Figure 1 for an illustration of the construction.
$m_i = y_i(M)$
. We claim that these are the patterns and points desired for the theorem. See Figure 1 for an illustration of the construction.

Figure 1 An illustration of the construction of the marker pattern
![]() $m_i$
. The pattern
$m_i$
. The pattern
![]() $a_i$
is selected from Y to be forbidden in
$a_i$
is selected from Y to be forbidden in
![]() $Y_1$
. Thus,
$Y_1$
. Thus,
![]() $y_i$
has no element of
$y_i$
has no element of
![]() $G \setminus F^{-1}KF$
as a period. Then, small pairs of differing symbols are inductively mixed in (via
$G \setminus F^{-1}KF$
as a period. Then, small pairs of differing symbols are inductively mixed in (via
![]() $Y_0$
) to prevent
$Y_0$
) to prevent
![]() $y_i$
from having any period
$y_i$
from having any period
![]() $g \in F^{-1}KF \setminus \{e\}$
. The shaded exterior is the base point
$g \in F^{-1}KF \setminus \{e\}$
. The shaded exterior is the base point
![]() $y_0 \in Y_0$
.
$y_0 \in Y_0$
.
For property (1), let
![]() $i \leq r$
be fixed. Observe that there is no
$i \leq r$
be fixed. Observe that there is no
![]() $g \in F^{-1}KF\setminus \{e\}$
such that
$g \in F^{-1}KF\setminus \{e\}$
such that
![]() $\sigma ^g(y_i)(M) = y_i(M)$
, as otherwise would contradict the fact that every
$\sigma ^g(y_i)(M) = y_i(M)$
, as otherwise would contradict the fact that every
![]() $g \in F^{-1}KF$
has a corresponding
$g \in F^{-1}KF$
has a corresponding
![]() $h \in M \cap Mg^{-1}$
such that
$h \in M \cap Mg^{-1}$
such that
![]() $y_i(h) \neq y_i(hg)$
. Moreover, if
$y_i(h) \neq y_i(hg)$
. Moreover, if
![]() $g \notin F^{-1}KF$
, then
$g \notin F^{-1}KF$
, then
![]() $Fg$
is disjoint from
$Fg$
is disjoint from
![]() $KF$
, in which case
$KF$
, in which case
![]() $\sigma ^g(y_i)(F) = \sigma ^g(y_0^{(N)})(F)$
. We must therefore have
$\sigma ^g(y_i)(F) = \sigma ^g(y_0^{(N)})(F)$
. We must therefore have
![]() $\sigma ^g(y_i)(F) \neq a_i$
, as otherwise would contradict the fact that
$\sigma ^g(y_i)(F) \neq a_i$
, as otherwise would contradict the fact that
![]() $a_i$
is forbidden in
$a_i$
is forbidden in
![]() $Y_1$
and hence also forbidden in
$Y_1$
and hence also forbidden in
![]() $Y_0$
. Consequently,
$Y_0$
. Consequently,
![]() $\sigma ^g(y_i)(M) = y_i(M)$
only when
$\sigma ^g(y_i)(M) = y_i(M)$
only when
![]() $g = e$
.
$g = e$
.
For property (2), let
![]() $i \neq j$
be fixed. Observe that
$i \neq j$
be fixed. Observe that
![]() $a_j \neq a_i$
implies that
$a_j \neq a_i$
implies that
![]() $y_j(M) \neq y_i(M)$
. Moreover,
$y_j(M) \neq y_i(M)$
. Moreover,
![]() $\sigma ^g(y_j)(M) \neq y_i(M)$
for any
$\sigma ^g(y_j)(M) \neq y_i(M)$
for any
![]() $g \neq e$
by an identical argument as in the previous paragraph. This is because
$g \neq e$
by an identical argument as in the previous paragraph. This is because
![]() $y_j(g) = y_0^{(N)}(g) = y_i(g)$
for every
$y_j(g) = y_0^{(N)}(g) = y_i(g)$
for every
![]() $g \notin KF$
, and both
$g \notin KF$
, and both
![]() $a_i$
and
$a_i$
and
![]() $a_j$
are forbidden in
$a_j$
are forbidden in
![]() $Y_1$
, and hence also forbidden in
$Y_1$
, and hence also forbidden in
![]() $Y_0$
.
$Y_0$
.
Property (3) is true by construction.
One may wonder why we mention the subshift
![]() $Y_1$
at all, instead of merely assuming
$Y_1$
at all, instead of merely assuming
![]() $h(Y_0) < h(Y)$
directly and stating that the marker patterns are forbidden in
$h(Y_0) < h(Y)$
directly and stating that the marker patterns are forbidden in
![]() $Y_0$
. In fact, later on, we shall have some additional structure on
$Y_0$
. In fact, later on, we shall have some additional structure on
![]() $Y_1$
that shall prove useful for our construction. Namely, in the chain of inclusions
$Y_1$
that shall prove useful for our construction. Namely, in the chain of inclusions
![]() $Y_0 \subset Y_1 \subset Y$
, we shall have that
$Y_0 \subset Y_1 \subset Y$
, we shall have that
![]() $Y_0$
is strongly irreducible,
$Y_0$
is strongly irreducible,
![]() $Y_1$
is an SFT, and Y is a strongly irreducible SFT. Then, having the marker patterns forbidden in not only
$Y_1$
is an SFT, and Y is a strongly irreducible SFT. Then, having the marker patterns forbidden in not only
![]() $Y_0$
but also in
$Y_0$
but also in
![]() $Y_1$
shall be significant.
$Y_1$
shall be significant.
3.3. Main result
We are now ready to present our main result. First we briefly outline the proof to come.
Beginning with a strongly aperiodic subshift X, we derive a chain of factors of X in the form
where each
![]() $T_i$
for
$T_i$
for
![]() $i=0,1,2$
is a system of quasi-tilings of G. The foremost system
$i=0,1,2$
is a system of quasi-tilings of G. The foremost system
![]() $T_0$
is one in which the number of shapes is controlled, delivered by Theorem 2.9. The system
$T_0$
is one in which the number of shapes is controlled, delivered by Theorem 2.9. The system
![]() $T_1$
(consisting of retractions of points of
$T_1$
(consisting of retractions of points of
![]() $T_0$
) is one in which each quasi-tiling exhibits large, disjoint tiles that nearly cover G. The lattermost system
$T_0$
) is one in which each quasi-tiling exhibits large, disjoint tiles that nearly cover G. The lattermost system
![]() $T_2$
is a system of exact tilings, and we invoke the comparison property to construct it. Our construction of
$T_2$
is a system of exact tilings, and we invoke the comparison property to construct it. Our construction of
![]() $T_2$
adapts part of the proof of [Reference Downarowicz and Zhang9, Theorem 6.3] (proof also appears in [Reference Downarowicz and Zhang8, Theorem 7.5]). We include the full construction here for the sake of completeness and because we leverage our control over the foremost system
$T_2$
adapts part of the proof of [Reference Downarowicz and Zhang9, Theorem 6.3] (proof also appears in [Reference Downarowicz and Zhang8, Theorem 7.5]). We include the full construction here for the sake of completeness and because we leverage our control over the foremost system
![]() $T_0$
, which is not explicitly referenced in the constructions found in [Reference Downarowicz and Zhang8, Reference Downarowicz and Zhang9].
$T_0$
, which is not explicitly referenced in the constructions found in [Reference Downarowicz and Zhang8, Reference Downarowicz and Zhang9].
In principle, we wish to embed all the information of an arbitrary point
![]() $x\in X$
into a point
$x\in X$
into a point
![]() $y\in Y$
injectively and continuously (that is, in such a way that it can be uniquely and ‘locally’ decoded). From x, we derive quasi-tilings
$y\in Y$
injectively and continuously (that is, in such a way that it can be uniquely and ‘locally’ decoded). From x, we derive quasi-tilings
![]() $t_0$
,
$t_0$
,
![]() $t_1$
, and
$t_1$
, and
![]() $t_2$
as above. On the side of X, the fact that
$t_2$
as above. On the side of X, the fact that
![]() $t_2$
is exact (and therefore covers G) allows us to partition all of the information in x into local ‘blocks’ of a bounded size. The fact that
$t_2$
is exact (and therefore covers G) allows us to partition all of the information in x into local ‘blocks’ of a bounded size. The fact that
![]() $t_2$
covers G is especially significant for our construction; it would be fine if
$t_2$
covers G is especially significant for our construction; it would be fine if
![]() $t_2$
was not perfectly disjoint, so long as we had full covering and only a small (controllable) amount of ‘redundancy’. Then, by choosing our quasi-tilings with shapes sufficiently large, we may exhibit an injective map from patterns of shapes from
$t_2$
was not perfectly disjoint, so long as we had full covering and only a small (controllable) amount of ‘redundancy’. Then, by choosing our quasi-tilings with shapes sufficiently large, we may exhibit an injective map from patterns of shapes from
![]() $T_2$
in X to patterns of shapes from
$T_2$
in X to patterns of shapes from
![]() $T_1$
in Y (we describe this as a ‘block injection’). Here we invoke the hypothesis
$T_1$
in Y (we describe this as a ‘block injection’). Here we invoke the hypothesis
![]() $h(X) < h(Y)$
, as well as the fact that each shape from
$h(X) < h(Y)$
, as well as the fact that each shape from
![]() $T_2$
is only slightly (controllably) larger in cardinality than a shape from
$T_2$
is only slightly (controllably) larger in cardinality than a shape from
![]() $T_1$
, as careful estimation shows. We thereby construct a point of Y by taking blocks from x, passing them through block injections to obtain blocks of Y, and gluing them together within Y via a mixing condition. On this side, we see that the fact that
$T_1$
, as careful estimation shows. We thereby construct a point of Y by taking blocks from x, passing them through block injections to obtain blocks of Y, and gluing them together within Y via a mixing condition. On this side, we see that the fact that
![]() $t_1$
is disjoint is essential, so that there are no conflicts in laying these blocks together within Y. It is permissible for
$t_1$
is disjoint is essential, so that there are no conflicts in laying these blocks together within Y. It is permissible for
![]() $t_1$
to not completely cover G, which is indeed the situation we grapple with in the coming proof.
$t_1$
to not completely cover G, which is indeed the situation we grapple with in the coming proof.
That leaves open the issue of how to decode the point x if only given y. If one knew which tilings
![]() $t_1$
and
$t_1$
and
![]() $t_2$
were used to construct y from x, then it would be easy: simply look at the patterns appearing in y on each of the tiles of
$t_2$
were used to construct y from x, then it would be easy: simply look at the patterns appearing in y on each of the tiles of
![]() $t_1$
, pass these backwards through the block injections described above, then lay these new blocks upon the tiles of
$t_1$
, pass these backwards through the block injections described above, then lay these new blocks upon the tiles of
![]() $t_2$
and thereby reconstruct x. Here we use the quasi-tiling
$t_2$
and thereby reconstruct x. Here we use the quasi-tiling
![]() $t_0$
, which has a controlled number of shapes and tile centers spread arbitrarily sparsely throughout the group. This forces the ‘information density’ of
$t_0$
, which has a controlled number of shapes and tile centers spread arbitrarily sparsely throughout the group. This forces the ‘information density’ of
![]() $t_0$
to be arbitrarily low, and hence we are able to encode
$t_0$
to be arbitrarily low, and hence we are able to encode
![]() $t_0$
within y (with the use of marker patterns) by giving up only a subset of symbols of controllably small density.
$t_0$
within y (with the use of marker patterns) by giving up only a subset of symbols of controllably small density.
Given y, one is therefore able to decode the point
![]() $t_0$
by looking at the marker patterns, thereby deriving both
$t_0$
by looking at the marker patterns, thereby deriving both
![]() $t_1$
and
$t_1$
and
![]() $t_2$
, thereby decoding x by the algorithm outlined above.
$t_2$
, thereby decoding x by the algorithm outlined above.
Theorem 3.5. Let G be a countable amenable group with the comparison property. Let X be a non-empty strongly aperiodic subshift over G. Let Y be a strongly irreducible SFT over G with no global period. If
![]() $h(X) < h(Y)$
and Y contains at least one factor of X, then X embeds into Y.
$h(X) < h(Y)$
and Y contains at least one factor of X, then X embeds into Y.
Proof. Let
![]() ${\mathcal A}_X$
and
${\mathcal A}_X$
and
![]() ${\mathcal A}_Y$
be finite alphabets such that
${\mathcal A}_Y$
be finite alphabets such that
![]() $X\subset {\mathcal A}_X^G$
and
$X\subset {\mathcal A}_X^G$
and
![]() $Y\subset {\mathcal A}_Y^G$
. Suppose
$Y\subset {\mathcal A}_Y^G$
. Suppose
![]() ${\phi : X \to Y}$
is a homomorphism, not necessarily injective, in which case
${\phi : X \to Y}$
is a homomorphism, not necessarily injective, in which case
![]() $\tilde {Y} = \phi (X) \subset Y$
is a factor of X. Note that
$\tilde {Y} = \phi (X) \subset Y$
is a factor of X. Note that
![]() $h(\tilde {Y}) \leq h(X) < h(Y)$
. Without loss of generality (by Lemma 3.1), we may assume that Y separates elements of G (Definition 3.1). In that case, by Theorem 3.2, there exists a strongly irreducible subshift
$h(\tilde {Y}) \leq h(X) < h(Y)$
. Without loss of generality (by Lemma 3.1), we may assume that Y separates elements of G (Definition 3.1). In that case, by Theorem 3.2, there exists a strongly irreducible subshift
![]() $Y_0$
that separates elements of G and satisfies
$Y_0$
that separates elements of G and satisfies
![]() $\tilde {Y} \subset Y_0 \subset Y$
and
$\tilde {Y} \subset Y_0 \subset Y$
and
![]() $h(X) < h(Y_0) < h(Y)$
. By [Reference Bland, McGoff and Pavlov2, Theorem 4.2], there exists an SFT
$h(X) < h(Y_0) < h(Y)$
. By [Reference Bland, McGoff and Pavlov2, Theorem 4.2], there exists an SFT
![]() $Y_1$
such that
$Y_1$
such that
![]() $Y_0 \subset Y_1 \subset Y$
and
$Y_0 \subset Y_1 \subset Y$
and
![]() $h(Y_1) < h(Y)$
. It is significant for our proof that these inequalities are strict.
$h(Y_1) < h(Y)$
. It is significant for our proof that these inequalities are strict.
Choose a finite subset
![]() $K \subset G$
with
$K \subset G$
with
![]() $e\in K$
such that
$e\in K$
such that
![]() $K^{-1} = K$
, K witnesses Y and
$K^{-1} = K$
, K witnesses Y and
![]() $Y_1$
as SFTs, and K witnesses Y and
$Y_1$
as SFTs, and K witnesses Y and
![]() $Y_0$
as strongly irreducible. As in the proof of Theorem 3.2, we shall abbreviate
$Y_0$
as strongly irreducible. As in the proof of Theorem 3.2, we shall abbreviate
![]() $\operatorname {\mathrm {int}}^n F = \operatorname {\mathrm {int}}_{K^n} F$
and
$\operatorname {\mathrm {int}}^n F = \operatorname {\mathrm {int}}_{K^n} F$
and
![]() $\partial ^n F = \partial _{K^n} F = F \setminus \operatorname {\mathrm {int}}^n F$
for each natural
$\partial ^n F = \partial _{K^n} F = F \setminus \operatorname {\mathrm {int}}^n F$
for each natural
![]() $n \in \mathbb {N}$
and finite subset
$n \in \mathbb {N}$
and finite subset
![]() $F \subset G$
for the remainder of this proof. We shall also abbreviate
$F \subset G$
for the remainder of this proof. We shall also abbreviate
![]() $\partial ^n p = p(\partial ^n F)$
for each pattern p of shape F.
$\partial ^n p = p(\partial ^n F)$
for each pattern p of shape F.
Choose
![]() $\varepsilon> 0$
such that
$\varepsilon> 0$
such that
![]() $\varepsilon < 1/3$
and
$\varepsilon < 1/3$
and
Choose
![]() $r = 1 + \lceil (2/\varepsilon )\log (1/\varepsilon )\rceil $
, in which case,
$r = 1 + \lceil (2/\varepsilon )\log (1/\varepsilon )\rceil $
, in which case,
![]() $(1-\varepsilon /2)^r < \varepsilon $
. Let
$(1-\varepsilon /2)^r < \varepsilon $
. Let
![]() $M \subset G$
be the subset delivered by Theorem 3.4 for
$M \subset G$
be the subset delivered by Theorem 3.4 for
![]() $Y_0$
,
$Y_0$
,
![]() $Y_1$
, Y, and r as chosen here. By passing to a superset of M if necessary, we may assume that
$Y_1$
, Y, and r as chosen here. By passing to a superset of M if necessary, we may assume that
![]() $K \subset M$
and that
$K \subset M$
and that
![]() $M^{-1} = M$
. Choose a finite subset
$M^{-1} = M$
. Choose a finite subset
![]() $L \subset G$
such that
$L \subset G$
such that
![]() $M^6 \subset L$
and
$M^6 \subset L$
and
![]() $|M^6|/|L| < \varepsilon $
.
$|M^6|/|L| < \varepsilon $
.
Let
![]() $T_0 \subset \Lambda ({\mathcal S}_0)^G$
be the quasi-tiling system delivered by Theorem 2.9 for X,
$T_0 \subset \Lambda ({\mathcal S}_0)^G$
be the quasi-tiling system delivered by Theorem 2.9 for X,
![]() $\varepsilon $
, r, and L as chosen here, with
$\varepsilon $
, r, and L as chosen here, with
![]() $n_0$
chosen so that every
$n_0$
chosen so that every
![]() $S_0 \in {\mathcal S}_0$
satisfies the following hypotheses.
$S_0 \in {\mathcal S}_0$
satisfies the following hypotheses.
-
(H1)
 $1/|S_0| < \varepsilon (1-\varepsilon )$
.
$1/|S_0| < \varepsilon (1-\varepsilon )$
. -
(H2)
 $(|K^3||M^6||L|)|LS_0 \setminus S_0| < \varepsilon |S_0|$
.
$(|K^3||M^6||L|)|LS_0 \setminus S_0| < \varepsilon |S_0|$
. -
(H3)
 $h(S_0, X) < h(X) + \varepsilon $
.
$h(S_0, X) < h(X) + \varepsilon $
.
Note that Theorem 2.9 gives that
![]() $|{\mathcal S}_0| \leq r$
, so choose and fix an enumeration
$|{\mathcal S}_0| \leq r$
, so choose and fix an enumeration
![]() $(S_0^{(i)})_{i}$
of
$(S_0^{(i)})_{i}$
of
![]() ${\mathcal S}_0$
where
${\mathcal S}_0$
where
![]() $i = 1, \ldots , r$
. Theorem 2.9 also gives that every quasi-tiling
$i = 1, \ldots , r$
. Theorem 2.9 also gives that every quasi-tiling
![]() $t_0 \in T_0$
is
$t_0 \in T_0$
is
![]() $\varepsilon $
-disjoint, as witnessed by a continuous and shift-commuting retraction map
$\varepsilon $
-disjoint, as witnessed by a continuous and shift-commuting retraction map
![]() $t_0 \mapsto \operatorname {\mathrm {ret}}(t_0)$
. Let
$t_0 \mapsto \operatorname {\mathrm {ret}}(t_0)$
. Let
![]() ${\mathcal S}_1$
be the set of all shapes realized as tiles of
${\mathcal S}_1$
be the set of all shapes realized as tiles of
![]() $\operatorname {\mathrm {ret}}(t_0)$
for each
$\operatorname {\mathrm {ret}}(t_0)$
for each
![]() $t_0 \in T_0$
. Each shape
$t_0 \in T_0$
. Each shape
![]() $S_0 \in {\mathcal S}_0$
gives rise to a subcollection of shapes
$S_0 \in {\mathcal S}_0$
gives rise to a subcollection of shapes
![]() $S_1 \in {\mathcal S}_1$
, all of which satisfy
$S_1 \in {\mathcal S}_1$
, all of which satisfy
![]() $S_1 \subset S_0$
and
$S_1 \subset S_0$
and
![]() $|S_0 \setminus S_1| < \varepsilon |S_0|$
. Let
$|S_0 \setminus S_1| < \varepsilon |S_0|$
. Let
![]() $T_1 = \operatorname {\mathrm {ret}}(T_0) \subset \Lambda ({\mathcal S}_1)^G$
be the system of all quasi-tilings obtained by taking retractions of the quasi-tilings in
$T_1 = \operatorname {\mathrm {ret}}(T_0) \subset \Lambda ({\mathcal S}_1)^G$
be the system of all quasi-tilings obtained by taking retractions of the quasi-tilings in
![]() $T_0$
, in which case the map
$T_0$
, in which case the map
![]() $\operatorname {\mathrm {ret}}$
is a factor map from
$\operatorname {\mathrm {ret}}$
is a factor map from
![]() $T_0$
to
$T_0$
to
![]() $T_1$
. Note that every
$T_1$
. Note that every
![]() $t_1 \in T_1$
is disjoint by Theorem 2.9. Moreover, every
$t_1 \in T_1$
is disjoint by Theorem 2.9. Moreover, every
![]() $t_1 \in T_1$
is
$t_1 \in T_1$
is
![]() $(1-\varepsilon )$
-covering, since the retraction map
$(1-\varepsilon )$
-covering, since the retraction map
![]() $\operatorname {\mathrm {ret}}$
has the property that
$\operatorname {\mathrm {ret}}$
has the property that
![]() $\bigcup _g t_0(g)g = \bigcup _g \operatorname {\mathrm {ret}}(t_0)(g)g$
for each
$\bigcup _g t_0(g)g = \bigcup _g \operatorname {\mathrm {ret}}(t_0)(g)g$
for each
![]() $t_0 \in T_0$
, and every
$t_0 \in T_0$
, and every
![]() $t_0 \in T_0$
is
$t_0 \in T_0$
is
![]() $(1-\varepsilon )$
-covering by Theorem 2.9.
$(1-\varepsilon )$
-covering by Theorem 2.9.
We aim to go one step further and construct a factor
![]() $T_2$
of
$T_2$
of
![]() $T_1$
, which shall be a system of exact tilings. It is in this step that we appeal to the comparison property of G. To begin, note that for each pair of shapes
$T_1$
, which shall be a system of exact tilings. It is in this step that we appeal to the comparison property of G. To begin, note that for each pair of shapes
![]() $S_0 \in {\mathcal S}_0$
and
$S_0 \in {\mathcal S}_0$
and
![]() $S_1 \in {\mathcal S}_1$
with
$S_1 \in {\mathcal S}_1$
with
![]() $S_1 \subset S_0$
and
$S_1 \subset S_0$
and
![]() $|S_0 \setminus S_1| < \varepsilon |S_0|$
, it holds that
$|S_0 \setminus S_1| < \varepsilon |S_0|$
, it holds that
where above we invoke hypothesis (H1). This implies that there exists an integer in the interval
![]() $[2\varepsilon |S_1|, 3\varepsilon |S_1|)$
. Therefore, for each shape
$[2\varepsilon |S_1|, 3\varepsilon |S_1|)$
. Therefore, for each shape
![]() $S_1 \in {\mathcal S}_1$
, we may find and fix an arbitrary subset
$S_1 \in {\mathcal S}_1$
, we may find and fix an arbitrary subset
![]() $B(S_1) \subset S_1$
such that
$B(S_1) \subset S_1$
such that
![]() $2\varepsilon |S_1| \leq |B(S_1)| < 3\varepsilon |S_1|$
.
$2\varepsilon |S_1| \leq |B(S_1)| < 3\varepsilon |S_1|$
.
To each
![]() $t_1 \in T_1$
, we assign two disjoint subsets
$t_1 \in T_1$
, we assign two disjoint subsets
![]() $A_{t_1}$
,
$A_{t_1}$
,
![]() $B_{t_1}$
of G in the following way. Let
$B_{t_1}$
of G in the following way. Let
![]() $A_{t_1} = G \setminus \bigcup _g {t_1}(g)g$
and let
$A_{t_1} = G \setminus \bigcup _g {t_1}(g)g$
and let
![]() $B_{t_1} = \bigcup _g B({t_1}(g))g$
. Observe that the assignments
$B_{t_1} = \bigcup _g B({t_1}(g))g$
. Observe that the assignments
![]() ${{t_1} \mapsto A_{t_1}}$
,
${{t_1} \mapsto A_{t_1}}$
,
![]() $B_{t_1}$
are continuous and shift-commuting. Observe also that
$B_{t_1}$
are continuous and shift-commuting. Observe also that
![]() $\overline {D}(A_{t_1}) \leq \varepsilon $
because
$\overline {D}(A_{t_1}) \leq \varepsilon $
because
![]() ${t_1}$
is
${t_1}$
is
![]() $(1-\varepsilon )$
-covering, and that
$(1-\varepsilon )$
-covering, and that
![]() $\underline {D}(B_{t_1}) \geq 2\varepsilon (1-\varepsilon )$
by Lemma 2.8 (with
$\underline {D}(B_{t_1}) \geq 2\varepsilon (1-\varepsilon )$
by Lemma 2.8 (with
![]() $\rho _0 = 1-\varepsilon $
and
$\rho _0 = 1-\varepsilon $
and
![]() $\rho _1 = 2\varepsilon $
). Consequently,
$\rho _1 = 2\varepsilon $
). Consequently,
where above we have used the fact that
![]() $\varepsilon \in (0,1/2)$
.
$\varepsilon \in (0,1/2)$
.
Therefore, by Theorem 2.10, there exists a family of injections
![]() $\phi _{t_1} : A_{t_1} \to B_{t_1}$
that is induced by a block code, in the sense that there is a finite subset
$\phi _{t_1} : A_{t_1} \to B_{t_1}$
that is induced by a block code, in the sense that there is a finite subset
![]() $F \subset G$
and a function
$F \subset G$
and a function
![]() $\Phi : {\mathcal P}(F, T_1) \to F$
such that for every
$\Phi : {\mathcal P}(F, T_1) \to F$
such that for every
![]() $t_1\in T_1$
and
$t_1\in T_1$
and
![]() $g\in A_{t_1}$
, it holds that
$g\in A_{t_1}$
, it holds that
With this, we are ready to construct
![]() $T_2$
. For each
$T_2$
. For each
![]() $t_1 \in T_1$
, let
$t_1 \in T_1$
, let
![]() $t_2 = \operatorname {\mathrm {ex}}(t_1)$
be the quasi-tiling obtained according to the rule
$t_2 = \operatorname {\mathrm {ex}}(t_1)$
be the quasi-tiling obtained according to the rule
for every
![]() $c \in C(t_1)$
, and
$c \in C(t_1)$
, and
![]() $t_2(g) = \varnothing $
otherwise. In words, we expand each tile
$t_2(g) = \varnothing $
otherwise. In words, we expand each tile
![]() $t_1(c)c$
by including all group elements that map into
$t_1(c)c$
by including all group elements that map into
![]() $B(t_1(c))c \subset B_{t_1}$
under the injective map
$B(t_1(c))c \subset B_{t_1}$
under the injective map
![]() $\phi _{t_1}$
. Consequently,
$\phi _{t_1}$
. Consequently,
![]() $|t_2(c) \setminus t_1(c)| \leq |B(t_1(c))| < 3\varepsilon |t_1(c)|$
for every
$|t_2(c) \setminus t_1(c)| \leq |B(t_1(c))| < 3\varepsilon |t_1(c)|$
for every
![]() $c \in C(t_2) = C(t_1)$
.
$c \in C(t_2) = C(t_1)$
.
Let
![]() ${\mathcal S}_2$
be the set of all shapes realized as tiles of
${\mathcal S}_2$
be the set of all shapes realized as tiles of
![]() $\operatorname {\mathrm {ex}}(t_1)$
for each
$\operatorname {\mathrm {ex}}(t_1)$
for each
![]() $t_1 \in T_1$
. There are at most finitely many because
$t_1 \in T_1$
. There are at most finitely many because
![]() $\operatorname {\mathrm {ex}}(t_1)(g) \subset F^{-1}t_1(g)$
for every
$\operatorname {\mathrm {ex}}(t_1)(g) \subset F^{-1}t_1(g)$
for every
![]() $g\in G$
. Each shape
$g\in G$
. Each shape
![]() $S_1 \in {\mathcal S}_1$
gives rise to a subcollection of shapes
$S_1 \in {\mathcal S}_1$
gives rise to a subcollection of shapes
![]() $S_2 \in {\mathcal S}_2$
, all of which satisfy
$S_2 \in {\mathcal S}_2$
, all of which satisfy
![]() $S_1 \subset S_2$
and
$S_1 \subset S_2$
and
![]() $|S_2 \setminus S_1|< 3\varepsilon |S_1|$
.
$|S_2 \setminus S_1|< 3\varepsilon |S_1|$
.
Let
![]() $T_2 = \operatorname {\mathrm {ex}}(T_1) \subset \Lambda ({\mathcal S}_2)^G$
. We claim that the map
$T_2 = \operatorname {\mathrm {ex}}(T_1) \subset \Lambda ({\mathcal S}_2)^G$
. We claim that the map
![]() $\operatorname {\mathrm {ex}}$
is a homomorphism and that every
$\operatorname {\mathrm {ex}}$
is a homomorphism and that every
![]() $t_2 \in T_2$
is an exact tiling of G. To see that the map
$t_2 \in T_2$
is an exact tiling of G. To see that the map
![]() $\operatorname {\mathrm {ex}}$
is continuous and shift-commuting, let
$\operatorname {\mathrm {ex}}$
is continuous and shift-commuting, let
![]() $t_1 \in T_1$
be arbitrary and let
$t_1 \in T_1$
be arbitrary and let
![]() $t_2 = \operatorname {\mathrm {ex}}(t_1)$
. We note that for each
$t_2 = \operatorname {\mathrm {ex}}(t_1)$
. We note that for each
![]() $g \in G$
and
$g \in G$
and
![]() $c \in C(t_2) = C(t_1)$
, the definition given above implies that
$c \in C(t_2) = C(t_1)$
, the definition given above implies that
![]() $g\in t_2(c)$
if and only if
$g\in t_2(c)$
if and only if
Moreover, for each
![]() $f \in F$
, we have
$f \in F$
, we have
![]() $\sigma ^{gc}(t_1)(f) = t_1(fgc) = \sigma ^c(t_1)(fg)$
. Because
$\sigma ^{gc}(t_1)(f) = t_1(fgc) = \sigma ^c(t_1)(fg)$
. Because
![]() $t_2(c) \subset F^{-1}t_1(c)$
, we see that
$t_2(c) \subset F^{-1}t_1(c)$
, we see that
![]() $t_2(c)$
depends only on
$t_2(c)$
depends only on
![]() $\sigma ^c(t_1)(FF^{-1}U_1)$
, where
$\sigma ^c(t_1)(FF^{-1}U_1)$
, where
![]() $U_1 = \bigcup _{S_1\in {\mathcal S}_1} S_1$
. This demonstrates that the map
$U_1 = \bigcup _{S_1\in {\mathcal S}_1} S_1$
. This demonstrates that the map
![]() $\operatorname {\mathrm {ex}}$
is induced by a block code, which is sufficient to demonstrate that
$\operatorname {\mathrm {ex}}$
is induced by a block code, which is sufficient to demonstrate that
![]() $\operatorname {\mathrm {ex}}$
is continuous and shift-commuting.
$\operatorname {\mathrm {ex}}$
is continuous and shift-commuting.
For the claimed exactness, let
![]() $t_2 \in T_2$
and
$t_2 \in T_2$
and
![]() $g\in G$
be arbitrary. Choose
$g\in G$
be arbitrary. Choose
![]() $t_1 \in T_1$
such that
$t_1 \in T_1$
such that
![]() $t_2 = \operatorname {\mathrm {ex}}(t_1)$
. If there exists a
$t_2 = \operatorname {\mathrm {ex}}(t_1)$
. If there exists a
![]() $c \in C(t_1)$
such that
$c \in C(t_1)$
such that
![]() $g\in t_1(c)c$
, then the c is necessarily unique by the disjointness of
$g\in t_1(c)c$
, then the c is necessarily unique by the disjointness of
![]() $t_1$
and also it follows that
$t_1$
and also it follows that
![]() $g \in t_2(c)c$
. Otherwise,
$g \in t_2(c)c$
. Otherwise,
![]() $g\in A_{t_1}$
, in which case
$g\in A_{t_1}$
, in which case
![]() $\phi _{t_1}(g) \in B_{t_1} = \bigcup _c B(t_1(c))c$
. Therefore, there exists a
$\phi _{t_1}(g) \in B_{t_1} = \bigcup _c B(t_1(c))c$
. Therefore, there exists a
![]() $c \in C(t_1)$
such that
$c \in C(t_1)$
such that
![]() $\phi _{t_1}(g)\in B(t_1(c))c \subset t_1(c)c$
. The c must again be unique by the disjointness of
$\phi _{t_1}(g)\in B(t_1(c))c \subset t_1(c)c$
. The c must again be unique by the disjointness of
![]() $t_1$
. Then
$t_1$
. Then
![]() $g\in \phi _{t_1}^{-1}(B(t_1(c)c)) \subset t_2(c)c$
. We see that for each
$g\in \phi _{t_1}^{-1}(B(t_1(c)c)) \subset t_2(c)c$
. We see that for each
![]() $g\in G$
, there exists a unique
$g\in G$
, there exists a unique
![]() $c \in C(t_2)$
such that
$c \in C(t_2)$
such that
![]() $g\in t_2(c)c$
, and hence
$g\in t_2(c)c$
, and hence
![]() $t_2$
is an exact tiling of G.
$t_2$
is an exact tiling of G.
There is one last quasi-tiling system we shall need. Let
![]() ${\mathcal S}_1^{*}$
denote the collection of all shapes obtained in the form
${\mathcal S}_1^{*}$
denote the collection of all shapes obtained in the form
![]() $\operatorname {\mathrm {int}}^3(S_1 \setminus M^6C)$
for any
$\operatorname {\mathrm {int}}^3(S_1 \setminus M^6C)$
for any
![]() $S_1 \in {\mathcal S}_1$
and any L-separated subset
$S_1 \in {\mathcal S}_1$
and any L-separated subset
![]() $C\subset G$
. Each shape
$C\subset G$
. Each shape
![]() $S_1 \in {\mathcal S}_1$
gives rise to a subcollection of shapes
$S_1 \in {\mathcal S}_1$
gives rise to a subcollection of shapes
![]() $S_1^{*} \in {\mathcal S}_1^{*}$
, all of which satisfy
$S_1^{*} \in {\mathcal S}_1^{*}$
, all of which satisfy
![]() $S_1^{*} \subset S_1$
. For each
$S_1^{*} \subset S_1$
. For each
![]() $t_1 \in T_1$
, let
$t_1 \in T_1$
, let
![]() $t_1^{*}$
be the retraction of
$t_1^{*}$
be the retraction of
![]() $t_1$
such that, for each
$t_1$
such that, for each
![]() $c\in C(t_1)$
, it holds that
$c\in C(t_1)$
, it holds that
and
![]() $t_1^{*}(g) = \varnothing $
otherwise. Observe that each such quasi-tiling belongs to
$t_1^{*}(g) = \varnothing $
otherwise. Observe that each such quasi-tiling belongs to
![]() $\Lambda (S_1^{*})^G$
. Let
$\Lambda (S_1^{*})^G$
. Let
![]() $T_1^{*} = \{t_1^{*} \in \Lambda ({\mathcal S}_1^{*})^G : t_1 \in T_1\}$
. It is quick to see that the map
$T_1^{*} = \{t_1^{*} \in \Lambda ({\mathcal S}_1^{*})^G : t_1 \in T_1\}$
. It is quick to see that the map
![]() $t_1 \mapsto t_1^{*}$
is a factor map from
$t_1 \mapsto t_1^{*}$
is a factor map from
![]() $T_1$
to
$T_1$
to
![]() $T_1^{*}$
, because the assignment
$T_1^{*}$
, because the assignment
![]() $t_1 \mapsto C(t_1)$
is continuous and shift-commuting. Moreover, for any choice of
$t_1 \mapsto C(t_1)$
is continuous and shift-commuting. Moreover, for any choice of
![]() $t_0 \in T_0$
with corresponding
$t_0 \in T_0$
with corresponding
![]() $t_1$
,
$t_1$
,
![]() $t_2$
, and
$t_2$
, and
![]() $t_1^{*}$
, it holds that
$t_1^{*}$
, it holds that
![]() $C(t_0) = C(t_1) = C(t_2) = C(t_1^{*})$
, thus all of these subsets are L-separated.
$C(t_0) = C(t_1) = C(t_2) = C(t_1^{*})$
, thus all of these subsets are L-separated.
With our quasi-tiling systems constructed, we now aim to construct an injection that will carry patterns on tiles in X to patterns on tiles in
![]() $Y_0$
. On the side of X, we use patterns of those shapes belonging to
$Y_0$
. On the side of X, we use patterns of those shapes belonging to
![]() ${\mathcal S}_2$
. On the side of
${\mathcal S}_2$
. On the side of
![]() $Y_0$
, we shall use patterns of those shapes belonging to
$Y_0$
, we shall use patterns of those shapes belonging to
![]() ${\mathcal S}_1^{*}$
. We separate out the construction (and its rather involved estimations) into the following lemma.
${\mathcal S}_1^{*}$
. We separate out the construction (and its rather involved estimations) into the following lemma.
Lemma 3.6. Let
![]() $(S_0, S_1, S_2, S_1^{*})$
be any tuple of shapes from
$(S_0, S_1, S_2, S_1^{*})$
be any tuple of shapes from
![]() ${\mathcal S}_0$
,
${\mathcal S}_0$
,
![]() ${\mathcal S}_1$
,
${\mathcal S}_1$
,
![]() ${\mathcal S}_2$
, and
${\mathcal S}_2$
, and
![]() ${\mathcal S}_1^{*}$
, respectively, such that
${\mathcal S}_1^{*}$
, respectively, such that
![]() $S_1^{*} \subset S_1 \subset S_0 \cap S_2$
,
$S_1^{*} \subset S_1 \subset S_0 \cap S_2$
,
![]() $|S_0 \setminus S_1| < \varepsilon |S_0|$
,
$|S_0 \setminus S_1| < \varepsilon |S_0|$
,
![]() $|S_2 \setminus S_1| < 3\varepsilon |S_1|$
, and
$|S_2 \setminus S_1| < 3\varepsilon |S_1|$
, and
![]() ${S_1^{*} = \operatorname {\mathrm {int}}^3(S_1 \setminus M^6C)}$
for some L-separated subset
${S_1^{*} = \operatorname {\mathrm {int}}^3(S_1 \setminus M^6C)}$
for some L-separated subset
![]() $C\subset G$
. Then
$C\subset G$
. Then
Proof. We begin on the side of X. By the hypotheses, a quick calculation shows that
![]() $|S_0 \triangle S_2| < 5\varepsilon |S_0|$
. It therefore holds that
$|S_0 \triangle S_2| < 5\varepsilon |S_0|$
. It therefore holds that
where above we invoke hypothesis (H3) in the latter inequality.
Now we shall estimate the number of patterns in
![]() $Y_0$
of shape
$Y_0$
of shape
![]() $S_1^{*}$
. We begin by estimating the size of
$S_1^{*}$
. We begin by estimating the size of
![]() $S_1^{*}$
in terms of the size of
$S_1^{*}$
in terms of the size of
![]() $S_0$
. We proceed in stages, beginning with
$S_0$
. We proceed in stages, beginning with
![]() $S_1$
. We first note that
$S_1$
. We first note that
 $$ \begin{align*} |S_1 \cap M^6C| & \leq |S_0 \cap M^6C|\\ &\leq \frac{|M^6|}{|L|}|S_0| + |M^6||\partial_L S_0| + |M^6||(M^6)^{-1}S_0 \setminus S_0|\\ &< \varepsilon|S_0| + \varepsilon|S_0| + \varepsilon|S_0|\\ & = 3\varepsilon|S_0|, \end{align*} $$
$$ \begin{align*} |S_1 \cap M^6C| & \leq |S_0 \cap M^6C|\\ &\leq \frac{|M^6|}{|L|}|S_0| + |M^6||\partial_L S_0| + |M^6||(M^6)^{-1}S_0 \setminus S_0|\\ &< \varepsilon|S_0| + \varepsilon|S_0| + \varepsilon|S_0|\\ & = 3\varepsilon|S_0|, \end{align*} $$
where above we have used the fact that
![]() $S_1 \subset S_0$
, Lemma 2.4, the choice of L, Lemma 2.3, and hypothesis (H2) in conjunction with the fact that
$S_1 \subset S_0$
, Lemma 2.4, the choice of L, Lemma 2.3, and hypothesis (H2) in conjunction with the fact that
![]() $(M^6)^{-1} = M^6 \subset L$
. It follows that
$(M^6)^{-1} = M^6 \subset L$
. It follows that
This, together with the fact that
![]() $S_1 \setminus M^6C \subset S_1 \subset S_0$
, gives us
$S_1 \setminus M^6C \subset S_1 \subset S_0$
, gives us
 $$ \begin{align*} |\partial^3(S_1 \setminus M^6C)| &\leq |K^3||K^3(S_1 \setminus M^6C) \setminus (S_1\setminus M^6C)|\\ &\leq |K^3||K^3S_0 \setminus S_0| + |K^3|^2|S_0 \setminus(S_1 \setminus M^6C)|\\ &< \varepsilon|S_0| + |K|^6 \cdot 4\varepsilon|S_0|\\ &= \varepsilon(1 + 4|K|^6)|S_0|, \end{align*} $$
$$ \begin{align*} |\partial^3(S_1 \setminus M^6C)| &\leq |K^3||K^3(S_1 \setminus M^6C) \setminus (S_1\setminus M^6C)|\\ &\leq |K^3||K^3S_0 \setminus S_0| + |K^3|^2|S_0 \setminus(S_1 \setminus M^6C)|\\ &< \varepsilon|S_0| + |K|^6 \cdot 4\varepsilon|S_0|\\ &= \varepsilon(1 + 4|K|^6)|S_0|, \end{align*} $$
where above we have used Lemmas 2.3, 2.1, hypothesis (H2) in conjunction with the fact that
![]() $K^3 \subset L$
, and the calculation of the previous display.
$K^3 \subset L$
, and the calculation of the previous display.
The combination of the previous two displays gives us
 $$ \begin{align*} |\!\operatorname{\mathrm{int}}^3(S_1 \setminus M^6C)| &= |S_1 \setminus M^6C| - |\partial^3(S_1 \setminus M^6C)| \\ & \geq (1-4\varepsilon)|S_0| - \varepsilon(1+4|K|^6)|S_0| \\ &= |S_0| - \varepsilon(5+4|K|^6)|S_0|. \end{align*} $$
$$ \begin{align*} |\!\operatorname{\mathrm{int}}^3(S_1 \setminus M^6C)| &= |S_1 \setminus M^6C| - |\partial^3(S_1 \setminus M^6C)| \\ & \geq (1-4\varepsilon)|S_0| - \varepsilon(1+4|K|^6)|S_0| \\ &= |S_0| - \varepsilon(5+4|K|^6)|S_0|. \end{align*} $$
Recall that
![]() $S_1^{*} = \operatorname {\mathrm {int}}^3(S_1 \setminus M^6C)$
and note that
$S_1^{*} = \operatorname {\mathrm {int}}^3(S_1 \setminus M^6C)$
and note that
![]() $|{\mathcal P}(S_0, Y_0)| \leq |{\mathcal P}(S_1^{*}, Y_0)| \cdot |{\mathcal A}_Y|^{|S_0 \setminus S_1^{*}|}$
. This, in combination with the previous display, gives that
$|{\mathcal P}(S_0, Y_0)| \leq |{\mathcal P}(S_1^{*}, Y_0)| \cdot |{\mathcal A}_Y|^{|S_0 \setminus S_1^{*}|}$
. This, in combination with the previous display, gives that
 $$ \begin{align*} |{\mathcal P}(S_1^{*}, Y_0)| &\geq |{\mathcal P}(S_0, Y_0)| \cdot |{\mathcal A}_Y|^{-|S_0 \setminus S_1^{*}|}\\ &> e^{h(Y_0)|S_0|} \cdot |{\mathcal A}_Y|^{-\varepsilon(5+4|K|^6)|S_0|}, \end{align*} $$
$$ \begin{align*} |{\mathcal P}(S_1^{*}, Y_0)| &\geq |{\mathcal P}(S_0, Y_0)| \cdot |{\mathcal A}_Y|^{-|S_0 \setminus S_1^{*}|}\\ &> e^{h(Y_0)|S_0|} \cdot |{\mathcal A}_Y|^{-\varepsilon(5+4|K|^6)|S_0|}, \end{align*} $$
where above we have also used the fact that
![]() $h(S_0,Y_0) \geq h(Y_0)$
(see Definition 2.11). Our choice of
$h(S_0,Y_0) \geq h(Y_0)$
(see Definition 2.11). Our choice of
![]() $\varepsilon $
gives us
$\varepsilon $
gives us
in which case the previous calculation, in combination with (X1), finally gives that
The previous lemma implies that for each tuple
![]() $(S_0, S_1, S_2, S_1^{*})$
satisfying the hypotheses of the previous lemma, there exists an injective map
$(S_0, S_1, S_2, S_1^{*})$
satisfying the hypotheses of the previous lemma, there exists an injective map
Let these injections be chosen and fixed. We now continue the proof of Theorem 3.5.
Here we choose our marker patterns. Pick a point
![]() $y^{(m)} \in Y_0$
arbitrarily to serve as the ‘substrate’ of the marker patterns. Let
$y^{(m)} \in Y_0$
arbitrarily to serve as the ‘substrate’ of the marker patterns. Let
![]() $y_1,\ldots , y_r \in Y$
and
$y_1,\ldots , y_r \in Y$
and
![]() $m_i = y_i(M) \in {\mathcal P}(M,Y)\setminus {\mathcal P}(M,Y_1)$
be the points and patterns delivered by Theorem 3.4 for the choice of substrate
$m_i = y_i(M) \in {\mathcal P}(M,Y)\setminus {\mathcal P}(M,Y_1)$
be the points and patterns delivered by Theorem 3.4 for the choice of substrate
![]() $y^{(m)}$
.
$y^{(m)}$
.
Now we appeal to the strong irreducibility of
![]() $Y_0$
to construct certain ‘mixing’ patterns. We do this twice: once for patterns of shape
$Y_0$
to construct certain ‘mixing’ patterns. We do this twice: once for patterns of shape
![]() $M^6$
, and once for patterns of each shape
$M^6$
, and once for patterns of each shape
![]() $S_1^{*}\in {\mathcal S}_1^{*}$
.
$S_1^{*}\in {\mathcal S}_1^{*}$
.
Note that
![]() $K^2\cdot KM^3 \subset M^6$
because
$K^2\cdot KM^3 \subset M^6$
because
![]() $K\subset M$
, thus
$K\subset M$
, thus
![]() $KM^3 \subset \operatorname {\mathrm {int}}^2(M^6)$
and thus
$KM^3 \subset \operatorname {\mathrm {int}}^2(M^6)$
and thus
![]() $KM^3$
is disjoint from
$KM^3$
is disjoint from
![]() $\partial ^2M^6$
. The subshift
$\partial ^2M^6$
. The subshift
![]() $Y_0$
is strongly irreducible as witnessed by K; therefore, for any pair of patterns
$Y_0$
is strongly irreducible as witnessed by K; therefore, for any pair of patterns
![]() $u\in {\mathcal P}(M^3, Y_0)$
and
$u\in {\mathcal P}(M^3, Y_0)$
and
![]() $\partial ^2 v \in {\mathcal P}(\partial ^2M^6, Y_0)$
, there is a pattern
$\partial ^2 v \in {\mathcal P}(\partial ^2M^6, Y_0)$
, there is a pattern
![]() $w\in {\mathcal P}(M^6,Y_0)$
such that
$w\in {\mathcal P}(M^6,Y_0)$
such that
![]() $w(g) = u(g)$
for each
$w(g) = u(g)$
for each
![]() $g\in M^3$
and
$g\in M^3$
and
![]() $w(g) = \partial ^2v(g)$
for each
$w(g) = \partial ^2v(g)$
for each
![]() $g\in \partial ^2M^6$
. Choose and fix one such pattern w for each choice of u and
$g\in \partial ^2M^6$
. Choose and fix one such pattern w for each choice of u and
![]() $\partial ^2v$
; we shall denote it by
$\partial ^2v$
; we shall denote it by
![]() $w = u\cup \partial ^2 v$
.
$w = u\cup \partial ^2 v$
.
Let
![]() $S_1^{*} \in {\mathcal S}_1^{*}$
be arbitrary and suppose
$S_1^{*} \in {\mathcal S}_1^{*}$
be arbitrary and suppose
![]() $S_1^{*} = \operatorname {\mathrm {int}}^3(S_1 \setminus M^6C)$
for some shape
$S_1^{*} = \operatorname {\mathrm {int}}^3(S_1 \setminus M^6C)$
for some shape
![]() $S_1 \in {\mathcal S}_1$
and some L-separated subset
$S_1 \in {\mathcal S}_1$
and some L-separated subset
![]() $C \subset G$
. Observe that
$C \subset G$
. Observe that
![]() $K^2\cdot KS_1^{*} \subset S_1\setminus M^6C$
, and thus
$K^2\cdot KS_1^{*} \subset S_1\setminus M^6C$
, and thus
![]() $KS_1^{*}$
is disjoint from
$KS_1^{*}$
is disjoint from
![]() $\partial ^2(S_1\setminus M^6C)$
. Therefore, for each pair of patterns
$\partial ^2(S_1\setminus M^6C)$
. Therefore, for each pair of patterns
![]() $u\in {\mathcal P}(S_1^{*}, Y_0)$
and
$u\in {\mathcal P}(S_1^{*}, Y_0)$
and
![]() $\partial ^2 v\in {\mathcal P}(\partial ^2(S_1\setminus M^6C), Y_0)$
, there is a pattern
$\partial ^2 v\in {\mathcal P}(\partial ^2(S_1\setminus M^6C), Y_0)$
, there is a pattern
![]() $w \in {\mathcal P}(S_1\setminus M^6C, Y_0)$
such that
$w \in {\mathcal P}(S_1\setminus M^6C, Y_0)$
such that
![]() ${w(g) = u(g)}$
for each
${w(g) = u(g)}$
for each
![]() $g \in S_1^{*}$
and
$g \in S_1^{*}$
and
![]() $w(g) = \partial ^2v(g)$
for each
$w(g) = \partial ^2v(g)$
for each
![]() $g\in \partial ^2(S_1\setminus M^6C)$
. Choose and fix one such pattern w for each choice of u and
$g\in \partial ^2(S_1\setminus M^6C)$
. Choose and fix one such pattern w for each choice of u and
![]() $\partial ^2v$
; we shall again denote it by
$\partial ^2v$
; we shall again denote it by
![]() $w = u \cup \partial ^2 v$
.
$w = u \cup \partial ^2 v$
.
We are now ready to construct the map
![]() $\psi : X \to Y$
desired for the theorem. To begin, let
$\psi : X \to Y$
desired for the theorem. To begin, let
![]() $x\in X$
be fixed, let
$x\in X$
be fixed, let
![]() $t_0 = {\mathcal T}(x)\in T_0$
, let
$t_0 = {\mathcal T}(x)\in T_0$
, let
![]() $t_1 = \operatorname {\mathrm {ret}}(t_0) \in T_1$
, let
$t_1 = \operatorname {\mathrm {ret}}(t_0) \in T_1$
, let
![]() $t_2 = \operatorname {\mathrm {ex}}(t_1) \in T_2$
, let
$t_2 = \operatorname {\mathrm {ex}}(t_1) \in T_2$
, let
![]() $t_1^{*} \in T_1^{*}$
be delivered by
$t_1^{*} \in T_1^{*}$
be delivered by
![]() $t_1$
, and let
$t_1$
, and let
![]() $y_0 = \phi (x)\in Y_0$
be the point delivered by the homomorphism
$y_0 = \phi (x)\in Y_0$
be the point delivered by the homomorphism
![]() $\phi : X \to Y$
assumed to exist at the beginning of the proof. Let
$\phi : X \to Y$
assumed to exist at the beginning of the proof. Let
![]() $C = C(t_0) = C(t_1) = C(t_2) = C(t_1^{*}) \subset G$
.
$C = C(t_0) = C(t_1) = C(t_2) = C(t_1^{*}) \subset G$
.
We construct the point
![]() $y = \psi (x)\in Y$
in two stages, first by constructing a point
$y = \psi (x)\in Y$
in two stages, first by constructing a point
![]() $y_1 \in Y_1$
that locally looks like a point of
$y_1 \in Y_1$
that locally looks like a point of
![]() $Y_0$
, and then modifying
$Y_0$
, and then modifying
![]() $y_1$
into a point of Y by placing down the marker patterns.
$y_1$
into a point of Y by placing down the marker patterns.
Note that for each
![]() $c \in C$
, the tuple of shapes
$c \in C$
, the tuple of shapes
![]() $(t_0(c), t_1(c), t_2(c), t_1^{*}(c))$
satisfies the hypotheses of Lemma 3.6 by construction. Let
$(t_0(c), t_1(c), t_2(c), t_1^{*}(c))$
satisfies the hypotheses of Lemma 3.6 by construction. Let
![]() $y_1$
be the point satisfying the following two conditions for every
$y_1$
be the point satisfying the following two conditions for every
![]() $c\in C$
when
$c\in C$
when
![]() $(S_1, S_2, S_1^{*}) = (t_1(c), t_2(c), t_1^{*}(c))$
:
$(S_1, S_2, S_1^{*}) = (t_1(c), t_2(c), t_1^{*}(c))$
:
Everywhere else, let
![]() $y_1(g) = y_0(g)$
. Here we use the block injection(s)
$y_1(g) = y_0(g)$
. Here we use the block injection(s)
![]() $\Psi (S_2,S_1^{*})$
delivered by Lemma 3.6, as well as the mixing boundary patterns
$\Psi (S_2,S_1^{*})$
delivered by Lemma 3.6, as well as the mixing boundary patterns
![]() $w = u\cup \partial ^2 v$
constructed earlier. The construction of
$w = u\cup \partial ^2 v$
constructed earlier. The construction of
![]() $y_1$
is illustrated in Figure 2.
$y_1$
is illustrated in Figure 2.

Figure 2 An illustration of the construction of
![]() $y_1$
for a hypothetical tiling of
$y_1$
for a hypothetical tiling of
![]() $\mathbb {Z}^2$
using different sized circles. The largest solid circles indicate the tiles of
$\mathbb {Z}^2$
using different sized circles. The largest solid circles indicate the tiles of
![]() $t_0$
(the overlap, indicated by dashed lines, is removed in
$t_0$
(the overlap, indicated by dashed lines, is removed in
![]() $t_1$
). The smaller solid circles indicate the translates of
$t_1$
). The smaller solid circles indicate the translates of
![]() $M^6$
, wherein the marker patterns will later be placed. The stippled tile interiors are the patterns given by the block injections from Lemma 3.6. The darkened boundaries are delivered by the strong irreducibility of
$M^6$
, wherein the marker patterns will later be placed. The stippled tile interiors are the patterns given by the block injections from Lemma 3.6. The darkened boundaries are delivered by the strong irreducibility of
![]() $Y_0$
, to mix each tile interior pattern with its respective boundary pattern from
$Y_0$
, to mix each tile interior pattern with its respective boundary pattern from
![]() $y_0$
. The small hatched circles are each labeled with the pattern drawn from the marker substrate,
$y_0$
. The small hatched circles are each labeled with the pattern drawn from the marker substrate,
![]() $y^{(m)}(M^3)$
. The shaded exterior is the base point
$y^{(m)}(M^3)$
. The shaded exterior is the base point
![]() $y_0$
.
$y_0$
.
First we argue that
![]() $y_1$
is well defined. Let
$y_1$
is well defined. Let
![]() $g\in G$
be fixed; we split over three cases. If
$g\in G$
be fixed; we split over three cases. If
![]() $g\in M^6C$
, then there is a unique
$g\in M^6C$
, then there is a unique
![]() $c \in C$
such that
$c \in C$
such that
![]() $g\in M^6c$
because C is L-separated and
$g\in M^6c$
because C is L-separated and
![]() $M^6 \subset L$
. In this case,
$M^6 \subset L$
. In this case,
![]() $y_1(g)$
is determined by the condition in equation (C1). If
$y_1(g)$
is determined by the condition in equation (C1). If
![]() $g\in (\bigcup _c t_1(c)c)\setminus M^6C$
, then again there is a unique
$g\in (\bigcup _c t_1(c)c)\setminus M^6C$
, then again there is a unique
![]() $c\in C$
such that
$c\in C$
such that
![]() $g\in t_1(c)c\setminus M^6C = (t_1(c)\setminus M^6Cc^{-1})c$
by the disjointness of
$g\in t_1(c)c\setminus M^6C = (t_1(c)\setminus M^6Cc^{-1})c$
by the disjointness of
![]() $t_1$
. In this case,
$t_1$
. In this case,
![]() $y_1(g)$
is determined by the condition in equation (C2). Otherwise,
$y_1(g)$
is determined by the condition in equation (C2). Otherwise,
![]() $y_1(g) = y_0(g)$
is again uniquely determined.
$y_1(g) = y_0(g)$
is again uniquely determined.
Next we argue that
![]() $y_1$
belongs to
$y_1$
belongs to
![]() $Y_1$
. Recall that
$Y_1$
. Recall that
![]() $Y_1$
is an SFT as witnessed by K. Let
$Y_1$
is an SFT as witnessed by K. Let
![]() $g\in G$
be arbitrary and consider the translate
$g\in G$
be arbitrary and consider the translate
![]() $Kg$
. If
$Kg$
. If
![]() $Kg$
intersects
$Kg$
intersects
![]() $\operatorname {\mathrm {int}}^2(M^6)c$
for some
$\operatorname {\mathrm {int}}^2(M^6)c$
for some
![]() $c\in C$
, then
$c\in C$
, then
![]() $Kg \subset M^6c$
by Lemma 2.2 and the fact that
$Kg \subset M^6c$
by Lemma 2.2 and the fact that
![]() $K = K^{-1}$
. Moreover, the c must be unique. In this case,
$K = K^{-1}$
. Moreover, the c must be unique. In this case,
![]() $\sigma ^g(y_1)(K)$
is given by the condition in equation (C1) and therefore
$\sigma ^g(y_1)(K)$
is given by the condition in equation (C1) and therefore
![]() $\sigma ^g(y_1)(K) \in {\mathcal P}(K,Y_0)$
. If
$\sigma ^g(y_1)(K) \in {\mathcal P}(K,Y_0)$
. If
![]() $Kg$
intersects
$Kg$
intersects
![]() $\operatorname {\mathrm {int}}^2(t_1(c)c \setminus M^6C)$
for some
$\operatorname {\mathrm {int}}^2(t_1(c)c \setminus M^6C)$
for some
![]() $c\in C$
, then
$c\in C$
, then
![]() $Kg \subset t_1(c)c \setminus M^6C$
also by Lemma 2.2, in which case the c must again be unique. In this case,
$Kg \subset t_1(c)c \setminus M^6C$
also by Lemma 2.2, in which case the c must again be unique. In this case,
![]() $\sigma ^g(y_1)(K)$
is given by the condition in equation (C2) and therefore
$\sigma ^g(y_1)(K)$
is given by the condition in equation (C2) and therefore
![]() $\sigma ^g(y_1)(K) \in {\mathcal P}(K,Y_0)$
again. If neither of these cases hold, then
$\sigma ^g(y_1)(K) \in {\mathcal P}(K,Y_0)$
again. If neither of these cases hold, then
 $$ \begin{align*} Kg \subset (G \setminus M^6 C) \cup \partial^2(M^6)C \cup \bigg(G \setminus \bigcup_c (t_1(c)c \setminus M^6C)\bigg) \cup \bigcup_c \partial^2(t_1(c)c \setminus M^6C). \end{align*} $$
$$ \begin{align*} Kg \subset (G \setminus M^6 C) \cup \partial^2(M^6)C \cup \bigg(G \setminus \bigcup_c (t_1(c)c \setminus M^6C)\bigg) \cup \bigcup_c \partial^2(t_1(c)c \setminus M^6C). \end{align*} $$
In this case,
![]() $\sigma ^g(y_1)(K) = \sigma ^g(y_0)(K)$
and therefore
$\sigma ^g(y_1)(K) = \sigma ^g(y_0)(K)$
and therefore
![]() $\sigma ^g(y_1)(K) \in {\mathcal P}(K,Y_0)$
again. We see that every pattern of shape K appearing in
$\sigma ^g(y_1)(K) \in {\mathcal P}(K,Y_0)$
again. We see that every pattern of shape K appearing in
![]() $y_1$
is allowed in
$y_1$
is allowed in
![]() $Y_0$
. Since
$Y_0$
. Since
![]() $Y_0 \subset Y_1$
and
$Y_0 \subset Y_1$
and
![]() $Y_1$
is an SFT witnessed by K, we conclude that
$Y_1$
is an SFT witnessed by K, we conclude that
![]() $y_1 \in Y_1$
.
$y_1 \in Y_1$
.
Next we argue that the map
![]() $x\mapsto y_1$
is continuous and shift-commuting. For a fixed
$x\mapsto y_1$
is continuous and shift-commuting. For a fixed
![]() $g \in G$
, to determine the symbol
$g \in G$
, to determine the symbol
![]() $y_1(g)$
, one must know first the tiles from
$y_1(g)$
, one must know first the tiles from
![]() $t_0$
,
$t_0$
,
![]() $t_1$
,
$t_1$
,
![]() $t_2$
, and
$t_2$
, and
![]() $t_1^{*}$
to which g belongs. This requires looking only at the symbols of the involved quasi-tilings within a finite neighborhood of g. Then, one either applies the condition in equation (C1) or the condition in equation (C2) or returns
$t_1^{*}$
to which g belongs. This requires looking only at the symbols of the involved quasi-tilings within a finite neighborhood of g. Then, one either applies the condition in equation (C1) or the condition in equation (C2) or returns
![]() $y_0(g)$
. As every involved quasi-tiling and
$y_0(g)$
. As every involved quasi-tiling and
![]() $y_0$
are derived from x in a continuous and shift-commuting manner, it is evident that
$y_0$
are derived from x in a continuous and shift-commuting manner, it is evident that
![]() $y_1(g)$
depends only on
$y_1(g)$
depends only on
![]() $\sigma ^g(x)(F_1)$
, where
$\sigma ^g(x)(F_1)$
, where
![]() $F_1$
is some (possibly very large but) finite subset of G. We conclude that the map
$F_1$
is some (possibly very large but) finite subset of G. We conclude that the map
![]() $x \mapsto y_1$
is continuous and shift-commuting (but possibly non-injective).
$x \mapsto y_1$
is continuous and shift-commuting (but possibly non-injective).
Finally, we construct
![]() $y = \psi (x) \in Y$
from
$y = \psi (x) \in Y$
from
![]() $y_1$
as follows. For every
$y_1$
as follows. For every
![]() $c\in C$
, let y satisfy
$c\in C$
, let y satisfy
![]() $\sigma ^c(y)(M) = m_i$
, where
$\sigma ^c(y)(M) = m_i$
, where
![]() $i\in [1,r]$
is the index of the shape
$i\in [1,r]$
is the index of the shape
![]() $t_0(c) = S_0^{(i)} \in {\mathcal S}_0$
that was fixed at the beginning of the proof, and
$t_0(c) = S_0^{(i)} \in {\mathcal S}_0$
that was fixed at the beginning of the proof, and
![]() $m_i$
is the corresponding marker pattern. Everywhere else, let
$m_i$
is the corresponding marker pattern. Everywhere else, let
![]() $y(g) = y_1(g)$
. The construction of y near a tile center is illustrated in Figure 3.
$y(g) = y_1(g)$
. The construction of y near a tile center is illustrated in Figure 3.

Figure 3 An illustration of the construction of y near a tile center. The marker pattern
![]() $m_i$
corresponding to the shape
$m_i$
corresponding to the shape
![]() $S_0^{(i)}$
is placed directly over the marker substrate, the pattern
$S_0^{(i)}$
is placed directly over the marker substrate, the pattern
![]() $y^{(m)}(M^3)$
.
$y^{(m)}(M^3)$
.
The point y is well defined by identical argument as (and as a consequence of) the fact that
![]() $y_1$
is well defined. Before proceeding, we note a property of y that is critical to later arguments. Let
$y_1$
is well defined. Before proceeding, we note a property of y that is critical to later arguments. Let
![]() $c\in C$
be arbitrary and suppose that
$c\in C$
be arbitrary and suppose that
![]() $t_0(c) = S_0^{(i)}$
for some unique index
$t_0(c) = S_0^{(i)}$
for some unique index
![]() $i \in [1,r]$
. Recall
$i \in [1,r]$
. Recall
![]() $y_i \in Y$
is the point from which the marker pattern
$y_i \in Y$
is the point from which the marker pattern
![]() $m_i$
is drawn. Then
$m_i$
is drawn. Then
This is true because
![]() $\sigma ^c(y)(M) = m_i = y_i(M)$
by construction, together with the fact that
$\sigma ^c(y)(M) = m_i = y_i(M)$
by construction, together with the fact that
where above we have used the construction of y, the condition in equation (C2), and Theorem 3.4.
Next we argue that y belongs to Y. Recall that Y is an SFT witnessed by K. Let
![]() $g\in G$
be arbitrary and consider the translate
$g\in G$
be arbitrary and consider the translate
![]() $Kg$
. If
$Kg$
. If
![]() $Kg$
intersects
$Kg$
intersects
![]() $Mc$
for some
$Mc$
for some
![]() $c\in C$
, then
$c\in C$
, then
![]() $Kg\subset M^3c$
by the fact that
$Kg\subset M^3c$
by the fact that
![]() $K = K^{-1}$
and
$K = K^{-1}$
and
![]() $K\subset M$
. Moreover, the c must be unique. Then, if
$K\subset M$
. Moreover, the c must be unique. Then, if
![]() $t_0(c) = S_0^{(i)}$
for some unique index
$t_0(c) = S_0^{(i)}$
for some unique index
![]() $i\in [1,r]$
, property (Y1) implies that
$i\in [1,r]$
, property (Y1) implies that
![]() $\sigma ^g(y)(K) = \sigma ^{gc^{-1}}(y_i)(K)$
. As
$\sigma ^g(y)(K) = \sigma ^{gc^{-1}}(y_i)(K)$
. As
![]() $y_i \in Y$
, we therefore see that
$y_i \in Y$
, we therefore see that
![]() $\sigma ^g(y)(K) \in {\mathcal P}(K,Y)$
. In the opposite case,
$\sigma ^g(y)(K) \in {\mathcal P}(K,Y)$
. In the opposite case,
![]() $Kg \subset G\setminus MC$
, in which case
$Kg \subset G\setminus MC$
, in which case
![]() $\sigma ^g(y)(K) = \sigma ^g(y_1)(K)$
by construction. Because
$\sigma ^g(y)(K) = \sigma ^g(y_1)(K)$
by construction. Because
![]() $y_1 \in Y_1 \subset Y$
, we again see that
$y_1 \in Y_1 \subset Y$
, we again see that
![]() $\sigma ^g(y)(K) \in {\mathcal P}(K,Y)$
. Therefore, every pattern of shape K appearing in y is allowed in Y, and thus
$\sigma ^g(y)(K) \in {\mathcal P}(K,Y)$
. Therefore, every pattern of shape K appearing in y is allowed in Y, and thus
![]() $y\in Y$
.
$y\in Y$
.
Next we argue that the map
![]() $\psi $
is continuous and shift-commuting. This follows by identical argument as (and as a consequence of) the fact that the map
$\psi $
is continuous and shift-commuting. This follows by identical argument as (and as a consequence of) the fact that the map
![]() $x \mapsto y_1$
is continuous and shift-commuting.
$x \mapsto y_1$
is continuous and shift-commuting.
Before proving that the map
![]() $\psi $
is injective, we note one more property in advance. Let
$\psi $
is injective, we note one more property in advance. Let
![]() $x\in X$
be fixed, let
$x\in X$
be fixed, let
![]() $t_0 = {\mathcal T}(x)\in T_0$
, let
$t_0 = {\mathcal T}(x)\in T_0$
, let
![]() $C = C(t_0) \subset G$
, and let
$C = C(t_0) \subset G$
, and let
![]() $y = \psi (x) \in Y$
. We claim that for each
$y = \psi (x) \in Y$
. We claim that for each
![]() $g\in G$
and each index
$g\in G$
and each index
![]() $i\in [1,r]$
, we have
$i\in [1,r]$
, we have
The reverse implication is obvious by construction. For the forward implication, let
![]() $g\in G$
be arbitrary and suppose
$g\in G$
be arbitrary and suppose
![]() $\sigma ^g(y)(M) = m_i$
for some index
$\sigma ^g(y)(M) = m_i$
for some index
![]() $i\in [1,r]$
. If
$i\in [1,r]$
. If
![]() $Mg$
is disjoint from
$Mg$
is disjoint from
![]() $MC$
, then
$MC$
, then
![]() $\sigma ^g(y)(M) = \sigma ^g(y_1)(M)$
, in which case
$\sigma ^g(y)(M) = \sigma ^g(y_1)(M)$
, in which case
![]() $\sigma ^g(y)(M) = m_i$
contradicts the fact that
$\sigma ^g(y)(M) = m_i$
contradicts the fact that
![]() $m_i$
is forbidden in
$m_i$
is forbidden in
![]() $Y_1$
. Therefore,
$Y_1$
. Therefore,
![]() $Mg$
must intersect
$Mg$
must intersect
![]() $MC$
, in which case
$MC$
, in which case
![]() $Mg \subset M^3c$
for some
$Mg \subset M^3c$
for some
![]() $c\in C$
by the fact that
$c\in C$
by the fact that
![]() $M = M^{-1}$
. Moreover, the c must be unique; indeed, if
$M = M^{-1}$
. Moreover, the c must be unique; indeed, if
![]() ${Mg \subset M^3c_1}$
and
${Mg \subset M^3c_1}$
and
![]() $Mg\subset M^3c_2$
for distinct
$Mg\subset M^3c_2$
for distinct
![]() $c_1\neq c_2$
, then
$c_1\neq c_2$
, then
![]() $g\in M^4c_1 \cap M^4c_2 \neq \varnothing $
, contradicting the fact that C is L-separated and
$g\in M^4c_1 \cap M^4c_2 \neq \varnothing $
, contradicting the fact that C is L-separated and
![]() $M^4 \subset L$
. Then suppose
$M^4 \subset L$
. Then suppose
![]() $t_0(c) = S_0^{(j)}$
for some index
$t_0(c) = S_0^{(j)}$
for some index
![]() $j\in [1,r]$
. By property (Y1), we have that
$j\in [1,r]$
. By property (Y1), we have that
![]() $\sigma ^c(y)(M^3) = y_j(M^3)$
. Moreover, the fact that
$\sigma ^c(y)(M^3) = y_j(M^3)$
. Moreover, the fact that
![]() $\sigma ^g(y)(M) = m_i$
implies that
$\sigma ^g(y)(M) = m_i$
implies that
![]() $m_i = \sigma ^{gc^{-1}}(y_j)(M)$
. By Theorem 3.4, this only happens in the case where
$m_i = \sigma ^{gc^{-1}}(y_j)(M)$
. By Theorem 3.4, this only happens in the case where
![]() $j = i$
and
$j = i$
and
![]() $g = c$
. The claim follows.
$g = c$
. The claim follows.
Finally, we argue that
![]() $\psi $
is injective. Let
$\psi $
is injective. Let
![]() $x_1$
,
$x_1$
,
![]() $x_2\in X$
be arbitrary and suppose that
$x_2\in X$
be arbitrary and suppose that
![]() $\psi (x_1) = \psi (x_2)$
. Property (Y2) implies that
$\psi (x_1) = \psi (x_2)$
. Property (Y2) implies that
![]() ${\mathcal T}(x_1) = {\mathcal T}(x_2) = t_0 \in T_0$
. Then, let
${\mathcal T}(x_1) = {\mathcal T}(x_2) = t_0 \in T_0$
. Then, let
![]() $t_1$
,
$t_1$
,
![]() $t_1^{*}$
, and
$t_1^{*}$
, and
![]() $t_2$
be derived from
$t_2$
be derived from
![]() $t_0$
as before and let
$t_0$
as before and let
![]() $C = C(t_0) \subset G$
. The condition in equation (C2) and the fact that
$C = C(t_0) \subset G$
. The condition in equation (C2) and the fact that
![]() $\Psi $
is an injective map implies that
$\Psi $
is an injective map implies that
![]() $\sigma ^c(x_1)(t_2(c)) = \sigma ^c(x_2)(t_2(c))$
for every
$\sigma ^c(x_1)(t_2(c)) = \sigma ^c(x_2)(t_2(c))$
for every
![]() $c\in C$
. Because
$c\in C$
. Because
![]() $t_2$
is an exact tiling of G, it follows that
$t_2$
is an exact tiling of G, it follows that
![]() $x_1 = x_2$
.
$x_1 = x_2$
.
4. Discussion
In Theorem 3.5, can the assumption that Y contains a factor of X be dropped? That is, under what conditions on X and Y does there necessarily exist a homomorphism
![]() $\phi : X \to Y$
? This is true if for example Y contains a fixed point, because every subshift factors onto a fixed point. A homomorphism was constructed by Lightwood [Reference Lightwood15, Theorem 2.8] for
$\phi : X \to Y$
? This is true if for example Y contains a fixed point, because every subshift factors onto a fixed point. A homomorphism was constructed by Lightwood [Reference Lightwood15, Theorem 2.8] for
![]() ${G = \mathbb {Z}^2}$
in the case that X is strongly aperiodic and Y is an SFT that satisfies the ‘square-filling mixing’ condition, therefore providing an extension of Krieger’s embedding theorem to
${G = \mathbb {Z}^2}$
in the case that X is strongly aperiodic and Y is an SFT that satisfies the ‘square-filling mixing’ condition, therefore providing an extension of Krieger’s embedding theorem to
![]() $\mathbb {Z}^2$
. However, the existence of such homomorphisms in general remains open, even for
$\mathbb {Z}^2$
. However, the existence of such homomorphisms in general remains open, even for
![]() $G = \mathbb {Z}^d$
where
$G = \mathbb {Z}^d$
where
![]() $d\geq 3$
.
$d\geq 3$
.
Can the mixing condition on Y be weakened? One might wish to replace the ‘uniform’ mixing condition of strong irreducibility with a non-uniform mixing condition, such as topological mixing. However, such conditions are too weak for the construction given here, as we rely on the fact that we can cut and paste patterns on tiles in Y that are ‘packed together’ relatively tightly, with the tiling known to cover a fraction of the group which can be chosen arbitrarily close to
![]() $1$
. Furthermore, it is known that topological mixing is too weak for a general embedding theorem (that is, for a general X) even for
$1$
. Furthermore, it is known that topological mixing is too weak for a general embedding theorem (that is, for a general X) even for
![]() $G = \mathbb {Z}^2$
; indeed, Quas and Şahin [Reference Quas and Şahin19, Theorem 1.1] have constructed an example of a topologically mixing SFT Y and a non-negative constant
$G = \mathbb {Z}^2$
; indeed, Quas and Şahin [Reference Quas and Şahin19, Theorem 1.1] have constructed an example of a topologically mixing SFT Y and a non-negative constant
![]() $h_0 < h(Y)$
such that if X is any subshift with the uniform filling property (a mixing condition stronger than topological mixing) which satisfies
$h_0 < h(Y)$
such that if X is any subshift with the uniform filling property (a mixing condition stronger than topological mixing) which satisfies
![]() $h_0 \leq h(X) \leq h(Y)$
, then X cannot be embedded in Y.
$h_0 \leq h(X) \leq h(Y)$
, then X cannot be embedded in Y.
Can the assumption that G has the comparison property be dropped? If there are no amenable groups without the comparison property, then this point is moot. We invoke the comparison property in two places in this proof, in each case to construct a desirable system of quasi-tilings. In the first case, as part of the construction of the subshift
![]() $Y_0$
, we construct a strongly irreducible system of exact tilings of G by way of Theorem 2.11 (due to Downarowicz and Zhang [Reference Downarowicz and Zhang8, Reference Downarowicz and Zhang9]) in combination with a construction of Frisch and Tamuz [Reference Frisch and Tamuz10]. In the second case, we adapt the proof of Theorem 2.11 to construct a system
$Y_0$
, we construct a strongly irreducible system of exact tilings of G by way of Theorem 2.11 (due to Downarowicz and Zhang [Reference Downarowicz and Zhang8, Reference Downarowicz and Zhang9]) in combination with a construction of Frisch and Tamuz [Reference Frisch and Tamuz10]. In the second case, we adapt the proof of Theorem 2.11 to construct a system
![]() $T_2$
of exact tilings as a factor of a suitable system of disjoint quasi-tilings
$T_2$
of exact tilings as a factor of a suitable system of disjoint quasi-tilings
![]() $T_1$
. As mentioned before, the most significant aspect of
$T_1$
. As mentioned before, the most significant aspect of
![]() $T_2$
is that its tilings completely cover G, and disjointness here could in principle be traded for near-disjointness.
$T_2$
is that its tilings completely cover G, and disjointness here could in principle be traded for near-disjointness.
If one refuses the comparison property and uses instead either
![]() $T_0$
or
$T_0$
or
![]() $T_1$
on the side of X to construct the map
$T_1$
on the side of X to construct the map
![]() $\psi : X \to Y$
, then
$\psi : X \to Y$
, then
![]() $\psi $
has the property that for every
$\psi $
has the property that for every
![]() $x_1$
,
$x_1$
,
![]() ${x_2\in X}$
, if
${x_2\in X}$
, if
![]() $\psi (x_1) = \psi (x_2)$
, then
$\psi (x_1) = \psi (x_2)$
, then
![]() ${\mathcal T}(x_1) = {\mathcal T}(x_2) = t_0\in T_0$
and
${\mathcal T}(x_1) = {\mathcal T}(x_2) = t_0\in T_0$
and
![]() $x_1(g) = x_2(g)$
for every
$x_1(g) = x_2(g)$
for every
![]() ${g\in \bigcup _c t_0(c)c}$
. This map is therefore not necessarily injective (unless
${g\in \bigcup _c t_0(c)c}$
. This map is therefore not necessarily injective (unless
![]() $t_0$
covers G), but one does have that the difference in entropy between X and
$t_0$
covers G), but one does have that the difference in entropy between X and
![]() $\psi (X) \subset Y$
can be made arbitrarily small (based on the covering density of
$\psi (X) \subset Y$
can be made arbitrarily small (based on the covering density of
![]() $t_0$
). Therefore, in this case, if Y contains at least one factor of X, then necessarily Y contains many ‘non-trivial’ factors of X, in particular with entropy arbitrarily close to X.
$t_0$
). Therefore, in this case, if Y contains at least one factor of X, then necessarily Y contains many ‘non-trivial’ factors of X, in particular with entropy arbitrarily close to X.
One aspect of the quasi-tilings given by Theorem 2.9 that we have not exploited is that they are actually maximal, in the sense that no one additional tile of any shape could be inserted anywhere without breaking the
![]() $\varepsilon $
-disjointness property (this is seen if one closely inspects the proof of [Reference Downarowicz and Huczek6, Lemma 3.4]). This condition is similar to that of the
$\varepsilon $
-disjointness property (this is seen if one closely inspects the proof of [Reference Downarowicz and Huczek6, Lemma 3.4]). This condition is similar to that of the
![]() $\rho $
-covering condition (Definition 2.16); while the
$\rho $
-covering condition (Definition 2.16); while the
![]() $\rho $
-covering is only in general witnessed at some ‘scale’ F (depending on the quasi-tiling, and possibly much larger than the tiles themselves), the maximality implies that the covering is somehow witnessed on the scale of the tiles. This leverage could be useful for some applications.
$\rho $
-covering is only in general witnessed at some ‘scale’ F (depending on the quasi-tiling, and possibly much larger than the tiles themselves), the maximality implies that the covering is somehow witnessed on the scale of the tiles. This leverage could be useful for some applications.
Acknowledgements
This work is part of the author’s PhD dissertation, conducted under the guidance of Kevin McGoff. The author would also like to thank Mike Boyle, as well as the anonymous reviewer, whose many helpful comments significantly improved the exposition of this paper. This work was supported in part by the National Science Foundation grant DMS-1847144.