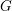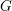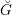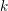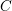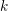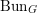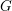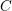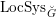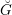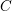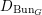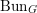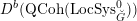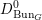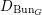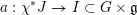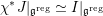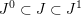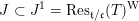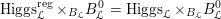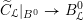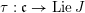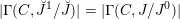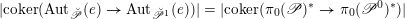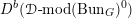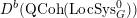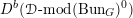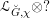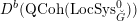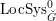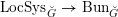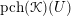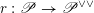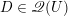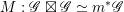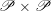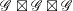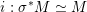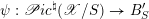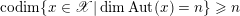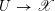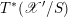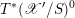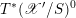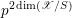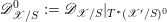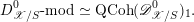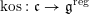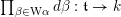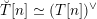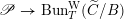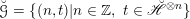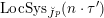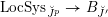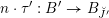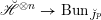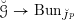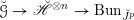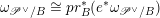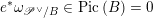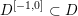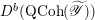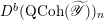1 Introduction
1.1 Geometric Langlands conjecture in prime characteristic
Let
![]() $G$
be a reductive algebraic group over
$G$
be a reductive algebraic group over
![]() $\mathbb{C}$
and let
$\mathbb{C}$
and let
![]() $\breve{G}$
be its Langlands dual group. Let
$\breve{G}$
be its Langlands dual group. Let
![]() $C$
be a smooth projective curve over
$C$
be a smooth projective curve over
![]() $\mathbb{C}$
. Let
$\mathbb{C}$
. Let
![]() $\operatorname{Bun}_{G}$
be the stack of
$\operatorname{Bun}_{G}$
be the stack of
![]() $G$
-bundles on
$G$
-bundles on
![]() $C$
and
$C$
and
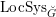 $\operatorname{LocSys}_{\breve{G}}$
be the stack of de Rham
$\operatorname{LocSys}_{\breve{G}}$
be the stack of de Rham
![]() $\breve{G}$
-local systems on
$\breve{G}$
-local systems on
![]() $C$
. The geometric Langlands conjecture (GLC), as proposed by Beilinson and Drinfeld, is a conjectural equivalence between certain appropriately defined category of quasi-coherent sheaves on
$C$
. The geometric Langlands conjecture (GLC), as proposed by Beilinson and Drinfeld, is a conjectural equivalence between certain appropriately defined category of quasi-coherent sheaves on
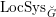 $\operatorname{LocSys}_{\breve{G}}$
and certain appropriately defined category of
$\operatorname{LocSys}_{\breve{G}}$
and certain appropriately defined category of
![]() ${\mathcal{D}}$
-modules on
${\mathcal{D}}$
-modules on
![]() $\operatorname{Bun}_{G}$
. A precise formulation of this conjecture (over
$\operatorname{Bun}_{G}$
. A precise formulation of this conjecture (over
![]() $\mathbb{C}$
) can be found in the recent work of Arinkin and Gaitsgory [Reference Arinkin and GaitsgoryAG12, Reference GaitsgoryGai13].
$\mathbb{C}$
) can be found in the recent work of Arinkin and Gaitsgory [Reference Arinkin and GaitsgoryAG12, Reference GaitsgoryGai13].
The geometric Langlands duality has a classical limit which amounts to the duality of Hitchin fibrations. The classical duality is established ‘generically’ by Donagi and Pantev in [Reference Donagi and PantevDP12] over
![]() $\mathbb{C}$
.
$\mathbb{C}$
.
In this paper, we establish a ‘generic’ characteristic
![]() $p$
version of the geometric Langlands conjecture. Namely, let
$p$
version of the geometric Langlands conjecture. Namely, let
![]() $G$
be a semi-simple algebraic group over an algebraically closed field
$G$
be a semi-simple algebraic group over an algebraically closed field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p$
that does not divide the order of the Weyl group of
$p$
that does not divide the order of the Weyl group of
![]() $G$
, and let
$G$
, and let
![]() $\breve{G}$
be its Langlands dual group, defined over
$\breve{G}$
be its Langlands dual group, defined over
![]() $k$
. Let
$k$
. Let
![]() $C$
be a smooth projective curve over
$C$
be a smooth projective curve over
![]() $k$
of genus at least two.Footnote
1
Then we establish an equivalence of bounded derived category
$k$
of genus at least two.Footnote
1
Then we establish an equivalence of bounded derived category
 $$\begin{eqnarray}D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})^{0})\simeq D^{b}(\operatorname{QCoh}(\operatorname{LocSys}_{\breve{G}})^{0}),\end{eqnarray}$$
$$\begin{eqnarray}D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})^{0})\simeq D^{b}(\operatorname{QCoh}(\operatorname{LocSys}_{\breve{G}})^{0}),\end{eqnarray}$$
where
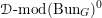 ${\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})^{0}$
(respectively
${\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})^{0}$
(respectively
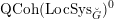 $\operatorname{QCoh}(\operatorname{LocSys}_{\breve{G}})^{0}$
) is a certain localization of the category of
$\operatorname{QCoh}(\operatorname{LocSys}_{\breve{G}})^{0}$
) is a certain localization of the category of
![]() ${\mathcal{D}}$
-modules on
${\mathcal{D}}$
-modules on
![]() $\operatorname{Bun}_{G}$
(respectively a localization of the category of quasi-coherent sheaves on
$\operatorname{Bun}_{G}$
(respectively a localization of the category of quasi-coherent sheaves on
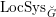 $\operatorname{LocSys}_{\breve{G}}$
). We call (1.1.1) a ‘generic’ version of the GLC.
$\operatorname{LocSys}_{\breve{G}}$
). We call (1.1.1) a ‘generic’ version of the GLC.
One remark is in order. Recall that over a field of positive characteristic, there are different objects that can be called
![]() ${\mathcal{D}}$
-modules. In this paper, we use the notion of crystalline
${\mathcal{D}}$
-modules. In this paper, we use the notion of crystalline
![]() ${\mathcal{D}}$
-modules, i.e.,
${\mathcal{D}}$
-modules, i.e.,
![]() ${\mathcal{D}}$
-modules are quasi-coherent sheaves with a flat connection. Likewise, the stack
${\mathcal{D}}$
-modules are quasi-coherent sheaves with a flat connection. Likewise, the stack
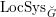 $\operatorname{LocSys}_{\breve{G}}$
is the stack of
$\operatorname{LocSys}_{\breve{G}}$
is the stack of
![]() $\breve{G}$
-bundles on
$\breve{G}$
-bundles on
![]() $C$
with a flat connection.
$C$
with a flat connection.
1.2 Summary of the construction
The case
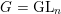 $G=\operatorname{GL}_{n}$
has been considered by Bezrukavnikov and Braverman in [Reference Bezrukavnikov and BravermanBB07] (see [Reference GroechenigGro12, Reference TravkinTra11] for various extensions). The main observation is that the geometric Langlands duality in characteristic
$G=\operatorname{GL}_{n}$
has been considered by Bezrukavnikov and Braverman in [Reference Bezrukavnikov and BravermanBB07] (see [Reference GroechenigGro12, Reference TravkinTra11] for various extensions). The main observation is that the geometric Langlands duality in characteristic
![]() $p$
formulated in the above form can be thought as a twisted version of its classical limit. Since the classical duality holds ‘generically’, they proved a ‘generic’ version of the GLC in the case when
$p$
formulated in the above form can be thought as a twisted version of its classical limit. Since the classical duality holds ‘generically’, they proved a ‘generic’ version of the GLC in the case when
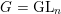 $G=\operatorname{GL}_{n}$
.
$G=\operatorname{GL}_{n}$
.
Our generalization to any semi-simple group
![]() $G$
is based on the same observation, but some new ingredients are needed in this general situation.
$G$
is based on the same observation, but some new ingredients are needed in this general situation.
One of the main difficulties for general
![]() $G$
is that the classical duality is more complicated. For
$G$
is that the classical duality is more complicated. For
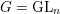 $G=\operatorname{GL}_{n}$
, the generic fibers of the Hitchin fibration are the Picard stacks of line bundles on the corresponding spectral curves and the duality of Hitchin fibrations in this case essentially amounts to the self-duality of the Jacobian of an algebraic curve. However, for general
$G=\operatorname{GL}_{n}$
, the generic fibers of the Hitchin fibration are the Picard stacks of line bundles on the corresponding spectral curves and the duality of Hitchin fibrations in this case essentially amounts to the self-duality of the Jacobian of an algebraic curve. However, for general
![]() $G$
, the fibers of the Hitchin fibration involve more general Picard stacks, such as the Prym varieties etc., and the duality of the Hitchin fibrations for
$G$
, the fibers of the Hitchin fibration involve more general Picard stacks, such as the Prym varieties etc., and the duality of the Hitchin fibrations for
![]() $G$
and
$G$
and
![]() $\breve{G}$
over
$\breve{G}$
over
![]() $\mathbb{C}$
are the main theme of [Reference Donagi and PantevDP12] (see [Reference Hausel and ThaddeusHT03] for the case
$\mathbb{C}$
are the main theme of [Reference Donagi and PantevDP12] (see [Reference Hausel and ThaddeusHT03] for the case
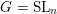 $G=\operatorname{SL}_{n}$
). As commented on by the authors, the arguments in [Reference Donagi and PantevDP12] use transcendental methods in an essential way and therefore cannot be applied to our situation directly.
$G=\operatorname{SL}_{n}$
). As commented on by the authors, the arguments in [Reference Donagi and PantevDP12] use transcendental methods in an essential way and therefore cannot be applied to our situation directly.
Our first step is to extend the classical duality to any reductive group
![]() $G$
over any algebraically closed field
$G$
over any algebraically closed field
![]() $k$
whose characteristic does not divide the order of the Weyl group of
$k$
whose characteristic does not divide the order of the Weyl group of
![]() $G$
. Let us first give its statement, and leave the details to §3. For a reductive group
$G$
. Let us first give its statement, and leave the details to §3. For a reductive group
![]() $G$
and a smooth projective curve
$G$
and a smooth projective curve
![]() $C$
over
$C$
over
![]() $k$
, and a positive line bundle
$k$
, and a positive line bundle
![]() ${\mathcal{L}}$
on
${\mathcal{L}}$
on
![]() $C$
, let
$C$
, let
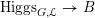 $\operatorname{Higgs}_{G,{\mathcal{L}}}\rightarrow B$
denote the corresponding Hitchin fibration, on which the Picard stack
$\operatorname{Higgs}_{G,{\mathcal{L}}}\rightarrow B$
denote the corresponding Hitchin fibration, on which the Picard stack
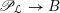 $\mathscr{P}_{{\mathcal{L}}}\rightarrow B$
acts (see §2 for a review). There is an open subset
$\mathscr{P}_{{\mathcal{L}}}\rightarrow B$
acts (see §2 for a review). There is an open subset
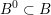 $B^{0}\subset B$
such that
$B^{0}\subset B$
such that
![]() $\mathscr{P}_{{\mathcal{L}}}|_{B^{0}}$
is a Beilinson
$\mathscr{P}_{{\mathcal{L}}}|_{B^{0}}$
is a Beilinson
![]() $1$
-motive (a Picard stack that is essentially an abelian variety, see Appendix A). Fixing a non-degenerate bilinear form on the Lie algebra
$1$
-motive (a Picard stack that is essentially an abelian variety, see Appendix A). Fixing a non-degenerate bilinear form on the Lie algebra
![]() $\mathfrak{g}$
of
$\mathfrak{g}$
of
![]() $G$
, one can identify the Hitchin base
$G$
, one can identify the Hitchin base
![]() $B$
and the corresponding open subset
$B$
and the corresponding open subset
![]() $B^{0}$
for
$B^{0}$
for
![]() $G$
and
$G$
and
![]() $\breve{G}$
. The classical duality is the following assertion.
$\breve{G}$
. The classical duality is the following assertion.
Theorem 1.2.1. For a positive line bundle
![]() ${\mathcal{L}}$
on
${\mathcal{L}}$
on
![]() $C$
, there is a canonical isomorphism of Picard stacks
$C$
, there is a canonical isomorphism of Picard stacks
 $$\begin{eqnarray}\mathfrak{D}_{\text{cl}}:(\mathscr{P}_{{\mathcal{L}}}|_{B^{0}})^{\vee }\simeq \breve{\mathscr{P}}_{{\mathcal{L}}}|_{B^{0}},\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{D}_{\text{cl}}:(\mathscr{P}_{{\mathcal{L}}}|_{B^{0}})^{\vee }\simeq \breve{\mathscr{P}}_{{\mathcal{L}}}|_{B^{0}},\end{eqnarray}$$
where
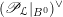 $(\mathscr{P}_{{\mathcal{L}}}|_{B^{0}})^{\vee }$
is the dual Picard stack of
$(\mathscr{P}_{{\mathcal{L}}}|_{B^{0}})^{\vee }$
is the dual Picard stack of
![]() $\mathscr{P}_{{\mathcal{L}}}|_{B^{0}}$
(as defined in Appendix A).
$\mathscr{P}_{{\mathcal{L}}}|_{B^{0}}$
(as defined in Appendix A).
Now assume that the characteristic of
![]() $k$
is positive. In addition, assume that the genus of
$k$
is positive. In addition, assume that the genus of
![]() $C$
is at least two and that
$C$
is at least two and that
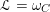 ${\mathcal{L}}=\unicode[STIX]{x1D714}_{C}$
is the canonical bundle. We will omit the subscript
${\mathcal{L}}=\unicode[STIX]{x1D714}_{C}$
is the canonical bundle. We will omit the subscript
![]() $\unicode[STIX]{x1D714}_{C}$
and write
$\unicode[STIX]{x1D714}_{C}$
and write
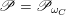 $\mathscr{P}=\mathscr{P}_{\unicode[STIX]{x1D714}_{C}}$
etc. The second step then is to construct a twisted version of the above classical duality in this situation. To explain its meaning, let us first introduce a notation: if
$\mathscr{P}=\mathscr{P}_{\unicode[STIX]{x1D714}_{C}}$
etc. The second step then is to construct a twisted version of the above classical duality in this situation. To explain its meaning, let us first introduce a notation: if
![]() $X$
is a stack over
$X$
is a stack over
![]() $k$
, we denote by
$k$
, we denote by
![]() $X^{\prime }$
its Frobenius twist, i.e., the pullback of
$X^{\prime }$
its Frobenius twist, i.e., the pullback of
![]() $X$
along the absolute Frobenius endomorphism of
$X$
along the absolute Frobenius endomorphism of
![]() $k$
. Let
$k$
. Let
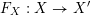 $F_{X}:X\rightarrow X^{\prime }$
denote the relative Frobenius morphism. We will replace both sides of (1.2.1) by certain torsors under
$F_{X}:X\rightarrow X^{\prime }$
denote the relative Frobenius morphism. We will replace both sides of (1.2.1) by certain torsors under
![]() ${\mathscr{P}^{\prime }}^{\vee }$
and
${\mathscr{P}^{\prime }}^{\vee }$
and
![]() $\breve{\mathscr{P}}^{\prime }$
.
$\breve{\mathscr{P}}^{\prime }$
.
We begin to explain the
![]() $\breve{\mathscr{P}}^{\prime }$
-torsor
$\breve{\mathscr{P}}^{\prime }$
-torsor
![]() $\breve{\mathscr{H}}$
, which was introduced in [Reference Chen and ZhuCZ15]. There is a smooth commutative group scheme
$\breve{\mathscr{H}}$
, which was introduced in [Reference Chen and ZhuCZ15]. There is a smooth commutative group scheme
![]() $\breve{J}^{\prime }$
on
$\breve{J}^{\prime }$
on
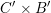 $C^{\prime }\times B^{\prime }$
and
$C^{\prime }\times B^{\prime }$
and
![]() $\breve{\mathscr{P}}^{\prime }$
in fact classifies
$\breve{\mathscr{P}}^{\prime }$
in fact classifies
![]() $\breve{J}^{\prime }$
-torsors. Let us denote by
$\breve{J}^{\prime }$
-torsors. Let us denote by
![]() $\breve{J}^{p}$
the pullback of
$\breve{J}^{p}$
the pullback of
![]() $\breve{J}^{\prime }$
along the relative Frobenius
$\breve{J}^{\prime }$
along the relative Frobenius
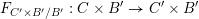 $F_{C^{\prime }\times B^{\prime }/B^{\prime }}:C\times B^{\prime }\rightarrow C^{\prime }\times B^{\prime }$
. This is a group scheme with a canonical connection along
$F_{C^{\prime }\times B^{\prime }/B^{\prime }}:C\times B^{\prime }\rightarrow C^{\prime }\times B^{\prime }$
. This is a group scheme with a canonical connection along
![]() $C$
, and therefore it makes sense to talk about
$C$
, and therefore it makes sense to talk about
![]() $\breve{J}^{p}$
-local systems on
$\breve{J}^{p}$
-local systems on
![]() $C\times B^{\prime }$
and their
$C\times B^{\prime }$
and their
![]() $p$
-curvatures (see [Reference Chen and ZhuCZ15, Appendix] for generalities). Let
$p$
-curvatures (see [Reference Chen and ZhuCZ15, Appendix] for generalities). Let
![]() $\breve{\mathscr{H}}$
be the stack of
$\breve{\mathscr{H}}$
be the stack of
![]() $\breve{J}^{p}$
-local systems with some specific
$\breve{J}^{p}$
-local systems with some specific
![]() $p$
-curvature
$p$
-curvature
![]() $\breve{\unicode[STIX]{x1D70F}}^{\prime }$
. This is a
$\breve{\unicode[STIX]{x1D70F}}^{\prime }$
. This is a
![]() $\breve{\mathscr{P}}^{\prime }$
-torsor.
$\breve{\mathscr{P}}^{\prime }$
-torsor.
Next we explain the
![]() ${\mathscr{P}^{\prime }}^{\vee }$
-torsor
${\mathscr{P}^{\prime }}^{\vee }$
-torsor
![]() $\mathscr{T}_{\mathscr{D}(\unicode[STIX]{x1D703}_{m})}$
. According to general nonsense (Appendix A), such a torsor gives a multiplicative
$\mathscr{T}_{\mathscr{D}(\unicode[STIX]{x1D703}_{m})}$
. According to general nonsense (Appendix A), such a torsor gives a multiplicative
![]() $\mathbb{G}_{m}$
-gerbe
$\mathbb{G}_{m}$
-gerbe
![]() $\mathscr{D}$
on
$\mathscr{D}$
on
![]() $\mathscr{P}^{\prime }$
and vice versa. So it is enough to explain this multiplicative
$\mathscr{P}^{\prime }$
and vice versa. So it is enough to explain this multiplicative
![]() $\mathbb{G}_{m}$
-gerbe
$\mathbb{G}_{m}$
-gerbe
![]() $\mathscr{D}(\unicode[STIX]{x1D703}_{m})$
on
$\mathscr{D}(\unicode[STIX]{x1D703}_{m})$
on
![]() $\mathscr{P}^{\prime }$
. First recall that the sheaf of crystalline differential operators on
$\mathscr{P}^{\prime }$
. First recall that the sheaf of crystalline differential operators on
![]() $\mathscr{P}$
can be regarded as a
$\mathscr{P}$
can be regarded as a
![]() $\mathbb{G}_{m}$
-gerbe
$\mathbb{G}_{m}$
-gerbe
![]() $\mathscr{D}_{\mathscr{P}}$
on the cotangent bundle
$\mathscr{D}_{\mathscr{P}}$
on the cotangent bundle
![]() $T^{\ast }\mathscr{P}^{\prime }$
. We will construct a 1-form
$T^{\ast }\mathscr{P}^{\prime }$
. We will construct a 1-form
![]() $\unicode[STIX]{x1D703}_{m}$
on
$\unicode[STIX]{x1D703}_{m}$
on
![]() $\mathscr{P}^{\prime }$
, which is multiplicative (in the sense of §C.2). Now,
$\mathscr{P}^{\prime }$
, which is multiplicative (in the sense of §C.2). Now,
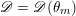 $\mathscr{D}=\mathscr{D}(\unicode[STIX]{x1D703}_{m})$
is the gerbe on
$\mathscr{D}=\mathscr{D}(\unicode[STIX]{x1D703}_{m})$
is the gerbe on
![]() $\mathscr{P}^{\prime }$
obtained via pullback of
$\mathscr{P}^{\prime }$
obtained via pullback of
![]() $\mathscr{D}_{\mathscr{P}}$
along the map
$\mathscr{D}_{\mathscr{P}}$
along the map
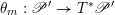 $\unicode[STIX]{x1D703}_{m}:\mathscr{P}^{\prime }\rightarrow T^{\ast }\mathscr{P}^{\prime }$
.
$\unicode[STIX]{x1D703}_{m}:\mathscr{P}^{\prime }\rightarrow T^{\ast }\mathscr{P}^{\prime }$
.
The twisted version of the classical duality is the following assertion.
Theorem 1.2.2. Over
![]() $B^{^{\prime }0}$
, there is a canonical isomorphism of
$B^{^{\prime }0}$
, there is a canonical isomorphism of
 ${\mathscr{P}^{\prime }}^{\vee }\simeq \breve{\mathscr{P}}^{\prime }$
-torsors
${\mathscr{P}^{\prime }}^{\vee }\simeq \breve{\mathscr{P}}^{\prime }$
-torsors
 $$\begin{eqnarray}\mathfrak{D}:\mathscr{T}_{\mathscr{D}(\unicode[STIX]{x1D703}_{m})}|_{B^{^{\prime }0}}\simeq \breve{\mathscr{H}}|_{B^{^{\prime }0}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{D}:\mathscr{T}_{\mathscr{D}(\unicode[STIX]{x1D703}_{m})}|_{B^{^{\prime }0}}\simeq \breve{\mathscr{H}}|_{B^{^{\prime }0}}.\end{eqnarray}$$
The final step towards (1.1.1) is to establish two abelianization theorems. Another difference between the geometric Langlands correspondence for
![]() $\operatorname{GL}_{n}$
and for a general group
$\operatorname{GL}_{n}$
and for a general group
![]() $G$
is that in the latter case, there is no canonical equivalence in general. As is widely known to experts (e.g. see [Reference Frenkel and WittenFW08]), the geometric Langlands correspondence for general
$G$
is that in the latter case, there is no canonical equivalence in general. As is widely known to experts (e.g. see [Reference Frenkel and WittenFW08]), the geometric Langlands correspondence for general
![]() $G$
should depend on a choice of theta characteristic of the curve
$G$
should depend on a choice of theta characteristic of the curve
![]() $C$
.
$C$
.
Let us fix a square root
![]() $\unicode[STIX]{x1D705}$
of
$\unicode[STIX]{x1D705}$
of
![]() $\unicode[STIX]{x1D714}_{C}$
. Then the Kostant section of
$\unicode[STIX]{x1D714}_{C}$
. Then the Kostant section of
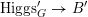 $\operatorname{Higgs}_{G}^{\prime }\rightarrow B^{\prime }$
induces a map
$\operatorname{Higgs}_{G}^{\prime }\rightarrow B^{\prime }$
induces a map
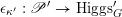 $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}^{\prime }}:\mathscr{P}^{\prime }\rightarrow \operatorname{Higgs}_{G}^{\prime }$
. The first abelianization theorem asserts a canonical isomorphism
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}^{\prime }}:\mathscr{P}^{\prime }\rightarrow \operatorname{Higgs}_{G}^{\prime }$
. The first abelianization theorem asserts a canonical isomorphism
 $$\begin{eqnarray}\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}^{\prime }}^{\ast }\mathscr{D}_{\operatorname{ Bun}_{G}}\simeq \mathscr{D}(\unicode[STIX]{x1D703}_{m}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}^{\prime }}^{\ast }\mathscr{D}_{\operatorname{ Bun}_{G}}\simeq \mathscr{D}(\unicode[STIX]{x1D703}_{m}),\end{eqnarray}$$
where
![]() $\mathscr{D}_{\operatorname{Bun}_{G}}$
is the
$\mathscr{D}_{\operatorname{Bun}_{G}}$
is the
![]() $\mathbb{G}_{m}$
-gerbe (on
$\mathbb{G}_{m}$
-gerbe (on
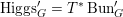 $\operatorname{Higgs}_{G}^{\prime }=T^{\ast }\operatorname{Bun}_{G}^{\prime }$
) of crystalline differential operators on
$\operatorname{Higgs}_{G}^{\prime }=T^{\ast }\operatorname{Bun}_{G}^{\prime }$
) of crystalline differential operators on
![]() $\operatorname{Bun}_{G}$
and
$\operatorname{Bun}_{G}$
and
![]() $\mathscr{D}(\unicode[STIX]{x1D703}_{m})$
is the
$\mathscr{D}(\unicode[STIX]{x1D703}_{m})$
is the
![]() $\mathbb{G}_{m}$
-gerbe on
$\mathbb{G}_{m}$
-gerbe on
![]() $\mathscr{P}^{\prime }$
mentioned above.
$\mathscr{P}^{\prime }$
mentioned above.
On the dual side, we constructed a canonical morphism in [Reference Chen and ZhuCZ15]
 $$\begin{eqnarray}\mathfrak{C}:\breve{\mathscr{H}}\times ^{\breve{\mathscr{P}}^{\prime }}\operatorname{Higgs}_{\breve{G}}^{\prime }\rightarrow \operatorname{LocSys}_{\breve{G}},\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{C}:\breve{\mathscr{H}}\times ^{\breve{\mathscr{P}}^{\prime }}\operatorname{Higgs}_{\breve{G}}^{\prime }\rightarrow \operatorname{LocSys}_{\breve{G}},\end{eqnarray}$$
and the Kostant section of
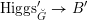 $\operatorname{Higgs}_{\breve{G}}^{\prime }\rightarrow B^{\prime }$
induces an isomorphism
$\operatorname{Higgs}_{\breve{G}}^{\prime }\rightarrow B^{\prime }$
induces an isomorphism
 $$\begin{eqnarray}\mathfrak{C}_{\unicode[STIX]{x1D705}}^{}:\breve{\mathscr{H}}\simeq \operatorname{LocSys}_{\breve{G}}^{\text{reg}},\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{C}_{\unicode[STIX]{x1D705}}^{}:\breve{\mathscr{H}}\simeq \operatorname{LocSys}_{\breve{G}}^{\text{reg}},\end{eqnarray}$$
where
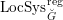 $\operatorname{LocSys}_{\breve{G}}^{\text{reg}}$
is a certain open substack of
$\operatorname{LocSys}_{\breve{G}}^{\text{reg}}$
is a certain open substack of
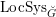 $\operatorname{LocSys}_{\breve{G}}$
(see [Reference Chen and ZhuCZ15, Remark 3.14]).
$\operatorname{LocSys}_{\breve{G}}$
(see [Reference Chen and ZhuCZ15, Remark 3.14]).
Combining the above three steps and a general version of the Fourier–Mukai transform (Appendix A) will give the desired equivalence (1.1.1).
Let us mention that the morphism
![]() $\mathfrak{C}$
was obtained in [Reference Chen and ZhuCZ15] as a version of Simpson correspondence for smooth projective curves in positive characteristic.
$\mathfrak{C}$
was obtained in [Reference Chen and ZhuCZ15] as a version of Simpson correspondence for smooth projective curves in positive characteristic.
Finally in §§5.5 and 5.6, we discuss how the equivalence constructed above depends on the choice of the theta characteristic. This can be regarded as a verification of the predictions of [Reference Frenkel and WittenFW08, §10] in our settings.
1.3 The Langlands transform
To claim that the above equivalence is the conjectural geometric Langlands transform, one needs to verify several properties that it is supposed to satisfy. We will only briefly discuss these properties (see [Reference GaitsgoryGai13] for more details), and leave the verifications to our next work.
The first property is that the equivalence should intertwine the action of the Hecke operators on the automorphic side and the action of the Wilson operators on the spectral side. Recall that in the case
![]() $k=\mathbb{C}$
, both categories
$k=\mathbb{C}$
, both categories
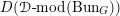 $D({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G}))$
and
$D({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G}))$
and
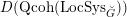 $D(\operatorname{Qcoh}(\operatorname{LocSys}_{\breve{G}}))$
admit actions of a family of commuting operators, labeled by points
$D(\operatorname{Qcoh}(\operatorname{LocSys}_{\breve{G}}))$
admit actions of a family of commuting operators, labeled by points
![]() $x$
on the curve and representations
$x$
on the curve and representations
![]() $V$
of the group
$V$
of the group
![]() $\breve{G}$
. Namely, for
$\breve{G}$
. Namely, for
![]() $x\in C$
and
$x\in C$
and
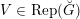 $V\in \operatorname{Rep}(\breve{G})$
, there is the so-called Wilson operator
$V\in \operatorname{Rep}(\breve{G})$
, there is the so-called Wilson operator
![]() $W_{V,x}$
acting on
$W_{V,x}$
acting on
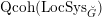 $\operatorname{Qcoh}(\operatorname{LocSys}_{\breve{G}})$
by tensoring with the locally free sheaf
$\operatorname{Qcoh}(\operatorname{LocSys}_{\breve{G}})$
by tensoring with the locally free sheaf
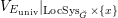 $V_{E_{\text{univ}}}|_{\operatorname{LocSys}_{\breve{G}}\times \{x\}}$
. On the other side, there is the Hecke operator
$V_{E_{\text{univ}}}|_{\operatorname{LocSys}_{\breve{G}}\times \{x\}}$
. On the other side, there is the Hecke operator
![]() $H_{V,x}$
acting on
$H_{V,x}$
acting on
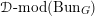 ${\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})$
via certain integral transform (e.g. see [Reference Beilinson and DrinfeldBD91, §5]). The second property is that the equivalence should satisfy the Whittaker normalization. Namely, the Whittaker
${\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})$
via certain integral transform (e.g. see [Reference Beilinson and DrinfeldBD91, §5]). The second property is that the equivalence should satisfy the Whittaker normalization. Namely, the Whittaker
![]() ${\mathcal{D}}$
-module
${\mathcal{D}}$
-module
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D6F9}}$
on
${\mathcal{F}}_{\unicode[STIX]{x1D6F9}}$
on
![]() $\operatorname{Bun}_{G}$
is supposed to transformed to the structure sheaf
$\operatorname{Bun}_{G}$
is supposed to transformed to the structure sheaf
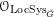 ${\mathcal{O}}_{\operatorname{LocSys}_{\breve{G}}}$
.
${\mathcal{O}}_{\operatorname{LocSys}_{\breve{G}}}$
.
In the positive characteristic, it is yet not clear how to define Hecke operators (except those corresponding to minuscule coweights) due to lack of the notion of intersection cohomology
![]() ${\mathcal{D}}$
-modules. Our observation is that by the geometric Casselman–Shalika formula [Reference Frenkel, Gaitsgory and VilonenFGV01], the two properties together will imply that the Whittaker coefficients of
${\mathcal{D}}$
-modules. Our observation is that by the geometric Casselman–Shalika formula [Reference Frenkel, Gaitsgory and VilonenFGV01], the two properties together will imply that the Whittaker coefficients of
![]() ${\mathcal{D}}$
-modules on
${\mathcal{D}}$
-modules on
![]() $\operatorname{Bun}_{G}$
can be calculated by applying the Wilson operators on their Langlands transforms and then taking the global sections. This is a well formulated statement in characteristic
$\operatorname{Bun}_{G}$
can be calculated by applying the Wilson operators on their Langlands transforms and then taking the global sections. This is a well formulated statement in characteristic
![]() $p$
and we will verify in the future work that this is satisfied by the equivalence constructed here.
$p$
and we will verify in the future work that this is satisfied by the equivalence constructed here.
The third property is that the equivalence should be compatible with Beilinson and Drinfeld’s construction of automorphic
![]() ${\mathcal{D}}$
-modules via opers [Reference Beilinson and DrinfeldBD91]. In the case
${\mathcal{D}}$
-modules via opers [Reference Beilinson and DrinfeldBD91]. In the case
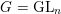 $G=\operatorname{GL}_{n}$
this property has been verified in [Reference Bezrukavnikov and TravkinBT16]. We plan to return to this in the future work.
$G=\operatorname{GL}_{n}$
this property has been verified in [Reference Bezrukavnikov and TravkinBT16]. We plan to return to this in the future work.
1.4 Structure of the article
Let us now describe the contents of this paper in more detail.
In §2 we collect some facts about Hitchin fibrations that are used in this paper. Main references are [Reference NgôNgô06, Reference NgôNgô10].
In §3 we prove the classical duality, i.e., the duality of Hitchin fibrations. This extends the work of [Reference Donagi and PantevDP12] (over
![]() $\mathbb{C}$
) to any algebraically closed field whose characteristic does not divide the order of the Weyl group of
$\mathbb{C}$
) to any algebraically closed field whose characteristic does not divide the order of the Weyl group of
![]() $G$
. In §3.7, we discuss the compatibility of the classical duality with twisting by
$G$
. In §3.7, we discuss the compatibility of the classical duality with twisting by
![]() $Z(\breve{G})$
-torsors. This is used to study the dependence of the equivalence (1.1.1) on the choice of the theta characteristic in §§5.5 and 5.6.
$Z(\breve{G})$
-torsors. This is used to study the dependence of the equivalence (1.1.1) on the choice of the theta characteristic in §§5.5 and 5.6.
In §4 we construct a canonical multiplicative 1-form
![]() $\unicode[STIX]{x1D703}_{m}$
on
$\unicode[STIX]{x1D703}_{m}$
on
![]() $\mathscr{P}^{\prime }$
.
$\mathscr{P}^{\prime }$
.
In §5 we deduce our main Theorem 5.0.1 from the twisted duality (see §5.2) and the two abelianization theorems (see §5.3).
There are three appendices at the end of the paper.
In Appendix A we collect some basic facts about Beilinson
![]() $1$
-motives and duality on Beilinson
$1$
-motives and duality on Beilinson
![]() $1$
-motives. In particular, we state a general version of Fourier–Mukai transforms for Beilinson
$1$
-motives. In particular, we state a general version of Fourier–Mukai transforms for Beilinson
![]() $1$
-motives.
$1$
-motives.
In Appendix B we recall the basic theory of
![]() ${\mathcal{D}}$
-modules over varieties and stacks in positive characteristic, following [Reference Bezrukavnikov, Mirković and RumyninBMR08, Reference Bezrukavnikov and BravermanBB07, Reference Ogus and VologodskyOV07, Reference TravkinTra11].
${\mathcal{D}}$
-modules over varieties and stacks in positive characteristic, following [Reference Bezrukavnikov, Mirković and RumyninBMR08, Reference Bezrukavnikov and BravermanBB07, Reference Ogus and VologodskyOV07, Reference TravkinTra11].
In Appendix C we prove the abelian duality for good Beilinson
![]() $1$
-motives. It asserts that the derived category of
$1$
-motives. It asserts that the derived category of
![]() ${\mathcal{D}}$
-modules on a ‘good’ Beilinson
${\mathcal{D}}$
-modules on a ‘good’ Beilinson
![]() $1$
-motive
$1$
-motive
![]() $\mathscr{A}$
is equivalent to the derived category of quasi-coherent sheaves on the universal extension
$\mathscr{A}$
is equivalent to the derived category of quasi-coherent sheaves on the universal extension
![]() $\mathscr{A}^{\natural }$
by vector groups of its dual
$\mathscr{A}^{\natural }$
by vector groups of its dual
![]() $\mathscr{A}^{\vee }$
.
$\mathscr{A}^{\vee }$
.
1.5 Notations
1.5.1 Notations related to algebraic stacks
Our terminology of algebraic stacks follows the book [Reference Laumon and Moret-BaillyLB00]. Let
![]() $k$
be an algebraically closed field and let
$k$
be an algebraically closed field and let
![]() $p$
be the characteristic component of
$p$
be the characteristic component of
![]() $k$
. Let
$k$
. Let
![]() $S$
be a Noetherian scheme over
$S$
be a Noetherian scheme over
![]() $k$
. In this paper, an algebraic stack
$k$
. In this paper, an algebraic stack
![]() $\mathscr{X}$
over
$\mathscr{X}$
over
![]() $S$
is a stack such that the diagonal morphism
$S$
is a stack such that the diagonal morphism
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{S}:\mathscr{X}\rightarrow \mathscr{X}\times _{S}\mathscr{X}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{S}:\mathscr{X}\rightarrow \mathscr{X}\times _{S}\mathscr{X}\end{eqnarray}$$
is representable and quasi-compact and such that there exists a smooth presentation, i.e., a smooth, surjective morphism
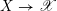 $X\rightarrow \mathscr{X}$
from a scheme
$X\rightarrow \mathscr{X}$
from a scheme
![]() $X$
.
$X$
.
An algebraic stack
![]() $\mathscr{X}$
is called smooth over
$\mathscr{X}$
is called smooth over
![]() $S$
if for every
$S$
if for every
![]() $S$
-scheme
$S$
-scheme
![]() $U$
mapping smoothly to
$U$
mapping smoothly to
![]() $\mathscr{X}$
, the structure morphism
$\mathscr{X}$
, the structure morphism
![]() $U\rightarrow S$
is smooth.
$U\rightarrow S$
is smooth.
For any algebraic stack
![]() $\mathscr{X}$
, we denote by
$\mathscr{X}$
, we denote by
![]() $\mathscr{X}_{\acute{\text{E}}\text{t}}$
the big étale site of
$\mathscr{X}_{\acute{\text{E}}\text{t}}$
the big étale site of
![]() $\mathscr{X}$
. We denote by
$\mathscr{X}$
. We denote by
![]() $\mathscr{X}_{\text{sm}}$
the smooth site on
$\mathscr{X}_{\text{sm}}$
the smooth site on
![]() $\mathscr{X}$
, i.e., the site for which the underling category has objects consisting of
$\mathscr{X}$
, i.e., the site for which the underling category has objects consisting of
![]() $S$
-schemes
$S$
-schemes
![]() $U$
together with a smooth morphism
$U$
together with a smooth morphism
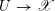 $U\rightarrow \mathscr{X}$
and has morphisms
$U\rightarrow \mathscr{X}$
and has morphisms
![]() $V\rightarrow U$
smooth 2-morphisms over
$V\rightarrow U$
smooth 2-morphisms over
![]() $\mathscr{X}$
and for which covering maps are smooth surjective maps of schemes. If
$\mathscr{X}$
and for which covering maps are smooth surjective maps of schemes. If
![]() $\mathscr{X}$
is a Deligne–Mumford stack, we denote by
$\mathscr{X}$
is a Deligne–Mumford stack, we denote by
![]() $\mathscr{X}_{\acute{\text{e}}\text{t}}$
the small étale site of
$\mathscr{X}_{\acute{\text{e}}\text{t}}$
the small étale site of
![]() $\mathscr{X}$
.
$\mathscr{X}$
.
Let
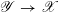 $\mathscr{Y}\rightarrow \mathscr{X}$
be a quasi-projective morphism of algebraic stacks, with
$\mathscr{Y}\rightarrow \mathscr{X}$
be a quasi-projective morphism of algebraic stacks, with
![]() $\mathscr{X}$
smooth and proper over
$\mathscr{X}$
smooth and proper over
![]() $S$
. We denote by
$S$
. We denote by
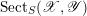 $\operatorname{Sect}_{S}(\mathscr{X},\mathscr{Y})$
the stack of ‘sections’ of
$\operatorname{Sect}_{S}(\mathscr{X},\mathscr{Y})$
the stack of ‘sections’ of
![]() $\mathscr{Y}$
over
$\mathscr{Y}$
over
![]() $\mathscr{X}$
, i.e., for any
$\mathscr{X}$
, i.e., for any
 $u:U\rightarrow S$
we have
$u:U\rightarrow S$
we have
 $$\begin{eqnarray}\operatorname{Sect}_{S}(\mathscr{X},\mathscr{Y})(U)=\operatorname{Hom}_{\mathscr{X}}(\mathscr{X}\times _{S}U,\mathscr{Y}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Sect}_{S}(\mathscr{X},\mathscr{Y})(U)=\operatorname{Hom}_{\mathscr{X}}(\mathscr{X}\times _{S}U,\mathscr{Y}).\end{eqnarray}$$
If the base scheme
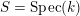 $S=\operatorname{Spec}(k)$
, we write
$S=\operatorname{Spec}(k)$
, we write
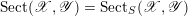 $\operatorname{Sect}(\mathscr{X},\mathscr{Y})=\operatorname{Sect}_{S}(\mathscr{X},\mathscr{Y})$
.
$\operatorname{Sect}(\mathscr{X},\mathscr{Y})=\operatorname{Sect}_{S}(\mathscr{X},\mathscr{Y})$
.
If
![]() $\mathscr{X}$
is a smooth algebraic stack over
$\mathscr{X}$
is a smooth algebraic stack over
![]() $S$
, we define the relative tangent stack
$S$
, we define the relative tangent stack
 $T(\mathscr{X}/S)$
as the stack that assigns every
$T(\mathscr{X}/S)$
as the stack that assigns every
 $\operatorname{Spec}R\rightarrow S$
, the groupoid
$\operatorname{Spec}R\rightarrow S$
, the groupoid
 $$\begin{eqnarray}T(\mathscr{X}/S)(R):=\mathscr{X}(R[\unicode[STIX]{x1D716}]/\unicode[STIX]{x1D716}^{2}).\end{eqnarray}$$
$$\begin{eqnarray}T(\mathscr{X}/S)(R):=\mathscr{X}(R[\unicode[STIX]{x1D716}]/\unicode[STIX]{x1D716}^{2}).\end{eqnarray}$$
It is algebraic and the natural inclusion
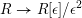 $R\rightarrow R[\unicode[STIX]{x1D716}]/\unicode[STIX]{x1D716}^{2}$
induces a morphism
$R\rightarrow R[\unicode[STIX]{x1D716}]/\unicode[STIX]{x1D716}^{2}$
induces a morphism
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}_{\mathscr{X}}:T(\mathscr{X}/S)\rightarrow \mathscr{X}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{\mathscr{X}}:T(\mathscr{X}/S)\rightarrow \mathscr{X}.\end{eqnarray}$$
It is known that
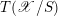 $T(\mathscr{X}/S)$
is a relative Picard stack over
$T(\mathscr{X}/S)$
is a relative Picard stack over
![]() $\mathscr{X}$
. Therefore, one can associate to it a complex in
$\mathscr{X}$
. Therefore, one can associate to it a complex in
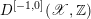 $D^{[-1,0]}(\mathscr{X},\mathbb{Z})$
, called the relative tangent complex:
$D^{[-1,0]}(\mathscr{X},\mathbb{Z})$
, called the relative tangent complex:
 $$\begin{eqnarray}T_{\mathscr{X}/S}^{\bullet }=\{T_{\mathscr{ X}/S}\rightarrow T_{\mathscr{X}}\}.\end{eqnarray}$$
$$\begin{eqnarray}T_{\mathscr{X}/S}^{\bullet }=\{T_{\mathscr{ X}/S}\rightarrow T_{\mathscr{X}}\}.\end{eqnarray}$$
The relative cotangent stack is then defined as
 $$\begin{eqnarray}T^{\ast }(\mathscr{X}/S):=\operatorname{Spec}_{\mathscr{ X}}(\operatorname{Sym}_{{\mathcal{O}}_{\mathscr{X}}}H^{0}(T_{\mathscr{ X}/S}^{\bullet })).\end{eqnarray}$$
$$\begin{eqnarray}T^{\ast }(\mathscr{X}/S):=\operatorname{Spec}_{\mathscr{ X}}(\operatorname{Sym}_{{\mathcal{O}}_{\mathscr{X}}}H^{0}(T_{\mathscr{ X}/S}^{\bullet })).\end{eqnarray}$$
Let
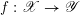 $f:\mathscr{X}\rightarrow \mathscr{Y}$
be a (representable) morphism between two algebraic stacks over
$f:\mathscr{X}\rightarrow \mathscr{Y}$
be a (representable) morphism between two algebraic stacks over
![]() $S$
. We denote the cotangent morphism as the following diagram of maps.
$S$
. We denote the cotangent morphism as the following diagram of maps.

1.5.2 Notations related to Frobenius morphism
Let
![]() $S$
be a Noetherian
$S$
be a Noetherian
![]() $k$
-scheme and
$k$
-scheme and
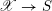 $\mathscr{X}\rightarrow S$
be an algebraic stack over
$\mathscr{X}\rightarrow S$
be an algebraic stack over
![]() $S$
. If
$S$
. If
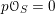 $p{\mathcal{O}}_{S}=0$
, we denote by
$p{\mathcal{O}}_{S}=0$
, we denote by
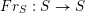 $Fr_{S}:S\rightarrow S$
the absolute Frobenius map of
$Fr_{S}:S\rightarrow S$
the absolute Frobenius map of
![]() $S$
. We have the following commutative diagram
$S$
. We have the following commutative diagram

where the square is Cartesian. We call
![]() $\mathscr{X}^{(S)}$
the Frobenius twist of
$\mathscr{X}^{(S)}$
the Frobenius twist of
![]() $\mathscr{X}$
along
$\mathscr{X}$
along
![]() $S$
, and
$S$
, and
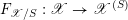 $F_{\mathscr{X}/S}:\mathscr{X}\rightarrow \mathscr{X}^{(S)}$
the relative Frobenius morphism. If the base scheme
$F_{\mathscr{X}/S}:\mathscr{X}\rightarrow \mathscr{X}^{(S)}$
the relative Frobenius morphism. If the base scheme
![]() $S$
is clear,
$S$
is clear,
![]() $\mathscr{X}^{(S)}$
is also denoted by
$\mathscr{X}^{(S)}$
is also denoted by
![]() $\mathscr{X}^{\prime }$
for simplicity.
$\mathscr{X}^{\prime }$
for simplicity.
1.5.3 Notation related to torsors
Let
![]() ${\mathcal{G}}$
be a smooth affine group scheme over
${\mathcal{G}}$
be a smooth affine group scheme over
![]() $X$
, and
$X$
, and
![]() $E$
be a
$E$
be a
![]() ${\mathcal{G}}$
-torsor on
${\mathcal{G}}$
-torsor on
![]() $X$
. We denote by
$X$
. We denote by
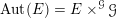 $\operatorname{Aut}(E)=E\times ^{{\mathcal{G}}}{\mathcal{G}}$
the adjoint torsor and
$\operatorname{Aut}(E)=E\times ^{{\mathcal{G}}}{\mathcal{G}}$
the adjoint torsor and
![]() $\operatorname{ad}(E)$
or
$\operatorname{ad}(E)$
or
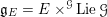 $\mathfrak{g}_{E}=E\times ^{{\mathcal{G}}}\operatorname{Lie}\,{\mathcal{G}}$
the adjoint bundle.
$\mathfrak{g}_{E}=E\times ^{{\mathcal{G}}}\operatorname{Lie}\,{\mathcal{G}}$
the adjoint bundle.
2 The Hitchin fibration
In this section, we review some basic geometric facts of Hitchin fibrations, following [Reference NgôNgô06, Reference NgôNgô10]. Only §2.7 is probably new.
2.1 Notations related to reductive groups
Let
![]() $G$
be a reductive algebraic group over
$G$
be a reductive algebraic group over
![]() $k$
of rank
$k$
of rank
![]() $l$
. We denote by
$l$
. We denote by
![]() $\breve{G}$
its Langlands dual group over
$\breve{G}$
its Langlands dual group over
![]() $k$
. We denote by
$k$
. We denote by
![]() $\mathfrak{g}$
(respectively by
$\mathfrak{g}$
(respectively by
![]() $\breve{\mathfrak{g}}$
) the Lie algebra of
$\breve{\mathfrak{g}}$
) the Lie algebra of
![]() $G$
(respectively
$G$
(respectively
![]() $\breve{G}$
). Let
$\breve{G}$
). Let
![]() $T$
denote the abstract Cartan of
$T$
denote the abstract Cartan of
![]() $G$
with its Lie algebra
$G$
with its Lie algebra
![]() $\mathfrak{t}$
. The counterparts on the Langlands dual side are denoted by
$\mathfrak{t}$
. The counterparts on the Langlands dual side are denoted by
![]() $\breve{T},\breve{\mathfrak{t}}$
. We denote by
$\breve{T},\breve{\mathfrak{t}}$
. We denote by
![]() $\text{W}$
the abstract Weyl group of
$\text{W}$
the abstract Weyl group of
![]() $G$
, which acts on
$G$
, which acts on
![]() $T$
and
$T$
and
![]() $\breve{T}$
. We denote by
$\breve{T}$
. We denote by
![]() $\mathbb{X}^{\bullet }(T)$
or simply by
$\mathbb{X}^{\bullet }(T)$
or simply by
![]() $\mathbb{X}^{\bullet }$
(respectively by
$\mathbb{X}^{\bullet }$
(respectively by
![]() $\mathbb{X}_{\bullet }(T)$
or simply by
$\mathbb{X}_{\bullet }(T)$
or simply by
![]() $\mathbb{X}_{\bullet }$
) the character (respectively the cocharacter) group of
$\mathbb{X}_{\bullet }$
) the character (respectively the cocharacter) group of
![]() $T$
. Let
$T$
. Let
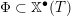 $\unicode[STIX]{x1D6F7}\subset \mathbb{X}^{\bullet }(T)$
be the set of roots. Sometimes, we also fix a set of simple roots
$\unicode[STIX]{x1D6F7}\subset \mathbb{X}^{\bullet }(T)$
be the set of roots. Sometimes, we also fix a set of simple roots
 $\{\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{l}\}$
and an embedding
$\{\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{l}\}$
and an embedding
![]() $\mathfrak{t}\subset \mathfrak{g}$
. Then for
$\mathfrak{t}\subset \mathfrak{g}$
. Then for
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}$
, let
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}$
, let
![]() $\mathfrak{g}_{\unicode[STIX]{x1D6FC}}\subset \mathfrak{g}$
denote the corresponding root subspace.
$\mathfrak{g}_{\unicode[STIX]{x1D6FC}}\subset \mathfrak{g}$
denote the corresponding root subspace.
From now on, we assume that the
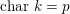 $\operatorname{char}~k=p$
is zero or
$\operatorname{char}~k=p$
is zero or
![]() $p\nmid |\text{W}|$
. We fix a
$p\nmid |\text{W}|$
. We fix a
![]() $\text{W}$
-invariant non-degenerate bilinear form
$\text{W}$
-invariant non-degenerate bilinear form
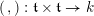 $(\,,\,):\mathfrak{t}\times \mathfrak{t}\rightarrow k$
and identify
$(\,,\,):\mathfrak{t}\times \mathfrak{t}\rightarrow k$
and identify
![]() $\mathfrak{t}$
with
$\mathfrak{t}$
with
![]() $\breve{\mathfrak{t}}$
using
$\breve{\mathfrak{t}}$
using
![]() $(\,,\,)$
. This invariant form also determines a unique
$(\,,\,)$
. This invariant form also determines a unique
![]() $G$
-invariant non-degenerate bilinear form
$G$
-invariant non-degenerate bilinear form
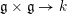 $\mathfrak{g}\times \mathfrak{g}\rightarrow k$
, still denoted by
$\mathfrak{g}\times \mathfrak{g}\rightarrow k$
, still denoted by
![]() $(\,,\,)$
. Let
$(\,,\,)$
. Let
![]() $\mathfrak{g}\simeq \mathfrak{g}^{\ast }$
be the resulting
$\mathfrak{g}\simeq \mathfrak{g}^{\ast }$
be the resulting
![]() $G$
-equivariant isomorphism.
$G$
-equivariant isomorphism.
2.2 Hitchin map
Let
![]() $k[\mathfrak{g}]$
and
$k[\mathfrak{g}]$
and
![]() $k[\mathfrak{t}]$
be the algebras of polynomial functions on
$k[\mathfrak{t}]$
be the algebras of polynomial functions on
![]() $\mathfrak{g}$
and on
$\mathfrak{g}$
and on
![]() $\mathfrak{t}$
respectively. By Chevalley’s theorem, we have an isomorphism
$\mathfrak{t}$
respectively. By Chevalley’s theorem, we have an isomorphism
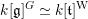 $k[\mathfrak{g}]^{G}\simeq k[\mathfrak{t}]^{\text{W}}$
. Moreover,
$k[\mathfrak{g}]^{G}\simeq k[\mathfrak{t}]^{\text{W}}$
. Moreover,
![]() $k[\mathfrak{t}]^{\text{W}}$
is isomorphic to a polynomial ring of
$k[\mathfrak{t}]^{\text{W}}$
is isomorphic to a polynomial ring of
![]() $l$
variables
$l$
variables
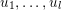 $u_{1},\ldots ,u_{l}$
and each
$u_{1},\ldots ,u_{l}$
and each
![]() $u_{i}$
is homogeneous in degree
$u_{i}$
is homogeneous in degree
![]() $e_{i}$
. Let
$e_{i}$
. Let
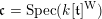 $\mathfrak{c}=\operatorname{Spec}(k[\mathfrak{t}]^{\text{W}})$
. The natural
$\mathfrak{c}=\operatorname{Spec}(k[\mathfrak{t}]^{\text{W}})$
. The natural
![]() $\mathbb{G}_{m}$
action on
$\mathbb{G}_{m}$
action on
![]() $\mathfrak{g}$
induces a
$\mathfrak{g}$
induces a
![]() $\mathbb{G}_{m}$
-action on
$\mathbb{G}_{m}$
-action on
![]() $\mathfrak{c}$
and under the isomorphism
$\mathfrak{c}$
and under the isomorphism
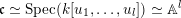 $\mathfrak{c}\simeq \operatorname{Spec}(k[u_{1},\ldots ,u_{l}])\simeq \mathbb{A}^{l}$
the action is given by
$\mathfrak{c}\simeq \operatorname{Spec}(k[u_{1},\ldots ,u_{l}])\simeq \mathbb{A}^{l}$
the action is given by
 $$\begin{eqnarray}h\cdot (a_{1},\ldots ,a_{l})=(h^{e_{1}}a_{1},\ldots ,h^{e_{l}}a_{l}).\end{eqnarray}$$
$$\begin{eqnarray}h\cdot (a_{1},\ldots ,a_{l})=(h^{e_{1}}a_{1},\ldots ,h^{e_{l}}a_{l}).\end{eqnarray}$$
Let
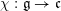 $\unicode[STIX]{x1D712}:\mathfrak{g}\rightarrow \mathfrak{c}$
be the map induced by
$\unicode[STIX]{x1D712}:\mathfrak{g}\rightarrow \mathfrak{c}$
be the map induced by
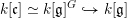 $k[\mathfrak{c}]\simeq k[\mathfrak{g}]^{G}{\hookrightarrow}k[\mathfrak{g}]$
. It is a
$k[\mathfrak{c}]\simeq k[\mathfrak{g}]^{G}{\hookrightarrow}k[\mathfrak{g}]$
. It is a
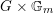 $G\times \mathbb{G}_{m}$
-equivariant map where
$G\times \mathbb{G}_{m}$
-equivariant map where
![]() $G$
acts trivially on
$G$
acts trivially on
![]() $\mathfrak{c}$
. Similarly, let
$\mathfrak{c}$
. Similarly, let
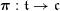 $\boldsymbol{\unicode[STIX]{x1D70B}}:\mathfrak{t}\rightarrow \mathfrak{c}$
be the map induced by
$\boldsymbol{\unicode[STIX]{x1D70B}}:\mathfrak{t}\rightarrow \mathfrak{c}$
be the map induced by
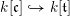 $k[\mathfrak{c}]{\hookrightarrow}k[\mathfrak{t}]$
, which is also
$k[\mathfrak{c}]{\hookrightarrow}k[\mathfrak{t}]$
, which is also
![]() $\mathbb{G}_{m}$
-equivariant. Let
$\mathbb{G}_{m}$
-equivariant. Let
![]() ${\mathcal{L}}$
be an invertible sheaf on
${\mathcal{L}}$
be an invertible sheaf on
![]() $C$
and
$C$
and
![]() ${\mathcal{L}}^{\times }$
be the corresponding
${\mathcal{L}}^{\times }$
be the corresponding
![]() $\mathbb{G}_{m}$
-torsor. We denote by
$\mathbb{G}_{m}$
-torsor. We denote by
 $\mathfrak{g}_{{\mathcal{L}}}=\mathfrak{g}\times ^{\mathbb{G}_{m}}{\mathcal{L}}^{\times }$
,
$\mathfrak{g}_{{\mathcal{L}}}=\mathfrak{g}\times ^{\mathbb{G}_{m}}{\mathcal{L}}^{\times }$
,
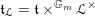 $\mathfrak{t}_{{\mathcal{L}}}=\mathfrak{t}\times ^{\mathbb{G}_{m}}{\mathcal{L}}^{\times }$
, and
$\mathfrak{t}_{{\mathcal{L}}}=\mathfrak{t}\times ^{\mathbb{G}_{m}}{\mathcal{L}}^{\times }$
, and
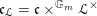 $\mathfrak{c}_{{\mathcal{L}}}=\mathfrak{c}\times ^{\mathbb{G}_{m}}{\mathcal{L}}^{\times }$
the
$\mathfrak{c}_{{\mathcal{L}}}=\mathfrak{c}\times ^{\mathbb{G}_{m}}{\mathcal{L}}^{\times }$
the
![]() $\mathbb{G}_{m}$
-twist of
$\mathbb{G}_{m}$
-twist of
![]() $\mathfrak{g}$
,
$\mathfrak{g}$
,
![]() $\mathfrak{t}$
, and
$\mathfrak{t}$
, and
![]() $\mathfrak{c}$
with respect to the natural
$\mathfrak{c}$
with respect to the natural
![]() $\mathbb{G}_{m}$
-action.
$\mathbb{G}_{m}$
-action.
Let
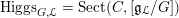 $\operatorname{Higgs}_{G,{\mathcal{L}}}=\operatorname{Sect}(C,[\mathfrak{g}_{{\mathcal{L}}}/G])$
be the stack of sections of
$\operatorname{Higgs}_{G,{\mathcal{L}}}=\operatorname{Sect}(C,[\mathfrak{g}_{{\mathcal{L}}}/G])$
be the stack of sections of
![]() $[\mathfrak{g}_{{\mathcal{L}}}/G]$
over
$[\mathfrak{g}_{{\mathcal{L}}}/G]$
over
![]() $C$
. That is, for each
$C$
. That is, for each
![]() $k$
-scheme
$k$
-scheme
![]() $S$
the groupoid
$S$
the groupoid
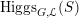 $\operatorname{Higgs}_{G,{\mathcal{L}}}(S)$
consist of maps
$\operatorname{Higgs}_{G,{\mathcal{L}}}(S)$
consist of maps
 $$\begin{eqnarray}h_{E,\unicode[STIX]{x1D719}}:C\times S\rightarrow [\mathfrak{g}_{{\mathcal{L}}}/G],\end{eqnarray}$$
$$\begin{eqnarray}h_{E,\unicode[STIX]{x1D719}}:C\times S\rightarrow [\mathfrak{g}_{{\mathcal{L}}}/G],\end{eqnarray}$$
or, equivalently, those maps
 $$\begin{eqnarray}h_{E,\unicode[STIX]{x1D719}}:C\times S\rightarrow [\mathfrak{g}/G\times \mathbb{G}_{m}]\end{eqnarray}$$
$$\begin{eqnarray}h_{E,\unicode[STIX]{x1D719}}:C\times S\rightarrow [\mathfrak{g}/G\times \mathbb{G}_{m}]\end{eqnarray}$$
such that the composition of
![]() $h_{E,\unicode[STIX]{x1D719}}$
with the projection
$h_{E,\unicode[STIX]{x1D719}}$
with the projection
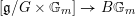 $[\mathfrak{g}/G\times \mathbb{G}_{m}]\rightarrow B\mathbb{G}_{m}$
is given by the
$[\mathfrak{g}/G\times \mathbb{G}_{m}]\rightarrow B\mathbb{G}_{m}$
is given by the
![]() $\mathbb{G}_{m}$
-torsor
$\mathbb{G}_{m}$
-torsor
![]() ${\mathcal{L}}^{\times }$
. Explicitly,
${\mathcal{L}}^{\times }$
. Explicitly,
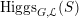 $\operatorname{Higgs}_{G,{\mathcal{L}}}(S)$
consist of pairs
$\operatorname{Higgs}_{G,{\mathcal{L}}}(S)$
consist of pairs
![]() $(E,\unicode[STIX]{x1D719})$
(called Higgs bundles), where
$(E,\unicode[STIX]{x1D719})$
(called Higgs bundles), where
![]() $E$
is an
$E$
is an
![]() $G$
-torsor over
$G$
-torsor over
![]() $C\times S$
and
$C\times S$
and
![]() $\unicode[STIX]{x1D719}$
is an element in
$\unicode[STIX]{x1D719}$
is an element in
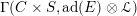 $\unicode[STIX]{x1D6E4}(C\times S,\operatorname{ad}(E)\otimes {\mathcal{L}})$
known as the Higgs field. If the group
$\unicode[STIX]{x1D6E4}(C\times S,\operatorname{ad}(E)\otimes {\mathcal{L}})$
known as the Higgs field. If the group
![]() $G$
is clear from the context, we simply write
$G$
is clear from the context, we simply write
![]() $\operatorname{Higgs}_{{\mathcal{L}}}$
for
$\operatorname{Higgs}_{{\mathcal{L}}}$
for
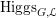 $\operatorname{Higgs}_{G,{\mathcal{L}}}$
.
$\operatorname{Higgs}_{G,{\mathcal{L}}}$
.
Let
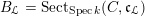 $B_{{\mathcal{L}}}=\operatorname{Sect}_{\operatorname{Spec}k}(C,\mathfrak{c}_{{\mathcal{L}}})$
be the scheme of sections of
$B_{{\mathcal{L}}}=\operatorname{Sect}_{\operatorname{Spec}k}(C,\mathfrak{c}_{{\mathcal{L}}})$
be the scheme of sections of
![]() $\mathfrak{c}_{{\mathcal{L}}}$
over
$\mathfrak{c}_{{\mathcal{L}}}$
over
![]() $C$
. That is, for each
$C$
. That is, for each
![]() $k$
-scheme
$k$
-scheme
![]() $S$
,
$S$
,
![]() $B_{{\mathcal{L}}}(S)$
is the set of sections
$B_{{\mathcal{L}}}(S)$
is the set of sections
 $$\begin{eqnarray}b:C\times S\rightarrow \mathfrak{c}_{{\mathcal{L}}},\end{eqnarray}$$
$$\begin{eqnarray}b:C\times S\rightarrow \mathfrak{c}_{{\mathcal{L}}},\end{eqnarray}$$
or, equivalently, those maps
 $$\begin{eqnarray}b:C\times S\rightarrow [\mathfrak{c}/\mathbb{G}_{m}]\end{eqnarray}$$
$$\begin{eqnarray}b:C\times S\rightarrow [\mathfrak{c}/\mathbb{G}_{m}]\end{eqnarray}$$
such that the composition of
![]() $b$
with the projection
$b$
with the projection
 $[\mathfrak{c}/\mathbb{G}_{m}]\rightarrow B\mathbb{G}_{m}$
is given by
$[\mathfrak{c}/\mathbb{G}_{m}]\rightarrow B\mathbb{G}_{m}$
is given by
![]() ${\mathcal{L}}^{\times }$
. It is called the Hitchin base of
${\mathcal{L}}^{\times }$
. It is called the Hitchin base of
![]() $G$
.
$G$
.
The natural
![]() $G$
-invariant projection
$G$
-invariant projection
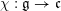 $\unicode[STIX]{x1D712}:\mathfrak{g}\rightarrow \mathfrak{c}$
induces a map
$\unicode[STIX]{x1D712}:\mathfrak{g}\rightarrow \mathfrak{c}$
induces a map
 $$\begin{eqnarray}[\unicode[STIX]{x1D712}_{{\mathcal{L}}}]:[\mathfrak{g}_{{\mathcal{L}}}/G]\rightarrow \mathfrak{c}_{{\mathcal{L}}},\end{eqnarray}$$
$$\begin{eqnarray}[\unicode[STIX]{x1D712}_{{\mathcal{L}}}]:[\mathfrak{g}_{{\mathcal{L}}}/G]\rightarrow \mathfrak{c}_{{\mathcal{L}}},\end{eqnarray}$$
or more generally
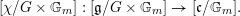 $$\begin{eqnarray}[\unicode[STIX]{x1D712}/G\times \mathbb{G}_{m}]:[\mathfrak{g}/G\times \mathbb{G}_{m}]\rightarrow [\mathfrak{c}/\mathbb{G}_{m}].\end{eqnarray}$$
$$\begin{eqnarray}[\unicode[STIX]{x1D712}/G\times \mathbb{G}_{m}]:[\mathfrak{g}/G\times \mathbb{G}_{m}]\rightarrow [\mathfrak{c}/\mathbb{G}_{m}].\end{eqnarray}$$
The map
![]() $[\unicode[STIX]{x1D712}_{{\mathcal{L}}}]$
induces a natural map
$[\unicode[STIX]{x1D712}_{{\mathcal{L}}}]$
induces a natural map
 $$\begin{eqnarray}h_{{\mathcal{L}}}:\operatorname{Higgs}_{{\mathcal{L}}}=\operatorname{Sect}(C,[\mathfrak{g}_{{\mathcal{L}}}/G])\rightarrow \operatorname{Sect}(C,\mathfrak{c}_{{\mathcal{L}}})=B_{{\mathcal{L}}}.\end{eqnarray}$$
$$\begin{eqnarray}h_{{\mathcal{L}}}:\operatorname{Higgs}_{{\mathcal{L}}}=\operatorname{Sect}(C,[\mathfrak{g}_{{\mathcal{L}}}/G])\rightarrow \operatorname{Sect}(C,\mathfrak{c}_{{\mathcal{L}}})=B_{{\mathcal{L}}}.\end{eqnarray}$$
Definition 2.2.1. We call
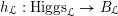 $h_{{\mathcal{L}}}:\operatorname{Higgs}_{{\mathcal{L}}}\rightarrow B_{{\mathcal{L}}}$
the Hitchin map associated to
$h_{{\mathcal{L}}}:\operatorname{Higgs}_{{\mathcal{L}}}\rightarrow B_{{\mathcal{L}}}$
the Hitchin map associated to
![]() ${\mathcal{L}}$
.
${\mathcal{L}}$
.
For any
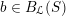 $b\in B_{{\mathcal{L}}}(S)$
we denote by
$b\in B_{{\mathcal{L}}}(S)$
we denote by
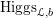 $\operatorname{Higgs}_{{\mathcal{L}},b}$
the fiber product
$\operatorname{Higgs}_{{\mathcal{L}},b}$
the fiber product
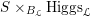 $S\times _{B_{{\mathcal{L}}}}\operatorname{Higgs}_{{\mathcal{L}}}$
.
$S\times _{B_{{\mathcal{L}}}}\operatorname{Higgs}_{{\mathcal{L}}}$
.
Observe that the invariant bilinear form
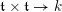 $\mathfrak{t}\times \mathfrak{t}\rightarrow k$
induces a canonical isomorphism
$\mathfrak{t}\times \mathfrak{t}\rightarrow k$
induces a canonical isomorphism
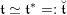 $\mathfrak{t}\simeq \mathfrak{t}^{\ast }=:\breve{\mathfrak{t}}$
, compatible with the
$\mathfrak{t}\simeq \mathfrak{t}^{\ast }=:\breve{\mathfrak{t}}$
, compatible with the
![]() $\text{W}$
-action. Therefore, there is a canonical isomorphism
$\text{W}$
-action. Therefore, there is a canonical isomorphism
![]() $\mathfrak{c}\simeq \breve{\mathfrak{c}}$
and
$\mathfrak{c}\simeq \breve{\mathfrak{c}}$
and
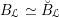 $B_{{\mathcal{L}}}\simeq \breve{B}_{{\mathcal{L}}}$
. In what follows, we will identify them.
$B_{{\mathcal{L}}}\simeq \breve{B}_{{\mathcal{L}}}$
. In what follows, we will identify them.
Let
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{C}$
be the canonical line bundle of
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{C}$
be the canonical line bundle of
![]() $C$
. We are mostly interested in the case
$C$
. We are mostly interested in the case
![]() ${\mathcal{L}}=\unicode[STIX]{x1D714}$
. For simplicity, from now on we denote
${\mathcal{L}}=\unicode[STIX]{x1D714}$
. For simplicity, from now on we denote
 $B=B_{\unicode[STIX]{x1D714}}$
,
$B=B_{\unicode[STIX]{x1D714}}$
,
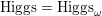 $\operatorname{Higgs}=\operatorname{Higgs}_{\unicode[STIX]{x1D714}}$
,
$\operatorname{Higgs}=\operatorname{Higgs}_{\unicode[STIX]{x1D714}}$
,
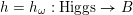 $h=h_{\unicode[STIX]{x1D714}}:\operatorname{Higgs}\rightarrow B$
, and
$h=h_{\unicode[STIX]{x1D714}}:\operatorname{Higgs}\rightarrow B$
, and
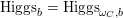 $\operatorname{Higgs}_{b}=\operatorname{Higgs}_{\unicode[STIX]{x1D714}_{C},b}$
. We sometimes also write
$\operatorname{Higgs}_{b}=\operatorname{Higgs}_{\unicode[STIX]{x1D714}_{C},b}$
. We sometimes also write
![]() $\operatorname{Higgs}_{G}$
for
$\operatorname{Higgs}_{G}$
for
![]() $\operatorname{Higgs}$
to emphasize the group
$\operatorname{Higgs}$
to emphasize the group
![]() $G$
. Observe that the bilinear form as in §2.1 together with the Serre duality induces an isomorphism
$G$
. Observe that the bilinear form as in §2.1 together with the Serre duality induces an isomorphism
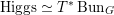 $\operatorname{Higgs}\simeq T^{\ast }\operatorname{Bun}_{G}$
(cf. [Reference HitchinHit87]).
$\operatorname{Higgs}\simeq T^{\ast }\operatorname{Bun}_{G}$
(cf. [Reference HitchinHit87]).
2.3 The Kostant section
In this section, we recall the construction of the Kostant section of the Hitchin map
![]() $h_{{\mathcal{L}}}$
. For each simple root
$h_{{\mathcal{L}}}$
. For each simple root
![]() $\unicode[STIX]{x1D6FC}_{i}$
we choose a non-zero vector
$\unicode[STIX]{x1D6FC}_{i}$
we choose a non-zero vector
 $f_{i}\in \mathfrak{g}_{-\unicode[STIX]{x1D6FC}_{i}}$
. Let
$f_{i}\in \mathfrak{g}_{-\unicode[STIX]{x1D6FC}_{i}}$
. Let
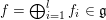 $f=\bigoplus _{i=1}^{l}f_{i}\in \mathfrak{g}$
. We complete
$f=\bigoplus _{i=1}^{l}f_{i}\in \mathfrak{g}$
. We complete
![]() $f$
into an
$f$
into an
![]() $\mathfrak{s}\mathfrak{l}_{2}$
triple
$\mathfrak{s}\mathfrak{l}_{2}$
triple
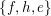 $\{f,h,e\}$
and denote by
$\{f,h,e\}$
and denote by
![]() $\mathfrak{g}^{e}$
the centralizer of
$\mathfrak{g}^{e}$
the centralizer of
![]() $e$
in
$e$
in
![]() $\mathfrak{g}$
. A theorem of Kostant says that
$\mathfrak{g}$
. A theorem of Kostant says that
![]() $f+\mathfrak{g}^{e}$
consist of regular elements in
$f+\mathfrak{g}^{e}$
consist of regular elements in
![]() $\mathfrak{g}$
and the restriction of
$\mathfrak{g}$
and the restriction of
 $\unicode[STIX]{x1D712}:\mathfrak{g}\rightarrow \mathfrak{c}$
to
$\unicode[STIX]{x1D712}:\mathfrak{g}\rightarrow \mathfrak{c}$
to
![]() $f+\mathfrak{g}^{e}$
is an isomorphism onto
$f+\mathfrak{g}^{e}$
is an isomorphism onto
![]() $\mathfrak{c}$
. We denote by
$\mathfrak{c}$
. We denote by
 $$\begin{eqnarray}\text{kos}:\mathfrak{c}\simeq f+\mathfrak{g}^{e}\end{eqnarray}$$
$$\begin{eqnarray}\text{kos}:\mathfrak{c}\simeq f+\mathfrak{g}^{e}\end{eqnarray}$$
the inverse of
![]() $\unicode[STIX]{x1D712}|_{f+\mathfrak{g}^{e}}$
. Let
$\unicode[STIX]{x1D712}|_{f+\mathfrak{g}^{e}}$
. Let
![]() $\unicode[STIX]{x1D70C}(\mathbb{G}_{m})$
denote the following
$\unicode[STIX]{x1D70C}(\mathbb{G}_{m})$
denote the following
![]() $\mathbb{G}_{m}$
-action on
$\mathbb{G}_{m}$
-action on
![]() $\mathfrak{g}$
: it acts trivially on
$\mathfrak{g}$
: it acts trivially on
![]() $\mathfrak{t}$
, and on
$\mathfrak{t}$
, and on
![]() $\mathfrak{g}_{\unicode[STIX]{x1D6FC}}$
by
$\mathfrak{g}_{\unicode[STIX]{x1D6FC}}$
by
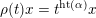 $\unicode[STIX]{x1D70C}(t)x=t^{\operatorname{ht}(\unicode[STIX]{x1D6FC})}x$
where
$\unicode[STIX]{x1D70C}(t)x=t^{\operatorname{ht}(\unicode[STIX]{x1D6FC})}x$
where
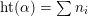 $\operatorname{ht}(\unicode[STIX]{x1D6FC})=\sum n_{i}$
if
$\operatorname{ht}(\unicode[STIX]{x1D6FC})=\sum n_{i}$
if
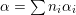 $\unicode[STIX]{x1D6FC}=\sum n_{i}\unicode[STIX]{x1D6FC}_{i}$
. We have
$\unicode[STIX]{x1D6FC}=\sum n_{i}\unicode[STIX]{x1D6FC}_{i}$
. We have
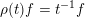 $\unicode[STIX]{x1D70C}(t)f=t^{-1}f$
and
$\unicode[STIX]{x1D70C}(t)f=t^{-1}f$
and
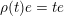 $\unicode[STIX]{x1D70C}(t)e=te$
, in particular
$\unicode[STIX]{x1D70C}(t)e=te$
, in particular
![]() $\mathfrak{g}^{e}$
is invariant under
$\mathfrak{g}^{e}$
is invariant under
![]() $\unicode[STIX]{x1D70C}(\mathbb{G}_{m})$
. We define a new
$\unicode[STIX]{x1D70C}(\mathbb{G}_{m})$
. We define a new
![]() $\mathbb{G}_{m}$
-action on
$\mathbb{G}_{m}$
-action on
![]() $\mathfrak{g}$
by
$\mathfrak{g}$
by
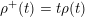 $\unicode[STIX]{x1D70C}^{+}(t)=t\unicode[STIX]{x1D70C}(t)$
. Then
$\unicode[STIX]{x1D70C}^{+}(t)=t\unicode[STIX]{x1D70C}(t)$
. Then
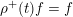 $\unicode[STIX]{x1D70C}^{+}(t)f=f$
and
$\unicode[STIX]{x1D70C}^{+}(t)f=f$
and
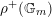 $\unicode[STIX]{x1D70C}^{+}(\mathbb{G}_{m})$
preserves
$\unicode[STIX]{x1D70C}^{+}(\mathbb{G}_{m})$
preserves
![]() $f+\mathfrak{g}^{e}$
. With respect to this action, the isomorphism
$f+\mathfrak{g}^{e}$
. With respect to this action, the isomorphism
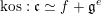 $\text{kos}:\mathfrak{c}\simeq f+\mathfrak{g}^{e}$
is
$\text{kos}:\mathfrak{c}\simeq f+\mathfrak{g}^{e}$
is
![]() $\mathbb{G}_{m}$
-equivariant.
$\mathbb{G}_{m}$
-equivariant.
The diagonal map
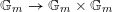 $\mathbb{G}_{m}\rightarrow \mathbb{G}_{m}\times \mathbb{G}_{m}$
induces a map
$\mathbb{G}_{m}\rightarrow \mathbb{G}_{m}\times \mathbb{G}_{m}$
induces a map
 $$\begin{eqnarray}[\mathfrak{g}/\unicode[STIX]{x1D70C}^{+}(\mathbb{G}_{m})]\rightarrow [\mathfrak{g}/\mathbb{G}_{m}\times \unicode[STIX]{x1D70C}(\mathbb{G}_{m})].\end{eqnarray}$$
$$\begin{eqnarray}[\mathfrak{g}/\unicode[STIX]{x1D70C}^{+}(\mathbb{G}_{m})]\rightarrow [\mathfrak{g}/\mathbb{G}_{m}\times \unicode[STIX]{x1D70C}(\mathbb{G}_{m})].\end{eqnarray}$$
By precomposing with the map
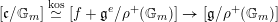 $[\mathfrak{c}/\mathbb{G}_{m}]\stackrel{\text{kos}}{\simeq }[f+\mathfrak{g}^{e}/\unicode[STIX]{x1D70C}^{+}(\mathbb{G}_{m})]\rightarrow [\mathfrak{g}/\unicode[STIX]{x1D70C}^{+}(\mathbb{G}_{m})]$
we obtain
$[\mathfrak{c}/\mathbb{G}_{m}]\stackrel{\text{kos}}{\simeq }[f+\mathfrak{g}^{e}/\unicode[STIX]{x1D70C}^{+}(\mathbb{G}_{m})]\rightarrow [\mathfrak{g}/\unicode[STIX]{x1D70C}^{+}(\mathbb{G}_{m})]$
we obtain
 $$\begin{eqnarray}[\mathfrak{c}/\mathbb{G}_{m}]\rightarrow [\mathfrak{g}/\mathbb{G}_{m}\times \unicode[STIX]{x1D70C}(\mathbb{G}_{m})].\end{eqnarray}$$
$$\begin{eqnarray}[\mathfrak{c}/\mathbb{G}_{m}]\rightarrow [\mathfrak{g}/\mathbb{G}_{m}\times \unicode[STIX]{x1D70C}(\mathbb{G}_{m})].\end{eqnarray}$$
If the action of
![]() $\unicode[STIX]{x1D70C}(\mathbb{G}_{m})$
on
$\unicode[STIX]{x1D70C}(\mathbb{G}_{m})$
on
![]() $\mathfrak{g}$
factors through the adjoint action of
$\mathfrak{g}$
factors through the adjoint action of
![]() $G$
, for example when
$G$
, for example when
![]() $G$
is adjoint, then there is a map
$G$
is adjoint, then there is a map
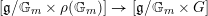 $[\mathfrak{g}/\mathbb{G}_{m}\times \unicode[STIX]{x1D70C}(\mathbb{G}_{m})]\rightarrow [\mathfrak{g}/\mathbb{G}_{m}\times G]$
which defines a section
$[\mathfrak{g}/\mathbb{G}_{m}\times \unicode[STIX]{x1D70C}(\mathbb{G}_{m})]\rightarrow [\mathfrak{g}/\mathbb{G}_{m}\times G]$
which defines a section
 $$\begin{eqnarray}[\mathfrak{c}/\mathbb{G}_{m}]\rightarrow [\mathfrak{g}/\mathbb{G}_{m}\times \unicode[STIX]{x1D70C}(\mathbb{G}_{m})]\rightarrow [\mathfrak{g}/\mathbb{G}_{m}\times G]\end{eqnarray}$$
$$\begin{eqnarray}[\mathfrak{c}/\mathbb{G}_{m}]\rightarrow [\mathfrak{g}/\mathbb{G}_{m}\times \unicode[STIX]{x1D70C}(\mathbb{G}_{m})]\rightarrow [\mathfrak{g}/\mathbb{G}_{m}\times G]\end{eqnarray}$$
of (2.2.1), and in particular, we get a section of
![]() $h_{{\mathcal{L}}}$
. In general, the action
$h_{{\mathcal{L}}}$
. In general, the action
![]() $\unicode[STIX]{x1D70C}(\mathbb{G}_{m})$
does not necessarily factor through
$\unicode[STIX]{x1D70C}(\mathbb{G}_{m})$
does not necessarily factor through
![]() $G$
, but its square does since it is given by the cocharacter
$G$
, but its square does since it is given by the cocharacter
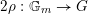 $2\unicode[STIX]{x1D70C}:\mathbb{G}_{m}\rightarrow G$
where
$2\unicode[STIX]{x1D70C}:\mathbb{G}_{m}\rightarrow G$
where
![]() $2\unicode[STIX]{x1D70C}$
is the sum of positive coroots. So if we denote
$2\unicode[STIX]{x1D70C}$
is the sum of positive coroots. So if we denote
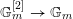 $\mathbb{G}_{m}^{[2]}\rightarrow \mathbb{G}_{m}$
the square map (so
$\mathbb{G}_{m}^{[2]}\rightarrow \mathbb{G}_{m}$
the square map (so
![]() $\mathbb{G}_{m}^{[2]}$
is isomorphic to
$\mathbb{G}_{m}^{[2]}$
is isomorphic to
![]() $\mathbb{G}_{m}$
, but regarded as its the double cover), we get a map
$\mathbb{G}_{m}$
, but regarded as its the double cover), we get a map
 $$\begin{eqnarray}\unicode[STIX]{x1D702}^{1/2}:[\mathfrak{c}/\mathbb{G}_{m}^{[2]}]\rightarrow [\mathfrak{g}/\mathbb{G}_{m}^{[2]}\times \unicode[STIX]{x1D70C}(\mathbb{G}_{m}^{[2]})]\rightarrow [\mathfrak{g}/\mathbb{G}_{m}^{[2]}\times G].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D702}^{1/2}:[\mathfrak{c}/\mathbb{G}_{m}^{[2]}]\rightarrow [\mathfrak{g}/\mathbb{G}_{m}^{[2]}\times \unicode[STIX]{x1D70C}(\mathbb{G}_{m}^{[2]})]\rightarrow [\mathfrak{g}/\mathbb{G}_{m}^{[2]}\times G].\end{eqnarray}$$
Let
![]() ${\mathcal{L}}^{1/2}$
be a square root of
${\mathcal{L}}^{1/2}$
be a square root of
![]() ${\mathcal{L}}$
. Then every
${\mathcal{L}}$
. Then every
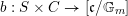 $b:S\times C\rightarrow [\mathfrak{c}/\mathbb{G}_{m}]$
in
$b:S\times C\rightarrow [\mathfrak{c}/\mathbb{G}_{m}]$
in
![]() $B_{{\mathcal{L}}}(S)$
factors through a unique map
$B_{{\mathcal{L}}}(S)$
factors through a unique map
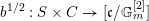 $b^{1/2}:S\times C\rightarrow [\mathfrak{c}/\mathbb{G}_{m}^{[2]}]$
. Therefore, by composing with
$b^{1/2}:S\times C\rightarrow [\mathfrak{c}/\mathbb{G}_{m}^{[2]}]$
. Therefore, by composing with
![]() $\unicode[STIX]{x1D702}^{1/2}$
, we get a lift of
$\unicode[STIX]{x1D702}^{1/2}$
, we get a lift of
![]() $b$
:
$b$
:
 $$\begin{eqnarray}\unicode[STIX]{x1D702}^{1/2}(b):S\times C\stackrel{b^{1/2}}{\longrightarrow }[\mathfrak{c}/\mathbb{G}_{m}^{[2]}]\stackrel{\unicode[STIX]{x1D702}^{1/2}}{\longrightarrow }[\mathfrak{g}/\mathbb{G}_{m}^{[2]}\times G]\rightarrow [\mathfrak{g}/\mathbb{G}_{m}\times G].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D702}^{1/2}(b):S\times C\stackrel{b^{1/2}}{\longrightarrow }[\mathfrak{c}/\mathbb{G}_{m}^{[2]}]\stackrel{\unicode[STIX]{x1D702}^{1/2}}{\longrightarrow }[\mathfrak{g}/\mathbb{G}_{m}^{[2]}\times G]\rightarrow [\mathfrak{g}/\mathbb{G}_{m}\times G].\end{eqnarray}$$
The assignment
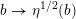 $b\rightarrow \unicode[STIX]{x1D702}^{1/2}(b)$
defines a section
$b\rightarrow \unicode[STIX]{x1D702}^{1/2}(b)$
defines a section
 $$\begin{eqnarray}\unicode[STIX]{x1D702}_{{\mathcal{L}}^{1/2}}:B_{{\mathcal{L}}}\rightarrow \operatorname{Higgs}_{{\mathcal{L}}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D702}_{{\mathcal{L}}^{1/2}}:B_{{\mathcal{L}}}\rightarrow \operatorname{Higgs}_{{\mathcal{L}}}\end{eqnarray}$$
of the Hitchin map
![]() $h_{{\mathcal{L}}}$
.
$h_{{\mathcal{L}}}$
.
We fix a square root
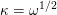 $\unicode[STIX]{x1D705}=\unicode[STIX]{x1D714}^{1/2}$
(called a theta characteristic) of
$\unicode[STIX]{x1D705}=\unicode[STIX]{x1D714}^{1/2}$
(called a theta characteristic) of
![]() $\unicode[STIX]{x1D714}$
and write
$\unicode[STIX]{x1D714}$
and write
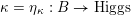 $\unicode[STIX]{x1D705}=\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D705}}:B\rightarrow \operatorname{Higgs}$
.
$\unicode[STIX]{x1D705}=\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D705}}:B\rightarrow \operatorname{Higgs}$
.
2.4 Cameral curve
For any
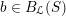 $b\in B_{{\mathcal{L}}}(S)$
, the cameral curve
$b\in B_{{\mathcal{L}}}(S)$
, the cameral curve
![]() $\widetilde{C}_{b}$
is defined as the fiber product, as follows.
$\widetilde{C}_{b}$
is defined as the fiber product, as follows.

When
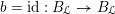 $b=\operatorname{id}:B_{{\mathcal{L}}}\rightarrow B_{{\mathcal{L}}}$
, the corresponding cameral curve
$b=\operatorname{id}:B_{{\mathcal{L}}}\rightarrow B_{{\mathcal{L}}}$
, the corresponding cameral curve
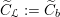 $\widetilde{C}_{{\mathcal{L}}}:=\widetilde{C}_{b}$
is called the universal cameral curve. For simplicity, we will write
$\widetilde{C}_{{\mathcal{L}}}:=\widetilde{C}_{b}$
is called the universal cameral curve. For simplicity, we will write
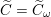 $\widetilde{C}=\widetilde{C}_{\unicode[STIX]{x1D714}}$
,
$\widetilde{C}=\widetilde{C}_{\unicode[STIX]{x1D714}}$
,
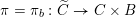 $\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{b}:\widetilde{C}\rightarrow C\times B$
.
$\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{b}:\widetilde{C}\rightarrow C\times B$
.
2.5 The universal centralizer group schemes
Consider the group scheme
![]() $I$
over
$I$
over
![]() $\mathfrak{g}$
consisting of pairs
$\mathfrak{g}$
consisting of pairs
 $$\begin{eqnarray}I=\{(g,x)\in G\times \mathfrak{g}\mid \operatorname{Ad}_{g}(x)=x\}.\end{eqnarray}$$
$$\begin{eqnarray}I=\{(g,x)\in G\times \mathfrak{g}\mid \operatorname{Ad}_{g}(x)=x\}.\end{eqnarray}$$
We define
 $J=\text{kos}^{\ast }I$
, where
$J=\text{kos}^{\ast }I$
, where
 $\text{kos}:\mathfrak{c}\rightarrow \mathfrak{g}$
is the Kostant section. This is called the universal centralizer group scheme of
$\text{kos}:\mathfrak{c}\rightarrow \mathfrak{g}$
is the Kostant section. This is called the universal centralizer group scheme of
![]() $\mathfrak{g}$
(see Proposition 2.5.1). To study it, it is convenient to introduce two auxiliary group schemes. We define
$\mathfrak{g}$
(see Proposition 2.5.1). To study it, it is convenient to introduce two auxiliary group schemes. We define
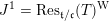 $J^{1}=\operatorname{Res}_{\mathfrak{t}/\mathfrak{c}}(T)^{\text{W}}$
and let
$J^{1}=\operatorname{Res}_{\mathfrak{t}/\mathfrak{c}}(T)^{\text{W}}$
and let
![]() $J^{0}$
to be the neutral component of
$J^{0}$
to be the neutral component of
![]() $J^{1}$
. All the group schemes
$J^{1}$
. All the group schemes
![]() $J$
,
$J$
,
![]() $J^{0}$
and
$J^{0}$
and
![]() $J^{1}$
are smooth commutative group schemes over
$J^{1}$
are smooth commutative group schemes over
![]() $\mathfrak{c}$
. The following proposition is proved in [Reference NgôNgô06] (see also [Reference Donagi and GaitsgoryDG02]).
$\mathfrak{c}$
. The following proposition is proved in [Reference NgôNgô06] (see also [Reference Donagi and GaitsgoryDG02]).
Proposition 2.5.1.
-
(1) There is a unique morphism of group schemes
 $a:\unicode[STIX]{x1D712}^{\ast }J\rightarrow I\subset G\times \mathfrak{g}$
, which extends the canonical isomorphism
$a:\unicode[STIX]{x1D712}^{\ast }J\rightarrow I\subset G\times \mathfrak{g}$
, which extends the canonical isomorphism
 $\unicode[STIX]{x1D712}^{\ast }J|_{\mathfrak{g}^{\text{reg}}}\simeq I|_{\mathfrak{g}^{\text{reg}}}$
.
$\unicode[STIX]{x1D712}^{\ast }J|_{\mathfrak{g}^{\text{reg}}}\simeq I|_{\mathfrak{g}^{\text{reg}}}$
. -
(2) There are natural inclusions
 $J^{0}\subset J\subset J^{1}$
.
$J^{0}\subset J\subset J^{1}$
. -
(3) The inclusion
 $J\subset J^{1}=\operatorname{Res}_{\mathfrak{t}/\mathfrak{c}}(T)^{\text{W}}$
in part (2) defines a morphism of group schemes over
$J\subset J^{1}=\operatorname{Res}_{\mathfrak{t}/\mathfrak{c}}(T)^{\text{W}}$
in part (2) defines a morphism of group schemes over $$\begin{eqnarray}\text{j}^{1}:\boldsymbol{\unicode[STIX]{x1D70B}}^{\ast }J\rightarrow T\times \mathfrak{t}\end{eqnarray}$$
$$\begin{eqnarray}\text{j}^{1}:\boldsymbol{\unicode[STIX]{x1D70B}}^{\ast }J\rightarrow T\times \mathfrak{t}\end{eqnarray}$$
 $\mathfrak{t}$
, which is an isomorphism over
$\mathfrak{t}$
, which is an isomorphism over
 $\mathfrak{t}^{rs}$
.
$\mathfrak{t}^{rs}$
.
All the above constructions can be twisted. Namely, there are
![]() $\mathbb{G}_{m}$
-actions on
$\mathbb{G}_{m}$
-actions on
![]() $I$
,
$I$
,
![]() $J$
,
$J$
,
![]() $J^{1}$
and
$J^{1}$
and
![]() $J^{0}$
. Moreover, the
$J^{0}$
. Moreover, the
![]() $\mathbb{G}_{m}$
-action on
$\mathbb{G}_{m}$
-action on
![]() $I$
can be extended to a
$I$
can be extended to a
 $G\times \mathbb{G}_{m}$
-action given by
$G\times \mathbb{G}_{m}$
-action given by
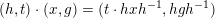 $(h,t)\cdot (x,g)=(t\cdot hxh^{-1},hgh^{-1})$
. The natural morphisms
$(h,t)\cdot (x,g)=(t\cdot hxh^{-1},hgh^{-1})$
. The natural morphisms
![]() $J\rightarrow \mathfrak{c}$
and
$J\rightarrow \mathfrak{c}$
and
![]() $I\rightarrow \mathfrak{g}$
are
$I\rightarrow \mathfrak{g}$
are
![]() $\mathbb{G}_{m}$
-equivariant, and therefore we can twist everything by the
$\mathbb{G}_{m}$
-equivariant, and therefore we can twist everything by the
![]() $\mathbb{G}_{m}$
-torsor
$\mathbb{G}_{m}$
-torsor
![]() ${\mathcal{L}}^{\times }$
to get
${\mathcal{L}}^{\times }$
to get
 $J_{{\mathcal{L}}}\rightarrow \mathfrak{c}_{{\mathcal{L}}}$
,
$J_{{\mathcal{L}}}\rightarrow \mathfrak{c}_{{\mathcal{L}}}$
,
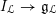 $I_{{\mathcal{L}}}\rightarrow \mathfrak{g}_{{\mathcal{L}}}$
where
$I_{{\mathcal{L}}}\rightarrow \mathfrak{g}_{{\mathcal{L}}}$
where
 $J_{{\mathcal{L}}}=J\times ^{\mathbb{G}_{m}}{\mathcal{L}}^{\times }$
and
$J_{{\mathcal{L}}}=J\times ^{\mathbb{G}_{m}}{\mathcal{L}}^{\times }$
and
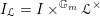 $I_{{\mathcal{L}}}=I\times ^{\mathbb{G}_{m}}{\mathcal{L}}^{\times }$
. Similarly, we have
$I_{{\mathcal{L}}}=I\times ^{\mathbb{G}_{m}}{\mathcal{L}}^{\times }$
. Similarly, we have
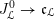 $J_{{\mathcal{L}}}^{0}\rightarrow \mathfrak{c}_{{\mathcal{L}}}$
and
$J_{{\mathcal{L}}}^{0}\rightarrow \mathfrak{c}_{{\mathcal{L}}}$
and
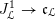 $J_{{\mathcal{L}}}^{1}\rightarrow \mathfrak{c}_{{\mathcal{L}}}$
, and there are natural inclusions
$J_{{\mathcal{L}}}^{1}\rightarrow \mathfrak{c}_{{\mathcal{L}}}$
, and there are natural inclusions
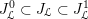 $J_{{\mathcal{L}}}^{0}\subset J_{{\mathcal{L}}}\subset J_{{\mathcal{L}}}^{1}$
. The group scheme
$J_{{\mathcal{L}}}^{0}\subset J_{{\mathcal{L}}}\subset J_{{\mathcal{L}}}^{1}$
. The group scheme
![]() $I_{{\mathcal{L}}}$
over
$I_{{\mathcal{L}}}$
over
![]() $\mathfrak{g}_{{\mathcal{L}}}$
is equivariant under the
$\mathfrak{g}_{{\mathcal{L}}}$
is equivariant under the
![]() $G$
-action, hence it descends to a group scheme
$G$
-action, hence it descends to a group scheme
![]() $[I_{{\mathcal{L}}}]$
over
$[I_{{\mathcal{L}}}]$
over
![]() $[\mathfrak{g}_{{\mathcal{L}}}/G]$
.
$[\mathfrak{g}_{{\mathcal{L}}}/G]$
.
2.6 Symmetries of Hitchin fibration
Let
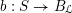 $b:S\rightarrow B_{{\mathcal{L}}}$
be an
$b:S\rightarrow B_{{\mathcal{L}}}$
be an
![]() $S$
-point of
$S$
-point of
![]() $B_{{\mathcal{L}}}$
, corresponding to a map
$B_{{\mathcal{L}}}$
, corresponding to a map
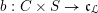 $b:C\times S\rightarrow \mathfrak{c}_{{\mathcal{L}}}$
. Pulling back
$b:C\times S\rightarrow \mathfrak{c}_{{\mathcal{L}}}$
. Pulling back
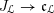 $J_{{\mathcal{L}}}\rightarrow \mathfrak{c}_{{\mathcal{L}}}$
along this map, we obtain a smooth group scheme
$J_{{\mathcal{L}}}\rightarrow \mathfrak{c}_{{\mathcal{L}}}$
along this map, we obtain a smooth group scheme
 $J_{b}=b^{\ast }J$
over
$J_{b}=b^{\ast }J$
over
![]() $C\times S$
.
$C\times S$
.
Let
![]() $\mathscr{P}_{b}$
be the Picard category of
$\mathscr{P}_{b}$
be the Picard category of
![]() $J_{b}$
-torsors over
$J_{b}$
-torsors over
![]() $C\times S$
. The assignment
$C\times S$
. The assignment
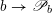 $b\rightarrow \mathscr{P}_{b}$
defines a Picard stack over
$b\rightarrow \mathscr{P}_{b}$
defines a Picard stack over
![]() $B$
, denoted by
$B$
, denoted by
![]() $\mathscr{P}_{{\mathcal{L}}}$
. Let us fix
$\mathscr{P}_{{\mathcal{L}}}$
. Let us fix
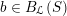 $b\in B_{{\mathcal{L}}}(S)$
, and let
$b\in B_{{\mathcal{L}}}(S)$
, and let
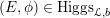 $(E,\unicode[STIX]{x1D719})\in \operatorname{Higgs}_{{\mathcal{L}},b}$
corresponding to the map
$(E,\unicode[STIX]{x1D719})\in \operatorname{Higgs}_{{\mathcal{L}},b}$
corresponding to the map
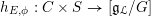 $h_{E,\unicode[STIX]{x1D719}}:C\times S\rightarrow [\mathfrak{g}_{{\mathcal{L}}}/G]$
. Observe that the morphism
$h_{E,\unicode[STIX]{x1D719}}:C\times S\rightarrow [\mathfrak{g}_{{\mathcal{L}}}/G]$
. Observe that the morphism
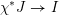 $\unicode[STIX]{x1D712}^{\ast }J\rightarrow I$
in Proposition 2.5.1 induces
$\unicode[STIX]{x1D712}^{\ast }J\rightarrow I$
in Proposition 2.5.1 induces
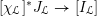 $[\unicode[STIX]{x1D712}_{{\mathcal{L}}}]^{\ast }J_{{\mathcal{L}}}\rightarrow [I_{{\mathcal{L}}}]$
of group schemes over
$[\unicode[STIX]{x1D712}_{{\mathcal{L}}}]^{\ast }J_{{\mathcal{L}}}\rightarrow [I_{{\mathcal{L}}}]$
of group schemes over
![]() $[\mathfrak{g}_{{\mathcal{L}}}/G]$
. Pulling back to
$[\mathfrak{g}_{{\mathcal{L}}}/G]$
. Pulling back to
![]() $C\times S$
using
$C\times S$
using
![]() $h_{E,\unicode[STIX]{x1D719}}$
, we get a map
$h_{E,\unicode[STIX]{x1D719}}$
, we get a map
 $$\begin{eqnarray}a_{E,\unicode[STIX]{x1D719}}:J_{b}\rightarrow h_{E,\unicode[STIX]{x1D719}}^{\ast }[I]=\operatorname{Aut}(E,\unicode[STIX]{x1D719})\subset \operatorname{Aut}(E),\end{eqnarray}$$
$$\begin{eqnarray}a_{E,\unicode[STIX]{x1D719}}:J_{b}\rightarrow h_{E,\unicode[STIX]{x1D719}}^{\ast }[I]=\operatorname{Aut}(E,\unicode[STIX]{x1D719})\subset \operatorname{Aut}(E),\end{eqnarray}$$
which allows us to twist
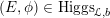 $(E,\unicode[STIX]{x1D719})\in \operatorname{Higgs}_{{\mathcal{L}},b}$
by a
$(E,\unicode[STIX]{x1D719})\in \operatorname{Higgs}_{{\mathcal{L}},b}$
by a
![]() $J_{b}$
-torsor. This construction defines an action of
$J_{b}$
-torsor. This construction defines an action of
![]() $\mathscr{P}_{{\mathcal{L}}}$
on
$\mathscr{P}_{{\mathcal{L}}}$
on
![]() $\operatorname{Higgs}_{{\mathcal{L}}}$
over
$\operatorname{Higgs}_{{\mathcal{L}}}$
over
![]() $B_{{\mathcal{L}}}$
.
$B_{{\mathcal{L}}}$
.
Let
 $\operatorname{Higgs}_{{\mathcal{L}}}^{\text{reg}}$
be the open stack of
$\operatorname{Higgs}_{{\mathcal{L}}}^{\text{reg}}$
be the open stack of
![]() $\operatorname{Higgs}_{{\mathcal{L}}}$
consisting of
$\operatorname{Higgs}_{{\mathcal{L}}}$
consisting of
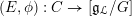 $(E,\unicode[STIX]{x1D719}):C\rightarrow [\mathfrak{g}_{{\mathcal{L}}}/G]$
that factors through
$(E,\unicode[STIX]{x1D719}):C\rightarrow [\mathfrak{g}_{{\mathcal{L}}}/G]$
that factors through
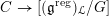 $C\rightarrow [(\mathfrak{g}^{\text{reg}})_{{\mathcal{L}}}/G]$
. If
$C\rightarrow [(\mathfrak{g}^{\text{reg}})_{{\mathcal{L}}}/G]$
. If
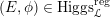 $(E,\unicode[STIX]{x1D719})\in \operatorname{Higgs}_{{\mathcal{L}}}^{\text{reg}}$
, then
$(E,\unicode[STIX]{x1D719})\in \operatorname{Higgs}_{{\mathcal{L}}}^{\text{reg}}$
, then
![]() $a_{E,\unicode[STIX]{x1D719}}$
above is an isomorphism. The Kostant section
$a_{E,\unicode[STIX]{x1D719}}$
above is an isomorphism. The Kostant section
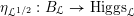 $\unicode[STIX]{x1D702}_{{\mathcal{L}}^{1/2}}:B_{{\mathcal{L}}}\rightarrow \operatorname{Higgs}_{{\mathcal{L}}}$
factors through
$\unicode[STIX]{x1D702}_{{\mathcal{L}}^{1/2}}:B_{{\mathcal{L}}}\rightarrow \operatorname{Higgs}_{{\mathcal{L}}}$
factors through
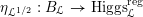 $\unicode[STIX]{x1D702}_{{\mathcal{L}}^{1/2}}:B_{{\mathcal{L}}}\rightarrow \operatorname{Higgs}_{{\mathcal{L}}}^{\text{reg}}$
. Following [Reference NgôNgô06, §4], we define
$\unicode[STIX]{x1D702}_{{\mathcal{L}}^{1/2}}:B_{{\mathcal{L}}}\rightarrow \operatorname{Higgs}_{{\mathcal{L}}}^{\text{reg}}$
. Following [Reference NgôNgô06, §4], we define
![]() $B_{{\mathcal{L}}}^{0}$
as the open sub-scheme of
$B_{{\mathcal{L}}}^{0}$
as the open sub-scheme of
![]() $B_{{\mathcal{L}}}$
consisting of
$B_{{\mathcal{L}}}$
consisting of
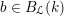 $b\in B_{{\mathcal{L}}}(k)$
such that the image of the map
$b\in B_{{\mathcal{L}}}(k)$
such that the image of the map
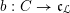 $b:C\rightarrow \mathfrak{c}_{{\mathcal{L}}}$
intersects the discriminant divisor transversally. The following proposition can be extracted from [Reference Donagi and GaitsgoryDG02, Reference Donagi and PantevDP12, Reference NgôNgô06].
$b:C\rightarrow \mathfrak{c}_{{\mathcal{L}}}$
intersects the discriminant divisor transversally. The following proposition can be extracted from [Reference Donagi and GaitsgoryDG02, Reference Donagi and PantevDP12, Reference NgôNgô06].
Proposition 2.6.1.
-
(1) The stack
 $\operatorname{Higgs}_{{\mathcal{L}}}^{\text{reg}}$
is a
$\operatorname{Higgs}_{{\mathcal{L}}}^{\text{reg}}$
is a
 $\mathscr{P}_{{\mathcal{L}}}$
-torsor, which can be trivialized by a choice of a Kostant section
$\mathscr{P}_{{\mathcal{L}}}$
-torsor, which can be trivialized by a choice of a Kostant section
 $\unicode[STIX]{x1D702}_{{\mathcal{L}}^{1/2}}$
.
$\unicode[STIX]{x1D702}_{{\mathcal{L}}^{1/2}}$
. -
(2) One has
 $\operatorname{Higgs}_{{\mathcal{L}}}^{\text{reg}}\times _{B_{{\mathcal{L}}}}B_{{\mathcal{L}}}^{0}=\operatorname{Higgs}_{{\mathcal{L}}}\times _{B_{{\mathcal{L}}}}B_{{\mathcal{L}}}^{0}$
.
$\operatorname{Higgs}_{{\mathcal{L}}}^{\text{reg}}\times _{B_{{\mathcal{L}}}}B_{{\mathcal{L}}}^{0}=\operatorname{Higgs}_{{\mathcal{L}}}\times _{B_{{\mathcal{L}}}}B_{{\mathcal{L}}}^{0}$
. -
(3) The restriction of the universal cameral curve
 $\widetilde{C}_{{\mathcal{L}}}|_{B^{0}}\rightarrow B_{{\mathcal{L}}}^{0}$
to
$\widetilde{C}_{{\mathcal{L}}}|_{B^{0}}\rightarrow B_{{\mathcal{L}}}^{0}$
to
 $B_{{\mathcal{L}}}^{0}$
is smooth. The restriction
$B_{{\mathcal{L}}}^{0}$
is smooth. The restriction
 $\mathscr{P}_{{\mathcal{L}}}|_{B_{{\mathcal{L}}}^{0}}$
to
$\mathscr{P}_{{\mathcal{L}}}|_{B_{{\mathcal{L}}}^{0}}$
to
 $B_{{\mathcal{L}}}^{0}$
is a Beilinson
$B_{{\mathcal{L}}}^{0}$
is a Beilinson
 $1$
-motive.
$1$
-motive.
Remark 2.6.2. Let
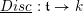 $\text{}\underline{Disc}:\mathfrak{t}\rightarrow k$
be the discriminant function defined by
$\text{}\underline{Disc}:\mathfrak{t}\rightarrow k$
be the discriminant function defined by
 $$\begin{eqnarray}\text{}\underline{Disc}=\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}}d\unicode[STIX]{x1D6FC},\end{eqnarray}$$
$$\begin{eqnarray}\text{}\underline{Disc}=\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}}d\unicode[STIX]{x1D6FC},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6F7}$
is the set of roots of
$\unicode[STIX]{x1D6F7}$
is the set of roots of
![]() $G$
. The function
$G$
. The function
![]() $\text{}\underline{Disc}$
is
$\text{}\underline{Disc}$
is
![]() $\text{W}$
-invariant, and thus descends to a function
$\text{W}$
-invariant, and thus descends to a function
![]() $Disc$
on
$Disc$
on
![]() $\mathfrak{c}$
. Moreover, the function
$\mathfrak{c}$
. Moreover, the function
 $Disc:\mathfrak{c}\rightarrow k$
is
$Disc:\mathfrak{c}\rightarrow k$
is
![]() $\mathbb{G}_{m}$
-equivariant where
$\mathbb{G}_{m}$
-equivariant where
![]() $\mathbb{G}_{m}$
acts on
$\mathbb{G}_{m}$
acts on
![]() $k$
via the character
$k$
via the character
![]() $t\rightarrow t^{N}$
and
$t\rightarrow t^{N}$
and
 $N=|\unicode[STIX]{x1D6F7}|$
. Let
$N=|\unicode[STIX]{x1D6F7}|$
. Let
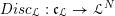 $Disc_{{\mathcal{L}}}:\mathfrak{c}_{{\mathcal{L}}}\rightarrow {\mathcal{L}}^{N}$
be the twist of
$Disc_{{\mathcal{L}}}:\mathfrak{c}_{{\mathcal{L}}}\rightarrow {\mathcal{L}}^{N}$
be the twist of
![]() $Disc$
. For any
$Disc$
. For any
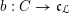 $b:C\rightarrow \mathfrak{c}_{{\mathcal{L}}}$
, we get a section
$b:C\rightarrow \mathfrak{c}_{{\mathcal{L}}}$
, we get a section
 $$\begin{eqnarray}s_{b}\in \unicode[STIX]{x1D6E4}(C,{\mathcal{L}}^{N}).\end{eqnarray}$$
$$\begin{eqnarray}s_{b}\in \unicode[STIX]{x1D6E4}(C,{\mathcal{L}}^{N}).\end{eqnarray}$$
The zeros of
![]() $s_{b}$
is the branch loci
$s_{b}$
is the branch loci
![]() ${\mathcal{B}}$
of the cameral cover
${\mathcal{B}}$
of the cameral cover
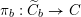 $\unicode[STIX]{x1D70B}_{b}:\widetilde{C}_{b}\rightarrow C$
. If
$\unicode[STIX]{x1D70B}_{b}:\widetilde{C}_{b}\rightarrow C$
. If
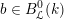 $b\in B_{{\mathcal{L}}}^{0}(k)$
, then
$b\in B_{{\mathcal{L}}}^{0}(k)$
, then
![]() ${\mathcal{B}}$
is multiplicity free. Note that if
${\mathcal{B}}$
is multiplicity free. Note that if
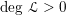 $\text{deg}~{\mathcal{L}}>0$
the branch loci
$\text{deg}~{\mathcal{L}}>0$
the branch loci
![]() ${\mathcal{B}}$
is non-empty.
${\mathcal{B}}$
is non-empty.
2.7 The tautological section
 $\unicode[STIX]{x1D70F}:\mathfrak{c}\rightarrow \operatorname{Lie}\,J$
$\unicode[STIX]{x1D70F}:\mathfrak{c}\rightarrow \operatorname{Lie}\,J$
Recall that by Proposition 2.5.1, there is a canonical isomorphism
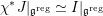 $\unicode[STIX]{x1D712}^{\ast }J|_{\mathfrak{g}^{\text{reg}}}\simeq I|_{\mathfrak{g}^{\text{reg}}}$
. The sheaf of Lie algebras
$\unicode[STIX]{x1D712}^{\ast }J|_{\mathfrak{g}^{\text{reg}}}\simeq I|_{\mathfrak{g}^{\text{reg}}}$
. The sheaf of Lie algebras
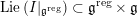 $\operatorname{Lie}\,(I|_{\mathfrak{g}^{\text{reg}}})\subset \mathfrak{g}^{\text{reg}}\times \mathfrak{g}$
admits a tautological section
$\operatorname{Lie}\,(I|_{\mathfrak{g}^{\text{reg}}})\subset \mathfrak{g}^{\text{reg}}\times \mathfrak{g}$
admits a tautological section
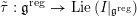 $\tilde{\unicode[STIX]{x1D70F}}:\mathfrak{g}^{\text{reg}}\rightarrow \operatorname{Lie}\,(I|_{\mathfrak{g}^{\text{reg}}})$
given by
$\tilde{\unicode[STIX]{x1D70F}}:\mathfrak{g}^{\text{reg}}\rightarrow \operatorname{Lie}\,(I|_{\mathfrak{g}^{\text{reg}}})$
given by
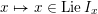 $x\mapsto x\in \operatorname{Lie}\,I_{x}$
for
$x\mapsto x\in \operatorname{Lie}\,I_{x}$
for
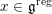 $x\in \mathfrak{g}^{\text{reg}}$
. This section descends to a tautological section
$x\in \mathfrak{g}^{\text{reg}}$
. This section descends to a tautological section
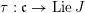 $\unicode[STIX]{x1D70F}:\mathfrak{c}\rightarrow \operatorname{Lie}\,J$
.Footnote
2
Recall the following property of
$\unicode[STIX]{x1D70F}:\mathfrak{c}\rightarrow \operatorname{Lie}\,J$
.Footnote
2
Recall the following property of
![]() $\unicode[STIX]{x1D70F}$
[Reference Chen and ZhuCZ15, Lemma 2.2].
$\unicode[STIX]{x1D70F}$
[Reference Chen and ZhuCZ15, Lemma 2.2].
Lemma 2.7.1. Let
![]() $x\in \mathfrak{g}$
, and
$x\in \mathfrak{g}$
, and
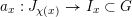 $a_{x}:J_{\unicode[STIX]{x1D712}(x)}\rightarrow I_{x}\subset G$
be the homomorphism as in Proposition 2.5.1(1). Then
$a_{x}:J_{\unicode[STIX]{x1D712}(x)}\rightarrow I_{x}\subset G$
be the homomorphism as in Proposition 2.5.1(1). Then
 $da_{x}(\unicode[STIX]{x1D70F}(x))=x$
, where
$da_{x}(\unicode[STIX]{x1D70F}(x))=x$
, where
![]() $da_{x}$
denotes the differential of
$da_{x}$
denotes the differential of
![]() $a_{x}$
.
$a_{x}$
.
Let us regard
![]() $\operatorname{Lie}\,J$
as a scheme over
$\operatorname{Lie}\,J$
as a scheme over
![]() $\mathfrak{c}$
. Besides the section
$\mathfrak{c}$
. Besides the section
![]() $\unicode[STIX]{x1D70F}$
, there is a canonical map
$\unicode[STIX]{x1D70F}$
, there is a canonical map
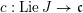 $c:\operatorname{Lie}\,J\rightarrow \mathfrak{c}$
such that
$c:\operatorname{Lie}\,J\rightarrow \mathfrak{c}$
such that
![]() $c\unicode[STIX]{x1D70F}=\operatorname{id}$
. Namely, if we regard
$c\unicode[STIX]{x1D70F}=\operatorname{id}$
. Namely, if we regard
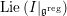 $\operatorname{Lie}\,(I|_{\mathfrak{g}^{\text{reg}}})$
as a scheme, then there is a natural map
$\operatorname{Lie}\,(I|_{\mathfrak{g}^{\text{reg}}})$
as a scheme, then there is a natural map
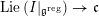 $\operatorname{Lie}\,(I|_{\mathfrak{g}^{\text{reg}}})\rightarrow \mathfrak{c}$
given by
$\operatorname{Lie}\,(I|_{\mathfrak{g}^{\text{reg}}})\rightarrow \mathfrak{c}$
given by
 $$\begin{eqnarray}\operatorname{Lie}\,(I|_{\mathfrak{g}^{\text{reg}}})\subset \mathfrak{g}\times \mathfrak{g}^{\text{reg}}\rightarrow \mathfrak{c}\times \mathfrak{g}^{\text{reg}}\rightarrow \mathfrak{c},\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Lie}\,(I|_{\mathfrak{g}^{\text{reg}}})\subset \mathfrak{g}\times \mathfrak{g}^{\text{reg}}\rightarrow \mathfrak{c}\times \mathfrak{g}^{\text{reg}}\rightarrow \mathfrak{c},\end{eqnarray}$$
which also descends to a morphism
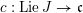 $c:\operatorname{Lie}\,J\rightarrow \mathfrak{c}$
.
$c:\operatorname{Lie}\,J\rightarrow \mathfrak{c}$
.
The morphisms
![]() $\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}$
and
![]() $c$
have global counterparts (see also [Reference Chen and ZhuCZ15, §2.3]). Observe that
$c$
have global counterparts (see also [Reference Chen and ZhuCZ15, §2.3]). Observe that
![]() $\mathbb{G}_{m}$
acts on
$\mathbb{G}_{m}$
acts on
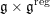 $\mathfrak{g}\times \mathfrak{g}^{\text{reg}}$
via natural homotheties on both factors, and therefore on
$\mathfrak{g}\times \mathfrak{g}^{\text{reg}}$
via natural homotheties on both factors, and therefore on
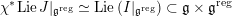 $\unicode[STIX]{x1D712}^{\ast }\operatorname{Lie}\,J|_{\mathfrak{g}^{\text{reg}}}\simeq \operatorname{Lie}\,(I|_{\mathfrak{g}^{\text{reg}}})\subset \mathfrak{g}\times \mathfrak{g}^{\text{reg}}$
. This
$\unicode[STIX]{x1D712}^{\ast }\operatorname{Lie}\,J|_{\mathfrak{g}^{\text{reg}}}\simeq \operatorname{Lie}\,(I|_{\mathfrak{g}^{\text{reg}}})\subset \mathfrak{g}\times \mathfrak{g}^{\text{reg}}$
. This
![]() $\mathbb{G}_{m}$
-action on
$\mathbb{G}_{m}$
-action on
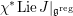 $\unicode[STIX]{x1D712}^{\ast }\operatorname{Lie}\,J|_{\mathfrak{g}^{\text{reg}}}$
descends to a
$\unicode[STIX]{x1D712}^{\ast }\operatorname{Lie}\,J|_{\mathfrak{g}^{\text{reg}}}$
descends to a
![]() $\mathbb{G}_{m}$
-action on
$\mathbb{G}_{m}$
-action on
![]() $\operatorname{Lie}\,J$
, and for any line bundle
$\operatorname{Lie}\,J$
, and for any line bundle
![]() ${\mathcal{L}}$
on
${\mathcal{L}}$
on
![]() $C$
the
$C$
the
![]() ${\mathcal{L}}^{\times }$
-twist
${\mathcal{L}}^{\times }$
-twist
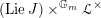 $(\operatorname{Lie}\,J)\times ^{\mathbb{G}_{m}}{\mathcal{L}}^{\times }$
is
$(\operatorname{Lie}\,J)\times ^{\mathbb{G}_{m}}{\mathcal{L}}^{\times }$
is
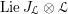 $\operatorname{Lie}\,J_{{\mathcal{L}}}\otimes {\mathcal{L}}$
, where
$\operatorname{Lie}\,J_{{\mathcal{L}}}\otimes {\mathcal{L}}$
, where
![]() $J_{{\mathcal{L}}}$
is introduced in §2.5. In addition, both maps
$J_{{\mathcal{L}}}$
is introduced in §2.5. In addition, both maps
![]() $\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}$
and
![]() $c$
are
$c$
are
![]() $\mathbb{G}_{m}$
-equivariant with respect to this
$\mathbb{G}_{m}$
-equivariant with respect to this
![]() $\mathbb{G}_{m}$
-action on
$\mathbb{G}_{m}$
-action on
![]() $\operatorname{Lie}\,J$
and the natural
$\operatorname{Lie}\,J$
and the natural
![]() $\mathbb{G}_{m}$
-action on
$\mathbb{G}_{m}$
-action on
![]() $\mathfrak{c}$
. Therefore, if we define a vector bundle
$\mathfrak{c}$
. Therefore, if we define a vector bundle
![]() $B_{J,{\mathcal{L}}}$
over
$B_{J,{\mathcal{L}}}$
over
![]() $B_{{\mathcal{L}}}$
, whose fiber over
$B_{{\mathcal{L}}}$
, whose fiber over
![]() $b\in B_{{\mathcal{L}}}$
is
$b\in B_{{\mathcal{L}}}$
is
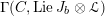 $\unicode[STIX]{x1D6E4}(C,\operatorname{Lie}\,J_{b}\otimes {\mathcal{L}})$
, then by twisting
$\unicode[STIX]{x1D6E4}(C,\operatorname{Lie}\,J_{b}\otimes {\mathcal{L}})$
, then by twisting
![]() $\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}$
and
![]() $c$
by
$c$
by
![]() ${\mathcal{L}}$
, we obtain
${\mathcal{L}}$
, we obtain
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}_{{\mathcal{L}}}:B_{{\mathcal{L}}}\rightarrow B_{J,{\mathcal{L}}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{{\mathcal{L}}}:B_{{\mathcal{L}}}\rightarrow B_{J,{\mathcal{L}}},\end{eqnarray}$$
which is a canonical section of the projection
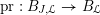 $\operatorname{pr}:B_{J,{\mathcal{L}}}\rightarrow B_{{\mathcal{L}}}$
, and a canonical map
$\operatorname{pr}:B_{J,{\mathcal{L}}}\rightarrow B_{{\mathcal{L}}}$
, and a canonical map
 $$\begin{eqnarray}c_{{\mathcal{L}}}:B_{J,{\mathcal{L}}}\rightarrow B_{{\mathcal{L}}}\end{eqnarray}$$
$$\begin{eqnarray}c_{{\mathcal{L}}}:B_{J,{\mathcal{L}}}\rightarrow B_{{\mathcal{L}}}\end{eqnarray}$$
such that
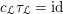 $c_{{\mathcal{L}}}\unicode[STIX]{x1D70F}_{{\mathcal{L}}}=\operatorname{id}$
. As before, we omit the subscript
$c_{{\mathcal{L}}}\unicode[STIX]{x1D70F}_{{\mathcal{L}}}=\operatorname{id}$
. As before, we omit the subscript
![]() $_{{\mathcal{L}}}$
if
$_{{\mathcal{L}}}$
if
![]() ${\mathcal{L}}=\unicode[STIX]{x1D714}$
for brevity.
${\mathcal{L}}=\unicode[STIX]{x1D714}$
for brevity.
Likewise, we introduce the vector bundle
![]() $B_{J,{\mathcal{L}}}^{\ast }$
over
$B_{J,{\mathcal{L}}}^{\ast }$
over
![]() $B_{{\mathcal{L}}}$
whose fiber over
$B_{{\mathcal{L}}}$
whose fiber over
![]() $b$
is
$b$
is
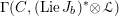 $\unicode[STIX]{x1D6E4}(C,(\operatorname{Lie}\,J_{b})^{\ast }\otimes \,{\mathcal{L}})$
. Observe that
$\unicode[STIX]{x1D6E4}(C,(\operatorname{Lie}\,J_{b})^{\ast }\otimes \,{\mathcal{L}})$
. Observe that
![]() $B_{J,{\mathcal{L}}}^{\ast }$
is not the dual of
$B_{J,{\mathcal{L}}}^{\ast }$
is not the dual of
![]() $B_{J,{\mathcal{L}}}$
. Rather, when
$B_{J,{\mathcal{L}}}$
. Rather, when
![]() ${\mathcal{L}}=\unicode[STIX]{x1D714}$
, it is the pullback
${\mathcal{L}}=\unicode[STIX]{x1D714}$
, it is the pullback
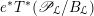 $e^{\ast }T^{\ast }(\mathscr{P}_{{\mathcal{L}}}/B_{{\mathcal{L}}})$
of the cotangent bundle of
$e^{\ast }T^{\ast }(\mathscr{P}_{{\mathcal{L}}}/B_{{\mathcal{L}}})$
of the cotangent bundle of
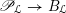 $\mathscr{P}_{{\mathcal{L}}}\rightarrow B_{{\mathcal{L}}}$
along the unit section
$\mathscr{P}_{{\mathcal{L}}}\rightarrow B_{{\mathcal{L}}}$
along the unit section
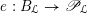 $e:B_{{\mathcal{L}}}\rightarrow \mathscr{P}_{{\mathcal{L}}}$
and will also be denoted by
$e:B_{{\mathcal{L}}}\rightarrow \mathscr{P}_{{\mathcal{L}}}$
and will also be denoted by
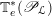 $\mathbb{T}_{e}^{\ast }(\mathscr{P}_{{\mathcal{L}}})$
interchangeably later on. We construct a section
$\mathbb{T}_{e}^{\ast }(\mathscr{P}_{{\mathcal{L}}})$
interchangeably later on. We construct a section
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}_{{\mathcal{L}}}^{\ast }:B_{{\mathcal{L}}}\rightarrow B_{J,{\mathcal{L}}}^{\ast }\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{{\mathcal{L}}}^{\ast }:B_{{\mathcal{L}}}\rightarrow B_{J,{\mathcal{L}}}^{\ast }\end{eqnarray}$$
as follows. The non-degenerate bilinear form
![]() $(\,,\,)$
we fixed in 2.1 induces
$(\,,\,)$
we fixed in 2.1 induces
![]() $\mathfrak{g}\simeq \mathfrak{g}^{\ast }$
, which restricts to a map
$\mathfrak{g}\simeq \mathfrak{g}^{\ast }$
, which restricts to a map
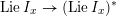 $\operatorname{Lie}\,I_{x}\rightarrow (\operatorname{Lie}\,I_{x})^{\ast }$
for every
$\operatorname{Lie}\,I_{x}\rightarrow (\operatorname{Lie}\,I_{x})^{\ast }$
for every
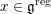 $x\in \mathfrak{g}^{\text{reg}}$
. This map descends to give
$x\in \mathfrak{g}^{\text{reg}}$
. This map descends to give
 $$\begin{eqnarray}\unicode[STIX]{x1D704}:\operatorname{Lie}\,J\rightarrow (\operatorname{Lie}\,J)^{\ast },\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}:\operatorname{Lie}\,J\rightarrow (\operatorname{Lie}\,J)^{\ast },\end{eqnarray}$$
which is
![]() $\mathbb{G}_{m}$
-equivariant. We define
$\mathbb{G}_{m}$
-equivariant. We define
![]() $\unicode[STIX]{x1D70F}_{{\mathcal{L}}}^{\ast }$
as the twist of
$\unicode[STIX]{x1D70F}_{{\mathcal{L}}}^{\ast }$
as the twist of
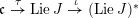 $\mathfrak{c}\stackrel{\unicode[STIX]{x1D70F}}{\rightarrow }\operatorname{Lie}\,J\stackrel{\unicode[STIX]{x1D704}}{\rightarrow }(\operatorname{Lie}\,J)^{\ast }$
. As before, we omit the subscript
$\mathfrak{c}\stackrel{\unicode[STIX]{x1D70F}}{\rightarrow }\operatorname{Lie}\,J\stackrel{\unicode[STIX]{x1D704}}{\rightarrow }(\operatorname{Lie}\,J)^{\ast }$
. As before, we omit the subscript
![]() $_{{\mathcal{L}}}$
if
$_{{\mathcal{L}}}$
if
![]() ${\mathcal{L}}=\unicode[STIX]{x1D714}$
.
${\mathcal{L}}=\unicode[STIX]{x1D714}$
.
We give another interpretation of this map. Observe that the Kostant section
![]() $\unicode[STIX]{x1D705}$
induces the map
$\unicode[STIX]{x1D705}$
induces the map
 $$\begin{eqnarray}v_{\unicode[STIX]{x1D705}}:\mathscr{P}\rightarrow \operatorname{Higgs}_{G}\rightarrow \operatorname{Bun}_{G}\times B\end{eqnarray}$$
$$\begin{eqnarray}v_{\unicode[STIX]{x1D705}}:\mathscr{P}\rightarrow \operatorname{Higgs}_{G}\rightarrow \operatorname{Bun}_{G}\times B\end{eqnarray}$$
over
![]() $B$
, and therefore we have the following.
$B$
, and therefore we have the following.

Lemma 2.7.2. The map
 $$\begin{eqnarray}\mathscr{P}\stackrel{\unicode[STIX]{x1D705}\times \operatorname{id}}{\rightarrow }T^{\ast }(\operatorname{Bun}_{G})\times _{\operatorname{Bun}_{G}}\mathscr{P}\stackrel{(v_{\unicode[STIX]{x1D705}})_{d}}{\rightarrow }T^{\ast }(\mathscr{P}/B)\simeq \mathbb{T}_{e}^{\ast }\mathscr{P}\times _{B}\mathscr{P},\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{P}\stackrel{\unicode[STIX]{x1D705}\times \operatorname{id}}{\rightarrow }T^{\ast }(\operatorname{Bun}_{G})\times _{\operatorname{Bun}_{G}}\mathscr{P}\stackrel{(v_{\unicode[STIX]{x1D705}})_{d}}{\rightarrow }T^{\ast }(\mathscr{P}/B)\simeq \mathbb{T}_{e}^{\ast }\mathscr{P}\times _{B}\mathscr{P},\end{eqnarray}$$
can be identified with
 $$\begin{eqnarray}\mathscr{P}\stackrel{\operatorname{pr}\times \operatorname{id}}{\rightarrow }B\times \mathscr{P}\stackrel{\unicode[STIX]{x1D70F}^{\ast }\times \operatorname{id}}{\longrightarrow }\mathbb{T}_{e}^{\ast }\mathscr{P}\times _{B}\mathscr{P}.\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{P}\stackrel{\operatorname{pr}\times \operatorname{id}}{\rightarrow }B\times \mathscr{P}\stackrel{\unicode[STIX]{x1D70F}^{\ast }\times \operatorname{id}}{\longrightarrow }\mathbb{T}_{e}^{\ast }\mathscr{P}\times _{B}\mathscr{P}.\end{eqnarray}$$
Proof. For
![]() $b\in B$
, we write the restriction of
$b\in B$
, we write the restriction of
![]() $v_{\unicode[STIX]{x1D705}}$
over
$v_{\unicode[STIX]{x1D705}}$
over
![]() $b$
by
$b$
by
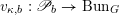 $v_{\unicode[STIX]{x1D705},b}:\mathscr{P}_{b}\rightarrow \operatorname{Bun}_{G}$
. We need to show that for
$v_{\unicode[STIX]{x1D705},b}:\mathscr{P}_{b}\rightarrow \operatorname{Bun}_{G}$
. We need to show that for
![]() $x\in \mathscr{P}_{b}$
, the image of the point
$x\in \mathscr{P}_{b}$
, the image of the point
 $$\begin{eqnarray}\unicode[STIX]{x1D705}(x)\in T_{v_{\unicode[STIX]{x1D705},b}(x)}^{\ast }\operatorname{Bun}_{G}\rightarrow T_{x}^{\ast }\mathscr{P}_{b}\simeq (\mathbb{T}_{e}^{\ast }\mathscr{P})_{b}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D705}(x)\in T_{v_{\unicode[STIX]{x1D705},b}(x)}^{\ast }\operatorname{Bun}_{G}\rightarrow T_{x}^{\ast }\mathscr{P}_{b}\simeq (\mathbb{T}_{e}^{\ast }\mathscr{P})_{b}\end{eqnarray}$$
coincides with
![]() $\unicode[STIX]{x1D70F}^{\ast }(b)$
. Let
$\unicode[STIX]{x1D70F}^{\ast }(b)$
. Let
![]() $E$
denote the
$E$
denote the
![]() $G$
-bundle
$G$
-bundle
![]() $v_{k,b}(x)$
.
$v_{k,b}(x)$
.
Observe that there is a universal
![]() $G$
-torsor
$G$
-torsor
![]() $E_{\text{univ}}$
over
$E_{\text{univ}}$
over
![]() $[\mathfrak{g}/G]$
given by
$[\mathfrak{g}/G]$
given by
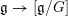 $\mathfrak{g}\rightarrow [\mathfrak{g}/G]$
, and that
$\mathfrak{g}\rightarrow [\mathfrak{g}/G]$
, and that
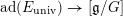 $\operatorname{ad}(E_{\text{univ}})\rightarrow [\mathfrak{g}/G]$
is canonically isomorphic to
$\operatorname{ad}(E_{\text{univ}})\rightarrow [\mathfrak{g}/G]$
is canonically isomorphic to
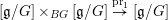 $[\mathfrak{g}/G]\times _{BG}[\mathfrak{g}/G]\stackrel{\operatorname{pr}_{1}}{\rightarrow }[\mathfrak{g}/G]$
. The cotangent map
$[\mathfrak{g}/G]\times _{BG}[\mathfrak{g}/G]\stackrel{\operatorname{pr}_{1}}{\rightarrow }[\mathfrak{g}/G]$
. The cotangent map
 $$\begin{eqnarray}(v_{\unicode[STIX]{x1D705},b})_{d}:T_{v_{\unicode[STIX]{x1D705},b}(x)}^{\ast }\operatorname{Bun}_{G}\rightarrow T_{x}^{\ast }\mathscr{P}_{b}\end{eqnarray}$$
$$\begin{eqnarray}(v_{\unicode[STIX]{x1D705},b})_{d}:T_{v_{\unicode[STIX]{x1D705},b}(x)}^{\ast }\operatorname{Bun}_{G}\rightarrow T_{x}^{\ast }\mathscr{P}_{b}\end{eqnarray}$$
is induced by twisting
 $$\begin{eqnarray}\text{kos}^{\ast }(\operatorname{ad}(E_{\text{univ}}))^{\ast }\rightarrow (\operatorname{Lie}\,J)^{\ast }\end{eqnarray}$$
$$\begin{eqnarray}\text{kos}^{\ast }(\operatorname{ad}(E_{\text{univ}}))^{\ast }\rightarrow (\operatorname{Lie}\,J)^{\ast }\end{eqnarray}$$
by the
 $(G\times \mathbb{G}_{m})$
-torsor
$(G\times \mathbb{G}_{m})$
-torsor
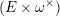 $(E\times \unicode[STIX]{x1D714}^{\times })$
. Therefore, it is enough to show that
$(E\times \unicode[STIX]{x1D714}^{\times })$
. Therefore, it is enough to show that
 $$\begin{eqnarray}\unicode[STIX]{x1D705}(x)\in T_{v_{\unicode[STIX]{x1D705},b}(x)}^{\ast }\operatorname{Bun}_{G}=\unicode[STIX]{x1D6E4}(C,\mathfrak{g}_{E}\otimes \unicode[STIX]{x1D714})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D705}(x)\in T_{v_{\unicode[STIX]{x1D705},b}(x)}^{\ast }\operatorname{Bun}_{G}=\unicode[STIX]{x1D6E4}(C,\mathfrak{g}_{E}\otimes \unicode[STIX]{x1D714})\end{eqnarray}$$
can be identified with the image of
![]() $b$
under
$b$
under
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}(b)\in \unicode[STIX]{x1D6E4}(C,\operatorname{Lie}\,J_{b}\otimes \unicode[STIX]{x1D714})\rightarrow \unicode[STIX]{x1D6E4}(C,\mathfrak{g}_{E}\otimes \unicode[STIX]{x1D714}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}(b)\in \unicode[STIX]{x1D6E4}(C,\operatorname{Lie}\,J_{b}\otimes \unicode[STIX]{x1D714})\rightarrow \unicode[STIX]{x1D6E4}(C,\mathfrak{g}_{E}\otimes \unicode[STIX]{x1D714}).\end{eqnarray}$$
Let us consider the universal situation. Therefore, we need to show that
 $$\begin{eqnarray}\mathfrak{c}\stackrel{\unicode[STIX]{x1D70F}}{\rightarrow }\operatorname{Lie}\,J\rightarrow \text{kos}^{\ast }\operatorname{ad}(E_{\text{univ}})\simeq \mathfrak{c}\times _{BG}[\mathfrak{g}/G]\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{c}\stackrel{\unicode[STIX]{x1D70F}}{\rightarrow }\operatorname{Lie}\,J\rightarrow \text{kos}^{\ast }\operatorname{ad}(E_{\text{univ}})\simeq \mathfrak{c}\times _{BG}[\mathfrak{g}/G]\end{eqnarray}$$
is the same as
 $$\begin{eqnarray}\mathfrak{c}\stackrel{\operatorname{id}\times \text{kos}}{\rightarrow }\mathfrak{c}\times _{BG}[\mathfrak{g}/G].\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{c}\stackrel{\operatorname{id}\times \text{kos}}{\rightarrow }\mathfrak{c}\times _{BG}[\mathfrak{g}/G].\end{eqnarray}$$
However, the composition
 $$\begin{eqnarray}[\mathfrak{g}/G]\stackrel{[\unicode[STIX]{x1D712}]^{\ast }(\unicode[STIX]{x1D70F})}{\rightarrow }[\unicode[STIX]{x1D712}]^{\ast }\operatorname{Lie}\,J\rightarrow \operatorname{ad}(E_{\text{univ}})\simeq [\mathfrak{g}/G]\times _{BG}[\mathfrak{g}/G]\end{eqnarray}$$
$$\begin{eqnarray}[\mathfrak{g}/G]\stackrel{[\unicode[STIX]{x1D712}]^{\ast }(\unicode[STIX]{x1D70F})}{\rightarrow }[\unicode[STIX]{x1D712}]^{\ast }\operatorname{Lie}\,J\rightarrow \operatorname{ad}(E_{\text{univ}})\simeq [\mathfrak{g}/G]\times _{BG}[\mathfrak{g}/G]\end{eqnarray}$$
restricts to a map
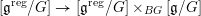 $[\mathfrak{g}^{\text{reg}}/G]\rightarrow [\mathfrak{g}^{\text{reg}}/G]\times _{BG}[\mathfrak{g}/G]$
, which is easily checked to be the diagonal map using the definition of
$[\mathfrak{g}^{\text{reg}}/G]\rightarrow [\mathfrak{g}^{\text{reg}}/G]\times _{BG}[\mathfrak{g}/G]$
, which is easily checked to be the diagonal map using the definition of
![]() $\unicode[STIX]{x1D70F}$
. By pulling back this identification along
$\unicode[STIX]{x1D70F}$
. By pulling back this identification along
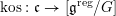 $\text{kos}:\mathfrak{c}\rightarrow [\mathfrak{g}^{\text{reg}}/G]$
, we obtain the claim.◻
$\text{kos}:\mathfrak{c}\rightarrow [\mathfrak{g}^{\text{reg}}/G]$
, we obtain the claim.◻
By the similar argument, we have the following lemma, which will be used in §4. Let
 $\text{j}^{1}:\boldsymbol{\unicode[STIX]{x1D70B}}^{\ast }J\rightarrow T\times \mathfrak{t}$
be the map in Proposition 2.5.1, and let
$\text{j}^{1}:\boldsymbol{\unicode[STIX]{x1D70B}}^{\ast }J\rightarrow T\times \mathfrak{t}$
be the map in Proposition 2.5.1, and let
 $$\begin{eqnarray}d\text{j}^{1}:\boldsymbol{\unicode[STIX]{x1D70B}}^{\ast }\operatorname{Lie}\,J\rightarrow \mathfrak{t}\times \mathfrak{t}\end{eqnarray}$$
$$\begin{eqnarray}d\text{j}^{1}:\boldsymbol{\unicode[STIX]{x1D70B}}^{\ast }\operatorname{Lie}\,J\rightarrow \mathfrak{t}\times \mathfrak{t}\end{eqnarray}$$
denote its differential. Consider the pullback
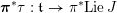 $\boldsymbol{\unicode[STIX]{x1D70B}}^{\ast }\unicode[STIX]{x1D70F}:\mathfrak{t}\rightarrow \unicode[STIX]{x1D70B}^{\ast }\operatorname{Lie}\,J$
of
$\boldsymbol{\unicode[STIX]{x1D70B}}^{\ast }\unicode[STIX]{x1D70F}:\mathfrak{t}\rightarrow \unicode[STIX]{x1D70B}^{\ast }\operatorname{Lie}\,J$
of
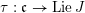 $\unicode[STIX]{x1D70F}:\mathfrak{c}\rightarrow \operatorname{Lie}\,J$
along
$\unicode[STIX]{x1D70F}:\mathfrak{c}\rightarrow \operatorname{Lie}\,J$
along
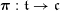 $\boldsymbol{\unicode[STIX]{x1D70B}}:\mathfrak{t}\rightarrow \mathfrak{c}$
.
$\boldsymbol{\unicode[STIX]{x1D70B}}:\mathfrak{t}\rightarrow \mathfrak{c}$
.
Lemma 2.7.3. The composition
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}:\mathfrak{t}\stackrel{\boldsymbol{\unicode[STIX]{x1D70B}}^{\ast }\unicode[STIX]{x1D70F}}{\rightarrow }\boldsymbol{\unicode[STIX]{x1D70B}}^{\ast }\operatorname{Lie}\,J_{}\stackrel{d\text{j}^{1}}{\rightarrow }\mathfrak{t}\times \mathfrak{t}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}:\mathfrak{t}\stackrel{\boldsymbol{\unicode[STIX]{x1D70B}}^{\ast }\unicode[STIX]{x1D70F}}{\rightarrow }\boldsymbol{\unicode[STIX]{x1D70B}}^{\ast }\operatorname{Lie}\,J_{}\stackrel{d\text{j}^{1}}{\rightarrow }\mathfrak{t}\times \mathfrak{t}\end{eqnarray}$$
is equal to the diagonal map
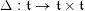 $\unicode[STIX]{x1D6E5}:\mathfrak{t}\rightarrow \mathfrak{t}\times \mathfrak{t}$
.
$\unicode[STIX]{x1D6E5}:\mathfrak{t}\rightarrow \mathfrak{t}\times \mathfrak{t}$
.
Proof. For an embedding
![]() $\mathfrak{t}\subset \mathfrak{g}$
, the restriction of
$\mathfrak{t}\subset \mathfrak{g}$
, the restriction of
![]() $d\text{j}^{1}$
to
$d\text{j}^{1}$
to
 $\mathfrak{t}^{\text{reg}}=\mathfrak{t}\cap \mathfrak{g}^{\text{reg}}$
is just the restriction to
$\mathfrak{t}^{\text{reg}}=\mathfrak{t}\cap \mathfrak{g}^{\text{reg}}$
is just the restriction to
![]() $\mathfrak{t}^{\text{reg}}$
of the isomorphism
$\mathfrak{t}^{\text{reg}}$
of the isomorphism
 $\operatorname{Lie}\,J|_{\mathfrak{g}^{\text{reg}}}\simeq \operatorname{Lie}\,(I|_{\mathfrak{g}^{\text{reg}}})$
. This follows from the construction of
$\operatorname{Lie}\,J|_{\mathfrak{g}^{\text{reg}}}\simeq \operatorname{Lie}\,(I|_{\mathfrak{g}^{\text{reg}}})$
. This follows from the construction of
![]() $\text{j}^{1}$
as in [Reference NgôNgô10, Proposition 2.4.2]. Therefore, the restriction of
$\text{j}^{1}$
as in [Reference NgôNgô10, Proposition 2.4.2]. Therefore, the restriction of
![]() $\unicode[STIX]{x1D6FF}$
to
$\unicode[STIX]{x1D6FF}$
to
![]() $\mathfrak{t}^{\text{reg}}$
is just the diagonal map. The lemma then follows.◻
$\mathfrak{t}^{\text{reg}}$
is just the diagonal map. The lemma then follows.◻
3 Classical duality
In this section, we fix a smooth projective curve
![]() $C$
over
$C$
over
![]() $k$
and a line bundle
$k$
and a line bundle
![]() ${\mathcal{L}}$
on
${\mathcal{L}}$
on
![]() $C$
such that
$C$
such that
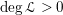 $\deg {\mathcal{L}}>0$
. Except §3.7, we also fix a connected reductive group
$\deg {\mathcal{L}}>0$
. Except §3.7, we also fix a connected reductive group
![]() $G$
over
$G$
over
![]() $k$
. We assume that
$k$
. We assume that
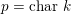 $p=\operatorname{char}~k$
does not divide the order of the Weyl group of
$p=\operatorname{char}~k$
does not divide the order of the Weyl group of
![]() $G$
. We show that the
$G$
. We show that the
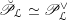 $\breve{\mathscr{P}}_{{\mathcal{L}}}\simeq \mathscr{P}_{{\mathcal{L}}}^{\vee }$
as Picard stacks over
$\breve{\mathscr{P}}_{{\mathcal{L}}}\simeq \mathscr{P}_{{\mathcal{L}}}^{\vee }$
as Picard stacks over
![]() $B^{0}$
. Note that this duality for
$B^{0}$
. Note that this duality for
![]() $k=\mathbb{C}$
is the main theorem of [Reference Donagi and PantevDP12] (for
$k=\mathbb{C}$
is the main theorem of [Reference Donagi and PantevDP12] (for
 $G=\operatorname{SL}_{n}$
, see [Reference Hausel and ThaddeusHT03]). However, as mentioned by the authors, transcendental arguments are used in [Reference Donagi and PantevDP12] in an essential way, and therefore cannot be applied directly to our situation. Our argument works for any algebraically closed field
$G=\operatorname{SL}_{n}$
, see [Reference Hausel and ThaddeusHT03]). However, as mentioned by the authors, transcendental arguments are used in [Reference Donagi and PantevDP12] in an essential way, and therefore cannot be applied directly to our situation. Our argument works for any algebraically closed field
![]() $k$
of characteristic zero or
$k$
of characteristic zero or
![]() $p$
with
$p$
with
![]() $p\nmid |\text{W}|$
.
$p\nmid |\text{W}|$
.
In fact, it is not hard to construct a canonical isogeny
![]() $\mathfrak{D}_{\text{cl}}$
between
$\mathfrak{D}_{\text{cl}}$
between
![]() $\breve{\mathscr{P}}_{{\mathcal{L}}}$
and
$\breve{\mathscr{P}}_{{\mathcal{L}}}$
and
![]() $\mathscr{P}_{{\mathcal{L}}}^{\vee }$
. If the adjoint group of
$\mathscr{P}_{{\mathcal{L}}}^{\vee }$
. If the adjoint group of
![]() $G$
does not contain a simple factor of type
$G$
does not contain a simple factor of type
![]() $\text{B}$
or
$\text{B}$
or
![]() $\text{C}$
, then to show that
$\text{C}$
, then to show that
![]() $\mathfrak{D}_{\text{cl}}$
is an isomorphism is relatively easy. It is to show that
$\mathfrak{D}_{\text{cl}}$
is an isomorphism is relatively easy. It is to show that
![]() $\mathfrak{D}_{\text{cl}}$
is an isomorphism in the remaining cases that some complicated calculations are needed.
$\mathfrak{D}_{\text{cl}}$
is an isomorphism in the remaining cases that some complicated calculations are needed.
Observe in this section, we do not need to assume that
![]() ${\mathcal{L}}=\unicode[STIX]{x1D714}_{C}$
. We only need the assumption that
${\mathcal{L}}=\unicode[STIX]{x1D714}_{C}$
. We only need the assumption that
![]() $\text{deg}~{\mathcal{L}}$
is positive. However, to simplify the notations, we still omit the subscript
$\text{deg}~{\mathcal{L}}$
is positive. However, to simplify the notations, we still omit the subscript
![]() $_{{\mathcal{L}}}$
.
$_{{\mathcal{L}}}$
.
3.1 Galois description of
 $\mathscr{P}$
$\mathscr{P}$
We first introduce several auxiliary Picard stacks.
Let
![]() $\widetilde{C}\rightarrow B$
be the universal cameral curve. There is a natural action of
$\widetilde{C}\rightarrow B$
be the universal cameral curve. There is a natural action of
![]() $\text{W}$
on
$\text{W}$
on
![]() $\widetilde{C}$
. For a
$\widetilde{C}$
. For a
![]() $T$
-torsor
$T$
-torsor
![]() $E_{T}$
on
$E_{T}$
on
![]() $\widetilde{C}$
, and an element
$\widetilde{C}$
, and an element
![]() $w\in \text{W}$
, there are two ways to produce a new
$w\in \text{W}$
, there are two ways to produce a new
![]() $T$
-torsor. Namely, the first is via the pullback
$T$
-torsor. Namely, the first is via the pullback
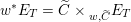 $w^{\ast }E_{T}=\widetilde{C}\times _{w,\widetilde{C}}E_{T}$
, and the second is via the induction
$w^{\ast }E_{T}=\widetilde{C}\times _{w,\widetilde{C}}E_{T}$
, and the second is via the induction
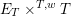 $E_{T}\times ^{T,w}T$
. We denote
$E_{T}\times ^{T,w}T$
. We denote
 $$\begin{eqnarray}w(E_{T})=((w^{-1})^{\ast }E_{T})\times ^{T,w}T.\end{eqnarray}$$
$$\begin{eqnarray}w(E_{T})=((w^{-1})^{\ast }E_{T})\times ^{T,w}T.\end{eqnarray}$$
Clearly, the assignment
 $E_{T}\mapsto w(E_{T})$
defines an action of
$E_{T}\mapsto w(E_{T})$
defines an action of
![]() $W$
on
$W$
on
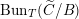 $\operatorname{Bun}_{T}(\widetilde{C}/B)$
, i.e., for every
$\operatorname{Bun}_{T}(\widetilde{C}/B)$
, i.e., for every
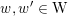 $w,w^{\prime }\in \text{W}$
, there is a canonical isomorphism
$w,w^{\prime }\in \text{W}$
, there is a canonical isomorphism
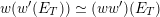 $w(w^{\prime }(E_{T}))\simeq (ww^{\prime })(E_{T})$
satisfying the usual cocycle conditions.
$w(w^{\prime }(E_{T}))\simeq (ww^{\prime })(E_{T})$
satisfying the usual cocycle conditions.
Example 3.1.1. Let us describe
![]() $w(E_{T})$
more explicitly in the case
$w(E_{T})$
more explicitly in the case
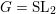 $G=\operatorname{SL}_{2}$
. Let
$G=\operatorname{SL}_{2}$
. Let
![]() $s$
be the unique non-trivial element in the Weyl group, acting on the cameral curve
$s$
be the unique non-trivial element in the Weyl group, acting on the cameral curve
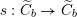 $s:\widetilde{C}_{b}\rightarrow \widetilde{C}_{b}$
. If we identify
$s:\widetilde{C}_{b}\rightarrow \widetilde{C}_{b}$
. If we identify
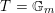 $T=\mathbb{G}_{m}$
-torsors with invertible sheaves
$T=\mathbb{G}_{m}$
-torsors with invertible sheaves
![]() ${\mathcal{L}}$
, then
${\mathcal{L}}$
, then
 $$\begin{eqnarray}s({\mathcal{L}})=s^{\ast }{\mathcal{L}}^{-1}.\end{eqnarray}$$
$$\begin{eqnarray}s({\mathcal{L}})=s^{\ast }{\mathcal{L}}^{-1}.\end{eqnarray}$$
Let
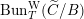 $\operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B)$
(or
$\operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B)$
(or
![]() $\operatorname{Bun}_{T}^{\text{W}}$
for simplicity) denote the Picard stack of strongly
$\operatorname{Bun}_{T}^{\text{W}}$
for simplicity) denote the Picard stack of strongly
![]() $\text{W}$
-equivariant
$\text{W}$
-equivariant
![]() $T$
-torsors on
$T$
-torsors on
![]() $\widetilde{C}/B$
. By definition, for a
$\widetilde{C}/B$
. By definition, for a
![]() $B$
-scheme
$B$
-scheme
![]() $S$
,
$S$
,
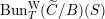 $\operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B)(S)$
is the groupoid of
$\operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B)(S)$
is the groupoid of
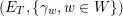 $(E_{T},\{\unicode[STIX]{x1D6FE}_{w},w\in W\})$
, where
$(E_{T},\{\unicode[STIX]{x1D6FE}_{w},w\in W\})$
, where
![]() $E_{T}$
is a
$E_{T}$
is a
![]() $T$
-torsor on
$T$
-torsor on
![]() $\widetilde{C}_{S}$
, and
$\widetilde{C}_{S}$
, and
 $\unicode[STIX]{x1D6FE}_{w}:w(E_{T})\simeq E_{T}$
is an isomorphism, satisfying the natural compatibility conditions. Another way to formulate these compatibility conditions is provided in [Reference Donagi and GaitsgoryDG02]. Namely, for a
$\unicode[STIX]{x1D6FE}_{w}:w(E_{T})\simeq E_{T}$
is an isomorphism, satisfying the natural compatibility conditions. Another way to formulate these compatibility conditions is provided in [Reference Donagi and GaitsgoryDG02]. Namely, for a
![]() $T$
-torsor
$T$
-torsor
![]() $E_{T}$
, let
$E_{T}$
, let
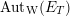 $\operatorname{Aut}_{\text{W}}(E_{T})$
be the group consisting of
$\operatorname{Aut}_{\text{W}}(E_{T})$
be the group consisting of
![]() $(w,\unicode[STIX]{x1D6FE}_{w})$
, where
$(w,\unicode[STIX]{x1D6FE}_{w})$
, where
![]() $w\in \text{W}$
and
$w\in \text{W}$
and
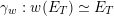 $\unicode[STIX]{x1D6FE}_{w}:w(E_{T})\simeq E_{T}$
is an isomorphism. Then there is a natural projection
$\unicode[STIX]{x1D6FE}_{w}:w(E_{T})\simeq E_{T}$
is an isomorphism. Then there is a natural projection
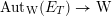 $\operatorname{Aut}_{\text{W}}(E_{T})\rightarrow \text{W}$
. Then an object of
$\operatorname{Aut}_{\text{W}}(E_{T})\rightarrow \text{W}$
. Then an object of
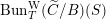 $\operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B)(S)$
is a pair
$\operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B)(S)$
is a pair
![]() $(E_{T},\unicode[STIX]{x1D6FE})$
, where
$(E_{T},\unicode[STIX]{x1D6FE})$
, where
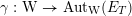 $\unicode[STIX]{x1D6FE}:\text{W}\rightarrow \operatorname{Aut}_{\text{W}}(E_{T})$
is a splitting of the projection.
$\unicode[STIX]{x1D6FE}:\text{W}\rightarrow \operatorname{Aut}_{\text{W}}(E_{T})$
is a splitting of the projection.
For later purpose, it is worthwhile to give another description of
![]() $\operatorname{Bun}_{T}^{\text{W}}$
. Namely, there is a non-constant group scheme
$\operatorname{Bun}_{T}^{\text{W}}$
. Namely, there is a non-constant group scheme
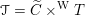 ${\mathcal{T}}=\widetilde{C}\times ^{\text{W}}T$
on the stack
${\mathcal{T}}=\widetilde{C}\times ^{\text{W}}T$
on the stack
![]() $[\widetilde{C}/\text{W}]$
. Then the pullback functor induces an isomorphism from the stack
$[\widetilde{C}/\text{W}]$
. Then the pullback functor induces an isomorphism from the stack
![]() $\operatorname{Bun}_{{\mathcal{T}}}$
of
$\operatorname{Bun}_{{\mathcal{T}}}$
of
![]() ${\mathcal{T}}$
-torsors on
${\mathcal{T}}$
-torsors on
![]() $[\widetilde{C}/W]$
to
$[\widetilde{C}/W]$
to
![]() $\operatorname{Bun}_{T}^{\text{W}}$
.
$\operatorname{Bun}_{T}^{\text{W}}$
.
In [Reference Donagi and GaitsgoryDG02], a Galois description of
![]() $\mathscr{P}$
in terms of
$\mathscr{P}$
in terms of
![]() $\operatorname{Bun}_{T}^{\text{W}}$
is given. We here refine their description.
$\operatorname{Bun}_{T}^{\text{W}}$
is given. We here refine their description.
Let
![]() $\mathscr{P}^{1}$
be the Picard stack over
$\mathscr{P}^{1}$
be the Picard stack over
![]() $B$
classifying
$B$
classifying
![]() $J^{1}$
-torsors on
$J^{1}$
-torsors on
![]() $C\times B$
. First, we claim that there is a canonical morphism
$C\times B$
. First, we claim that there is a canonical morphism
 $$\begin{eqnarray}j^{1,\mathscr{P}}:\mathscr{P}^{1}\rightarrow \operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B).\end{eqnarray}$$
$$\begin{eqnarray}j^{1,\mathscr{P}}:\mathscr{P}^{1}\rightarrow \operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B).\end{eqnarray}$$
To construct
![]() $j^{1,\mathscr{P}}$
, recall that
$j^{1,\mathscr{P}}$
, recall that
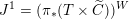 $J^{1}=(\unicode[STIX]{x1D70B}_{\ast }(T\times \widetilde{C}))^{W}$
, where
$J^{1}=(\unicode[STIX]{x1D70B}_{\ast }(T\times \widetilde{C}))^{W}$
, where
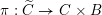 $\unicode[STIX]{x1D70B}:\widetilde{C}\rightarrow C\times B$
is the projection, and therefore, for any
$\unicode[STIX]{x1D70B}:\widetilde{C}\rightarrow C\times B$
is the projection, and therefore, for any
![]() $J^{1}$
-torsor
$J^{1}$
-torsor
![]() $E_{J^{1}}$
on
$E_{J^{1}}$
on
![]() $C\times S$
(where
$C\times S$
(where
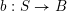 $b:S\rightarrow B$
is a test scheme), one can form a
$b:S\rightarrow B$
is a test scheme), one can form a
![]() $T$
-torsor on
$T$
-torsor on
![]() $\widetilde{C}_{S}$
by
$\widetilde{C}_{S}$
by
 $$\begin{eqnarray}E_{T}:=\unicode[STIX]{x1D70B}^{\ast }E_{J^{1}}\times ^{\unicode[STIX]{x1D70B}^{\ast }J^{1}}T.\end{eqnarray}$$
$$\begin{eqnarray}E_{T}:=\unicode[STIX]{x1D70B}^{\ast }E_{J^{1}}\times ^{\unicode[STIX]{x1D70B}^{\ast }J^{1}}T.\end{eqnarray}$$
Clearly,
![]() $E_{T}$
carries on a strongly
$E_{T}$
carries on a strongly
![]() $\text{W}$
-equivariant structure
$\text{W}$
-equivariant structure
![]() $\unicode[STIX]{x1D6FE}$
, and
$\unicode[STIX]{x1D6FE}$
, and
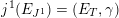 $j^{1}(E_{J^{1}})=(E_{T},\unicode[STIX]{x1D6FE})$
defines the morphism
$j^{1}(E_{J^{1}})=(E_{T},\unicode[STIX]{x1D6FE})$
defines the morphism
![]() $j^{1,\mathscr{P}}$
.
$j^{1,\mathscr{P}}$
.
The morphism
![]() $j^{1,\mathscr{P}}$
, in general, is not an isomorphism. Let us describe the image. Let
$j^{1,\mathscr{P}}$
, in general, is not an isomorphism. Let us describe the image. Let
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}$
be a root and let
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}$
be a root and let
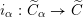 $i_{\unicode[STIX]{x1D6FC}}:\widetilde{C}_{\unicode[STIX]{x1D6FC}}\rightarrow \widetilde{C}$
be the inclusion of the fixed point subscheme of the reflection
$i_{\unicode[STIX]{x1D6FC}}:\widetilde{C}_{\unicode[STIX]{x1D6FC}}\rightarrow \widetilde{C}$
be the inclusion of the fixed point subscheme of the reflection
![]() $s_{\unicode[STIX]{x1D6FC}}$
. Let
$s_{\unicode[STIX]{x1D6FC}}$
. Let
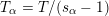 $T_{\unicode[STIX]{x1D6FC}}=T/(s_{\unicode[STIX]{x1D6FC}}-1)$
be the torus of coinvariants of the reflection
$T_{\unicode[STIX]{x1D6FC}}=T/(s_{\unicode[STIX]{x1D6FC}}-1)$
be the torus of coinvariants of the reflection
![]() $s_{\unicode[STIX]{x1D6FC}}$
. Then
$s_{\unicode[STIX]{x1D6FC}}$
. Then
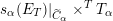 $s_{\unicode[STIX]{x1D6FC}}(E_{T})|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}}\times ^{T}T_{\unicode[STIX]{x1D6FC}}$
is canonically isomorphic to
$s_{\unicode[STIX]{x1D6FC}}(E_{T})|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}}\times ^{T}T_{\unicode[STIX]{x1D6FC}}$
is canonically isomorphic to
 $E_{T}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}}\times ^{T}T_{\unicode[STIX]{x1D6FC}}$
and therefore
$E_{T}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}}\times ^{T}T_{\unicode[STIX]{x1D6FC}}$
and therefore
![]() $\unicode[STIX]{x1D6FE}_{s_{\unicode[STIX]{x1D6FC}}}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}}$
induces an automorphism of the
$\unicode[STIX]{x1D6FE}_{s_{\unicode[STIX]{x1D6FC}}}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}}$
induces an automorphism of the
![]() $T_{\unicode[STIX]{x1D6FC}}$
-torsor
$T_{\unicode[STIX]{x1D6FC}}$
-torsor
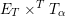 $E_{T}\times ^{T}T_{\unicode[STIX]{x1D6FC}}$
. In other words, there is a natural map
$E_{T}\times ^{T}T_{\unicode[STIX]{x1D6FC}}$
. In other words, there is a natural map
 $$\begin{eqnarray}r=\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}}r_{\unicode[STIX]{x1D6FC}}:\operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B)\rightarrow \biggl(\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}}\operatorname{Res}_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}/B}(T_{\unicode[STIX]{x1D6FC}}\times \widetilde{C}_{\unicode[STIX]{x1D6FC}})\biggr)^{\text{W}}.\end{eqnarray}$$
$$\begin{eqnarray}r=\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}}r_{\unicode[STIX]{x1D6FC}}:\operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B)\rightarrow \biggl(\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}}\operatorname{Res}_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}/B}(T_{\unicode[STIX]{x1D6FC}}\times \widetilde{C}_{\unicode[STIX]{x1D6FC}})\biggr)^{\text{W}}.\end{eqnarray}$$
It is easy to see that
 $r\circ j^{1,\mathscr{P}}$
is trivial, and one can show the following.
$r\circ j^{1,\mathscr{P}}$
is trivial, and one can show the following.
Lemma 3.1.2. We have
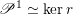 $\mathscr{P}^{1}\simeq \ker r$
. In other words,
$\mathscr{P}^{1}\simeq \ker r$
. In other words,
![]() $\mathscr{P}^{1}(S)$
consists of those strongly
$\mathscr{P}^{1}(S)$
consists of those strongly
![]() $\text{W}$
-equivariant
$\text{W}$
-equivariant
![]() $T$
-torsors
$T$
-torsors
![]() $(E_{T},\unicode[STIX]{x1D6FE})$
such that the induced automorphism of
$(E_{T},\unicode[STIX]{x1D6FE})$
such that the induced automorphism of
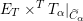 $E_{T}\times ^{T}T_{\unicode[STIX]{x1D6FC}}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}}$
is trivial for every
$E_{T}\times ^{T}T_{\unicode[STIX]{x1D6FC}}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}}$
is trivial for every
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}$
.
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}$
.
Proof. We shall show that every strongly
![]() $\text{W}$
-equivariant
$\text{W}$
-equivariant
![]() $T$
-torsor
$T$
-torsor
![]() $(E_{T},\unicode[STIX]{x1D6FE})$
such that
$(E_{T},\unicode[STIX]{x1D6FE})$
such that
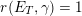 $r(E_{T},\unicode[STIX]{x1D6FE})=1$
is Zariski locally on
$r(E_{T},\unicode[STIX]{x1D6FE})=1$
is Zariski locally on
![]() $\widetilde{C}$
isomorphic to the trivial one, i.e., the trivial
$\widetilde{C}$
isomorphic to the trivial one, i.e., the trivial
![]() $T$
-torsor together with the canonical
$T$
-torsor together with the canonical
![]() $\text{W}$
-equivariance structure. If this is the case, then the inverse map from
$\text{W}$
-equivariance structure. If this is the case, then the inverse map from
 $\ker r\rightarrow \mathscr{P}^{1}$
is given as follows. For every strongly
$\ker r\rightarrow \mathscr{P}^{1}$
is given as follows. For every strongly
![]() $\text{W}$
-equivariant
$\text{W}$
-equivariant
![]() $T$
-torsor
$T$
-torsor
![]() $(E_{T},\unicode[STIX]{x1D6FE})$
,
$(E_{T},\unicode[STIX]{x1D6FE})$
,
![]() $\unicode[STIX]{x1D70B}_{\ast }E_{T}$
carries on an action of
$\unicode[STIX]{x1D70B}_{\ast }E_{T}$
carries on an action of
![]() $\text{W}$
. Namely, let
$\text{W}$
. Namely, let
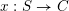 $x:S\rightarrow C$
be a point and
$x:S\rightarrow C$
be a point and
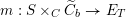 $m:S\times _{C}\widetilde{C}_{b}\rightarrow E_{T}$
be a point of
$m:S\times _{C}\widetilde{C}_{b}\rightarrow E_{T}$
be a point of
![]() $\unicode[STIX]{x1D70B}_{\ast }E_{T}$
over
$\unicode[STIX]{x1D70B}_{\ast }E_{T}$
over
![]() $x$
. Then
$x$
. Then
![]() $w(m)$
is the point of
$w(m)$
is the point of
![]() $\unicode[STIX]{x1D70B}_{\ast }E_{T}$
over
$\unicode[STIX]{x1D70B}_{\ast }E_{T}$
over
![]() $x$
given by
$x$
given by
 $$\begin{eqnarray}S\times _{C}\widetilde{C}_{b}\stackrel{1\times w^{-1}}{\rightarrow }S\times _{C}\widetilde{C}_{b}\stackrel{w^{-1}(m)}{\rightarrow }(w^{-1})^{\ast }E_{T}\rightarrow w(E_{T})\stackrel{s(w)}{\rightarrow }E_{T}.\end{eqnarray}$$
$$\begin{eqnarray}S\times _{C}\widetilde{C}_{b}\stackrel{1\times w^{-1}}{\rightarrow }S\times _{C}\widetilde{C}_{b}\stackrel{w^{-1}(m)}{\rightarrow }(w^{-1})^{\ast }E_{T}\rightarrow w(E_{T})\stackrel{s(w)}{\rightarrow }E_{T}.\end{eqnarray}$$
This
![]() $\text{W}$
-action on
$\text{W}$
-action on
![]() $\unicode[STIX]{x1D70B}_{\ast }E_{T}$
is compatible with the action of
$\unicode[STIX]{x1D70B}_{\ast }E_{T}$
is compatible with the action of
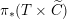 $\unicode[STIX]{x1D70B}_{\ast }(T\times \widetilde{C})$
in the sense that
$\unicode[STIX]{x1D70B}_{\ast }(T\times \widetilde{C})$
in the sense that
 $w(mt)=w(m)w(t)$
. Now let
$w(mt)=w(m)w(t)$
. Now let
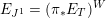 $E_{J^{1}}=(\unicode[STIX]{x1D70B}_{\ast }E_{T})^{W}$
, then as
$E_{J^{1}}=(\unicode[STIX]{x1D70B}_{\ast }E_{T})^{W}$
, then as
![]() $(E,\unicode[STIX]{x1D6FE})$
is locally isomorphic to the trivial one,
$(E,\unicode[STIX]{x1D6FE})$
is locally isomorphic to the trivial one,
![]() $E_{J^{1}}$
is locally isomorphic to
$E_{J^{1}}$
is locally isomorphic to
![]() $J^{1}$
, and therefore is a
$J^{1}$
, and therefore is a
![]() $J^{1}$
-torsor on
$J^{1}$
-torsor on
![]() $C$
.
$C$
.
To prove the local triviality, we follow the argument as in [Reference Donagi and GaitsgoryDG02, Proposition 16.4]. One reduces to prove the statement for a neighborhood around a point
 $x\in \cap _{\unicode[STIX]{x1D6FC}}\widetilde{C}_{\unicode[STIX]{x1D6FC}}$
. By replacing
$x\in \cap _{\unicode[STIX]{x1D6FC}}\widetilde{C}_{\unicode[STIX]{x1D6FC}}$
. By replacing
![]() $\widetilde{C}$
by the local ring around
$\widetilde{C}$
by the local ring around
![]() $x$
, one can assume that
$x$
, one can assume that
![]() $E_{T}$
is trivial. Pick up a trivialization, then the
$E_{T}$
is trivial. Pick up a trivialization, then the
![]() $\text{W}$
-equivariance structure on
$\text{W}$
-equivariance structure on
![]() $E_{T}$
amounts to a 1-cocycle
$E_{T}$
amounts to a 1-cocycle
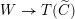 $W\rightarrow T(\widetilde{C})$
. By evaluating
$W\rightarrow T(\widetilde{C})$
. By evaluating
![]() $T(\widetilde{C})$
at the unique closed point
$T(\widetilde{C})$
at the unique closed point
![]() $x$
, there is a short exact sequence
$x$
, there is a short exact sequence
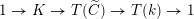 $1\rightarrow K\rightarrow T(\widetilde{C})\rightarrow T(k)\rightarrow 1$
. The condition
$1\rightarrow K\rightarrow T(\widetilde{C})\rightarrow T(k)\rightarrow 1$
. The condition
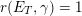 $r(E_{T},\unicode[STIX]{x1D6FE})=1$
would mean that the cocycle takes value in
$r(E_{T},\unicode[STIX]{x1D6FE})=1$
would mean that the cocycle takes value in
![]() $K$
. Since there exists a filtration on
$K$
. Since there exists a filtration on
![]() $K$
, such that the associated graded is an
$K$
, such that the associated graded is an
![]() $\mathbb{F}_{p}$
-vector space and
$\mathbb{F}_{p}$
-vector space and
![]() $p\nmid |\text{W}|$
, this cocycle is trivial.◻
$p\nmid |\text{W}|$
, this cocycle is trivial.◻
Recall that in [Reference Donagi and GaitsgoryDG02, Reference NgôNgô06], an open embedding
![]() $J\rightarrow J^{1}$
is constructed. To describe the cokernel, we need some notations. Let
$J\rightarrow J^{1}$
is constructed. To describe the cokernel, we need some notations. Let
![]() $\breve{\unicode[STIX]{x1D6FC}}\in \breve{\unicode[STIX]{x1D6F7}}$
be a coroot. Let
$\breve{\unicode[STIX]{x1D6FC}}\in \breve{\unicode[STIX]{x1D6F7}}$
be a coroot. Let
 $$\begin{eqnarray}\unicode[STIX]{x1D707}_{\breve{\unicode[STIX]{x1D6FC}}}:=\ker (\breve{\unicode[STIX]{x1D6FC}}:\mathbb{G}_{m}\rightarrow T).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{\breve{\unicode[STIX]{x1D6FC}}}:=\ker (\breve{\unicode[STIX]{x1D6FC}}:\mathbb{G}_{m}\rightarrow T).\end{eqnarray}$$
This is either trivial, or
![]() $\unicode[STIX]{x1D707}_{2}$
, depending on whether
$\unicode[STIX]{x1D707}_{2}$
, depending on whether
![]() $\breve{\unicode[STIX]{x1D6FC}}$
is primitive or not. Let
$\breve{\unicode[STIX]{x1D6FC}}$
is primitive or not. Let
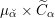 $\unicode[STIX]{x1D707}_{\breve{\unicode[STIX]{x1D6FC}}}\times \widetilde{C}_{\unicode[STIX]{x1D6FC}}$
be the constant group scheme over
$\unicode[STIX]{x1D707}_{\breve{\unicode[STIX]{x1D6FC}}}\times \widetilde{C}_{\unicode[STIX]{x1D6FC}}$
be the constant group scheme over
![]() $\widetilde{C}_{\unicode[STIX]{x1D6FC}}$
, regarded as a sheaf of groups over
$\widetilde{C}_{\unicode[STIX]{x1D6FC}}$
, regarded as a sheaf of groups over
![]() $\widetilde{C}_{\unicode[STIX]{x1D6FC}}$
, and let
$\widetilde{C}_{\unicode[STIX]{x1D6FC}}$
, and let
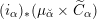 $(i_{\unicode[STIX]{x1D6FC}})_{\ast }(\unicode[STIX]{x1D707}_{\breve{\unicode[STIX]{x1D6FC}}}\times \widetilde{C}_{\unicode[STIX]{x1D6FC}})$
be its push forward to
$(i_{\unicode[STIX]{x1D6FC}})_{\ast }(\unicode[STIX]{x1D707}_{\breve{\unicode[STIX]{x1D6FC}}}\times \widetilde{C}_{\unicode[STIX]{x1D6FC}})$
be its push forward to
![]() $\widetilde{C}$
. Now, the result of [Reference Donagi and GaitsgoryDG02, §§11 and 12] can be reformulated as follows: there is a natural exact sequence of sheaves of groups on
$\widetilde{C}$
. Now, the result of [Reference Donagi and GaitsgoryDG02, §§11 and 12] can be reformulated as follows: there is a natural exact sequence of sheaves of groups on
![]() $C$
.
$C$
.
 $$\begin{eqnarray}1\rightarrow J\rightarrow J^{1}\rightarrow \unicode[STIX]{x1D70B}_{\ast }\biggl(\bigoplus _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}}(i_{\unicode[STIX]{x1D6FC}})_{\ast }(\unicode[STIX]{x1D707}_{\breve{\unicode[STIX]{x1D6FC}}}\times \widetilde{C}_{\unicode[STIX]{x1D6FC}})\biggr)^{\text{W}}\rightarrow 1.\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow J\rightarrow J^{1}\rightarrow \unicode[STIX]{x1D70B}_{\ast }\biggl(\bigoplus _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}}(i_{\unicode[STIX]{x1D6FC}})_{\ast }(\unicode[STIX]{x1D707}_{\breve{\unicode[STIX]{x1D6FC}}}\times \widetilde{C}_{\unicode[STIX]{x1D6FC}})\biggr)^{\text{W}}\rightarrow 1.\end{eqnarray}$$
As a result, we obtain a short exact sequence of Picard stacks (see §A.2)
 $$\begin{eqnarray}1\rightarrow \biggl(\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}}\operatorname{Res}_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}/B}(\unicode[STIX]{x1D707}_{\breve{\unicode[STIX]{x1D6FC}}}\times \widetilde{C}_{\unicode[STIX]{x1D6FC}})\biggr)^{\text{W}}\rightarrow \mathscr{P}\rightarrow \mathscr{P}^{1}\rightarrow 1.\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow \biggl(\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}}\operatorname{Res}_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}/B}(\unicode[STIX]{x1D707}_{\breve{\unicode[STIX]{x1D6FC}}}\times \widetilde{C}_{\unicode[STIX]{x1D6FC}})\biggr)^{\text{W}}\rightarrow \mathscr{P}\rightarrow \mathscr{P}^{1}\rightarrow 1.\end{eqnarray}$$
To simplify the notation, we will denote
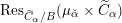 $\operatorname{Res}_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}/B}(\unicode[STIX]{x1D707}_{\breve{\unicode[STIX]{x1D6FC}}}\times \widetilde{C}_{\unicode[STIX]{x1D6FC}})$
by
$\operatorname{Res}_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}/B}(\unicode[STIX]{x1D707}_{\breve{\unicode[STIX]{x1D6FC}}}\times \widetilde{C}_{\unicode[STIX]{x1D6FC}})$
by
![]() $\unicode[STIX]{x1D707}_{\breve{\unicode[STIX]{x1D6FC}}}(\widetilde{C}_{\unicode[STIX]{x1D6FC}})$
in what follows.
$\unicode[STIX]{x1D707}_{\breve{\unicode[STIX]{x1D6FC}}}(\widetilde{C}_{\unicode[STIX]{x1D6FC}})$
in what follows.
Consider the composition
 $$\begin{eqnarray}j:\mathscr{P}\rightarrow \mathscr{P}^{1}\rightarrow \operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B).\end{eqnarray}$$
$$\begin{eqnarray}j:\mathscr{P}\rightarrow \mathscr{P}^{1}\rightarrow \operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B).\end{eqnarray}$$
Combining Lemma 3.1.2 and (3.1.4), we recover a description of
![]() $\mathscr{P}$
in terms of
$\mathscr{P}$
in terms of
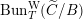 $\operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B)$
as given in [Reference Donagi and GaitsgoryDG02, §16.3]. Namely, given a strongly
$\operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B)$
as given in [Reference Donagi and GaitsgoryDG02, §16.3]. Namely, given a strongly
![]() $\text{W}$
-equivariant
$\text{W}$
-equivariant
![]() $T$
-torsor
$T$
-torsor
![]() $(E_{T},\unicode[STIX]{x1D6FE})$
, one obtains a canonical trivialization
$(E_{T},\unicode[STIX]{x1D6FE})$
, one obtains a canonical trivialization
 $$\begin{eqnarray}E_{T}^{\breve{\unicode[STIX]{x1D6FC}}\circ \unicode[STIX]{x1D6FC}}:=(E_{T}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}})\times ^{T,\unicode[STIX]{x1D6FC}}\mathbb{G}_{m}\times ^{\mathbb{G}_{m},\breve{\unicode[STIX]{x1D6FC}}}T\simeq E_{T}^{0}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}},\end{eqnarray}$$
$$\begin{eqnarray}E_{T}^{\breve{\unicode[STIX]{x1D6FC}}\circ \unicode[STIX]{x1D6FC}}:=(E_{T}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}})\times ^{T,\unicode[STIX]{x1D6FC}}\mathbb{G}_{m}\times ^{\mathbb{G}_{m},\breve{\unicode[STIX]{x1D6FC}}}T\simeq E_{T}^{0}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}},\end{eqnarray}$$
given by
 $(E_{T}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}})\times ^{T,\unicode[STIX]{x1D6FC}}\mathbb{G}_{m}\times ^{\mathbb{G}_{m},\breve{\unicode[STIX]{x1D6FC}}}T\simeq E_{T}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}}\otimes s_{\unicode[STIX]{x1D6FC}}(E_{T}^{-1})|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}}$
. The condition that
$(E_{T}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}})\times ^{T,\unicode[STIX]{x1D6FC}}\mathbb{G}_{m}\times ^{\mathbb{G}_{m},\breve{\unicode[STIX]{x1D6FC}}}T\simeq E_{T}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}}\otimes s_{\unicode[STIX]{x1D6FC}}(E_{T}^{-1})|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}}$
. The condition that
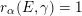 $r_{\unicode[STIX]{x1D6FC}}(E,\unicode[STIX]{x1D6FE})=1$
is equivalent to the condition that (3.1.5) comes from a trivialization
$r_{\unicode[STIX]{x1D6FC}}(E,\unicode[STIX]{x1D6FE})=1$
is equivalent to the condition that (3.1.5) comes from a trivialization
 $$\begin{eqnarray}c_{\unicode[STIX]{x1D6FC}}:E_{T}^{\unicode[STIX]{x1D6FC}}:=(E_{T}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}})\times ^{T,\unicode[STIX]{x1D6FC}}\mathbb{G}_{m}\simeq \mathbb{G}_{m}\times \widetilde{C}_{\unicode[STIX]{x1D6FC}}.\end{eqnarray}$$
$$\begin{eqnarray}c_{\unicode[STIX]{x1D6FC}}:E_{T}^{\unicode[STIX]{x1D6FC}}:=(E_{T}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}})\times ^{T,\unicode[STIX]{x1D6FC}}\mathbb{G}_{m}\simeq \mathbb{G}_{m}\times \widetilde{C}_{\unicode[STIX]{x1D6FC}}.\end{eqnarray}$$
In addition, the set of all such
![]() $c_{\unicode[STIX]{x1D6FC}}$
form a
$c_{\unicode[STIX]{x1D6FC}}$
form a
![]() $\unicode[STIX]{x1D707}_{\breve{\unicode[STIX]{x1D6FC}}}$
-torsor. Consider the following Picard stack
$\unicode[STIX]{x1D707}_{\breve{\unicode[STIX]{x1D6FC}}}$
-torsor. Consider the following Picard stack
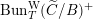 $\operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B)^{+}$
: for any
$\operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B)^{+}$
: for any
![]() $B$
-scheme
$B$
-scheme
![]() $S$
, its
$S$
, its
![]() $S$
-points form the Picard groupoid of triples
$S$
-points form the Picard groupoid of triples
 $$\begin{eqnarray}\operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}_{S})^{+}:=(E_{T},\unicode[STIX]{x1D6FE},c_{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}_{S})^{+}:=(E_{T},\unicode[STIX]{x1D6FE},c_{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}),\end{eqnarray}$$
where
![]() $(E_{T},\unicode[STIX]{x1D6FE})$
is a strongly
$(E_{T},\unicode[STIX]{x1D6FE})$
is a strongly
![]() $\text{W}$
-equivariant
$\text{W}$
-equivariant
![]() $T$
-torsor on
$T$
-torsor on
![]() $\widetilde{C}_{S}$
, and
$\widetilde{C}_{S}$
, and
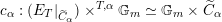 $c_{\unicode[STIX]{x1D6FC}}:(E_{T}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}})\times ^{T,\unicode[STIX]{x1D6FC}}\mathbb{G}_{m}\simeq \mathbb{G}_{m}\times \widetilde{C}_{\unicode[STIX]{x1D6FC}}$
is a trivialization, which induces (3.1.5) and is compatible with the
$c_{\unicode[STIX]{x1D6FC}}:(E_{T}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}})\times ^{T,\unicode[STIX]{x1D6FC}}\mathbb{G}_{m}\simeq \mathbb{G}_{m}\times \widetilde{C}_{\unicode[STIX]{x1D6FC}}$
is a trivialization, which induces (3.1.5) and is compatible with the
![]() $\text{W}$
-equivariant structure. We call those trivializations
$\text{W}$
-equivariant structure. We call those trivializations
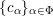 $\{c_{\unicode[STIX]{x1D6FC}}\}_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}}$
a
$\{c_{\unicode[STIX]{x1D6FC}}\}_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}}$
a
![]() $+$
-structure on
$+$
-structure on
![]() $(E_{T},\unicode[STIX]{x1D6FE})$
. Note that, by Lemma 3.1.2, we have the following short exact sequence of Picard stacks:
$(E_{T},\unicode[STIX]{x1D6FE})$
. Note that, by Lemma 3.1.2, we have the following short exact sequence of Picard stacks:
 $$\begin{eqnarray}1\rightarrow \biggl(\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}}\operatorname{Res}_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}/B}(\unicode[STIX]{x1D707}_{\breve{\unicode[STIX]{x1D6FC}}}\times \widetilde{C}_{\unicode[STIX]{x1D6FC}})\biggr)^{\text{W}}\rightarrow \operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B)^{+}\rightarrow \mathscr{P}^{1}\rightarrow 1.\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow \biggl(\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}}\operatorname{Res}_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}/B}(\unicode[STIX]{x1D707}_{\breve{\unicode[STIX]{x1D6FC}}}\times \widetilde{C}_{\unicode[STIX]{x1D6FC}})\biggr)^{\text{W}}\rightarrow \operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B)^{+}\rightarrow \mathscr{P}^{1}\rightarrow 1.\end{eqnarray}$$
Lemma 3.1.3 [Reference Donagi and GaitsgoryDG02, Proposition 16.4].
We have
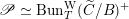 $\mathscr{P}\simeq \operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B)^{+}$
.
$\mathscr{P}\simeq \operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B)^{+}$
.
Proof. Indeed, the exact sequence (3.1.3) implies that, for any
![]() $J$
-torsor
$J$
-torsor
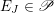 $E_{J}\in \mathscr{P}$
the image
$E_{J}\in \mathscr{P}$
the image
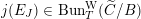 $j(E_{J})\in \operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B)$
carries a canonical
$j(E_{J})\in \operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B)$
carries a canonical
![]() $+$
-structure. This defines a morphism
$+$
-structure. This defines a morphism
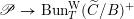 $\mathscr{P}\rightarrow \operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B)^{+}$
and one can check that it is compatible with the short exact sequences (3.1.4) and (3.1.8). The lemma follows.◻
$\mathscr{P}\rightarrow \operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B)^{+}$
and one can check that it is compatible with the short exact sequences (3.1.4) and (3.1.8). The lemma follows.◻
Here is an application of the above discussion. Observe there is the norm map
 $$\begin{eqnarray}\operatorname{Nm}:\operatorname{Bun}_{T}(\widetilde{C}/B)\rightarrow \operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B),\quad E_{T}\mapsto \biggl(\bigotimes _{w\in W}w(E_{T}),\unicode[STIX]{x1D6FE}_{\text{can}}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Nm}:\operatorname{Bun}_{T}(\widetilde{C}/B)\rightarrow \operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B),\quad E_{T}\mapsto \biggl(\bigotimes _{w\in W}w(E_{T}),\unicode[STIX]{x1D6FE}_{\text{can}}\biggr).\end{eqnarray}$$
We claim that
![]() $\operatorname{Nm}$
admits a canonical lifting
$\operatorname{Nm}$
admits a canonical lifting
 $$\begin{eqnarray}\operatorname{Nm}^{\mathscr{P}}:\operatorname{Bun}_{T}(\widetilde{C}/B)\rightarrow \mathscr{P}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Nm}^{\mathscr{P}}:\operatorname{Bun}_{T}(\widetilde{C}/B)\rightarrow \mathscr{P}.\end{eqnarray}$$
To show this, we need to exhibit a canonical trivialization
 $$\begin{eqnarray}c_{\unicode[STIX]{x1D6FC}}:\bigotimes _{w\in \text{W}}w(E_{T})|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}}\times ^{T,\unicode[STIX]{x1D6FC}}\mathbb{G}_{m}\simeq \mathbb{G}_{m}\times \widetilde{C}_{\unicode[STIX]{x1D6FC}}\end{eqnarray}$$
$$\begin{eqnarray}c_{\unicode[STIX]{x1D6FC}}:\bigotimes _{w\in \text{W}}w(E_{T})|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}}\times ^{T,\unicode[STIX]{x1D6FC}}\mathbb{G}_{m}\simeq \mathbb{G}_{m}\times \widetilde{C}_{\unicode[STIX]{x1D6FC}}\end{eqnarray}$$
compatible with the strongly
![]() $\text{W}$
-equivariant structure. However, for any
$\text{W}$
-equivariant structure. However, for any
![]() $T$
-torsor
$T$
-torsor
![]() $E_{T}$
, there is a canonical isomorphism
$E_{T}$
, there is a canonical isomorphism
 $(E_{T}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}}\otimes s_{\unicode[STIX]{x1D6FC}}(E_{T})|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}})\times ^{T,\unicode[STIX]{x1D6FC}}\mathbb{G}_{m}\simeq \mathbb{G}_{m}\times \widetilde{C}_{\unicode[STIX]{x1D6FC}}$
, and therefore, we obtain
$(E_{T}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}}\otimes s_{\unicode[STIX]{x1D6FC}}(E_{T})|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}})\times ^{T,\unicode[STIX]{x1D6FC}}\mathbb{G}_{m}\simeq \mathbb{G}_{m}\times \widetilde{C}_{\unicode[STIX]{x1D6FC}}$
, and therefore, we obtain
![]() $c_{\unicode[STIX]{x1D6FC}}$
by writing
$c_{\unicode[STIX]{x1D6FC}}$
by writing
 $$\begin{eqnarray}\bigotimes _{w\in W}w(E_{T})|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}}\times ^{T,\unicode[STIX]{x1D6FC}}\mathbb{G}_{m}\simeq \bigotimes _{w\in s_{\unicode[STIX]{x1D6FC}}\setminus W}(w(E_{T})|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}}\otimes s_{\unicode[STIX]{x1D6FC}}w(E_{T})|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}})\times ^{T,\unicode[STIX]{x1D6FC}}\mathbb{G}_{m},\end{eqnarray}$$
$$\begin{eqnarray}\bigotimes _{w\in W}w(E_{T})|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}}\times ^{T,\unicode[STIX]{x1D6FC}}\mathbb{G}_{m}\simeq \bigotimes _{w\in s_{\unicode[STIX]{x1D6FC}}\setminus W}(w(E_{T})|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}}\otimes s_{\unicode[STIX]{x1D6FC}}w(E_{T})|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}})\times ^{T,\unicode[STIX]{x1D6FC}}\mathbb{G}_{m},\end{eqnarray}$$
where
![]() $s_{\unicode[STIX]{x1D6FC}}\setminus W$
denotes the quotient of
$s_{\unicode[STIX]{x1D6FC}}\setminus W$
denotes the quotient of
![]() $W$
by the subgroup generated by
$W$
by the subgroup generated by
![]() $s_{\unicode[STIX]{x1D6FC}}$
. The compatibility of the collection
$s_{\unicode[STIX]{x1D6FC}}$
. The compatibility of the collection
![]() $\{c_{\unicode[STIX]{x1D6FC}}\}$
with the
$\{c_{\unicode[STIX]{x1D6FC}}\}$
with the
![]() $\text{W}$
-equivariant structure is clear.
$\text{W}$
-equivariant structure is clear.
3.2 Galois description of
 $\mathscr{P}$
-torsors
$\mathscr{P}$
-torsors
The above description of
![]() $\mathscr{P}$
in terms of
$\mathscr{P}$
in terms of
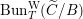 $\operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B)$
can be generalized as follows. Let
$\operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B)$
can be generalized as follows. Let
![]() $\mathscr{D}$
be a
$\mathscr{D}$
be a
![]() $J$
-gerbe on
$J$
-gerbe on
![]() $C\times B$
. Similarly to (3.1.2), we define
$C\times B$
. Similarly to (3.1.2), we define
 $$\begin{eqnarray}\mathscr{D}_{T}:=(\unicode[STIX]{x1D70B}^{\ast }\mathscr{D})^{j^{1}}\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{D}_{T}:=(\unicode[STIX]{x1D70B}^{\ast }\mathscr{D})^{j^{1}}\end{eqnarray}$$
as the
![]() $T$
-gerbe on
$T$
-gerbe on
![]() $\widetilde{C}$
induced from
$\widetilde{C}$
induced from
![]() $\mathscr{D}$
using maps
$\mathscr{D}$
using maps
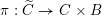 $\unicode[STIX]{x1D70B}:\widetilde{C}\rightarrow C\times B$
and
$\unicode[STIX]{x1D70B}:\widetilde{C}\rightarrow C\times B$
and
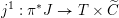 $j^{1}:\unicode[STIX]{x1D70B}^{\ast }J\rightarrow T\times \widetilde{C}$
(see §A.5 and §A.6 for the notion of gerbes and functors between them). Since the map
$j^{1}:\unicode[STIX]{x1D70B}^{\ast }J\rightarrow T\times \widetilde{C}$
(see §A.5 and §A.6 for the notion of gerbes and functors between them). Since the map
![]() $j^{1}$
is
$j^{1}$
is
![]() $\text{W}$
-equivariant the gerbe
$\text{W}$
-equivariant the gerbe
![]() $\mathscr{D}_{T}$
is strongly
$\mathscr{D}_{T}$
is strongly
![]() $\text{W}$
-equivariant. Equivalently, this means that
$\text{W}$
-equivariant. Equivalently, this means that
![]() $\mathscr{D}_{T}$
descends to a
$\mathscr{D}_{T}$
descends to a
![]() ${\mathcal{T}}$
-gerbe on
${\mathcal{T}}$
-gerbe on
![]() $[\widetilde{C}/\text{W}]$
.
$[\widetilde{C}/\text{W}]$
.
Let
![]() $\mathscr{T}_{\mathscr{D}}$
be the stack of splittings of
$\mathscr{T}_{\mathscr{D}}$
be the stack of splittings of
![]() $\mathscr{D}$
over
$\mathscr{D}$
over
![]() $B$
. By definition, for every
$B$
. By definition, for every
![]() $S\rightarrow B$
,
$S\rightarrow B$
,
![]() $\mathscr{T}_{\mathscr{D}}(S)$
is the groupoid of the splittings of the gerbe
$\mathscr{T}_{\mathscr{D}}(S)$
is the groupoid of the splittings of the gerbe
![]() $\mathscr{D}|_{C\times S}$
. This is a (pseudo)
$\mathscr{D}|_{C\times S}$
. This is a (pseudo)
![]() $\mathscr{P}$
-torsor. On the other hand, let
$\mathscr{P}$
-torsor. On the other hand, let
![]() $\mathscr{T}_{\mathscr{D}_{T}}^{\text{W}}$
denote the stack of strongly
$\mathscr{T}_{\mathscr{D}_{T}}^{\text{W}}$
denote the stack of strongly
![]() $\text{W}$
-equivariant splittings of
$\text{W}$
-equivariant splittings of
![]() $\mathscr{D}_{T}$
, i.e.,
$\mathscr{D}_{T}$
, i.e.,
![]() $\mathscr{T}_{\mathscr{D}_{T}}^{\text{W}}(S)$
is the groupoid of the splittings of
$\mathscr{T}_{\mathscr{D}_{T}}^{\text{W}}(S)$
is the groupoid of the splittings of
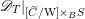 $\mathscr{D}_{T}|_{[\widetilde{C}/\text{W}]\times _{B}S}$
. Our goal is to give a description of
$\mathscr{D}_{T}|_{[\widetilde{C}/\text{W}]\times _{B}S}$
. Our goal is to give a description of
![]() $\mathscr{T}_{\mathscr{D}}$
in terms of
$\mathscr{T}_{\mathscr{D}}$
in terms of
![]() $\mathscr{T}_{\mathscr{D}_{T}}^{\text{W}}$
.
$\mathscr{T}_{\mathscr{D}_{T}}^{\text{W}}$
.
Let
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}$
. Similarly to
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}$
. Similarly to
![]() $E_{T}^{\unicode[STIX]{x1D6FC}}$
and
$E_{T}^{\unicode[STIX]{x1D6FC}}$
and
![]() $E_{T}^{\breve{\unicode[STIX]{x1D6FC}}\circ \unicode[STIX]{x1D6FC}}$
as defined in (3.1.5) and (3.1.6), let
$E_{T}^{\breve{\unicode[STIX]{x1D6FC}}\circ \unicode[STIX]{x1D6FC}}$
as defined in (3.1.5) and (3.1.6), let
![]() $\mathscr{D}_{T}^{\unicode[STIX]{x1D6FC}}$
,
$\mathscr{D}_{T}^{\unicode[STIX]{x1D6FC}}$
,
![]() $\mathscr{D}_{T}^{\breve{\unicode[STIX]{x1D6FC}}\circ \unicode[STIX]{x1D6FC}}$
denote the restrictions to
$\mathscr{D}_{T}^{\breve{\unicode[STIX]{x1D6FC}}\circ \unicode[STIX]{x1D6FC}}$
denote the restrictions to
![]() $\widetilde{C}_{\unicode[STIX]{x1D6FC}}$
of the
$\widetilde{C}_{\unicode[STIX]{x1D6FC}}$
of the
![]() $\mathbb{G}_{m}$
- and
$\mathbb{G}_{m}$
- and
![]() $T$
-gerbes on
$T$
-gerbes on
![]() $\widetilde{C}$
induced from
$\widetilde{C}$
induced from
![]() $\mathscr{D}_{T}$
using the maps
$\mathscr{D}_{T}$
using the maps
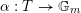 $\unicode[STIX]{x1D6FC}:T\rightarrow \mathbb{G}_{m}$
and
$\unicode[STIX]{x1D6FC}:T\rightarrow \mathbb{G}_{m}$
and
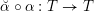 $\breve{\unicode[STIX]{x1D6FC}}\circ \unicode[STIX]{x1D6FC}:T\rightarrow T$
respectively. The strongly
$\breve{\unicode[STIX]{x1D6FC}}\circ \unicode[STIX]{x1D6FC}:T\rightarrow T$
respectively. The strongly
![]() $\text{W}$
-equivariant structure on
$\text{W}$
-equivariant structure on
![]() $\mathscr{D}_{T}$
implies that the
$\mathscr{D}_{T}$
implies that the
![]() $T$
-gerbe
$T$
-gerbe
![]() $\mathscr{D}_{T}^{\breve{\unicode[STIX]{x1D6FC}}\circ \unicode[STIX]{x1D6FC}}$
has a canonical splitting
$\mathscr{D}_{T}^{\breve{\unicode[STIX]{x1D6FC}}\circ \unicode[STIX]{x1D6FC}}$
has a canonical splitting
![]() $F_{\unicode[STIX]{x1D6FC}}^{0}$
. Moreover, by a similar argument in §3.1, one can show that: (i) there is a canonical splitting
$F_{\unicode[STIX]{x1D6FC}}^{0}$
. Moreover, by a similar argument in §3.1, one can show that: (i) there is a canonical splitting
![]() $E_{\unicode[STIX]{x1D6FC}}^{0}$
of the
$E_{\unicode[STIX]{x1D6FC}}^{0}$
of the
![]() $\mathbb{G}_{m}$
-gerbe
$\mathbb{G}_{m}$
-gerbe
![]() $\mathscr{D}_{T}^{\unicode[STIX]{x1D6FC}}$
, which induces
$\mathscr{D}_{T}^{\unicode[STIX]{x1D6FC}}$
, which induces
![]() $F_{\unicode[STIX]{x1D6FC}}^{0}$
via the canonical map
$F_{\unicode[STIX]{x1D6FC}}^{0}$
via the canonical map
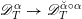 $\mathscr{D}_{T}^{\unicode[STIX]{x1D6FC}}\rightarrow \mathscr{D}_{T}^{\breve{\unicode[STIX]{x1D6FC}}\circ \unicode[STIX]{x1D6FC}}$
and: (ii) for any strongly
$\mathscr{D}_{T}^{\unicode[STIX]{x1D6FC}}\rightarrow \mathscr{D}_{T}^{\breve{\unicode[STIX]{x1D6FC}}\circ \unicode[STIX]{x1D6FC}}$
and: (ii) for any strongly
![]() $\text{W}$
-equivariant splitting
$\text{W}$
-equivariant splitting
![]() $(E,\unicode[STIX]{x1D6FE})$
of
$(E,\unicode[STIX]{x1D6FE})$
of
![]() $\mathscr{D}_{T}$
there is a canonical isomorphism of splittings
$\mathscr{D}_{T}$
there is a canonical isomorphism of splittings
 $$\begin{eqnarray}E^{\breve{\unicode[STIX]{x1D6FC}}\circ \unicode[STIX]{x1D6FC}}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}}\simeq F_{\unicode[STIX]{x1D6FC}}^{0},\end{eqnarray}$$
$$\begin{eqnarray}E^{\breve{\unicode[STIX]{x1D6FC}}\circ \unicode[STIX]{x1D6FC}}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}}\simeq F_{\unicode[STIX]{x1D6FC}}^{0},\end{eqnarray}$$
where
![]() $E^{\breve{\unicode[STIX]{x1D6FC}}\circ \unicode[STIX]{x1D6FC}}$
is the splitting of
$E^{\breve{\unicode[STIX]{x1D6FC}}\circ \unicode[STIX]{x1D6FC}}$
is the splitting of
![]() $\mathscr{D}_{T}^{\breve{\unicode[STIX]{x1D6FC}}\circ \unicode[STIX]{x1D6FC}}$
induces by
$\mathscr{D}_{T}^{\breve{\unicode[STIX]{x1D6FC}}\circ \unicode[STIX]{x1D6FC}}$
induces by
![]() $E$
via the canonical map
$E$
via the canonical map
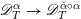 $\mathscr{D}_{T}^{\unicode[STIX]{x1D6FC}}\rightarrow \mathscr{D}_{T}^{\breve{\unicode[STIX]{x1D6FC}}\circ \unicode[STIX]{x1D6FC}}$
. We define
$\mathscr{D}_{T}^{\unicode[STIX]{x1D6FC}}\rightarrow \mathscr{D}_{T}^{\breve{\unicode[STIX]{x1D6FC}}\circ \unicode[STIX]{x1D6FC}}$
. We define
![]() $\mathscr{T}_{\mathscr{D}_{T}}^{\text{W},+}$
as the stack over
$\mathscr{T}_{\mathscr{D}_{T}}^{\text{W},+}$
as the stack over
![]() $B$
whose
$B$
whose
![]() $S$
-points consist of
$S$
-points consist of
 $$\begin{eqnarray}\mathscr{T}_{\mathscr{D}_{T}}^{\text{W},+}(S):=(E,\unicode[STIX]{x1D6FE},t_{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}),\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{T}_{\mathscr{D}_{T}}^{\text{W},+}(S):=(E,\unicode[STIX]{x1D6FE},t_{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}),\end{eqnarray}$$
where
![]() $(E,\unicode[STIX]{x1D6FE})$
is a strongly
$(E,\unicode[STIX]{x1D6FE})$
is a strongly
![]() $\text{W}$
-equivariant splittings of
$\text{W}$
-equivariant splittings of
![]() $\mathscr{D}_{T}$
and
$\mathscr{D}_{T}$
and
 $$\begin{eqnarray}t_{\unicode[STIX]{x1D6FC}}:E^{\unicode[STIX]{x1D6FC}}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}}\simeq E_{\unicode[STIX]{x1D6FC}}^{0}\end{eqnarray}$$
$$\begin{eqnarray}t_{\unicode[STIX]{x1D6FC}}:E^{\unicode[STIX]{x1D6FC}}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}}\simeq E_{\unicode[STIX]{x1D6FC}}^{0}\end{eqnarray}$$
is an isomorphism of splittings of
![]() $\mathscr{D}_{T}^{\unicode[STIX]{x1D6FC}}$
, which induces (3.2.1) and is compatible with the
$\mathscr{D}_{T}^{\unicode[STIX]{x1D6FC}}$
, which induces (3.2.1) and is compatible with the
![]() $\text{W}$
-equivariant structure. It is clear that
$\text{W}$
-equivariant structure. It is clear that
![]() $\mathscr{T}_{\mathscr{D}_{T}}^{\text{W},+}$
is a
$\mathscr{T}_{\mathscr{D}_{T}}^{\text{W},+}$
is a
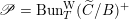 $\mathscr{P}=\operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B)^{+}$
-torsor.
$\mathscr{P}=\operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B)^{+}$
-torsor.
Lemma 3.2.1. There is a canonical isomorphism of
![]() $\mathscr{P}$
-torsors
$\mathscr{P}$
-torsors
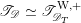 $\mathscr{T}_{\mathscr{D}}\simeq \mathscr{T}_{\mathscr{D}_{T}}^{\text{W},+}$
.
$\mathscr{T}_{\mathscr{D}}\simeq \mathscr{T}_{\mathscr{D}_{T}}^{\text{W},+}$
.
Proof. Let
 $E\in \mathscr{T}_{\mathscr{D}}$
be a splitting of
$E\in \mathscr{T}_{\mathscr{D}}$
be a splitting of
![]() $\mathscr{D}$
. Then
$\mathscr{D}$
. Then
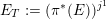 $E_{T}:=(\unicode[STIX]{x1D70B}^{\ast }(E))^{j^{1}}$
defines a splitting of
$E_{T}:=(\unicode[STIX]{x1D70B}^{\ast }(E))^{j^{1}}$
defines a splitting of
![]() $\mathscr{D}_{T}$
. Since both maps
$\mathscr{D}_{T}$
. Since both maps
![]() $j^{1}$
and
$j^{1}$
and
![]() $\unicode[STIX]{x1D70B}$
are
$\unicode[STIX]{x1D70B}$
are
![]() $\text{W}$
-equivariant the splitting
$\text{W}$
-equivariant the splitting
![]() $E_{T}$
has a canonical
$E_{T}$
has a canonical
![]() $\text{W}$
-equivariant structure, which we denote by
$\text{W}$
-equivariant structure, which we denote by
![]() $\unicode[STIX]{x1D6FE}$
. Moreover, by the same reasoning as in §3.1, there is a canonical isomorphism of splittings
$\unicode[STIX]{x1D6FE}$
. Moreover, by the same reasoning as in §3.1, there is a canonical isomorphism of splittings
 $t_{\unicode[STIX]{x1D6FC}}:E_{T}^{\unicode[STIX]{x1D6FC}}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}}\simeq E_{\unicode[STIX]{x1D6FC}}^{0}$
such that the induced isomorphism
$t_{\unicode[STIX]{x1D6FC}}:E_{T}^{\unicode[STIX]{x1D6FC}}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}}\simeq E_{\unicode[STIX]{x1D6FC}}^{0}$
such that the induced isomorphism
 $E_{T}^{\breve{\unicode[STIX]{x1D6FC}}\circ \unicode[STIX]{x1D6FC}}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}}\stackrel{}{\simeq }(E_{\unicode[STIX]{x1D6FC}}^{0})^{\unicode[STIX]{x1D6FC}}\simeq F_{\unicode[STIX]{x1D6FC}}^{0}$
is equal to the one coming from the
$E_{T}^{\breve{\unicode[STIX]{x1D6FC}}\circ \unicode[STIX]{x1D6FC}}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}}\stackrel{}{\simeq }(E_{\unicode[STIX]{x1D6FC}}^{0})^{\unicode[STIX]{x1D6FC}}\simeq F_{\unicode[STIX]{x1D6FC}}^{0}$
is equal to the one coming from the
![]() $\text{W}$
-equivariant structure
$\text{W}$
-equivariant structure
![]() $\unicode[STIX]{x1D6FE}$
. The assignment
$\unicode[STIX]{x1D6FE}$
. The assignment
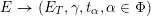 $E\rightarrow (E_{T},\unicode[STIX]{x1D6FE},t_{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7})$
defines a morphism
$E\rightarrow (E_{T},\unicode[STIX]{x1D6FE},t_{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7})$
defines a morphism
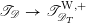 $\mathscr{T}_{\mathscr{D}}\rightarrow \mathscr{T}_{\mathscr{D}_{T}}^{\text{W},+}$
, which is compatible with their
$\mathscr{T}_{\mathscr{D}}\rightarrow \mathscr{T}_{\mathscr{D}_{T}}^{\text{W},+}$
, which is compatible with their
![]() $\mathscr{P}$
-torsor structures and hence is an isomorphism.◻
$\mathscr{P}$
-torsor structures and hence is an isomorphism.◻
3.3 The Abel–Jacobi map
From now on till the end of this section, we restrict to the open subset
![]() $B^{0}$
of the Hitchin base. To simplify the notations, we use
$B^{0}$
of the Hitchin base. To simplify the notations, we use
![]() $B$
to denote
$B$
to denote
![]() $B^{0}$
unless specified. Recall from Proposition 2.6.1 that the cameral curve
$B^{0}$
unless specified. Recall from Proposition 2.6.1 that the cameral curve
![]() $\widetilde{C}$
is smooth over
$\widetilde{C}$
is smooth over
![]() $B^{0}$
.
$B^{0}$
.
Let
 $$\begin{eqnarray}\operatorname{AJ}:\widetilde{C}\times \mathbb{X}_{\bullet }(T)\rightarrow \operatorname{Bun}_{T}(\widetilde{C}/B)\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{AJ}:\widetilde{C}\times \mathbb{X}_{\bullet }(T)\rightarrow \operatorname{Bun}_{T}(\widetilde{C}/B)\end{eqnarray}$$
be the Abel–Jacobi map given by
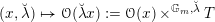 $(x,\breve{\unicode[STIX]{x1D706}})\mapsto {\mathcal{O}}(\breve{\unicode[STIX]{x1D706}}x):={\mathcal{O}}(x)\times ^{\mathbb{G}_{m},\breve{\unicode[STIX]{x1D706}}}T$
. By composition with
$(x,\breve{\unicode[STIX]{x1D706}})\mapsto {\mathcal{O}}(\breve{\unicode[STIX]{x1D706}}x):={\mathcal{O}}(x)\times ^{\mathbb{G}_{m},\breve{\unicode[STIX]{x1D706}}}T$
. By composition with
![]() $\operatorname{Nm}^{\mathscr{P}}$
, we obtain a morphism
$\operatorname{Nm}^{\mathscr{P}}$
, we obtain a morphism
 $$\begin{eqnarray}\operatorname{AJ}^{\mathscr{P}}:\widetilde{C}\times \mathbb{X}_{\bullet }(T)\rightarrow \mathscr{P}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{AJ}^{\mathscr{P}}:\widetilde{C}\times \mathbb{X}_{\bullet }(T)\rightarrow \mathscr{P}.\end{eqnarray}$$
It is
![]() $\text{W}$
-equivariant, where
$\text{W}$
-equivariant, where
![]() $\text{W}$
acts on
$\text{W}$
acts on
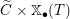 $\widetilde{C}\times \mathbb{X}_{\bullet }(T)$
diagonally and on
$\widetilde{C}\times \mathbb{X}_{\bullet }(T)$
diagonally and on
![]() $\mathscr{P}$
trivially, and is commutative and multiplicative with respect to the group structures on
$\mathscr{P}$
trivially, and is commutative and multiplicative with respect to the group structures on
![]() $\mathbb{X}_{\bullet }(T)$
and on
$\mathbb{X}_{\bullet }(T)$
and on
![]() $\mathscr{P}$
. Observe that for any
$\mathscr{P}$
. Observe that for any
![]() $x\in \widetilde{C}_{\unicode[STIX]{x1D6FC}}$
,
$x\in \widetilde{C}_{\unicode[STIX]{x1D6FC}}$
,
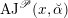 $\operatorname{AJ}^{\mathscr{P}}(x,\breve{\unicode[STIX]{x1D6FC}})$
is the unit in
$\operatorname{AJ}^{\mathscr{P}}(x,\breve{\unicode[STIX]{x1D6FC}})$
is the unit in
![]() $\mathscr{P}$
. This follows from
$\mathscr{P}$
. This follows from
 $$\begin{eqnarray}\bigotimes _{w\in W}w{\mathcal{O}}(\breve{\unicode[STIX]{x1D6FC}}x)\simeq \bigotimes _{w\in W/s_{\unicode[STIX]{x1D6FC}}}w{\mathcal{O}}(\breve{\unicode[STIX]{x1D6FC}}x+s_{\unicode[STIX]{x1D6FC}}(\breve{\unicode[STIX]{x1D6FC}})x)\end{eqnarray}$$
$$\begin{eqnarray}\bigotimes _{w\in W}w{\mathcal{O}}(\breve{\unicode[STIX]{x1D6FC}}x)\simeq \bigotimes _{w\in W/s_{\unicode[STIX]{x1D6FC}}}w{\mathcal{O}}(\breve{\unicode[STIX]{x1D6FC}}x+s_{\unicode[STIX]{x1D6FC}}(\breve{\unicode[STIX]{x1D6FC}})x)\end{eqnarray}$$
being canonically trivialized, and the trivialization is compatible with the
![]() $\text{W}$
-equivariant structure. Here, as before,
$\text{W}$
-equivariant structure. Here, as before,
![]() $W/s_{\unicode[STIX]{x1D6FC}}$
is the quotient of
$W/s_{\unicode[STIX]{x1D6FC}}$
is the quotient of
![]() $W$
by the subgroup generated by
$W$
by the subgroup generated by
![]() $s_{\unicode[STIX]{x1D6FC}}$
.
$s_{\unicode[STIX]{x1D6FC}}$
.
By pulling back the line bundles, we thus obtain
 $$\begin{eqnarray}(\operatorname{AJ}^{\mathscr{P}})^{\vee }:\mathscr{P}^{\vee }\rightarrow \operatorname{Pic}\,^{m}(\widetilde{C}\times \mathbb{X}_{\bullet }(T))^{\text{W}},\end{eqnarray}$$
$$\begin{eqnarray}(\operatorname{AJ}^{\mathscr{P}})^{\vee }:\mathscr{P}^{\vee }\rightarrow \operatorname{Pic}\,^{m}(\widetilde{C}\times \mathbb{X}_{\bullet }(T))^{\text{W}},\end{eqnarray}$$
where
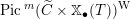 $\operatorname{Pic}\,^{m}(\widetilde{C}\times \mathbb{X}_{\bullet }(T))^{\text{W}}$
denotes the Picard stack over
$\operatorname{Pic}\,^{m}(\widetilde{C}\times \mathbb{X}_{\bullet }(T))^{\text{W}}$
denotes the Picard stack over
![]() $B$
of
$B$
of
![]() $\text{W}$
-equivariant line bundles on
$\text{W}$
-equivariant line bundles on
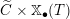 $\widetilde{C}\times \mathbb{X}_{\bullet }(T)$
which are multiplicative with respect to
$\widetilde{C}\times \mathbb{X}_{\bullet }(T)$
which are multiplicative with respect to
![]() $\mathbb{X}_{\bullet }(T)$
. Observe that there is the canonical isomorphism
$\mathbb{X}_{\bullet }(T)$
. Observe that there is the canonical isomorphism
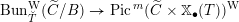 $\operatorname{Bun}_{\breve{T}}^{\text{W}}(\widetilde{C}/B)\rightarrow \operatorname{Pic}\,^{m}(\widetilde{C}\times \mathbb{X}_{\bullet }(T))^{\text{W}}$
given by
$\operatorname{Bun}_{\breve{T}}^{\text{W}}(\widetilde{C}/B)\rightarrow \operatorname{Pic}\,^{m}(\widetilde{C}\times \mathbb{X}_{\bullet }(T))^{\text{W}}$
given by
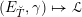 $(E_{\breve{T}},\unicode[STIX]{x1D6FE})\mapsto {\mathcal{L}}$
, where
$(E_{\breve{T}},\unicode[STIX]{x1D6FE})\mapsto {\mathcal{L}}$
, where
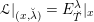 ${\mathcal{L}}|_{(x,\breve{\unicode[STIX]{x1D706}})}=E_{\breve{T}}^{\unicode[STIX]{x1D706}}|_{x}$
. Therefore, we can regard
${\mathcal{L}}|_{(x,\breve{\unicode[STIX]{x1D706}})}=E_{\breve{T}}^{\unicode[STIX]{x1D706}}|_{x}$
. Therefore, we can regard
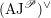 $(\operatorname{AJ}^{\mathscr{P}})^{\vee }$
as a morphism
$(\operatorname{AJ}^{\mathscr{P}})^{\vee }$
as a morphism
 $$\begin{eqnarray}(\operatorname{AJ}^{\mathscr{P}})^{\vee }:\mathscr{P}^{\vee }\rightarrow \operatorname{Bun}_{\breve{T}}^{\text{W}}(\widetilde{C}/B).\end{eqnarray}$$
$$\begin{eqnarray}(\operatorname{AJ}^{\mathscr{P}})^{\vee }:\mathscr{P}^{\vee }\rightarrow \operatorname{Bun}_{\breve{T}}^{\text{W}}(\widetilde{C}/B).\end{eqnarray}$$
We claim that
 $(\operatorname{AJ}^{\mathscr{P}})^{\vee }$
canonically lifts to a morphism
$(\operatorname{AJ}^{\mathscr{P}})^{\vee }$
canonically lifts to a morphism
 $$\begin{eqnarray}\mathfrak{D}_{\text{cl}}:\mathscr{P}^{\vee }\rightarrow \breve{\mathscr{P}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{D}_{\text{cl}}:\mathscr{P}^{\vee }\rightarrow \breve{\mathscr{P}}.\end{eqnarray}$$
Let
![]() ${\mathcal{L}}$
be a multiplicative line bundle on
${\mathcal{L}}$
be a multiplicative line bundle on
![]() $\mathscr{P}$
. We thus need to show that
$\mathscr{P}$
. We thus need to show that
 $$\begin{eqnarray}(\operatorname{AJ}^{\mathscr{P}})^{\ast }{\mathcal{L}}|_{(\widetilde{C}_{\unicode[STIX]{x1D6FC}},\breve{\unicode[STIX]{x1D6FC}})}\end{eqnarray}$$
$$\begin{eqnarray}(\operatorname{AJ}^{\mathscr{P}})^{\ast }{\mathcal{L}}|_{(\widetilde{C}_{\unicode[STIX]{x1D6FC}},\breve{\unicode[STIX]{x1D6FC}})}\end{eqnarray}$$
admits a canonical trivialization, which is compatible with the
![]() $\text{W}$
-equivariance structure. However, this follows from
$\text{W}$
-equivariance structure. However, this follows from
 $\operatorname{AJ}^{\mathscr{P}}((x,\breve{\unicode[STIX]{x1D6FC}}))$
is the unit of
$\operatorname{AJ}^{\mathscr{P}}((x,\breve{\unicode[STIX]{x1D6FC}}))$
is the unit of
![]() $\mathscr{P}$
and a multiplicative line bundle on
$\mathscr{P}$
and a multiplicative line bundle on
![]() $\mathscr{P}$
is canonically trivialized over the unit. To summarize, we have constructed the following commutative diagram.
$\mathscr{P}$
is canonically trivialized over the unit. To summarize, we have constructed the following commutative diagram.

Now, the classical duality theorem reads as follows.
Theorem 3.3.1. The morphism
![]() $\mathfrak{D}_{\text{cl}}$
is an isomorphism.
$\mathfrak{D}_{\text{cl}}$
is an isomorphism.
3.4 First reductions
We first show that
![]() $\mathfrak{D}_{\text{cl}}$
induces an isomorphism
$\mathfrak{D}_{\text{cl}}$
induces an isomorphism
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{0}(\mathfrak{D}_{\text{cl}}):\unicode[STIX]{x1D70B}_{0}(\mathscr{P}^{\vee })\rightarrow \unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{0}(\mathfrak{D}_{\text{cl}}):\unicode[STIX]{x1D70B}_{0}(\mathscr{P}^{\vee })\rightarrow \unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}}).\end{eqnarray}$$
For any
![]() $S$
-point
$S$
-point
![]() $b\in B^{0}$
,
$b\in B^{0}$
,
![]() $\mathscr{P}_{b}$
is a Beilinson
$\mathscr{P}_{b}$
is a Beilinson
![]() $1$
-motive (Appendix A). We have
$1$
-motive (Appendix A). We have
 $$\begin{eqnarray}\text{}\underline{\operatorname{Aut}}(e)\simeq \text{H}^{0}(C,J_{b}),\quad \unicode[STIX]{x1D70B}_{0}(\mathscr{P}_{b})=\mathscr{P}_{b}/W_{1}\mathscr{P}_{b}.\end{eqnarray}$$
$$\begin{eqnarray}\text{}\underline{\operatorname{Aut}}(e)\simeq \text{H}^{0}(C,J_{b}),\quad \unicode[STIX]{x1D70B}_{0}(\mathscr{P}_{b})=\mathscr{P}_{b}/W_{1}\mathscr{P}_{b}.\end{eqnarray}$$
Observe that
 $$\begin{eqnarray}\text{H}^{0}(C,J_{b})\simeq \ker \biggl(T^{\text{W}}\rightarrow \biggl(\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}}\operatorname{Res}_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}/b}(\unicode[STIX]{x1D707}_{\breve{\unicode[STIX]{x1D6FC}}}\times \widetilde{C}_{\unicode[STIX]{x1D6FC}})\biggr)^{\text{W}}\biggr)=Z(G).\end{eqnarray}$$
$$\begin{eqnarray}\text{H}^{0}(C,J_{b})\simeq \ker \biggl(T^{\text{W}}\rightarrow \biggl(\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}}\operatorname{Res}_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}/b}(\unicode[STIX]{x1D707}_{\breve{\unicode[STIX]{x1D6FC}}}\times \widetilde{C}_{\unicode[STIX]{x1D6FC}})\biggr)^{\text{W}}\biggr)=Z(G).\end{eqnarray}$$
By Corollary A.4.3
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{0}(\mathscr{P}^{\vee })\simeq (\operatorname{Aut}_{\mathscr{ P}}(e))^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{0}(\mathscr{P}^{\vee })\simeq (\operatorname{Aut}_{\mathscr{ P}}(e))^{\ast }.\end{eqnarray}$$
Let us also recall the description of
![]() $\unicode[STIX]{x1D70B}_{0}(\mathscr{P})$
as given in [Reference NgôNgô10, §§4.10 and 5.5]. As we restrict
$\unicode[STIX]{x1D70B}_{0}(\mathscr{P})$
as given in [Reference NgôNgô10, §§4.10 and 5.5]. As we restrict
![]() $\mathscr{P}$
to
$\mathscr{P}$
to
![]() $B^{0}$
, the answer is very simple. Namely, the Abel–Jacobi map
$B^{0}$
, the answer is very simple. Namely, the Abel–Jacobi map
 $$\begin{eqnarray}\operatorname{AJ}^{\mathscr{P}}:\widetilde{C}\times \mathbb{X}_{\bullet }(T)\rightarrow \mathscr{P}\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{AJ}^{\mathscr{P}}:\widetilde{C}\times \mathbb{X}_{\bullet }(T)\rightarrow \mathscr{P}\end{eqnarray}$$
induces a surjective map
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{0}(\widetilde{C}\times \mathbb{X}_{\bullet }(T))\simeq \mathbb{X}_{\bullet }(T){\twoheadrightarrow}\unicode[STIX]{x1D70B}_{0}(\mathscr{P}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{0}(\widetilde{C}\times \mathbb{X}_{\bullet }(T))\simeq \mathbb{X}_{\bullet }(T){\twoheadrightarrow}\unicode[STIX]{x1D70B}_{0}(\mathscr{P}),\end{eqnarray}$$
which induces
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{0}(\mathscr{P})^{\ast }\simeq Z(\breve{G})\subset \breve{T}^{\text{W}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{0}(\mathscr{P})^{\ast }\simeq Z(\breve{G})\subset \breve{T}^{\text{W}}.\end{eqnarray}$$
Therefore, as abstract groups,
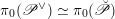 $\unicode[STIX]{x1D70B}_{0}(\mathscr{P}^{\vee })\simeq \unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}})$
.
$\unicode[STIX]{x1D70B}_{0}(\mathscr{P}^{\vee })\simeq \unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}})$
.
Since
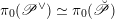 $\unicode[STIX]{x1D70B}_{0}(\mathscr{P}^{\vee })\simeq \unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}})$
are finitely generated abelian groups and are isomorphic abstractly, to show that
$\unicode[STIX]{x1D70B}_{0}(\mathscr{P}^{\vee })\simeq \unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}})$
are finitely generated abelian groups and are isomorphic abstractly, to show that
![]() $\unicode[STIX]{x1D70B}_{0}(\mathfrak{D}_{\text{cl}})$
is an isomorphism, it is enough to show the following.
$\unicode[STIX]{x1D70B}_{0}(\mathfrak{D}_{\text{cl}})$
is an isomorphism, it is enough to show the following.
Lemma 3.4.1. The induced map
![]() $\unicode[STIX]{x1D70B}_{0}(\mathfrak{D}_{\text{cl}})$
is surjective.
$\unicode[STIX]{x1D70B}_{0}(\mathfrak{D}_{\text{cl}})$
is surjective.
Proof. According to the above description, it is enough to construct a morphism
 $\widetilde{C}\times \mathbb{X}^{\bullet }(T)\rightarrow \mathscr{P}^{\vee }$
making the following diagram is commutative.
$\widetilde{C}\times \mathbb{X}^{\bullet }(T)\rightarrow \mathscr{P}^{\vee }$
making the following diagram is commutative.

To this goal, observe that there is the universal line bundle
![]() $\mathscr{L}_{\text{univ}}$
on
$\mathscr{L}_{\text{univ}}$
on
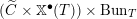 $(\widetilde{C}\times \mathbb{X}^{\bullet }(T))\times \operatorname{Bun}_{T}$
. Then the pullback of this line bundle to
$(\widetilde{C}\times \mathbb{X}^{\bullet }(T))\times \operatorname{Bun}_{T}$
. Then the pullback of this line bundle to
 $(\widetilde{C}\times \mathbb{X}^{\bullet }(T))\times \mathscr{P}$
gives rise to the desired map. The commutativity of this diagram is an easy exercise.◻
$(\widetilde{C}\times \mathbb{X}^{\bullet }(T))\times \mathscr{P}$
gives rise to the desired map. The commutativity of this diagram is an easy exercise.◻
Next, we see that
 $$\begin{eqnarray}W_{0}(\mathfrak{D}_{\text{cl}}):W_{0}\mathscr{P}^{\vee }\rightarrow W_{0}\breve{\mathscr{P}}\end{eqnarray}$$
$$\begin{eqnarray}W_{0}(\mathfrak{D}_{\text{cl}}):W_{0}\mathscr{P}^{\vee }\rightarrow W_{0}\breve{\mathscr{P}}\end{eqnarray}$$
is an isomorphism. Indeed, we can construct
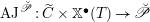 $\operatorname{AJ}^{\breve{\mathscr{P}}}\,:\,\widetilde{C}\times \mathbb{X}^{\bullet }(T)\,\rightarrow \,\breve{\mathscr{P}}$
, and therefore
$\operatorname{AJ}^{\breve{\mathscr{P}}}\,:\,\widetilde{C}\times \mathbb{X}^{\bullet }(T)\,\rightarrow \,\breve{\mathscr{P}}$
, and therefore
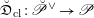 $\breve{\mathfrak{D}}_{\text{cl}}\,:\,\breve{\mathscr{P}}^{\vee }\,\rightarrow \,\mathscr{P}$
. By the same argument, it induces an isomorphism
$\breve{\mathfrak{D}}_{\text{cl}}\,:\,\breve{\mathscr{P}}^{\vee }\,\rightarrow \,\mathscr{P}$
. By the same argument, it induces an isomorphism
 $\unicode[STIX]{x1D70B}_{0}(\breve{\mathfrak{D}}_{\text{cl}}):\unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}}^{\vee })\rightarrow \unicode[STIX]{x1D70B}_{0}(\mathscr{P})$
. It is easy to check that
$\unicode[STIX]{x1D70B}_{0}(\breve{\mathfrak{D}}_{\text{cl}}):\unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}}^{\vee })\rightarrow \unicode[STIX]{x1D70B}_{0}(\mathscr{P})$
. It is easy to check that
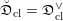 $\breve{\mathfrak{D}}_{\text{cl}}=\mathfrak{D}_{\text{cl}}^{\vee }$
, and therefore
$\breve{\mathfrak{D}}_{\text{cl}}=\mathfrak{D}_{\text{cl}}^{\vee }$
, and therefore
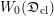 $W_{0}(\mathfrak{D}_{\text{cl}})$
is also an isomorphism.
$W_{0}(\mathfrak{D}_{\text{cl}})$
is also an isomorphism.
Therefore, it is enough to show that
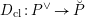 $D_{\text{cl}}\,:\,P^{\vee }\,\rightarrow \,\breve{P}$
is an isomorphism, where
$D_{\text{cl}}\,:\,P^{\vee }\,\rightarrow \,\breve{P}$
is an isomorphism, where
![]() $P$
(respectively
$P$
(respectively
![]() $\breve{P}$
) is the neutral connected component of the coarse moduli space of
$\breve{P}$
) is the neutral connected component of the coarse moduli space of
![]() $\mathscr{P}$
(respectively
$\mathscr{P}$
(respectively
![]() $\breve{\mathscr{P}}$
), and
$\breve{\mathscr{P}}$
), and
![]() $D_{\text{cl}}$
is the map induced by
$D_{\text{cl}}$
is the map induced by
![]() $\mathfrak{D}_{\text{cl}}$
. We can prove this fiberwise, and therefore we fix
$\mathfrak{D}_{\text{cl}}$
. We can prove this fiberwise, and therefore we fix
 $b\in B(k)$
. However, to simplify the notation, in the following discussion we write
$b\in B(k)$
. However, to simplify the notation, in the following discussion we write
![]() $\widetilde{C},\mathscr{P}$
instead of
$\widetilde{C},\mathscr{P}$
instead of
![]() $\widetilde{C}_{b},\mathscr{P}_{b}$
, etc.
$\widetilde{C}_{b},\mathscr{P}_{b}$
, etc.
3.5 The calculation of the coarse moduli
We introduce a few more notations. Let
![]() $\mathscr{P}^{0}$
be the Picard stack of
$\mathscr{P}^{0}$
be the Picard stack of
![]() $J^{0}$
-torsors on
$J^{0}$
-torsors on
![]() $C$
, and let
$C$
, and let
![]() $P^{0}$
(respectively
$P^{0}$
(respectively
![]() $P^{1}$
) be the neutral connected components of the coarse moduli space of
$P^{1}$
) be the neutral connected components of the coarse moduli space of
![]() $\mathscr{P}^{0}$
(respectively
$\mathscr{P}^{0}$
(respectively
![]() $\mathscr{P}^{1}$
).
$\mathscr{P}^{1}$
).
We first understand
![]() $P^{1}$
. Let
$P^{1}$
. Let
![]() $\operatorname{Jac}$
denote the Jacobi variety of
$\operatorname{Jac}$
denote the Jacobi variety of
![]() $\widetilde{C}$
. Then
$\widetilde{C}$
. Then
 $\operatorname{Jac}\otimes \mathbb{X}_{\bullet }$
is the neutral connected component of the coarse moduli space of
$\operatorname{Jac}\otimes \mathbb{X}_{\bullet }$
is the neutral connected component of the coarse moduli space of
![]() $\operatorname{Bun}_{T}$
.
$\operatorname{Bun}_{T}$
.
Lemma 3.5.1. The map
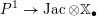 $P^{1}\rightarrow \operatorname{Jac}\otimes \mathbb{X}_{\bullet }$
is an embedding, and
$P^{1}\rightarrow \operatorname{Jac}\otimes \mathbb{X}_{\bullet }$
is an embedding, and
![]() $P^{1}$
can be identified with
$P^{1}$
can be identified with
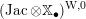 $(\operatorname{Jac}\otimes \mathbb{X}_{\bullet })^{\text{W},0}$
, the neutral connected component of the
$(\operatorname{Jac}\otimes \mathbb{X}_{\bullet })^{\text{W},0}$
, the neutral connected component of the
![]() $\text{W}$
-fixed point subscheme of
$\text{W}$
-fixed point subscheme of
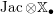 $\operatorname{Jac}\otimes \mathbb{X}_{\bullet }$
.
$\operatorname{Jac}\otimes \mathbb{X}_{\bullet }$
.
Proof. We first show that
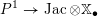 $P^{1}\rightarrow \operatorname{Jac}\otimes \mathbb{X}_{\bullet }$
is injective at the level of
$P^{1}\rightarrow \operatorname{Jac}\otimes \mathbb{X}_{\bullet }$
is injective at the level of
![]() $k$
-points. Indeed, up to isomorphism, the strongly
$k$
-points. Indeed, up to isomorphism, the strongly
![]() $\text{W}$
-equivariant structures on a trivializable
$\text{W}$
-equivariant structures on a trivializable
![]() $T$
-torsor on
$T$
-torsor on
![]() $\widetilde{C}$
are classified by
$\widetilde{C}$
are classified by
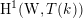 $\operatorname{H}^{1}(\text{W},T(k))$
. By Lemma 3.1.2, the kernel of
$\operatorname{H}^{1}(\text{W},T(k))$
. By Lemma 3.1.2, the kernel of
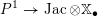 $P^{1}\rightarrow \operatorname{Jac}\otimes \mathbb{X}_{\bullet }$
can be identified with the kernel of the natural map
$P^{1}\rightarrow \operatorname{Jac}\otimes \mathbb{X}_{\bullet }$
can be identified with the kernel of the natural map
 $$\begin{eqnarray}\operatorname{H}^{1}(\text{W},T(k))\rightarrow \bigoplus _{\widetilde{C}_{\unicode[STIX]{x1D6FC}}}T_{\unicode[STIX]{x1D6FC}}(\widetilde{C}_{\unicode[STIX]{x1D6FC}}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{H}^{1}(\text{W},T(k))\rightarrow \bigoplus _{\widetilde{C}_{\unicode[STIX]{x1D6FC}}}T_{\unicode[STIX]{x1D6FC}}(\widetilde{C}_{\unicode[STIX]{x1D6FC}}).\end{eqnarray}$$
Therefore, it is enough to show that this latter map is injective. Over
![]() $B^{0}$
,
$B^{0}$
,
![]() $\widetilde{C}_{\unicode[STIX]{x1D6FC}}$
is non-empty for every root
$\widetilde{C}_{\unicode[STIX]{x1D6FC}}$
is non-empty for every root
![]() $\unicode[STIX]{x1D6FC}$
.Footnote
3
Then the injectivity is a consequence of the following lemma applied to
$\unicode[STIX]{x1D6FC}$
.Footnote
3
Then the injectivity is a consequence of the following lemma applied to
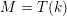 $M=T(k)$
.
$M=T(k)$
.
Lemma 3.5.2. Let
![]() $M$
be a
$M$
be a
![]() $\text{W}$
-module satisfying the following condition: for some (and therefore any) choice of a set of simple roots
$\text{W}$
-module satisfying the following condition: for some (and therefore any) choice of a set of simple roots
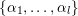 $\{\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{l}\}$
, the natural map
$\{\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{l}\}$
, the natural map
 $$\begin{eqnarray}M\rightarrow \mathop{\prod }_{i=1}^{l}(1-s_{\unicode[STIX]{x1D6FC}_{i}})M,\quad m\mapsto ((1-s_{\unicode[STIX]{x1D6FC}_{1}})m,\ldots ,(1-s_{\unicode[STIX]{x1D6FC}_{l}})m)\end{eqnarray}$$
$$\begin{eqnarray}M\rightarrow \mathop{\prod }_{i=1}^{l}(1-s_{\unicode[STIX]{x1D6FC}_{i}})M,\quad m\mapsto ((1-s_{\unicode[STIX]{x1D6FC}_{1}})m,\ldots ,(1-s_{\unicode[STIX]{x1D6FC}_{l}})m)\end{eqnarray}$$
is surjective. Then the natural map
 $$\begin{eqnarray}\text{H}^{1}(W,M)\rightarrow \mathop{\prod }_{1\leqslant i\leqslant s}M/(1-s_{\unicode[STIX]{x1D6FD}_{i}})M,\quad [c]\mapsto \mathop{\prod }_{1\leqslant i\leqslant s}(c(s_{\unicode[STIX]{x1D6FD}_{i}})~\text{mod}~(1-s_{\unicode[STIX]{x1D6FD}_{i}})M)\end{eqnarray}$$
$$\begin{eqnarray}\text{H}^{1}(W,M)\rightarrow \mathop{\prod }_{1\leqslant i\leqslant s}M/(1-s_{\unicode[STIX]{x1D6FD}_{i}})M,\quad [c]\mapsto \mathop{\prod }_{1\leqslant i\leqslant s}(c(s_{\unicode[STIX]{x1D6FD}_{i}})~\text{mod}~(1-s_{\unicode[STIX]{x1D6FD}_{i}})M)\end{eqnarray}$$
is injective for any choice of a set
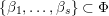 $\{\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{s}\}\subset \unicode[STIX]{x1D6F7}$
of representatives of
$\{\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{s}\}\subset \unicode[STIX]{x1D6F7}$
of representatives of
![]() $\unicode[STIX]{x1D6F7}/\text{W}$
.
$\unicode[STIX]{x1D6F7}/\text{W}$
.
Proof. Let
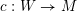 $c:W\rightarrow M$
be a cocycle. It follows from the cocycle condition that if
$c:W\rightarrow M$
be a cocycle. It follows from the cocycle condition that if
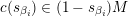 $c(s_{\unicode[STIX]{x1D6FD}_{i}})\in (1-s_{\unicode[STIX]{x1D6FD}_{i}})M$
, then
$c(s_{\unicode[STIX]{x1D6FD}_{i}})\in (1-s_{\unicode[STIX]{x1D6FD}_{i}})M$
, then
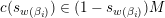 $c(s_{w(\unicode[STIX]{x1D6FD}_{i})})\in (1-s_{w(\unicode[STIX]{x1D6FD}_{i})})M$
. Therefore, a class
$c(s_{w(\unicode[STIX]{x1D6FD}_{i})})\in (1-s_{w(\unicode[STIX]{x1D6FD}_{i})})M$
. Therefore, a class
![]() $[c]$
is in the kernel of the map in the lemma only if
$[c]$
is in the kernel of the map in the lemma only if
 $c(s_{\unicode[STIX]{x1D6FC}_{i}})\in (1-s_{\unicode[STIX]{x1D6FC}_{i}})M$
for a set of simple roots
$c(s_{\unicode[STIX]{x1D6FC}_{i}})\in (1-s_{\unicode[STIX]{x1D6FC}_{i}})M$
for a set of simple roots
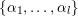 $\{\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{l}\}$
. However, by our assumption of
$\{\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{l}\}$
. However, by our assumption of
![]() $M$
, there exists
$M$
, there exists
![]() $m\in M$
such that
$m\in M$
such that
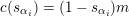 $c(s_{\unicode[STIX]{x1D6FC}_{i}})=(1-s_{\unicode[STIX]{x1D6FC}_{i}})m$
for all
$c(s_{\unicode[STIX]{x1D6FC}_{i}})=(1-s_{\unicode[STIX]{x1D6FC}_{i}})m$
for all
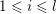 $1\leqslant i\leqslant l$
. Then using the cocycle condition, one can show by induction on the length of
$1\leqslant i\leqslant l$
. Then using the cocycle condition, one can show by induction on the length of
![]() $w$
that
$w$
that
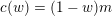 $c(w)=(1-w)m$
for every
$c(w)=(1-w)m$
for every
![]() $w\in \text{W}$
. This means, however, that
$w\in \text{W}$
. This means, however, that
![]() $c$
is a coboundary.◻
$c$
is a coboundary.◻
To complete the proof, observe that the restriction of the norm map
 $$\begin{eqnarray}\operatorname{Nm}:\operatorname{Jac}\otimes \mathbb{X}_{\bullet }\rightarrow P\rightarrow P^{1}\rightarrow (\operatorname{Jac}\otimes \mathbb{X}_{\bullet })^{\text{W}}\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Nm}:\operatorname{Jac}\otimes \mathbb{X}_{\bullet }\rightarrow P\rightarrow P^{1}\rightarrow (\operatorname{Jac}\otimes \mathbb{X}_{\bullet })^{\text{W}}\end{eqnarray}$$
to
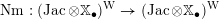 $\operatorname{Nm}:(\operatorname{Jac}\otimes \mathbb{X}_{\bullet })^{\text{W}}\rightarrow (\operatorname{Jac}\otimes \mathbb{X}_{\bullet })^{\text{W}}$
is the multiplication by
$\operatorname{Nm}:(\operatorname{Jac}\otimes \mathbb{X}_{\bullet })^{\text{W}}\rightarrow (\operatorname{Jac}\otimes \mathbb{X}_{\bullet })^{\text{W}}$
is the multiplication by
![]() $|\text{W}|$
. Therefore, the image of
$|\text{W}|$
. Therefore, the image of
 $P^{1}\rightarrow \operatorname{Jac}\otimes \mathbb{X}_{\bullet }$
is
$P^{1}\rightarrow \operatorname{Jac}\otimes \mathbb{X}_{\bullet }$
is
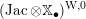 $(\operatorname{Jac}\otimes \mathbb{X}_{\bullet })^{\text{W},0}$
. In addition,
$(\operatorname{Jac}\otimes \mathbb{X}_{\bullet })^{\text{W},0}$
. In addition,
 $P^{1}\rightarrow (\operatorname{Jac}\otimes \mathbb{X}_{\bullet })^{\text{W},0}$
is a prime-to-
$P^{1}\rightarrow (\operatorname{Jac}\otimes \mathbb{X}_{\bullet })^{\text{W},0}$
is a prime-to-
![]() $p$
isogeny and therefore its kernel is étale. Then this kernel must be trivial since its underlying group of
$p$
isogeny and therefore its kernel is étale. Then this kernel must be trivial since its underlying group of
![]() $k$
-points is trivial.◻
$k$
-points is trivial.◻
As a result, for any prime
![]() $\ell \neq p$
,
$\ell \neq p$
,
 $$\begin{eqnarray}T_{\ell }P^{1}\simeq (\text{H}^{1}(\widetilde{C},\mathbb{Z}_{\ell }(1))\otimes \mathbb{X}_{\bullet })^{\text{W}}.\end{eqnarray}$$
$$\begin{eqnarray}T_{\ell }P^{1}\simeq (\text{H}^{1}(\widetilde{C},\mathbb{Z}_{\ell }(1))\otimes \mathbb{X}_{\bullet })^{\text{W}}.\end{eqnarray}$$
In addition, observe that from the definition of
![]() $D_{\text{cl}}$
, the map
$D_{\text{cl}}$
, the map
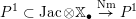 $P^{1}\subset \operatorname{Jac}\otimes \mathbb{X}_{\bullet }\stackrel{\operatorname{Nm}}{\rightarrow }P^{1}$
factors as
$P^{1}\subset \operatorname{Jac}\otimes \mathbb{X}_{\bullet }\stackrel{\operatorname{Nm}}{\rightarrow }P^{1}$
factors as
 $$\begin{eqnarray}P^{1}\subset \operatorname{Jac}\otimes \mathbb{X}_{\bullet }\simeq (\operatorname{Jac}\otimes \mathbb{X}^{\bullet })^{\vee }\rightarrow (\breve{P}^{1})^{\vee }\rightarrow \breve{P}^{\vee }\stackrel{\breve{D}_{\text{cl}}}{\rightarrow }P\rightarrow P^{1}.\end{eqnarray}$$
$$\begin{eqnarray}P^{1}\subset \operatorname{Jac}\otimes \mathbb{X}_{\bullet }\simeq (\operatorname{Jac}\otimes \mathbb{X}^{\bullet })^{\vee }\rightarrow (\breve{P}^{1})^{\vee }\rightarrow \breve{P}^{\vee }\stackrel{\breve{D}_{\text{cl}}}{\rightarrow }P\rightarrow P^{1}.\end{eqnarray}$$
Therefore
![]() $D_{\text{cl}}$
is a prime-to-
$D_{\text{cl}}$
is a prime-to-
![]() $p$
isogeny. In addition, the map
$p$
isogeny. In addition, the map
 $$\begin{eqnarray}T_{\ell }\operatorname{Nm}:T_{\ell }(\operatorname{Jac}\otimes \mathbb{X}_{\bullet }){\twoheadrightarrow}T_{\ell }(\breve{P}^{1})^{\vee }{\hookrightarrow}T_{\ell }P^{1}\end{eqnarray}$$
$$\begin{eqnarray}T_{\ell }\operatorname{Nm}:T_{\ell }(\operatorname{Jac}\otimes \mathbb{X}_{\bullet }){\twoheadrightarrow}T_{\ell }(\breve{P}^{1})^{\vee }{\hookrightarrow}T_{\ell }P^{1}\end{eqnarray}$$
can be identified with
 $$\begin{eqnarray}\operatorname{Nm}:\text{H}^{1}(\widetilde{C},\mathbb{Z}_{\ell }(1))\otimes \mathbb{X}_{\bullet }{\twoheadrightarrow}(\text{H}^{1}(\widetilde{C},\mathbb{Z}_{\ell }(1))\otimes \mathbb{X}_{\bullet })_{\text{W}}/(\operatorname{torsion}){\hookrightarrow}(\text{H}^{1}(\widetilde{C},\mathbb{Z}_{\ell }(1))\otimes \mathbb{X}_{\bullet })^{\text{W}}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Nm}:\text{H}^{1}(\widetilde{C},\mathbb{Z}_{\ell }(1))\otimes \mathbb{X}_{\bullet }{\twoheadrightarrow}(\text{H}^{1}(\widetilde{C},\mathbb{Z}_{\ell }(1))\otimes \mathbb{X}_{\bullet })_{\text{W}}/(\operatorname{torsion}){\hookrightarrow}(\text{H}^{1}(\widetilde{C},\mathbb{Z}_{\ell }(1))\otimes \mathbb{X}_{\bullet })^{\text{W}}.\end{eqnarray}$$
On the other hand, as
![]() $J^{0}$
is connected, the norm map
$J^{0}$
is connected, the norm map
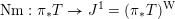 $\operatorname{Nm}:\unicode[STIX]{x1D70B}_{\ast }T\rightarrow J^{1}=(\unicode[STIX]{x1D70B}_{\ast }T)^{\text{W}}$
factors as
$\operatorname{Nm}:\unicode[STIX]{x1D70B}_{\ast }T\rightarrow J^{1}=(\unicode[STIX]{x1D70B}_{\ast }T)^{\text{W}}$
factors as
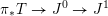 $\unicode[STIX]{x1D70B}_{\ast }T\rightarrow J^{0}\rightarrow J^{1}$
. Therefore,
$\unicode[STIX]{x1D70B}_{\ast }T\rightarrow J^{0}\rightarrow J^{1}$
. Therefore,
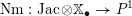 $\operatorname{Nm}:\operatorname{Jac}\otimes \mathbb{X}_{\bullet }\rightarrow P^{1}$
also factors as
$\operatorname{Nm}:\operatorname{Jac}\otimes \mathbb{X}_{\bullet }\rightarrow P^{1}$
also factors as
 $$\begin{eqnarray}\operatorname{Nm}:\operatorname{Jac}\otimes \mathbb{X}_{\bullet }\rightarrow P^{0}\rightarrow P^{1}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Nm}:\operatorname{Jac}\otimes \mathbb{X}_{\bullet }\rightarrow P^{0}\rightarrow P^{1}.\end{eqnarray}$$
It follows that
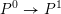 $P^{0}\rightarrow P^{1}$
is also a prime-to-
$P^{0}\rightarrow P^{1}$
is also a prime-to-
![]() $p$
isogeny, and for
$p$
isogeny, and for
![]() $\ell \neq p$
there is a factorization
$\ell \neq p$
there is a factorization
 $$\begin{eqnarray}\operatorname{Nm}:\text{H}^{1}(\widetilde{C},\mathbb{Z}_{\ell }(1))\otimes \mathbb{X}_{\bullet }\rightarrow T_{\ell }P^{0}{\hookrightarrow}(\text{H}^{1}(\widetilde{C},\mathbb{Z}_{\ell }(1))\otimes \mathbb{X}_{\bullet })^{\text{W}}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Nm}:\text{H}^{1}(\widetilde{C},\mathbb{Z}_{\ell }(1))\otimes \mathbb{X}_{\bullet }\rightarrow T_{\ell }P^{0}{\hookrightarrow}(\text{H}^{1}(\widetilde{C},\mathbb{Z}_{\ell }(1))\otimes \mathbb{X}_{\bullet })^{\text{W}}.\end{eqnarray}$$
We need the following key result.
Proposition 3.5.3. The two isogenies
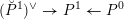 $(\breve{P}^{1})^{\vee }\rightarrow P^{1}\leftarrow P^{0}$
induce an isomorphism
$(\breve{P}^{1})^{\vee }\rightarrow P^{1}\leftarrow P^{0}$
induce an isomorphism
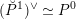 $(\breve{P}^{1})^{\vee }\simeq P^{0}$
.
$(\breve{P}^{1})^{\vee }\simeq P^{0}$
.
Proof. By the above considerations, the lemma is equivalent to saying that the induced map of Tate modules
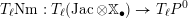 $T_{\ell }\operatorname{Nm}:T_{\ell }(\operatorname{Jac}\otimes \mathbb{X}_{\bullet })\rightarrow T_{\ell }P^{0}$
is surjective for every
$T_{\ell }\operatorname{Nm}:T_{\ell }(\operatorname{Jac}\otimes \mathbb{X}_{\bullet })\rightarrow T_{\ell }P^{0}$
is surjective for every
![]() $\ell \neq p$
.
$\ell \neq p$
.
Note that we have the following commutative diagram

where the left vertical arrow is induced by
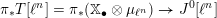 $\unicode[STIX]{x1D70B}_{\ast }T[\ell ^{n}]=\unicode[STIX]{x1D70B}_{\ast }(\mathbb{X}_{\bullet }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}})\rightarrow J^{0}[\ell ^{n}]$
, and the bottom row is induced by the Kummer sequence for
$\unicode[STIX]{x1D70B}_{\ast }T[\ell ^{n}]=\unicode[STIX]{x1D70B}_{\ast }(\mathbb{X}_{\bullet }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}})\rightarrow J^{0}[\ell ^{n}]$
, and the bottom row is induced by the Kummer sequence for
![]() $J^{0}$
and therefore is surjective. Since
$J^{0}$
and therefore is surjective. Since
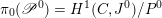 $\unicode[STIX]{x1D70B}_{0}(\mathscr{P}^{0})=H^{1}(C,J^{0})/P^{0}$
is finitely generated, passing to the inverse limit gives
$\unicode[STIX]{x1D70B}_{0}(\mathscr{P}^{0})=H^{1}(C,J^{0})/P^{0}$
is finitely generated, passing to the inverse limit gives

where the bottom arrow is surjective. So it is enough to show that the left vertical arrow is also surjective.
Let
![]() $y\in C$
, and choose a point
$y\in C$
, and choose a point
![]() ${\tilde{y}}\in \widetilde{C}$
lying over
${\tilde{y}}\in \widetilde{C}$
lying over
![]() $y$
. Let
$y$
. Let
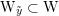 $\text{W}_{{\tilde{y}}}\subset \text{W}$
denote the stabilizer of
$\text{W}_{{\tilde{y}}}\subset \text{W}$
denote the stabilizer of
![]() ${\tilde{y}}$
under the action of
${\tilde{y}}$
under the action of
![]() $\text{W}$
on
$\text{W}$
on
![]() $\widetilde{C}$
. Note that
$\widetilde{C}$
. Note that
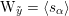 $\text{W}_{{\tilde{y}}}=\langle s_{\unicode[STIX]{x1D6FC}}\rangle$
if
$\text{W}_{{\tilde{y}}}=\langle s_{\unicode[STIX]{x1D6FC}}\rangle$
if
![]() ${\tilde{y}}\in \widetilde{C}_{\unicode[STIX]{x1D6FC}}$
and is trivial otherwise. Then the inclusion of
${\tilde{y}}\in \widetilde{C}_{\unicode[STIX]{x1D6FC}}$
and is trivial otherwise. Then the inclusion of
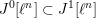 $J^{0}[\ell ^{n}]\subset J^{1}[\ell ^{n}]$
at
$J^{0}[\ell ^{n}]\subset J^{1}[\ell ^{n}]$
at
![]() $y$
can be identified as
$y$
can be identified as
 $$\begin{eqnarray}J^{0}[\ell ^{n}]_{y}\simeq T^{\text{W}_{{\tilde{y}}},0}[\ell ^{n}]=\mathbb{X}_{\bullet }^{\text{W}_{{\tilde{y}}}}\otimes \unicode[STIX]{x1D707}_{\ell ^{n}}\subset J^{1}[\ell ^{n}]_{y}\simeq T^{\text{W}_{{\tilde{y}}}}[\ell ^{n}]=(\mathbb{X}_{\bullet }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}})^{\text{W}_{{\tilde{y}}}}.\end{eqnarray}$$
$$\begin{eqnarray}J^{0}[\ell ^{n}]_{y}\simeq T^{\text{W}_{{\tilde{y}}},0}[\ell ^{n}]=\mathbb{X}_{\bullet }^{\text{W}_{{\tilde{y}}}}\otimes \unicode[STIX]{x1D707}_{\ell ^{n}}\subset J^{1}[\ell ^{n}]_{y}\simeq T^{\text{W}_{{\tilde{y}}}}[\ell ^{n}]=(\mathbb{X}_{\bullet }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}})^{\text{W}_{{\tilde{y}}}}.\end{eqnarray}$$
Therefore, the cokernel of the inclusion
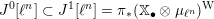 $J^{0}[\ell ^{n}]\subset J^{1}[\ell ^{n}]=\unicode[STIX]{x1D70B}_{\ast }(\mathbb{X}_{\bullet }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}})^{\text{W}}$
is a sheaf supported on the ramification loci of
$J^{0}[\ell ^{n}]\subset J^{1}[\ell ^{n}]=\unicode[STIX]{x1D70B}_{\ast }(\mathbb{X}_{\bullet }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}})^{\text{W}}$
is a sheaf supported on the ramification loci of
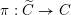 $\unicode[STIX]{x1D70B}:\widetilde{C}\rightarrow C$
, and whose stalk at
$\unicode[STIX]{x1D70B}:\widetilde{C}\rightarrow C$
, and whose stalk at
![]() $y$
can be identified with
$y$
can be identified with
 $\text{H}^{1}(\text{W}_{{\tilde{y}}},\mathbb{X}_{\bullet })[\ell ^{n}]\otimes \unicode[STIX]{x1D707}_{\ell ^{n}}$
. Since
$\text{H}^{1}(\text{W}_{{\tilde{y}}},\mathbb{X}_{\bullet })[\ell ^{n}]\otimes \unicode[STIX]{x1D707}_{\ell ^{n}}$
. Since
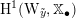 $\text{H}^{1}(\text{W}_{{\tilde{y}}},\mathbb{X}_{\bullet })$
is a finite group, passing to the inverse limit gives
$\text{H}^{1}(\text{W}_{{\tilde{y}}},\mathbb{X}_{\bullet })$
is a finite group, passing to the inverse limit gives
 $$\begin{eqnarray}\mathop{\varprojlim }\nolimits_{n}\operatorname{H}^{1}(C,J^{0}[\ell ^{n}])\simeq \mathop{\varprojlim }\nolimits_{n}\text{H}^{1}(C,\unicode[STIX]{x1D70B}_{\ast }(\mathbb{X}_{\bullet }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}})^{\text{W}}).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\varprojlim }\nolimits_{n}\operatorname{H}^{1}(C,J^{0}[\ell ^{n}])\simeq \mathop{\varprojlim }\nolimits_{n}\text{H}^{1}(C,\unicode[STIX]{x1D70B}_{\ast }(\mathbb{X}_{\bullet }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}})^{\text{W}}).\end{eqnarray}$$
Therefore, it is enough to show that the inverse limit of the system of maps
 $$\begin{eqnarray}\operatorname{Nm}:\text{H}^{1}(C,\unicode[STIX]{x1D70B}_{\ast }(\mathbb{X}_{\bullet }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}}))\rightarrow \text{H}^{1}(C,\unicode[STIX]{x1D70B}_{\ast }(\mathbb{X}_{\bullet }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}})^{\text{W}})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Nm}:\text{H}^{1}(C,\unicode[STIX]{x1D70B}_{\ast }(\mathbb{X}_{\bullet }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}}))\rightarrow \text{H}^{1}(C,\unicode[STIX]{x1D70B}_{\ast }(\mathbb{X}_{\bullet }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}})^{\text{W}})\end{eqnarray}$$
is surjective.
Let
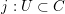 $j:U\subset C$
be the complement of the ramification loci of
$j:U\subset C$
be the complement of the ramification loci of
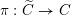 $\unicode[STIX]{x1D70B}:\widetilde{C}\rightarrow C$
and let
$\unicode[STIX]{x1D70B}:\widetilde{C}\rightarrow C$
and let
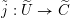 $\tilde{j}:\widetilde{U}\rightarrow \widetilde{C}$
be its preimage in
$\tilde{j}:\widetilde{U}\rightarrow \widetilde{C}$
be its preimage in
![]() $\widetilde{C}$
. Let
$\widetilde{C}$
. Let
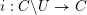 $i:C\setminus U\rightarrow C$
be the closed embedding of ramification loci. Then
$i:C\setminus U\rightarrow C$
be the closed embedding of ramification loci. Then
 $L_{n}:=\unicode[STIX]{x1D70B}_{\ast }(\mathbb{X}_{\bullet }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}})|_{U}$
is a locally free
$L_{n}:=\unicode[STIX]{x1D70B}_{\ast }(\mathbb{X}_{\bullet }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}})|_{U}$
is a locally free
![]() $\mathbb{Z}/\ell ^{n}$
-module on
$\mathbb{Z}/\ell ^{n}$
-module on
![]() $U$
with an action of
$U$
with an action of
![]() $\text{W}$
, and the norm map
$\text{W}$
, and the norm map
 $\operatorname{Nm}:L_{n}\rightarrow L_{n}^{\text{W}}$
is surjective. Let
$\operatorname{Nm}:L_{n}\rightarrow L_{n}^{\text{W}}$
is surjective. Let
![]() $F_{n}$
denote its kernel. Note that since
$F_{n}$
denote its kernel. Note that since
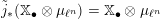 $\tilde{j}_{\ast }(\mathbb{X}_{\bullet }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}})=\mathbb{X}_{\bullet }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}}$
, we have
$\tilde{j}_{\ast }(\mathbb{X}_{\bullet }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}})=\mathbb{X}_{\bullet }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}}$
, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{\ast }(\mathbb{X}_{\bullet }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}})=j_{\ast }L_{n},\quad \unicode[STIX]{x1D70B}_{\ast }(\mathbb{X}_{\bullet }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}})^{\text{W}}=j_{\ast }L_{n}^{\text{W}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{\ast }(\mathbb{X}_{\bullet }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}})=j_{\ast }L_{n},\quad \unicode[STIX]{x1D70B}_{\ast }(\mathbb{X}_{\bullet }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}})^{\text{W}}=j_{\ast }L_{n}^{\text{W}}.\end{eqnarray}$$
Now, let
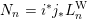 $N_{n}=i^{\ast }j_{\ast }L_{n}^{\text{W}}$
be the restriction of
$N_{n}=i^{\ast }j_{\ast }L_{n}^{\text{W}}$
be the restriction of
![]() $j_{\ast }L_{n}^{\text{W}}$
over the ramification loci. Taking cohomology of
$j_{\ast }L_{n}^{\text{W}}$
over the ramification loci. Taking cohomology of
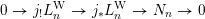 $0\rightarrow j_{!}L_{n}^{\text{W}}\rightarrow j_{\ast }L_{n}^{\text{W}}\rightarrow N_{n}\rightarrow 0$
then induces the following commutative diagram with rows and columns exact.
$0\rightarrow j_{!}L_{n}^{\text{W}}\rightarrow j_{\ast }L_{n}^{\text{W}}\rightarrow N_{n}\rightarrow 0$
then induces the following commutative diagram with rows and columns exact.

Here
![]() $\unicode[STIX]{x1D6E5}_{n}$
and
$\unicode[STIX]{x1D6E5}_{n}$
and
![]() $Q_{n}$
denote the cokernels of the norm maps. Recall that we want to show
$Q_{n}$
denote the cokernels of the norm maps. Recall that we want to show
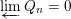 $\varprojlim Q_{n}=0$
. From this diagram, this is equivalent to the surjectivity of
$\varprojlim Q_{n}=0$
. From this diagram, this is equivalent to the surjectivity of
![]() $\mathop{\varprojlim }\nolimits_{n}\unicode[STIX]{x1D6FF}_{n}$
.
$\mathop{\varprojlim }\nolimits_{n}\unicode[STIX]{x1D6FF}_{n}$
.
It is easier to first describe the Pontrjagin dual of
![]() $\unicode[STIX]{x2202}_{n}$
and
$\unicode[STIX]{x2202}_{n}$
and
![]() $q_{n}$
. Note that the distinguished triangle
$q_{n}$
. Note that the distinguished triangle
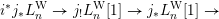 $i^{\ast }j_{\ast }L_{n}^{\text{W}}\rightarrow j_{!}L_{n}^{\text{W}}[1]\rightarrow j_{\ast }L_{n}^{\text{W}}[1]\rightarrow$
is the Verdier dual of the natural distinguished triangle
$i^{\ast }j_{\ast }L_{n}^{\text{W}}\rightarrow j_{!}L_{n}^{\text{W}}[1]\rightarrow j_{\ast }L_{n}^{\text{W}}[1]\rightarrow$
is the Verdier dual of the natural distinguished triangle
 $$\begin{eqnarray}j_{\ast }((L_{n}^{\text{W}})^{\ast }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}})[1]\rightarrow Rj_{\ast }((L_{n}^{\text{W}})^{\ast }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}})[1]\rightarrow R^{1}j_{\ast }((L_{n}^{\text{W}})^{\ast }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}})\rightarrow .\end{eqnarray}$$
$$\begin{eqnarray}j_{\ast }((L_{n}^{\text{W}})^{\ast }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}})[1]\rightarrow Rj_{\ast }((L_{n}^{\text{W}})^{\ast }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}})[1]\rightarrow R^{1}j_{\ast }((L_{n}^{\text{W}})^{\ast }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}})\rightarrow .\end{eqnarray}$$
Therefore, the dual of
![]() $\unicode[STIX]{x2202}_{n}$
is the natural restriction map
$\unicode[STIX]{x2202}_{n}$
is the natural restriction map
 $$\begin{eqnarray}\operatorname{res}:\text{H}^{1}(U,(L_{n}^{\text{W}})^{\ast }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}})\rightarrow \bigoplus _{y\in C-U}\text{H}^{1}(\operatorname{Spec}{\mathcal{O}}_{C,y}^{h}\setminus \{y\},(L_{n}^{\text{W}})^{\ast }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}}),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{res}:\text{H}^{1}(U,(L_{n}^{\text{W}})^{\ast }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}})\rightarrow \bigoplus _{y\in C-U}\text{H}^{1}(\operatorname{Spec}{\mathcal{O}}_{C,y}^{h}\setminus \{y\},(L_{n}^{\text{W}})^{\ast }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}}),\end{eqnarray}$$
where
![]() ${\mathcal{O}}_{C,y}^{h}$
denotes the henselization of
${\mathcal{O}}_{C,y}^{h}$
denotes the henselization of
![]() ${\mathcal{O}}_{C,y}$
.
${\mathcal{O}}_{C,y}$
.
Let
![]() $\bar{\unicode[STIX]{x1D702}}$
denote a geometric generic point of
$\bar{\unicode[STIX]{x1D702}}$
denote a geometric generic point of
![]() $\widetilde{U}$
. Its image in
$\widetilde{U}$
. Its image in
![]() $U$
under
$U$
under
![]() $\unicode[STIX]{x1D70B}$
is still denoted by
$\unicode[STIX]{x1D70B}$
is still denoted by
![]() $\bar{\unicode[STIX]{x1D702}}$
. Then we have
$\bar{\unicode[STIX]{x1D702}}$
. Then we have
 $$\begin{eqnarray}(L_{n})_{\bar{\unicode[STIX]{x1D702}}}\simeq \mathbb{Z}[\text{W}]\otimes (\mathbb{X}_{\bullet }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}}),\end{eqnarray}$$
$$\begin{eqnarray}(L_{n})_{\bar{\unicode[STIX]{x1D702}}}\simeq \mathbb{Z}[\text{W}]\otimes (\mathbb{X}_{\bullet }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}}),\end{eqnarray}$$
and the monodromy representation
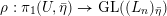 $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(U,\bar{\unicode[STIX]{x1D702}})\rightarrow \operatorname{GL}((L_{n})_{\bar{\unicode[STIX]{x1D702}}})$
is given by
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(U,\bar{\unicode[STIX]{x1D702}})\rightarrow \operatorname{GL}((L_{n})_{\bar{\unicode[STIX]{x1D702}}})$
is given by
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})(a\otimes b)=\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})a\otimes b.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})(a\otimes b)=\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})a\otimes b.\end{eqnarray}$$
There is another action of
![]() $\text{W}$
on
$\text{W}$
on
![]() $(L_{n})_{\bar{\unicode[STIX]{x1D702}}}$
given by
$(L_{n})_{\bar{\unicode[STIX]{x1D702}}}$
given by
 $$\begin{eqnarray}w(a\otimes b)=aw^{-1}\otimes wb,\end{eqnarray}$$
$$\begin{eqnarray}w(a\otimes b)=aw^{-1}\otimes wb,\end{eqnarray}$$
which gives rise to the
![]() $\text{W}$
-action on
$\text{W}$
-action on
![]() $L_{n}$
. Then there is a canonical isomorphism
$L_{n}$
. Then there is a canonical isomorphism
 $$\begin{eqnarray}\mathbb{X}_{\bullet }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}}\simeq (L_{n}^{\text{W}})_{\bar{\unicode[STIX]{x1D702}}},\quad \unicode[STIX]{x1D706}\mapsto \mathop{\sum }_{w\in \text{W}}w\otimes w^{-1}\unicode[STIX]{x1D706}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{X}_{\bullet }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}}\simeq (L_{n}^{\text{W}})_{\bar{\unicode[STIX]{x1D702}}},\quad \unicode[STIX]{x1D706}\mapsto \mathop{\sum }_{w\in \text{W}}w\otimes w^{-1}\unicode[STIX]{x1D706}.\end{eqnarray}$$
Now we have the following commutative diagram

where the second row is the long exact sequence of étale cohomology for locally free
![]() $\mathbb{Z}/\ell ^{n}$
-modules
$\mathbb{Z}/\ell ^{n}$
-modules
 $0\rightarrow (L_{n}^{\text{W}})^{\ast }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}}\rightarrow L_{n}^{\ast }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}}\rightarrow F_{n}^{\ast }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}}\rightarrow 0$
on
$0\rightarrow (L_{n}^{\text{W}})^{\ast }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}}\rightarrow L_{n}^{\ast }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}}\rightarrow F_{n}^{\ast }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}}\rightarrow 0$
on
![]() $U$
, and the first row is the long exact sequence of the group cohomology for their stalks at
$U$
, and the first row is the long exact sequence of the group cohomology for their stalks at
![]() $\bar{\unicode[STIX]{x1D702}}$
, regarded as
$\bar{\unicode[STIX]{x1D702}}$
, regarded as
![]() $\text{W}$
-modules. Here, we use: (i)
$\text{W}$
-modules. Here, we use: (i)
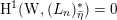 $\text{H}^{1}(\text{W},(L_{n})_{\bar{\unicode[STIX]{x1D702}}}^{\ast })=0$
by Shapiro’s lemma; (ii) under the isomorphism (3.5.3), the
$\text{H}^{1}(\text{W},(L_{n})_{\bar{\unicode[STIX]{x1D702}}}^{\ast })=0$
by Shapiro’s lemma; (ii) under the isomorphism (3.5.3), the
 $\unicode[STIX]{x1D70B}_{1}(U,\bar{\unicode[STIX]{x1D702}})$
-action on
$\unicode[STIX]{x1D70B}_{1}(U,\bar{\unicode[STIX]{x1D702}})$
-action on
![]() $(L_{n}^{\text{W}})_{\bar{\unicode[STIX]{x1D702}}}$
corresponds to the natural action of
$(L_{n}^{\text{W}})_{\bar{\unicode[STIX]{x1D702}}}$
corresponds to the natural action of
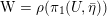 $\text{W}=\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70B}_{1}(U,\bar{\unicode[STIX]{x1D702}}))$
on
$\text{W}=\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70B}_{1}(U,\bar{\unicode[STIX]{x1D702}}))$
on
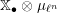 $\mathbb{X}_{\bullet }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}}$
; (iii)
$\mathbb{X}_{\bullet }\otimes \unicode[STIX]{x1D707}_{\ell ^{n}}$
; (iii)
![]() $\unicode[STIX]{x1D70C}^{\ast }$
is injective since it is induced by the surjective map
$\unicode[STIX]{x1D70C}^{\ast }$
is injective since it is induced by the surjective map
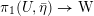 $\unicode[STIX]{x1D70B}_{1}(U,\bar{\unicode[STIX]{x1D702}})\rightarrow \text{W}$
. Therefore, it follows from the Poincaré duality on
$\unicode[STIX]{x1D70B}_{1}(U,\bar{\unicode[STIX]{x1D702}})\rightarrow \text{W}$
. Therefore, it follows from the Poincaré duality on
![]() $U$
that the Pontrjagin dual of
$U$
that the Pontrjagin dual of
![]() $q_{n}$
is
$q_{n}$
is
![]() $\unicode[STIX]{x1D70C}^{\ast }$
.
$\unicode[STIX]{x1D70C}^{\ast }$
.
Putting these considerations together, we see that the dual of
![]() $\unicode[STIX]{x1D6FF}_{n}$
is
$\unicode[STIX]{x1D6FF}_{n}$
is
![]() $\operatorname{res}\circ \unicode[STIX]{x1D70C}^{\ast }$
. Now we choose a geometric generic point
$\operatorname{res}\circ \unicode[STIX]{x1D70C}^{\ast }$
. Now we choose a geometric generic point
![]() $\bar{\unicode[STIX]{x1D702}}_{{\tilde{y}}}$
of
$\bar{\unicode[STIX]{x1D702}}_{{\tilde{y}}}$
of
 $\operatorname{Spec}{\mathcal{O}}_{C,y}^{h}\setminus \{y\}$
over
$\operatorname{Spec}{\mathcal{O}}_{C,y}^{h}\setminus \{y\}$
over
![]() $\bar{\unicode[STIX]{x1D702}}$
. Then
$\bar{\unicode[STIX]{x1D702}}$
. Then
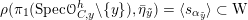 $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70B}_{1}(\operatorname{Spec}{\mathcal{O}}_{C,y}^{h}\setminus \{y\}),\bar{\unicode[STIX]{x1D702}}_{{\tilde{y}}})=\langle s_{\unicode[STIX]{x1D6FC}_{{\tilde{y}}}}\rangle \subset \text{W}$
for some root
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70B}_{1}(\operatorname{Spec}{\mathcal{O}}_{C,y}^{h}\setminus \{y\}),\bar{\unicode[STIX]{x1D702}}_{{\tilde{y}}})=\langle s_{\unicode[STIX]{x1D6FC}_{{\tilde{y}}}}\rangle \subset \text{W}$
for some root
![]() $\unicode[STIX]{x1D6FC}_{{\tilde{y}}}$
(depending on
$\unicode[STIX]{x1D6FC}_{{\tilde{y}}}$
(depending on
![]() $\bar{\unicode[STIX]{x1D702}}_{{\tilde{y}}}$
), and there is the following commutative diagram
$\bar{\unicode[STIX]{x1D702}}_{{\tilde{y}}}$
), and there is the following commutative diagram

with vertical arrows injective. Therefore, it remains to show that
 $$\begin{eqnarray}\bigoplus _{y\in C-U}\varprojlim \text{H}^{1}(\langle s_{\unicode[STIX]{x1D6FC}_{{\tilde{y}}}}\rangle ,\mathbb{X}^{\bullet }/\ell ^{n})^{\ast }\rightarrow \varprojlim \text{H}^{1}(\text{W},\mathbb{X}^{\bullet }/\ell ^{n})^{\ast }\end{eqnarray}$$
$$\begin{eqnarray}\bigoplus _{y\in C-U}\varprojlim \text{H}^{1}(\langle s_{\unicode[STIX]{x1D6FC}_{{\tilde{y}}}}\rangle ,\mathbb{X}^{\bullet }/\ell ^{n})^{\ast }\rightarrow \varprojlim \text{H}^{1}(\text{W},\mathbb{X}^{\bullet }/\ell ^{n})^{\ast }\end{eqnarray}$$
is surjective. Note
 $$\begin{eqnarray}\mathop{\varprojlim }\nolimits_{n}\text{H}^{1}(\text{W},\mathbb{X}^{\bullet }/\ell ^{n})^{\ast }=\operatorname{Hom}\biggl(\mathop{\varinjlim }\nolimits_{n}\operatorname{H}^{1}\biggl(\text{W},\frac{1}{\ell ^{n}}\mathbb{X}^{\bullet }/\mathbb{X}^{\bullet }\biggr),\mathbb{Q}_{\ell }/\mathbb{Z}_{\ell }\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\varprojlim }\nolimits_{n}\text{H}^{1}(\text{W},\mathbb{X}^{\bullet }/\ell ^{n})^{\ast }=\operatorname{Hom}\biggl(\mathop{\varinjlim }\nolimits_{n}\operatorname{H}^{1}\biggl(\text{W},\frac{1}{\ell ^{n}}\mathbb{X}^{\bullet }/\mathbb{X}^{\bullet }\biggr),\mathbb{Q}_{\ell }/\mathbb{Z}_{\ell }\biggr).\end{eqnarray}$$
Using
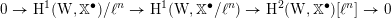 $0\rightarrow \text{H}^{1}(\text{W},\mathbb{X}^{\bullet })/\ell ^{n}\rightarrow \operatorname{H}^{1}(\text{W},\mathbb{X}^{\bullet }/\ell ^{n})\rightarrow \operatorname{H}^{2}(\text{W},\mathbb{X}^{\bullet })[\ell ^{n}]\rightarrow 0$
, and the fact that
$0\rightarrow \text{H}^{1}(\text{W},\mathbb{X}^{\bullet })/\ell ^{n}\rightarrow \operatorname{H}^{1}(\text{W},\mathbb{X}^{\bullet }/\ell ^{n})\rightarrow \operatorname{H}^{2}(\text{W},\mathbb{X}^{\bullet })[\ell ^{n}]\rightarrow 0$
, and the fact that
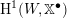 $\operatorname{H}^{1}(W,\mathbb{X}^{\bullet })$
is finite, we have
$\operatorname{H}^{1}(W,\mathbb{X}^{\bullet })$
is finite, we have
 $$\begin{eqnarray}\mathop{\varinjlim }\nolimits_{n}\operatorname{H}^{1}\biggl(\text{W},\frac{1}{\ell ^{n}}\mathbb{X}^{\bullet }/\mathbb{X}^{\bullet }\biggr)=\operatorname{H}^{2}(\text{W},\mathbb{X}^{\bullet })[\ell ^{\infty }]=\operatorname{H}^{1}(\text{W},\mathbb{X}^{\bullet }\otimes \mathbb{Q}_{\ell }/\mathbb{Z}_{\ell }).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\varinjlim }\nolimits_{n}\operatorname{H}^{1}\biggl(\text{W},\frac{1}{\ell ^{n}}\mathbb{X}^{\bullet }/\mathbb{X}^{\bullet }\biggr)=\operatorname{H}^{2}(\text{W},\mathbb{X}^{\bullet })[\ell ^{\infty }]=\operatorname{H}^{1}(\text{W},\mathbb{X}^{\bullet }\otimes \mathbb{Q}_{\ell }/\mathbb{Z}_{\ell }).\end{eqnarray}$$
So it reduces to show that
 $$\begin{eqnarray}\text{H}^{1}(\text{W},\mathbb{X}^{\bullet }\otimes \mathbb{Q}_{\ell }/\mathbb{Z}_{\ell })\rightarrow \bigoplus _{y\in C-U}\text{H}^{1}(\langle s_{\unicode[STIX]{x1D6FC}_{{\tilde{y}}}}\rangle ,\mathbb{X}^{\bullet }\otimes \mathbb{Q}_{\ell }/\mathbb{Z}_{\ell })\end{eqnarray}$$
$$\begin{eqnarray}\text{H}^{1}(\text{W},\mathbb{X}^{\bullet }\otimes \mathbb{Q}_{\ell }/\mathbb{Z}_{\ell })\rightarrow \bigoplus _{y\in C-U}\text{H}^{1}(\langle s_{\unicode[STIX]{x1D6FC}_{{\tilde{y}}}}\rangle ,\mathbb{X}^{\bullet }\otimes \mathbb{Q}_{\ell }/\mathbb{Z}_{\ell })\end{eqnarray}$$
is injective. As mentioned in the proof of Lemma 3.5.1,
![]() $\widetilde{C}_{\unicode[STIX]{x1D6FC}}$
is non-empty for every
$\widetilde{C}_{\unicode[STIX]{x1D6FC}}$
is non-empty for every
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}$
. Hence
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}$
. Hence
![]() $\{\unicode[STIX]{x1D6FC}_{{\tilde{y}}}\}$
contain a set of representatives of
$\{\unicode[STIX]{x1D6FC}_{{\tilde{y}}}\}$
contain a set of representatives of
![]() $\unicode[STIX]{x1D6F7}/\text{W}$
. Now we can apply Lemma 3.5.2 to
$\unicode[STIX]{x1D6F7}/\text{W}$
. Now we can apply Lemma 3.5.2 to
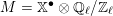 $M=\mathbb{X}^{\bullet }\otimes \mathbb{Q}_{\ell }/\mathbb{Z}_{\ell }$
to finish the proof of the proposition.◻
$M=\mathbb{X}^{\bullet }\otimes \mathbb{Q}_{\ell }/\mathbb{Z}_{\ell }$
to finish the proof of the proposition.◻
Now, let
 $A^{\prime }=\ker (P^{0}\rightarrow P)$
, and
$A^{\prime }=\ker (P^{0}\rightarrow P)$
, and
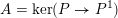 $A=\ker (P\rightarrow P^{1})$
. Then by the above proposition,
$A=\ker (P\rightarrow P^{1})$
. Then by the above proposition,
 $$\begin{eqnarray}\ker D_{\text{cl}}=A^{\prime }/(\breve{A})^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}\ker D_{\text{cl}}=A^{\prime }/(\breve{A})^{\ast }.\end{eqnarray}$$
As both
![]() $A^{\prime }$
and
$A^{\prime }$
and
![]() $\breve{A}$
are finite étale groups, it is enough to show that
$\breve{A}$
are finite étale groups, it is enough to show that
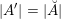 $|A^{\prime }|=|\breve{A}|$
, where for a finite group
$|A^{\prime }|=|\breve{A}|$
, where for a finite group
![]() $\unicode[STIX]{x1D6E4}$
,
$\unicode[STIX]{x1D6E4}$
,
![]() $|\unicode[STIX]{x1D6E4}|$
denotes the number of its elements. This is the subject of the next subsection.
$|\unicode[STIX]{x1D6E4}|$
denotes the number of its elements. This is the subject of the next subsection.
3.6 Calculation of finite groups
Let us understand
![]() $A$
. In fact, it is better to pick up
$A$
. In fact, it is better to pick up
![]() $\infty \in C$
away from the ramification loci. Let
$\infty \in C$
away from the ramification loci. Let
![]() ${\mathcal{O}}_{\infty }$
denote the completed local ring of
${\mathcal{O}}_{\infty }$
denote the completed local ring of
![]() $C$
at
$C$
at
![]() $\infty$
. Let
$\infty$
. Let
![]() $J_{\infty }$
be the dilatation of
$J_{\infty }$
be the dilatation of
![]() $J$
along the unit of the fiber of
$J$
along the unit of the fiber of
![]() $J$
at
$J$
at
![]() $\infty$
. By definition (see [Reference Bosch, Lutkebohmert and RaynaudBLR90, §2] for details),
$\infty$
. By definition (see [Reference Bosch, Lutkebohmert and RaynaudBLR90, §2] for details),
![]() $J_{\infty }$
is the unique smooth group scheme over
$J_{\infty }$
is the unique smooth group scheme over
![]() $C$
equipped with a natural map
$C$
equipped with a natural map
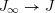 $J_{\infty }\rightarrow J$
, which is an isomorphism away from
$J_{\infty }\rightarrow J$
, which is an isomorphism away from
![]() $\infty$
and induces an isomorphism from
$\infty$
and induces an isomorphism from
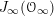 $J_{\infty }({\mathcal{O}}_{\infty })$
to the first congruence subgroup of
$J_{\infty }({\mathcal{O}}_{\infty })$
to the first congruence subgroup of
![]() $J({\mathcal{O}}_{\infty })$
. Let
$J({\mathcal{O}}_{\infty })$
. Let
![]() $\mathscr{P}_{\infty }$
be the Picard stack of
$\mathscr{P}_{\infty }$
be the Picard stack of
![]() $J_{\infty }$
-torsors on
$J_{\infty }$
-torsors on
![]() $C$
. One can also interpret
$C$
. One can also interpret
![]() $\mathscr{P}_{\infty }$
as the Picard stack of
$\mathscr{P}_{\infty }$
as the Picard stack of
![]() $J$
-torsors on
$J$
-torsors on
![]() $C$
together with a trivialization at
$C$
together with a trivialization at
![]() $\infty$
. Observe that
$\infty$
. Observe that
![]() $\mathscr{P}_{\infty }$
is in fact a scheme. Let
$\mathscr{P}_{\infty }$
is in fact a scheme. Let
![]() $P_{\infty }$
denote the neutral connected component of
$P_{\infty }$
denote the neutral connected component of
![]() $\mathscr{P}_{\infty }$
. Similarly, one can define
$\mathscr{P}_{\infty }$
. Similarly, one can define
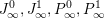 $J_{\infty }^{0},J_{\infty }^{1},P_{\infty }^{0},P_{\infty }^{1}$
etc. Let
$J_{\infty }^{0},J_{\infty }^{1},P_{\infty }^{0},P_{\infty }^{1}$
etc. Let
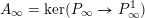 $A_{\infty }=\ker (P_{\infty }\rightarrow P_{\infty }^{1})$
and
$A_{\infty }=\ker (P_{\infty }\rightarrow P_{\infty }^{1})$
and
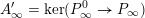 $A_{\infty }^{\prime }=\ker (P_{\infty }^{0}\rightarrow P_{\infty })$
.
$A_{\infty }^{\prime }=\ker (P_{\infty }^{0}\rightarrow P_{\infty })$
.
Lemma 3.6.1. There are the following two exact sequences
 $$\begin{eqnarray}1\rightarrow A_{\infty }\rightarrow \unicode[STIX]{x1D6E4}(C,J^{1}/J)\rightarrow \unicode[STIX]{x1D70B}_{0}(\mathscr{P})\rightarrow \unicode[STIX]{x1D70B}_{0}(\mathscr{P}^{1})\rightarrow 1\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow A_{\infty }\rightarrow \unicode[STIX]{x1D6E4}(C,J^{1}/J)\rightarrow \unicode[STIX]{x1D70B}_{0}(\mathscr{P})\rightarrow \unicode[STIX]{x1D70B}_{0}(\mathscr{P}^{1})\rightarrow 1\end{eqnarray}$$
and
 $$\begin{eqnarray}1\rightarrow \operatorname{Aut}_{\mathscr{P}}(e)\rightarrow \operatorname{Aut}_{\mathscr{P}^{1}}(e)\rightarrow A_{\infty }\rightarrow A\rightarrow 1.\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow \operatorname{Aut}_{\mathscr{P}}(e)\rightarrow \operatorname{Aut}_{\mathscr{P}^{1}}(e)\rightarrow A_{\infty }\rightarrow A\rightarrow 1.\end{eqnarray}$$
Similarly,
 $$\begin{eqnarray}1\rightarrow A_{\infty }^{\prime }\rightarrow \unicode[STIX]{x1D6E4}(C,J/J^{0})\rightarrow \unicode[STIX]{x1D70B}_{0}(\mathscr{P}^{0})\rightarrow \unicode[STIX]{x1D70B}_{0}(\mathscr{P})\rightarrow 1\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow A_{\infty }^{\prime }\rightarrow \unicode[STIX]{x1D6E4}(C,J/J^{0})\rightarrow \unicode[STIX]{x1D70B}_{0}(\mathscr{P}^{0})\rightarrow \unicode[STIX]{x1D70B}_{0}(\mathscr{P})\rightarrow 1\end{eqnarray}$$
and
 $$\begin{eqnarray}1\rightarrow \operatorname{Aut}_{\mathscr{P}^{0}}(e)\rightarrow \operatorname{Aut}_{\mathscr{P}}(e)\rightarrow A_{\infty }^{\prime }\rightarrow A^{\prime }\rightarrow 1.\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow \operatorname{Aut}_{\mathscr{P}^{0}}(e)\rightarrow \operatorname{Aut}_{\mathscr{P}}(e)\rightarrow A_{\infty }^{\prime }\rightarrow A^{\prime }\rightarrow 1.\end{eqnarray}$$
Proof. Consider the following commutative diagram.

Taking
 $R\unicode[STIX]{x1D6E4}(C,-)$
, we obtain the following.
$R\unicode[STIX]{x1D6E4}(C,-)$
, we obtain the following.

Since
![]() $\mathscr{P}_{\infty }$
and
$\mathscr{P}_{\infty }$
and
![]() $\mathscr{P}_{\infty }^{1}$
are schemes, the first row of (3.7.1) gives
$\mathscr{P}_{\infty }^{1}$
are schemes, the first row of (3.7.1) gives
 $$\begin{eqnarray}1\rightarrow A_{\infty }\rightarrow \unicode[STIX]{x1D6E4}(C,J_{\infty }^{1}/J_{\infty })\rightarrow \unicode[STIX]{x1D70B}_{0}(\mathscr{P}_{\infty })\rightarrow \unicode[STIX]{x1D70B}_{0}(\mathscr{P}_{\infty }^{1})\rightarrow 1.\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow A_{\infty }\rightarrow \unicode[STIX]{x1D6E4}(C,J_{\infty }^{1}/J_{\infty })\rightarrow \unicode[STIX]{x1D70B}_{0}(\mathscr{P}_{\infty })\rightarrow \unicode[STIX]{x1D70B}_{0}(\mathscr{P}_{\infty }^{1})\rightarrow 1.\end{eqnarray}$$
Since
 $J_{\infty }^{1}/J_{\infty }=J^{1}/J$
and
$J_{\infty }^{1}/J_{\infty }=J^{1}/J$
and
 $\unicode[STIX]{x1D70B}_{0}(\mathscr{P}_{\infty })=\unicode[STIX]{x1D70B}_{0}(\mathscr{P}),\unicode[STIX]{x1D70B}_{0}(\mathscr{P}_{\infty }^{1})=\unicode[STIX]{x1D70B}_{0}(\mathscr{P}^{1})$
, we obtain the first exact sequence of the lemma. In addition, combining with the second row of (3.7.1), we obtain the short exact sequence of Beilinson
$\unicode[STIX]{x1D70B}_{0}(\mathscr{P}_{\infty })=\unicode[STIX]{x1D70B}_{0}(\mathscr{P}),\unicode[STIX]{x1D70B}_{0}(\mathscr{P}_{\infty }^{1})=\unicode[STIX]{x1D70B}_{0}(\mathscr{P}^{1})$
, we obtain the first exact sequence of the lemma. In addition, combining with the second row of (3.7.1), we obtain the short exact sequence of Beilinson
![]() $1$
-motives
$1$
-motives
 $$\begin{eqnarray}1\rightarrow A_{\infty }\rightarrow W_{1}\mathscr{P}\rightarrow W_{1}\mathscr{P}^{1}\rightarrow 1,\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow A_{\infty }\rightarrow W_{1}\mathscr{P}\rightarrow W_{1}\mathscr{P}^{1}\rightarrow 1,\end{eqnarray}$$
which in turn gives the second exact sequence of the lemma. The proof of the last two exact sequences of the lemma is similar (by considering
![]() $R\unicode[STIX]{x1D6E4}$
of the short exact sequence
$R\unicode[STIX]{x1D6E4}$
of the short exact sequence
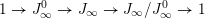 $1\rightarrow J_{\infty }^{0}\rightarrow J_{\infty }\rightarrow J_{\infty }/J_{\infty }^{0}\rightarrow 1$
).◻
$1\rightarrow J_{\infty }^{0}\rightarrow J_{\infty }\rightarrow J_{\infty }/J_{\infty }^{0}\rightarrow 1$
).◻
As a corollary, we can write
 $$\begin{eqnarray}|A|=\frac{|\unicode[STIX]{x1D6E4}(C,J^{1}/J)|}{|\!\operatorname{coker}(\operatorname{Aut}_{\mathscr{P}}(e)\rightarrow \operatorname{Aut}_{\mathscr{P}^{1}}(e))||\!\ker \!(\unicode[STIX]{x1D70B}_{0}(\mathscr{P})\rightarrow \unicode[STIX]{x1D70B}_{0}(\mathscr{P}^{1})|},\end{eqnarray}$$
$$\begin{eqnarray}|A|=\frac{|\unicode[STIX]{x1D6E4}(C,J^{1}/J)|}{|\!\operatorname{coker}(\operatorname{Aut}_{\mathscr{P}}(e)\rightarrow \operatorname{Aut}_{\mathscr{P}^{1}}(e))||\!\ker \!(\unicode[STIX]{x1D70B}_{0}(\mathscr{P})\rightarrow \unicode[STIX]{x1D70B}_{0}(\mathscr{P}^{1})|},\end{eqnarray}$$
and
 $$\begin{eqnarray}|A^{\prime }|=\frac{|\unicode[STIX]{x1D6E4}(C,J/J^{0})|}{|\!\operatorname{coker}(\operatorname{Aut}_{\mathscr{P}^{0}}(e)\rightarrow \operatorname{Aut}_{\mathscr{P}}(e))||\!\ker (\unicode[STIX]{x1D70B}_{0}(\mathscr{P}^{0})\rightarrow \unicode[STIX]{x1D70B}_{0}(\mathscr{P}))|}.\end{eqnarray}$$
$$\begin{eqnarray}|A^{\prime }|=\frac{|\unicode[STIX]{x1D6E4}(C,J/J^{0})|}{|\!\operatorname{coker}(\operatorname{Aut}_{\mathscr{P}^{0}}(e)\rightarrow \operatorname{Aut}_{\mathscr{P}}(e))||\!\ker (\unicode[STIX]{x1D70B}_{0}(\mathscr{P}^{0})\rightarrow \unicode[STIX]{x1D70B}_{0}(\mathscr{P}))|}.\end{eqnarray}$$
Therefore to show that
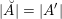 $|\breve{A}|=|A^{\prime }|$
, it is enough to show that:
$|\breve{A}|=|A^{\prime }|$
, it is enough to show that:
-
(1)
 $|\unicode[STIX]{x1D6E4}(C,\breve{J}^{1}/\breve{J})|=|\unicode[STIX]{x1D6E4}(C,J/J^{0})|$
;
$|\unicode[STIX]{x1D6E4}(C,\breve{J}^{1}/\breve{J})|=|\unicode[STIX]{x1D6E4}(C,J/J^{0})|$
; -
(2)
 $|\!\operatorname{coker}(\operatorname{Aut}_{\breve{\mathscr{P}}}(e)\rightarrow \operatorname{Aut}_{\breve{\mathscr{P}}^{1}}(e))|=|\!\operatorname{coker}(\unicode[STIX]{x1D70B}_{0}(\mathscr{P})^{\ast }\rightarrow \unicode[STIX]{x1D70B}_{0}(\mathscr{P}^{0})^{\ast })|$
;
$|\!\operatorname{coker}(\operatorname{Aut}_{\breve{\mathscr{P}}}(e)\rightarrow \operatorname{Aut}_{\breve{\mathscr{P}}^{1}}(e))|=|\!\operatorname{coker}(\unicode[STIX]{x1D70B}_{0}(\mathscr{P})^{\ast }\rightarrow \unicode[STIX]{x1D70B}_{0}(\mathscr{P}^{0})^{\ast })|$
; -
(3)
 $|\!\ker (\unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}})\rightarrow \unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}}^{1}))|=|\!\ker (\operatorname{Aut}_{\mathscr{P}}(e)^{\ast }\rightarrow \operatorname{Aut}_{\mathscr{P}^{0}}(e)^{\ast })|$
.
$|\!\ker (\unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}})\rightarrow \unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}}^{1}))|=|\!\ker (\operatorname{Aut}_{\mathscr{P}}(e)^{\ast }\rightarrow \operatorname{Aut}_{\mathscr{P}^{0}}(e)^{\ast })|$
.
We first prove (1). By (3.1.3),
 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}(C,\breve{J}^{1}/\breve{J})=\biggl(\bigoplus _{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FC}}(\widetilde{C}_{\unicode[STIX]{x1D6FC}})\biggr)^{\text{W}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}(C,\breve{J}^{1}/\breve{J})=\biggl(\bigoplus _{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FC}}(\widetilde{C}_{\unicode[STIX]{x1D6FC}})\biggr)^{\text{W}}.\end{eqnarray}$$
Observe that
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FC}}\neq 0$
if and only if
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FC}}\neq 0$
if and only if
![]() $\unicode[STIX]{x1D6FC}$
is not a primitive root, i.e.,
$\unicode[STIX]{x1D6FC}$
is not a primitive root, i.e.,
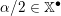 $\unicode[STIX]{x1D6FC}/2\in \mathbb{X}^{\bullet }$
. On the other hand, from
$\unicode[STIX]{x1D6FC}/2\in \mathbb{X}^{\bullet }$
. On the other hand, from
 $$\begin{eqnarray}1\rightarrow J/J_{0}\rightarrow J_{1}/J_{0}\rightarrow J_{1}/J\rightarrow 1,\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow J/J_{0}\rightarrow J_{1}/J_{0}\rightarrow J_{1}/J\rightarrow 1,\end{eqnarray}$$
one can see that the character group of
 $\unicode[STIX]{x1D6E4}(C,J/J_{0})$
is
$\unicode[STIX]{x1D6E4}(C,J/J_{0})$
is
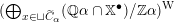 $(\bigoplus _{x\in \sqcup \widetilde{C}_{\unicode[STIX]{x1D6FC}}}(\mathbb{Q}\unicode[STIX]{x1D6FC}\cap \mathbb{X}^{\bullet })/\mathbb{Z}\unicode[STIX]{x1D6FC})^{\text{W}}$
. Then (1) follows.
$(\bigoplus _{x\in \sqcup \widetilde{C}_{\unicode[STIX]{x1D6FC}}}(\mathbb{Q}\unicode[STIX]{x1D6FC}\cap \mathbb{X}^{\bullet })/\mathbb{Z}\unicode[STIX]{x1D6FC})^{\text{W}}$
. Then (1) follows.
Next, we prove (2). In fact, it follows from §3.4 and [Reference NgôNgô10, §4.10] that both maps can be identified with the natural inclusion
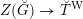 $Z(\breve{G})\rightarrow \breve{T}^{\text{W}}$
.
$Z(\breve{G})\rightarrow \breve{T}^{\text{W}}$
.
Finally, we show (3). Recall that
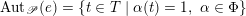 $\operatorname{Aut}_{\mathscr{P}}(e)=\{t\in T\mid \unicode[STIX]{x1D6FC}(t)=1,~\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}\}$
. On the other hand, from the above description of
$\operatorname{Aut}_{\mathscr{P}}(e)=\{t\in T\mid \unicode[STIX]{x1D6FC}(t)=1,~\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}\}$
. On the other hand, from the above description of
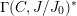 $\unicode[STIX]{x1D6E4}(C,J/J_{0})^{\ast }$
,
$\unicode[STIX]{x1D6E4}(C,J/J_{0})^{\ast }$
,
 $$\begin{eqnarray}\operatorname{Aut}_{\mathscr{P}^{0}}(e)=\{t\in T\mid \unicode[STIX]{x1D706}(t)=1\text{ if }\unicode[STIX]{x1D706}\in \mathbb{Q}\unicode[STIX]{x1D6FC}\cap \mathbb{X}^{\bullet },\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7})\!\}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Aut}_{\mathscr{P}^{0}}(e)=\{t\in T\mid \unicode[STIX]{x1D706}(t)=1\text{ if }\unicode[STIX]{x1D706}\in \mathbb{Q}\unicode[STIX]{x1D6FC}\cap \mathbb{X}^{\bullet },\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7})\!\}.\end{eqnarray}$$
Therefore,
 $$\begin{eqnarray}\ker (\operatorname{Aut}_{\mathscr{P}}(e)^{\ast }\rightarrow \operatorname{Aut}_{\mathscr{ P}^{0}}(e)^{\ast })=\frac{\mathop{\sum }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}}(\mathbb{Q}\unicode[STIX]{x1D6FC}\cap \mathbb{X}^{\bullet })}{\mathbb{Z}\unicode[STIX]{x1D6F7}}.\end{eqnarray}$$
$$\begin{eqnarray}\ker (\operatorname{Aut}_{\mathscr{P}}(e)^{\ast }\rightarrow \operatorname{Aut}_{\mathscr{ P}^{0}}(e)^{\ast })=\frac{\mathop{\sum }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}}(\mathbb{Q}\unicode[STIX]{x1D6FC}\cap \mathbb{X}^{\bullet })}{\mathbb{Z}\unicode[STIX]{x1D6F7}}.\end{eqnarray}$$
To calculate
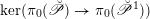 $\ker (\unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}})\rightarrow \unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}}^{1}))$
, we choose
$\ker (\unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}})\rightarrow \unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}}^{1}))$
, we choose
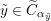 ${\tilde{y}}\in \widetilde{C}_{\unicode[STIX]{x1D6FC}_{{\tilde{y}}}}$
above
${\tilde{y}}\in \widetilde{C}_{\unicode[STIX]{x1D6FC}_{{\tilde{y}}}}$
above
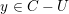 $y\in C-U$
for every point in the ramification loci. The restriction of
$y\in C-U$
for every point in the ramification loci. The restriction of
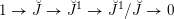 $1\rightarrow \breve{J}\rightarrow \breve{J}^{1}\rightarrow \breve{J}^{1}/\breve{J}\rightarrow 0$
at
$1\rightarrow \breve{J}\rightarrow \breve{J}^{1}\rightarrow \breve{J}^{1}/\breve{J}\rightarrow 0$
at
![]() $y$
then can be identified with
$y$
then can be identified with
 $$\begin{eqnarray}1\rightarrow \ker (\breve{\unicode[STIX]{x1D6FC}}_{{\tilde{y}}})\rightarrow \breve{T}^{s_{\unicode[STIX]{x1D6FC}_{{\tilde{y}}}}}\stackrel{\breve{\unicode[STIX]{x1D6FC}}_{{\tilde{y}}}}{\rightarrow }\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FC}_{{\tilde{y}}}}\simeq \frac{\mathbb{Q}\unicode[STIX]{x1D6FC}_{{\tilde{y}}}\cap \mathbb{X}^{\bullet }}{\mathbb{Z}\unicode[STIX]{x1D6FC}_{{\tilde{y}}}}\rightarrow 1.\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow \ker (\breve{\unicode[STIX]{x1D6FC}}_{{\tilde{y}}})\rightarrow \breve{T}^{s_{\unicode[STIX]{x1D6FC}_{{\tilde{y}}}}}\stackrel{\breve{\unicode[STIX]{x1D6FC}}_{{\tilde{y}}}}{\rightarrow }\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FC}_{{\tilde{y}}}}\simeq \frac{\mathbb{Q}\unicode[STIX]{x1D6FC}_{{\tilde{y}}}\cap \mathbb{X}^{\bullet }}{\mathbb{Z}\unicode[STIX]{x1D6FC}_{{\tilde{y}}}}\rightarrow 1.\end{eqnarray}$$
It follows that the coboundary map
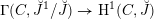 $\unicode[STIX]{x1D6E4}(C,\breve{J}^{1}/\breve{J})\rightarrow \text{H}^{1}(C,\breve{J})$
can be identified with
$\unicode[STIX]{x1D6E4}(C,\breve{J}^{1}/\breve{J})\rightarrow \text{H}^{1}(C,\breve{J})$
can be identified with
 $$\begin{eqnarray}\bigoplus _{y\in C-U}\frac{\mathbb{Q}\unicode[STIX]{x1D6FC}_{{\tilde{y}}}\cap \mathbb{X}^{\bullet }}{\mathbb{Z}\unicode[STIX]{x1D6FC}_{{\tilde{y}}}}\rightarrow \text{H}^{1}(C,\breve{J}),\quad \unicode[STIX]{x1D706}_{{\tilde{y}}}\in \frac{\mathbb{Q}\unicode[STIX]{x1D6FC}_{{\tilde{y}}}\cap \mathbb{X}^{\bullet }}{\mathbb{Z}\unicode[STIX]{x1D6FC}_{{\tilde{y}}}}\mapsto \operatorname{AJ}^{\breve{\mathscr{P}}}({\tilde{y}},\unicode[STIX]{x1D706}_{{\tilde{y}}}),\end{eqnarray}$$
$$\begin{eqnarray}\bigoplus _{y\in C-U}\frac{\mathbb{Q}\unicode[STIX]{x1D6FC}_{{\tilde{y}}}\cap \mathbb{X}^{\bullet }}{\mathbb{Z}\unicode[STIX]{x1D6FC}_{{\tilde{y}}}}\rightarrow \text{H}^{1}(C,\breve{J}),\quad \unicode[STIX]{x1D706}_{{\tilde{y}}}\in \frac{\mathbb{Q}\unicode[STIX]{x1D6FC}_{{\tilde{y}}}\cap \mathbb{X}^{\bullet }}{\mathbb{Z}\unicode[STIX]{x1D6FC}_{{\tilde{y}}}}\mapsto \operatorname{AJ}^{\breve{\mathscr{P}}}({\tilde{y}},\unicode[STIX]{x1D706}_{{\tilde{y}}}),\end{eqnarray}$$
where
![]() $\operatorname{AJ}^{\breve{\mathscr{P}}}$
is the Abel–Jacobi map introduced before. Of course, this map does not really depend on the choice of liftings of
$\operatorname{AJ}^{\breve{\mathscr{P}}}$
is the Abel–Jacobi map introduced before. Of course, this map does not really depend on the choice of liftings of
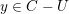 $y\in C-U$
since
$y\in C-U$
since
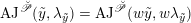 $\operatorname{AJ}^{\breve{\mathscr{P}}}({\tilde{y}},\unicode[STIX]{x1D706}_{{\tilde{y}}})=\operatorname{AJ}^{\breve{\mathscr{P}}}(w{\tilde{y}},w\unicode[STIX]{x1D706}_{{\tilde{y}}})$
.
$\operatorname{AJ}^{\breve{\mathscr{P}}}({\tilde{y}},\unicode[STIX]{x1D706}_{{\tilde{y}}})=\operatorname{AJ}^{\breve{\mathscr{P}}}(w{\tilde{y}},w\unicode[STIX]{x1D706}_{{\tilde{y}}})$
.
Now, as in the proof of Lemma 3.6.1, we have a right exact sequence
 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}(C,\breve{J}^{1}/\breve{J})\rightarrow \unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}})\rightarrow \unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}}^{1})\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}(C,\breve{J}^{1}/\breve{J})\rightarrow \unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}})\rightarrow \unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}}^{1})\rightarrow 0.\end{eqnarray}$$
Since the Abel–Jacobi map induces
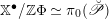 $\mathbb{X}^{\bullet }/\mathbb{Z}\unicode[STIX]{x1D6F7}\simeq \unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}})$
, we deduce that
$\mathbb{X}^{\bullet }/\mathbb{Z}\unicode[STIX]{x1D6F7}\simeq \unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}})$
, we deduce that
 $$\begin{eqnarray}\ker (\unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}})\rightarrow \unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}}^{1}))=\operatorname{Im}(\unicode[STIX]{x1D6E4}(C,\breve{J}^{1}/\breve{J})\rightarrow \unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}}))=\frac{\mathop{\sum }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}}(\mathbb{Q}\unicode[STIX]{x1D6FC}\cap \mathbb{X}^{\bullet })}{\mathbb{Z}\unicode[STIX]{x1D6F7}}.\end{eqnarray}$$
$$\begin{eqnarray}\ker (\unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}})\rightarrow \unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}}^{1}))=\operatorname{Im}(\unicode[STIX]{x1D6E4}(C,\breve{J}^{1}/\breve{J})\rightarrow \unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}}))=\frac{\mathop{\sum }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}}(\mathbb{Q}\unicode[STIX]{x1D6FC}\cap \mathbb{X}^{\bullet })}{\mathbb{Z}\unicode[STIX]{x1D6F7}}.\end{eqnarray}$$
Therefore, (3) follows and the proof of Theorem 3.3.1 is complete.◻
Remark 3.6.2. As a byproduct of the proof, we obtain
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}}^{1})=\frac{\mathbb{X}^{\bullet }}{\mathop{\sum }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}}(\mathbb{Q}\unicode[STIX]{x1D6FC}\cap \mathbb{X}^{\bullet })}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}}^{1})=\frac{\mathbb{X}^{\bullet }}{\mathop{\sum }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}}(\mathbb{Q}\unicode[STIX]{x1D6FC}\cap \mathbb{X}^{\bullet })}.\end{eqnarray}$$
It seems that this expression of
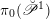 $\unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}}^{1})$
did not appear in literature before.
$\unicode[STIX]{x1D70B}_{0}(\breve{\mathscr{P}}^{1})$
did not appear in literature before.
3.7 A property of
 $\mathfrak{D}_{\text{cl}}$
$\mathfrak{D}_{\text{cl}}$
In this subsection, we assume that
![]() $G$
is semi-simple. We show that the classical duality
$G$
is semi-simple. We show that the classical duality
![]() $\mathfrak{D}_{\text{cl}}$
intertwines certain homomorphisms of Picard stacks over the Hitchin base
$\mathfrak{D}_{\text{cl}}$
intertwines certain homomorphisms of Picard stacks over the Hitchin base
![]() $B^{0}$
. As before, we omit the subscript
$B^{0}$
. As before, we omit the subscript
![]() $^{0}$
.
$^{0}$
.
Let
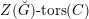 $Z(\breve{G})\text{-}\text{tors}(C)$
denote the Picard stack of
$Z(\breve{G})\text{-}\text{tors}(C)$
denote the Picard stack of
![]() $Z(\breve{G})$
-torsors on
$Z(\breve{G})$
-torsors on
![]() $C$
. We start with the construction of two homomorphisms
$C$
. We start with the construction of two homomorphisms
 $$\begin{eqnarray}\mathfrak{l}_{J}:Z(\breve{G})\text{-}\text{tors}(C)\times B\rightarrow \mathscr{P}^{\vee },\quad \breve{\mathfrak{l}}_{J}:Z(\breve{G})\text{-}\text{tors}(C)\times B\rightarrow \breve{\mathscr{P}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{l}_{J}:Z(\breve{G})\text{-}\text{tors}(C)\times B\rightarrow \mathscr{P}^{\vee },\quad \breve{\mathfrak{l}}_{J}:Z(\breve{G})\text{-}\text{tors}(C)\times B\rightarrow \breve{\mathscr{P}}.\end{eqnarray}$$
The definition of
![]() $\breve{\mathfrak{l}}_{J}$
is easy. It is induced by the natural map of group schemes
$\breve{\mathfrak{l}}_{J}$
is easy. It is induced by the natural map of group schemes
 $$\begin{eqnarray}Z(\breve{G})\times (C\times S)\rightarrow \breve{J}_{b},\end{eqnarray}$$
$$\begin{eqnarray}Z(\breve{G})\times (C\times S)\rightarrow \breve{J}_{b},\end{eqnarray}$$
for every
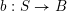 $b:S\rightarrow B$
. For
$b:S\rightarrow B$
. For
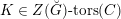 $K\in Z(\breve{G})\text{-}\text{tors}(C)$
, let
$K\in Z(\breve{G})\text{-}\text{tors}(C)$
, let
 $$\begin{eqnarray}K_{J}:=\breve{\mathfrak{l}}_{J}(\{K\}\times B)\in \breve{\mathscr{P}}(B).\end{eqnarray}$$
$$\begin{eqnarray}K_{J}:=\breve{\mathfrak{l}}_{J}(\{K\}\times B)\in \breve{\mathscr{P}}(B).\end{eqnarray}$$
Next we define
![]() $\mathfrak{l}_{J}$
. For the purpose, we need to generalize a construction of [Reference Beilinson and DrinfeldBD91, §4.1]. Let
$\mathfrak{l}_{J}$
. For the purpose, we need to generalize a construction of [Reference Beilinson and DrinfeldBD91, §4.1]. Let
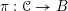 $\unicode[STIX]{x1D70B}:{\mathcal{C}}\rightarrow B$
be a smooth proper relative curve over an affine base
$\unicode[STIX]{x1D70B}:{\mathcal{C}}\rightarrow B$
be a smooth proper relative curve over an affine base
![]() $B$
(later on
$B$
(later on
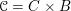 ${\mathcal{C}}=C\times B$
). Let
${\mathcal{C}}=C\times B$
). Let
 $$\begin{eqnarray}0\rightarrow \unicode[STIX]{x1D6F1}(1)\rightarrow \tilde{{\mathcal{G}}}\rightarrow {\mathcal{G}}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \unicode[STIX]{x1D6F1}(1)\rightarrow \tilde{{\mathcal{G}}}\rightarrow {\mathcal{G}}\rightarrow 0\end{eqnarray}$$
be an extension of smooth affine group schemes on
![]() ${\mathcal{C}}$
with
${\mathcal{C}}$
with
![]() $\unicode[STIX]{x1D6F1}$
commutative finite étale. Let
$\unicode[STIX]{x1D6F1}$
commutative finite étale. Let
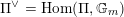 $\unicode[STIX]{x1D6F1}^{\vee }=\operatorname{Hom}(\unicode[STIX]{x1D6F1},\mathbb{G}_{m})$
be its Cartier dual, which is assumed to be étale as well (in particular, the order of
$\unicode[STIX]{x1D6F1}^{\vee }=\operatorname{Hom}(\unicode[STIX]{x1D6F1},\mathbb{G}_{m})$
be its Cartier dual, which is assumed to be étale as well (in particular, the order of
![]() $\unicode[STIX]{x1D6F1}$
is prime to
$\unicode[STIX]{x1D6F1}$
is prime to
![]() $\operatorname{char}~k$
), and let
$\operatorname{char}~k$
), and let
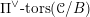 $\unicode[STIX]{x1D6F1}^{\vee }\text{-}\text{tors}({\mathcal{C}}/B)$
denote the Picard stack (over
$\unicode[STIX]{x1D6F1}^{\vee }\text{-}\text{tors}({\mathcal{C}}/B)$
denote the Picard stack (over
![]() $B$
) of
$B$
) of
![]() $\unicode[STIX]{x1D6F1}^{\vee }$
-torsors on
$\unicode[STIX]{x1D6F1}^{\vee }$
-torsors on
![]() ${\mathcal{C}}$
relative to
${\mathcal{C}}$
relative to
![]() $B$
. We construct a Picard functor
$B$
. We construct a Picard functor
 $$\begin{eqnarray}\mathfrak{l}_{{\mathcal{G}}}:\unicode[STIX]{x1D6F1}^{\vee }\text{-}\text{tors}({\mathcal{C}}/B)\rightarrow \operatorname{Pic}\,(\operatorname{Bun}_{{\mathcal{G}}}({\mathcal{C}}/B))\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{l}_{{\mathcal{G}}}:\unicode[STIX]{x1D6F1}^{\vee }\text{-}\text{tors}({\mathcal{C}}/B)\rightarrow \operatorname{Pic}\,(\operatorname{Bun}_{{\mathcal{G}}}({\mathcal{C}}/B))\end{eqnarray}$$
of Picard stacks over
![]() $B$
as follows. First, let
$B$
as follows. First, let
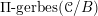 $\unicode[STIX]{x1D6F1}\text{-}\text{gerbes}({\mathcal{C}}/B)$
denote the Picard 2-stack of
$\unicode[STIX]{x1D6F1}\text{-}\text{gerbes}({\mathcal{C}}/B)$
denote the Picard 2-stack of
![]() $\unicode[STIX]{x1D6F1}$
-gerbes on
$\unicode[STIX]{x1D6F1}$
-gerbes on
![]() ${\mathcal{C}}$
relative to
${\mathcal{C}}$
relative to
![]() $B$
, regarded as a Picard stack. Then there is the generalized (or categorical) Chern class map
$B$
, regarded as a Picard stack. Then there is the generalized (or categorical) Chern class map
 $$\begin{eqnarray}\tilde{c}_{{\mathcal{G}}}:\operatorname{Bun}_{{\mathcal{G}}}({\mathcal{C}}/B)\rightarrow \unicode[STIX]{x1D6F1}(1)\text{-}\text{gerbes}({\mathcal{C}}/B)\end{eqnarray}$$
$$\begin{eqnarray}\tilde{c}_{{\mathcal{G}}}:\operatorname{Bun}_{{\mathcal{G}}}({\mathcal{C}}/B)\rightarrow \unicode[STIX]{x1D6F1}(1)\text{-}\text{gerbes}({\mathcal{C}}/B)\end{eqnarray}$$
that assigns every
![]() $B$
-scheme
$B$
-scheme
![]() $S$
and a
$S$
and a
![]() ${\mathcal{G}}$
-torsor
${\mathcal{G}}$
-torsor
![]() $E$
on
$E$
on
![]() ${\mathcal{C}}_{S}$
, the Picard groupoid of the lifting of
${\mathcal{C}}_{S}$
, the Picard groupoid of the lifting of
![]() $E$
to a
$E$
to a
![]() $\tilde{{\mathcal{G}}}$
-torsor. We have the following.
$\tilde{{\mathcal{G}}}$
-torsor. We have the following.
Lemma 3.7.1. The dual of the Picard stack
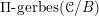 $\unicode[STIX]{x1D6F1}\text{-}\text{gerbes}({\mathcal{C}}/B)$
(as defined in §A.3) is canonically isomorphic to
$\unicode[STIX]{x1D6F1}\text{-}\text{gerbes}({\mathcal{C}}/B)$
(as defined in §A.3) is canonically isomorphic to
 $\unicode[STIX]{x1D6F1}^{\vee }\text{-}\text{tors}({\mathcal{C}}/B)$
.
$\unicode[STIX]{x1D6F1}^{\vee }\text{-}\text{tors}({\mathcal{C}}/B)$
.
We follow [Reference Beilinson and DrinfeldBD91, §4.1.5] for a ‘scientific interpretation’ of this lemma and refer to [Reference Beilinson and DrinfeldBD91, §§4.1.2–4.1.4] for the precise construction. As explained in §A.1, the Picard stack
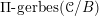 $\unicode[STIX]{x1D6F1}\text{-}\text{gerbes}({\mathcal{C}}/B)$
is incarnated by the complex
$\unicode[STIX]{x1D6F1}\text{-}\text{gerbes}({\mathcal{C}}/B)$
is incarnated by the complex
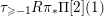 $\unicode[STIX]{x1D70F}_{{\geqslant}-1}R\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6F1}[2](1)$
, and
$\unicode[STIX]{x1D70F}_{{\geqslant}-1}R\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6F1}[2](1)$
, and
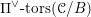 $\unicode[STIX]{x1D6F1}^{\vee }\text{-}\text{tors}({\mathcal{C}}/B)$
is incarnated by the complex
$\unicode[STIX]{x1D6F1}^{\vee }\text{-}\text{tors}({\mathcal{C}}/B)$
is incarnated by the complex
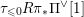 $\unicode[STIX]{x1D70F}_{{\leqslant}0}R\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6F1}^{\vee }[1]$
. Let
$\unicode[STIX]{x1D70F}_{{\leqslant}0}R\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6F1}^{\vee }[1]$
. Let
![]() $\unicode[STIX]{x1D707}_{\infty }^{\prime }$
denote the group of prime-to-
$\unicode[STIX]{x1D707}_{\infty }^{\prime }$
denote the group of prime-to-
![]() $p$
roots of unit. Note that
$p$
roots of unit. Note that
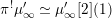 $\unicode[STIX]{x1D70B}^{!}\unicode[STIX]{x1D707}_{\infty }^{\prime }\simeq \unicode[STIX]{x1D707}_{\infty }^{\prime }[2](1)$
. Then by the Verdier duality,
$\unicode[STIX]{x1D70B}^{!}\unicode[STIX]{x1D707}_{\infty }^{\prime }\simeq \unicode[STIX]{x1D707}_{\infty }^{\prime }[2](1)$
. Then by the Verdier duality,
 $$\begin{eqnarray}R\operatorname{Hom}(R\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6F1}[2](1),\unicode[STIX]{x1D707}_{\infty }^{\prime })\simeq R\unicode[STIX]{x1D70B}_{\ast }R\operatorname{Hom}(\unicode[STIX]{x1D6F1}[2](1),\unicode[STIX]{x1D70B}^{!}\unicode[STIX]{x1D707}_{\infty }^{\prime })\simeq R\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6F1}^{\vee }.\end{eqnarray}$$
$$\begin{eqnarray}R\operatorname{Hom}(R\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6F1}[2](1),\unicode[STIX]{x1D707}_{\infty }^{\prime })\simeq R\unicode[STIX]{x1D70B}_{\ast }R\operatorname{Hom}(\unicode[STIX]{x1D6F1}[2](1),\unicode[STIX]{x1D70B}^{!}\unicode[STIX]{x1D707}_{\infty }^{\prime })\simeq R\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6F1}^{\vee }.\end{eqnarray}$$
By shifting by
![]() $[1]$
and truncating
$[1]$
and truncating
![]() $\unicode[STIX]{x1D70F}_{{\leqslant}0}$
, one obtains the lemma. As explained in [Reference Beilinson and DrinfeldBD91, §4.1.5], working in the framework of derived categories is not enough to turn the above heuristics into a proof. One can either give a concrete construction as in [Reference Beilinson and DrinfeldBD91, §§4.1.2–4.1.4] or understand the above argument in the framework of stable
$\unicode[STIX]{x1D70F}_{{\leqslant}0}$
, one obtains the lemma. As explained in [Reference Beilinson and DrinfeldBD91, §4.1.5], working in the framework of derived categories is not enough to turn the above heuristics into a proof. One can either give a concrete construction as in [Reference Beilinson and DrinfeldBD91, §§4.1.2–4.1.4] or understand the above argument in the framework of stable
![]() $\infty$
-categories.
$\infty$
-categories.
Therefore, each
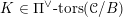 $K\in \unicode[STIX]{x1D6F1}^{\vee }\text{-}\text{tors}({\mathcal{C}}/B)$
defines a morphism
$K\in \unicode[STIX]{x1D6F1}^{\vee }\text{-}\text{tors}({\mathcal{C}}/B)$
defines a morphism
 $$\begin{eqnarray}\mathfrak{l}_{{\mathcal{G}},K}:\operatorname{Bun}_{{\mathcal{G}}}({\mathcal{C}}/B)\stackrel{\tilde{c}_{{\mathcal{G}}}}{\rightarrow }\unicode[STIX]{x1D6F1}(1)\text{-}\text{gerbes}({\mathcal{C}}/B)\stackrel{\langle ,K\rangle }{\rightarrow }B\mathbb{G}_{m}\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{l}_{{\mathcal{G}},K}:\operatorname{Bun}_{{\mathcal{G}}}({\mathcal{C}}/B)\stackrel{\tilde{c}_{{\mathcal{G}}}}{\rightarrow }\unicode[STIX]{x1D6F1}(1)\text{-}\text{gerbes}({\mathcal{C}}/B)\stackrel{\langle ,K\rangle }{\rightarrow }B\mathbb{G}_{m}\end{eqnarray}$$
or equivalently a line bundle
![]() ${\mathcal{L}}_{{\mathcal{G}},K}$
on
${\mathcal{L}}_{{\mathcal{G}},K}$
on
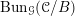 $\operatorname{Bun}_{{\mathcal{G}}}({\mathcal{C}}/B)$
and the assignment
$\operatorname{Bun}_{{\mathcal{G}}}({\mathcal{C}}/B)$
and the assignment
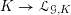 $K\rightarrow {\mathcal{L}}_{{\mathcal{G}},K}$
defines a homomorphism of Picard stacks
$K\rightarrow {\mathcal{L}}_{{\mathcal{G}},K}$
defines a homomorphism of Picard stacks
 $$\begin{eqnarray}\mathfrak{l}_{{\mathcal{G}}}:\unicode[STIX]{x1D6F1}^{\vee }\text{-}\text{tors}({\mathcal{C}}/B)\rightarrow \operatorname{Pic}(\operatorname{Bun}_{{\mathcal{G}}}({\mathcal{C}}/B)),\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{l}_{{\mathcal{G}}}:\unicode[STIX]{x1D6F1}^{\vee }\text{-}\text{tors}({\mathcal{C}}/B)\rightarrow \operatorname{Pic}(\operatorname{Bun}_{{\mathcal{G}}}({\mathcal{C}}/B)),\end{eqnarray}$$
which factors through the
![]() $n$
-torsion of
$n$
-torsion of
 $\operatorname{Pic}(\operatorname{Bun}_{{\mathcal{G}}})({\mathcal{C}}/B)$
where
$\operatorname{Pic}(\operatorname{Bun}_{{\mathcal{G}}})({\mathcal{C}}/B)$
where
![]() $n$
is the order of
$n$
is the order of
![]() $\unicode[STIX]{x1D6F1}^{\vee }$
.
$\unicode[STIX]{x1D6F1}^{\vee }$
.
Note that in the above discussion we do not assume that
![]() ${\mathcal{G}}$
is commutative. But if
${\mathcal{G}}$
is commutative. But if
![]() ${\mathcal{G}}$
is commutative,
${\mathcal{G}}$
is commutative,
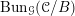 $\operatorname{Bun}_{{\mathcal{G}}}({\mathcal{C}}/B)$
has a natural structure of Picard stack over
$\operatorname{Bun}_{{\mathcal{G}}}({\mathcal{C}}/B)$
has a natural structure of Picard stack over
![]() $B$
and one can check that
$B$
and one can check that
![]() $\mathfrak{l}_{{\mathcal{G}}}$
factors through a homomorphism
$\mathfrak{l}_{{\mathcal{G}}}$
factors through a homomorphism
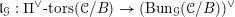 $\mathfrak{l}_{{\mathcal{G}}}:\unicode[STIX]{x1D6F1}^{\vee }\text{-}\text{tors}({\mathcal{C}}/B)\rightarrow (\operatorname{Bun}_{{\mathcal{G}}}({\mathcal{C}}/B))^{\vee }$
.
$\mathfrak{l}_{{\mathcal{G}}}:\unicode[STIX]{x1D6F1}^{\vee }\text{-}\text{tors}({\mathcal{C}}/B)\rightarrow (\operatorname{Bun}_{{\mathcal{G}}}({\mathcal{C}}/B))^{\vee }$
.
Now let
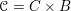 ${\mathcal{C}}=C\times B$
, where
${\mathcal{C}}=C\times B$
, where
![]() $B$
is the Hitchin base as before. Let
$B$
is the Hitchin base as before. Let
![]() ${\mathcal{G}}=J_{b}$
and
${\mathcal{G}}=J_{b}$
and
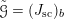 $\tilde{{\mathcal{G}}}=(J_{\text{sc}})_{b}$
, where
$\tilde{{\mathcal{G}}}=(J_{\text{sc}})_{b}$
, where
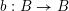 $b:B\rightarrow B$
is the identity map, and
$b:B\rightarrow B$
is the identity map, and
![]() $J_{\text{sc}}$
is the universal regular centralizer for
$J_{\text{sc}}$
is the universal regular centralizer for
![]() $G_{\text{sc}}$
, the simply connected cover of
$G_{\text{sc}}$
, the simply connected cover of
![]() $G$
. Then
$G$
. Then
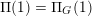 $\unicode[STIX]{x1D6F1}(1)=\unicode[STIX]{x1D6F1}_{G}(1)$
is the fundamental group and
$\unicode[STIX]{x1D6F1}(1)=\unicode[STIX]{x1D6F1}_{G}(1)$
is the fundamental group and
![]() $\unicode[STIX]{x1D6F1}_{G}^{\vee }$
is canonical isomorphic to the center
$\unicode[STIX]{x1D6F1}_{G}^{\vee }$
is canonical isomorphic to the center
![]() $Z(\breve{G})$
of
$Z(\breve{G})$
of
![]() $\breve{G}$
. Therefore, the above construction gives
$\breve{G}$
. Therefore, the above construction gives
![]() $\mathfrak{l}_{J}$
as promised in (3.7.1).
$\mathfrak{l}_{J}$
as promised in (3.7.1).
Note that similarly we can set
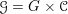 ${\mathcal{G}}=G\times {\mathcal{C}}$
and
${\mathcal{G}}=G\times {\mathcal{C}}$
and
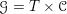 ${\mathcal{G}}=T\times {\mathcal{C}}$
in the above construction so we obtain
${\mathcal{G}}=T\times {\mathcal{C}}$
in the above construction so we obtain
 $$\begin{eqnarray}\mathfrak{l}_{G}:Z(\breve{G})\text{-}\text{tors}(C)\rightarrow \operatorname{Pic}(\operatorname{Bun}_{G}),\quad \mathfrak{l}_{T}:Z(\breve{G})\text{-}\text{tors}(C)\rightarrow (\operatorname{Bun}_{T})^{\vee }.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{l}_{G}:Z(\breve{G})\text{-}\text{tors}(C)\rightarrow \operatorname{Pic}(\operatorname{Bun}_{G}),\quad \mathfrak{l}_{T}:Z(\breve{G})\text{-}\text{tors}(C)\rightarrow (\operatorname{Bun}_{T})^{\vee }.\end{eqnarray}$$
For
 $K\in Z(\breve{G})\text{-}\text{tors}(C)$
, let
$K\in Z(\breve{G})\text{-}\text{tors}(C)$
, let
 ${\mathcal{L}}_{G,K}:=\mathfrak{l}_{G}(K)\in \operatorname{Pic}(\operatorname{Bun}_{G})$
,
${\mathcal{L}}_{G,K}:=\mathfrak{l}_{G}(K)\in \operatorname{Pic}(\operatorname{Bun}_{G})$
,
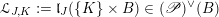 ${\mathcal{L}}_{J,K}:=\mathfrak{l}_{J}(\{K\}\times B)\in (\mathscr{P})^{\vee }(B)$
. The following lemma will be used in §5.6.
${\mathcal{L}}_{J,K}:=\mathfrak{l}_{J}(\{K\}\times B)\in (\mathscr{P})^{\vee }(B)$
. The following lemma will be used in §5.6.
Lemma 3.7.2. Let
![]() $\unicode[STIX]{x1D705}$
be a square root of
$\unicode[STIX]{x1D705}$
be a square root of
![]() $\unicode[STIX]{x1D714}$
. Then the pullback of
$\unicode[STIX]{x1D714}$
. Then the pullback of
![]() ${\mathcal{L}}_{G,K}$
along the map
${\mathcal{L}}_{G,K}$
along the map
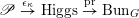 $\mathscr{P}\stackrel{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}}}{\rightarrow }\operatorname{Higgs}\stackrel{\operatorname{pr}}{\rightarrow }\operatorname{Bun}_{G}$
is isomorphic to
$\mathscr{P}\stackrel{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}}}{\rightarrow }\operatorname{Higgs}\stackrel{\operatorname{pr}}{\rightarrow }\operatorname{Bun}_{G}$
is isomorphic to
![]() ${\mathcal{L}}_{J,K}$
, i.e., we have
${\mathcal{L}}_{J,K}$
, i.e., we have
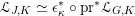 ${\mathcal{L}}_{J,K}\simeq \unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}}^{\ast }\circ \operatorname{pr}^{\ast }{\mathcal{L}}_{G,K}$
.
${\mathcal{L}}_{J,K}\simeq \unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}}^{\ast }\circ \operatorname{pr}^{\ast }{\mathcal{L}}_{G,K}$
.
Proof. It is enough to show that the composition
 $$\begin{eqnarray}\mathscr{P}\stackrel{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}}}{\rightarrow }\operatorname{Higgs}\stackrel{\operatorname{pr}}{\rightarrow }\operatorname{Bun}_{G}\stackrel{\tilde{c}_{G}}{\rightarrow }\unicode[STIX]{x1D6F1}_{G}(1)\text{-}\text{gerbes}(C)\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{P}\stackrel{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}}}{\rightarrow }\operatorname{Higgs}\stackrel{\operatorname{pr}}{\rightarrow }\operatorname{Bun}_{G}\stackrel{\tilde{c}_{G}}{\rightarrow }\unicode[STIX]{x1D6F1}_{G}(1)\text{-}\text{gerbes}(C)\end{eqnarray}$$
is isomorphic to
 $$\begin{eqnarray}\mathscr{P}\stackrel{\tilde{c}_{J}}{\rightarrow }\unicode[STIX]{x1D6F1}_{G}\text{-}\text{gerbes}(C)\times B\rightarrow \unicode[STIX]{x1D6F1}_{G}(1)\text{-}\text{gerbes}(C).\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{P}\stackrel{\tilde{c}_{J}}{\rightarrow }\unicode[STIX]{x1D6F1}_{G}\text{-}\text{gerbes}(C)\times B\rightarrow \unicode[STIX]{x1D6F1}_{G}(1)\text{-}\text{gerbes}(C).\end{eqnarray}$$
Let
![]() $P\in \mathscr{P}$
and
$P\in \mathscr{P}$
and
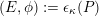 $(E,\unicode[STIX]{x1D719}):=\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}}(P)$
. We need to construct a functorial isomorphism between
$(E,\unicode[STIX]{x1D719}):=\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}}(P)$
. We need to construct a functorial isomorphism between
![]() $\tilde{c}_{J}(P)$
and
$\tilde{c}_{J}(P)$
and
![]() $\tilde{c}_{G}(E)$
where
$\tilde{c}_{G}(E)$
where
![]() $\tilde{c}_{J}(P)$
(respectively
$\tilde{c}_{J}(P)$
(respectively
![]() $\tilde{c}_{G}(E)$
) is the
$\tilde{c}_{G}(E)$
) is the
![]() $\unicode[STIX]{x1D6F1}_{G}(1)$
-gerbe of liftings of
$\unicode[STIX]{x1D6F1}_{G}(1)$
-gerbe of liftings of
![]() $P$
to
$P$
to
![]() $J_{\text{sc}}$
-torsors (respectively
$J_{\text{sc}}$
-torsors (respectively
![]() $G_{\text{sc}}$
-torsors).
$G_{\text{sc}}$
-torsors).
Note that the
![]() $G$
-torsor
$G$
-torsor
![]() $E_{\unicode[STIX]{x1D705}}$
given by the Kostant section has a natural lifting
$E_{\unicode[STIX]{x1D705}}$
given by the Kostant section has a natural lifting
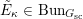 $\tilde{E}_{\unicode[STIX]{x1D705}}\in \operatorname{Bun}_{G_{\text{sc}}}$
, since the cocharacter
$\tilde{E}_{\unicode[STIX]{x1D705}}\in \operatorname{Bun}_{G_{\text{sc}}}$
, since the cocharacter
 $2\unicode[STIX]{x1D70C}:\mathbb{G}_{m}\rightarrow G$
has a natural lifting to
$2\unicode[STIX]{x1D70C}:\mathbb{G}_{m}\rightarrow G$
has a natural lifting to
![]() $G_{\text{sc}}$
. Thus any lifting
$G_{\text{sc}}$
. Thus any lifting
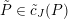 $\tilde{P}\in \tilde{c}_{J}(P)$
defines a lifting
$\tilde{P}\in \tilde{c}_{J}(P)$
defines a lifting
 $\tilde{E}:=\tilde{P}\times ^{J_{\text{sc}}}\tilde{E}_{\unicode[STIX]{x1D705}}\in \operatorname{Bun}_{G_{\text{sc}}}$
of
$\tilde{E}:=\tilde{P}\times ^{J_{\text{sc}}}\tilde{E}_{\unicode[STIX]{x1D705}}\in \operatorname{Bun}_{G_{\text{sc}}}$
of
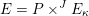 $E=P\times ^{J}E_{\unicode[STIX]{x1D705}}$
and the assignment
$E=P\times ^{J}E_{\unicode[STIX]{x1D705}}$
and the assignment
![]() $\tilde{P}\rightarrow \tilde{E}$
defines a functorial isomorphism between
$\tilde{P}\rightarrow \tilde{E}$
defines a functorial isomorphism between
![]() $\tilde{c}_{J}(P)$
and
$\tilde{c}_{J}(P)$
and
![]() $\tilde{c}_{G}(E)$
. The lemma follows.◻
$\tilde{c}_{G}(E)$
. The lemma follows.◻
We write
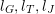 $l_{G},l_{T},l_{J}$
for the induced maps between the corresponding coarse moduli spaces. The following lemma is a specialization of our construction of the duality given in Lemma 3.7.1.
$l_{G},l_{T},l_{J}$
for the induced maps between the corresponding coarse moduli spaces. The following lemma is a specialization of our construction of the duality given in Lemma 3.7.1.
Lemma 3.7.3. Let
![]() $n$
be a positive integer such that
$n$
be a positive integer such that
![]() $p\nmid n$
. Let
$p\nmid n$
. Let
 $$\begin{eqnarray}\mathfrak{l}:\breve{T}[n]\text{-}\text{tors}(C)\rightarrow (\operatorname{Bun}_{T})^{\vee }[n]\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{l}:\breve{T}[n]\text{-}\text{tors}(C)\rightarrow (\operatorname{Bun}_{T})^{\vee }[n]\end{eqnarray}$$
be the tensor functor given by the extension
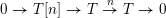 $0\rightarrow T[n]\rightarrow T\stackrel{n}{\rightarrow }T\rightarrow 0$
.Footnote
4
Then the induced map
$0\rightarrow T[n]\rightarrow T\stackrel{n}{\rightarrow }T\rightarrow 0$
.Footnote
4
Then the induced map
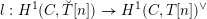 $l:H^{1}(C,\breve{T}[n])\rightarrow H^{1}(C,T[n])^{\vee }$
between the coarse moduli spaces is the same the as map given by the Poincare duality.
$l:H^{1}(C,\breve{T}[n])\rightarrow H^{1}(C,T[n])^{\vee }$
between the coarse moduli spaces is the same the as map given by the Poincare duality.
Now we are ready to state the result in this subsection.
Proposition 3.7.4. There is a natural isomorphism of functors
 $\mathfrak{D}_{\text{cl}}\circ \mathfrak{l}_{J}\simeq \breve{\mathfrak{l}}_{J}$
. In particular, we have
$\mathfrak{D}_{\text{cl}}\circ \mathfrak{l}_{J}\simeq \breve{\mathfrak{l}}_{J}$
. In particular, we have
 $\mathfrak{D}_{\text{cl}}({\mathcal{L}}_{J,K})\simeq K_{J}$
.
$\mathfrak{D}_{\text{cl}}({\mathcal{L}}_{J,K})\simeq K_{J}$
.
Proof. Let
![]() $\breve{G}_{\text{ad}}$
denote the adjoint group of
$\breve{G}_{\text{ad}}$
denote the adjoint group of
![]() $\breve{G}$
. Note that it is the Langlands dual group of
$\breve{G}$
. Note that it is the Langlands dual group of
![]() $G_{\text{sc}}$
. Let
$G_{\text{sc}}$
. Let
![]() $\breve{J}_{\text{ad}}$
be the universal centralizer for
$\breve{J}_{\text{ad}}$
be the universal centralizer for
![]() $\breve{G}_{\text{ad}}$
, and
$\breve{G}_{\text{ad}}$
, and
![]() $\breve{n}_{\text{ad}}$
denote the Picard stack of
$\breve{n}_{\text{ad}}$
denote the Picard stack of
![]() $\breve{J}_{\text{ad}}$
-torsors. We first claim that the composition
$\breve{J}_{\text{ad}}$
-torsors. We first claim that the composition
 $$\begin{eqnarray}Z(\breve{G})\text{-}\text{tors}(C)\times B\stackrel{\mathfrak{l}_{J}}{\rightarrow }\mathscr{P}^{\vee }\stackrel{\mathfrak{D}_{\text{cl}}}{\simeq }\breve{\mathscr{P}}\rightarrow \breve{\mathscr{P}}_{\text{ad}}\end{eqnarray}$$
$$\begin{eqnarray}Z(\breve{G})\text{-}\text{tors}(C)\times B\stackrel{\mathfrak{l}_{J}}{\rightarrow }\mathscr{P}^{\vee }\stackrel{\mathfrak{D}_{\text{cl}}}{\simeq }\breve{\mathscr{P}}\rightarrow \breve{\mathscr{P}}_{\text{ad}}\end{eqnarray}$$
is trivial. From the construction of
![]() $\mathfrak{D}_{\text{cl}}$
, we have the following commutative diagram.
$\mathfrak{D}_{\text{cl}}$
, we have the following commutative diagram.

Thus the above composition can be identified with
 $$\begin{eqnarray}Z(\breve{G})\text{-}\text{tors}(C)\times B\stackrel{\mathfrak{l}_{J}}{\rightarrow }(\mathscr{P})^{\vee }\rightarrow (\mathscr{P}_{\text{sc}})^{\vee }\stackrel{\mathfrak{D}_{\text{cl}}}{\simeq }\breve{\mathscr{P}}_{\text{ad}}.\end{eqnarray}$$
$$\begin{eqnarray}Z(\breve{G})\text{-}\text{tors}(C)\times B\stackrel{\mathfrak{l}_{J}}{\rightarrow }(\mathscr{P})^{\vee }\rightarrow (\mathscr{P}_{\text{sc}})^{\vee }\stackrel{\mathfrak{D}_{\text{cl}}}{\simeq }\breve{\mathscr{P}}_{\text{ad}}.\end{eqnarray}$$
This is trivial since the composition of the first two maps is the dual of
 $$\begin{eqnarray}\mathscr{P}_{\text{sc}}\rightarrow \mathscr{P}\stackrel{\tilde{c}_{J}}{\rightarrow }\unicode[STIX]{x1D6F1}_{G}(1)\text{-}\text{gerbes}(C)\times B,\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{P}_{\text{sc}}\rightarrow \mathscr{P}\stackrel{\tilde{c}_{J}}{\rightarrow }\unicode[STIX]{x1D6F1}_{G}(1)\text{-}\text{gerbes}(C)\times B,\end{eqnarray}$$
which is trivial by the construction of
![]() $\tilde{c}_{J}$
.
$\tilde{c}_{J}$
.
On the other hand, the short exact sequence
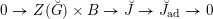 $0\rightarrow Z(\breve{G})\times B\rightarrow \breve{J}\rightarrow \breve{J}_{\text{ad}}\rightarrow 0$
induces a left exact sequence of Picard stacks
$0\rightarrow Z(\breve{G})\times B\rightarrow \breve{J}\rightarrow \breve{J}_{\text{ad}}\rightarrow 0$
induces a left exact sequence of Picard stacks
 $$\begin{eqnarray}0\rightarrow Z(\breve{G})\text{-}\text{tors}(C)\times B\stackrel{\breve{\mathfrak{l}}_{J}}{\rightarrow }\breve{\mathscr{P}}\rightarrow \breve{\mathscr{P}}_{\text{ad}}.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow Z(\breve{G})\text{-}\text{tors}(C)\times B\stackrel{\breve{\mathfrak{l}}_{J}}{\rightarrow }\breve{\mathscr{P}}\rightarrow \breve{\mathscr{P}}_{\text{ad}}.\end{eqnarray}$$
That is,
 $Z(\breve{G})\text{-}\text{tors}(C)\times B$
is identified as the kernel of
$Z(\breve{G})\text{-}\text{tors}(C)\times B$
is identified as the kernel of
 $\breve{\mathscr{P}}\rightarrow \breve{\mathscr{P}}_{\text{ad}}$
. Therefore, there is a morphism
$\breve{\mathscr{P}}\rightarrow \breve{\mathscr{P}}_{\text{ad}}$
. Therefore, there is a morphism
 $$\begin{eqnarray}\mathfrak{i}:Z(\breve{G})\text{-}\text{tors}(C)\times B\rightarrow Z(\breve{G})\text{-}\text{tors}(C)\times B\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{i}:Z(\breve{G})\text{-}\text{tors}(C)\times B\rightarrow Z(\breve{G})\text{-}\text{tors}(C)\times B\end{eqnarray}$$
such that
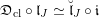 $\mathfrak{D}_{\text{cl}}\circ \mathfrak{l}_{J}\simeq \breve{\mathfrak{l}}_{J}\circ \mathfrak{i}$
. We now show that
$\mathfrak{D}_{\text{cl}}\circ \mathfrak{l}_{J}\simeq \breve{\mathfrak{l}}_{J}\circ \mathfrak{i}$
. We now show that
![]() $\mathfrak{i}$
is isomorphic to the identity morphism. As argued in §3.4, we reduce to show that
$\mathfrak{i}$
is isomorphic to the identity morphism. As argued in §3.4, we reduce to show that
![]() $\mathfrak{i}$
induced the identity map on the coarse moduli space
$\mathfrak{i}$
induced the identity map on the coarse moduli space
 $H^{1}(C,Z(\breve{G}))\times B$
.
$H^{1}(C,Z(\breve{G}))\times B$
.
Let
 $i:H^{1}(C,Z(\breve{G}))\times B\rightarrow H^{1}(C,Z(\breve{G}))\times B$
,
$i:H^{1}(C,Z(\breve{G}))\times B\rightarrow H^{1}(C,Z(\breve{G}))\times B$
,
 $l_{J}:H^{1}(C,Z(\breve{G}))\times B\rightarrow P^{\vee }$
and
$l_{J}:H^{1}(C,Z(\breve{G}))\times B\rightarrow P^{\vee }$
and
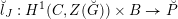 $\breve{l}_{J}:H^{1}(C,Z(\breve{G}))\times B\rightarrow \breve{P}$
be the induced maps on the corresponding coarse moduli spaces. Our goal is to show that
$\breve{l}_{J}:H^{1}(C,Z(\breve{G}))\times B\rightarrow \breve{P}$
be the induced maps on the corresponding coarse moduli spaces. Our goal is to show that
![]() $i=\operatorname{id}$
. Since
$i=\operatorname{id}$
. Since
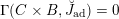 $\unicode[STIX]{x1D6E4}(C\times B,\breve{J}_{\text{ad}})=0$
,
$\unicode[STIX]{x1D6E4}(C\times B,\breve{J}_{\text{ad}})=0$
,
![]() $\breve{l}_{J}$
is injective. Therefore, it suffices to show that
$\breve{l}_{J}$
is injective. Therefore, it suffices to show that
 $$\begin{eqnarray}\breve{l}_{J}\circ (i-\operatorname{id}):H^{1}(C,Z(\breve{G}))\times B\rightarrow \breve{P}\end{eqnarray}$$
$$\begin{eqnarray}\breve{l}_{J}\circ (i-\operatorname{id}):H^{1}(C,Z(\breve{G}))\times B\rightarrow \breve{P}\end{eqnarray}$$
is zero. As in §3.4, we can prove this fiberwise, and therefore we fix
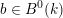 $b\in B^{0}(k)$
. Again, to simplify notations, in the following discussion we write
$b\in B^{0}(k)$
. Again, to simplify notations, in the following discussion we write
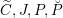 $\widetilde{C},J,P,\breve{P}$
instead of
$\widetilde{C},J,P,\breve{P}$
instead of
 $\widetilde{C}_{b},J_{b},P_{b},\breve{P}_{b}$
, etc.
$\widetilde{C}_{b},J_{b},P_{b},\breve{P}_{b}$
, etc.
Let
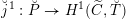 $\breve{j}^{1}:\breve{P}\rightarrow H^{1}(\widetilde{C},\breve{T})$
be the map induced by the morphism
$\breve{j}^{1}:\breve{P}\rightarrow H^{1}(\widetilde{C},\breve{T})$
be the map induced by the morphism
 $\breve{j}^{1}:\unicode[STIX]{x1D70B}^{\ast }\breve{J}\rightarrow \breve{T}$
. Then the composition
$\breve{j}^{1}:\unicode[STIX]{x1D70B}^{\ast }\breve{J}\rightarrow \breve{T}$
. Then the composition
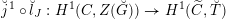 $\breve{j}^{1}\circ \breve{l}_{J}:H^{1}(C,Z(\breve{G}))\rightarrow H^{1}(\widetilde{C},\breve{T})$
is also injective (note that
$\breve{j}^{1}\circ \breve{l}_{J}:H^{1}(C,Z(\breve{G}))\rightarrow H^{1}(\widetilde{C},\breve{T})$
is also injective (note that
![]() $\breve{j}^{1}\circ \breve{l}_{J}$
is induced by the natural map
$\breve{j}^{1}\circ \breve{l}_{J}$
is induced by the natural map
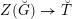 $Z(\breve{G})\rightarrow \breve{T}$
). Thus it is enough to show that
$Z(\breve{G})\rightarrow \breve{T}$
). Thus it is enough to show that
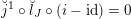 $\breve{j}^{1}\circ \breve{l}_{J}\circ (i-\operatorname{id})=0$
. Since
$\breve{j}^{1}\circ \breve{l}_{J}\circ (i-\operatorname{id})=0$
. Since
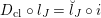 $D_{\text{cl}}\circ l_{J}=\breve{l}_{J}\circ i$
, it is equivalent to show that
$D_{\text{cl}}\circ l_{J}=\breve{l}_{J}\circ i$
, it is equivalent to show that
 $$\begin{eqnarray}\breve{j}^{1}\circ D_{\text{cl}}\circ l_{J}-\breve{j}^{1}\circ \breve{l}_{J}=0.\end{eqnarray}$$
$$\begin{eqnarray}\breve{j}^{1}\circ D_{\text{cl}}\circ l_{J}-\breve{j}^{1}\circ \breve{l}_{J}=0.\end{eqnarray}$$
Let us consider the following diagram

where
![]() $\operatorname{Nm}^{\vee }$
is the dual of (3.1.9), and the right vertical map is
$\operatorname{Nm}^{\vee }$
is the dual of (3.1.9), and the right vertical map is
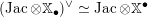 $(\operatorname{Jac}\otimes \mathbb{X}_{\bullet })^{\vee }\simeq \operatorname{Jac}\otimes \mathbb{X}^{\bullet }$
. The right rectangle in the above diagram is commutative by the construction of
$(\operatorname{Jac}\otimes \mathbb{X}_{\bullet })^{\vee }\simeq \operatorname{Jac}\otimes \mathbb{X}^{\bullet }$
. The right rectangle in the above diagram is commutative by the construction of
![]() $D_{\text{cl}}$
in §3. Therefore it is enough to show that the outer diagram is also commutative.
$D_{\text{cl}}$
in §3. Therefore it is enough to show that the outer diagram is also commutative.
Let
![]() $n$
be the order of
$n$
be the order of
![]() $Z(\breve{G})$
. Then
$Z(\breve{G})$
. Then
![]() $\breve{j}^{1}\,\circ \,\breve{l}_{J}$
and
$\breve{j}^{1}\,\circ \,\breve{l}_{J}$
and
 $\operatorname{Nm}^{\vee }\circ \,l_{J}$
will factor through
$\operatorname{Nm}^{\vee }\circ \,l_{J}$
will factor through
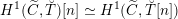 $H^{1}(\widetilde{C},\breve{T})[n]\simeq H^{1}(\widetilde{C},\breve{T}[n])$
and
$H^{1}(\widetilde{C},\breve{T})[n]\simeq H^{1}(\widetilde{C},\breve{T}[n])$
and
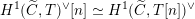 $H^{1}(\widetilde{C},T)^{\vee }[n]\simeq H^{1}(\widetilde{C},T[n])^{\vee }$
.Footnote
5
Thus the outer diagram factors as
$H^{1}(\widetilde{C},T)^{\vee }[n]\simeq H^{1}(\widetilde{C},T[n])^{\vee }$
.Footnote
5
Thus the outer diagram factors as

where the right vertical arrow is now given by the Poincare duality. Unraveling the definition of
![]() $\mathfrak{l}_{J}$
, one sees that
$\mathfrak{l}_{J}$
, one sees that
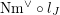 $\operatorname{Nm}^{\vee }\circ l_{J}$
can be identified with
$\operatorname{Nm}^{\vee }\circ l_{J}$
can be identified with
 $$\begin{eqnarray}H^{1}(C,Z(\breve{G}))\stackrel{}{\rightarrow }H^{1}(\widetilde{C},\breve{T}[n])\stackrel{}{\rightarrow }H^{1}(\widetilde{C},T[n])^{\vee }\end{eqnarray}$$
$$\begin{eqnarray}H^{1}(C,Z(\breve{G}))\stackrel{}{\rightarrow }H^{1}(\widetilde{C},\breve{T}[n])\stackrel{}{\rightarrow }H^{1}(\widetilde{C},T[n])^{\vee }\end{eqnarray}$$
where the first map is induced by the natural morphism
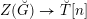 $Z(\breve{G})\rightarrow \breve{T}[n]$
and the second map is the map
$Z(\breve{G})\rightarrow \breve{T}[n]$
and the second map is the map
![]() $l$
in Lemma 3.7.3. Then the commutativity of above diagram follows from Lemma 3.7.3.◻
$l$
in Lemma 3.7.3. Then the commutativity of above diagram follows from Lemma 3.7.3.◻
4 Multiplicative 1-forms
In this section, we establish a technical result. Namely, we show that the pullback of the canonical 1-form
![]() $\unicode[STIX]{x1D703}_{\text{can}}$
on
$\unicode[STIX]{x1D703}_{\text{can}}$
on
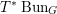 $T^{\ast }\operatorname{Bun}_{G}$
along
$T^{\ast }\operatorname{Bun}_{G}$
along
 $\mathscr{P}\rightarrow T^{\ast }\operatorname{Bun}_{G}$
induced by a Kostant section
$\mathscr{P}\rightarrow T^{\ast }\operatorname{Bun}_{G}$
induced by a Kostant section
![]() $\unicode[STIX]{x1D705}$
is multiplicative in the sense of §C.2.
$\unicode[STIX]{x1D705}$
is multiplicative in the sense of §C.2.
4.1 Lie algebra valued 1-forms
In this subsection, we restrict everything to
![]() $B^{0}$
and therefore omit the subscript
$B^{0}$
and therefore omit the subscript
![]() $^{0}$
from the notation. Recall that there is a group scheme
$^{0}$
from the notation. Recall that there is a group scheme
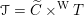 ${\mathcal{T}}=\widetilde{C}\times ^{\text{W}}T$
over
${\mathcal{T}}=\widetilde{C}\times ^{\text{W}}T$
over
![]() $[\widetilde{C}/\text{W}]$
and Proposition 2.5.1 says that there is a homomorphism
$[\widetilde{C}/\text{W}]$
and Proposition 2.5.1 says that there is a homomorphism
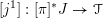 $[j^{1}]:[\unicode[STIX]{x1D70B}]^{\ast }J\rightarrow {\mathcal{T}}$
where
$[j^{1}]:[\unicode[STIX]{x1D70B}]^{\ast }J\rightarrow {\mathcal{T}}$
where
 $[\unicode[STIX]{x1D70B}]:[\widetilde{C}/\text{W}]\rightarrow C\times B$
is the projection. It induces the following commutative diagram.
$[\unicode[STIX]{x1D70B}]:[\widetilde{C}/\text{W}]\rightarrow C\times B$
is the projection. It induces the following commutative diagram.

Note that, due to the product structure on
![]() $C\times B$
, the arrow in the upper row admits a canonical splitting. Therefore, the tautological section in (2.7.1)
$C\times B$
, the arrow in the upper row admits a canonical splitting. Therefore, the tautological section in (2.7.1)
 $$\begin{eqnarray}(\unicode[STIX]{x1D70F}:B\rightarrow B_{J})\in \unicode[STIX]{x1D6E4}(C\times B,\unicode[STIX]{x1D6FA}_{C\times B/B}\otimes \operatorname{Lie}\,J)\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D70F}:B\rightarrow B_{J})\in \unicode[STIX]{x1D6E4}(C\times B,\unicode[STIX]{x1D6FA}_{C\times B/B}\otimes \operatorname{Lie}\,J)\end{eqnarray}$$
can be regarded as a section of
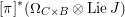 $[\unicode[STIX]{x1D70B}]^{\ast }(\unicode[STIX]{x1D6FA}_{C\times B}\otimes \operatorname{Lie}\,J)$
, which in turn gives
$[\unicode[STIX]{x1D70B}]^{\ast }(\unicode[STIX]{x1D6FA}_{C\times B}\otimes \operatorname{Lie}\,J)$
, which in turn gives
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{\widetilde{C}}\in \unicode[STIX]{x1D6E4}([\widetilde{C}/\text{W}],\unicode[STIX]{x1D6FA}_{[\widetilde{C}/\text{W}]}\otimes \operatorname{Lie}\,{\mathcal{T}})=\unicode[STIX]{x1D6E4}(\widetilde{C},\unicode[STIX]{x1D6FA}_{\widetilde{C}}\otimes \mathfrak{t})^{\text{W}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{\widetilde{C}}\in \unicode[STIX]{x1D6E4}([\widetilde{C}/\text{W}],\unicode[STIX]{x1D6FA}_{[\widetilde{C}/\text{W}]}\otimes \operatorname{Lie}\,{\mathcal{T}})=\unicode[STIX]{x1D6E4}(\widetilde{C},\unicode[STIX]{x1D6FA}_{\widetilde{C}}\otimes \mathfrak{t})^{\text{W}}.\end{eqnarray}$$
We denote by
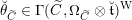 $\breve{\unicode[STIX]{x1D703}}_{\widetilde{C}}\in \unicode[STIX]{x1D6E4}(\widetilde{C},\unicode[STIX]{x1D6FA}_{\widetilde{C}}\otimes \breve{\mathfrak{t}})^{\text{W}}$
the corresponding section for the dual group.
$\breve{\unicode[STIX]{x1D703}}_{\widetilde{C}}\in \unicode[STIX]{x1D6E4}(\widetilde{C},\unicode[STIX]{x1D6FA}_{\widetilde{C}}\otimes \breve{\mathfrak{t}})^{\text{W}}$
the corresponding section for the dual group.
We shall give an alternative description of
![]() $\unicode[STIX]{x1D703}_{\widetilde{C}}$
. We denote by
$\unicode[STIX]{x1D703}_{\widetilde{C}}$
. We denote by
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714}}:\mathfrak{t}_{\unicode[STIX]{x1D714}}\rightarrow \mathfrak{t}_{\unicode[STIX]{x1D714}}\times _{C}\mathfrak{t}_{\unicode[STIX]{x1D714}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714}}:\mathfrak{t}_{\unicode[STIX]{x1D714}}\rightarrow \mathfrak{t}_{\unicode[STIX]{x1D714}}\times _{C}\mathfrak{t}_{\unicode[STIX]{x1D714}}\end{eqnarray}$$
the
![]() $\mathbb{G}_{m}$
-twist by
$\mathbb{G}_{m}$
-twist by
![]() $\unicode[STIX]{x1D714}$
of the map
$\unicode[STIX]{x1D714}$
of the map
![]() $\unicode[STIX]{x1D6FF}$
as in Lemma 2.7.3. We regard
$\unicode[STIX]{x1D6FF}$
as in Lemma 2.7.3. We regard
![]() $\mathfrak{t}_{\unicode[STIX]{x1D714}}$
and
$\mathfrak{t}_{\unicode[STIX]{x1D714}}$
and
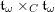 $\mathfrak{t}_{\unicode[STIX]{x1D714}}\times _{C}\mathfrak{t}_{\unicode[STIX]{x1D714}}$
(via the first projection) as schemes over
$\mathfrak{t}_{\unicode[STIX]{x1D714}}\times _{C}\mathfrak{t}_{\unicode[STIX]{x1D714}}$
(via the first projection) as schemes over
![]() $\mathfrak{c}_{\unicode[STIX]{x1D714}}$
and define
$\mathfrak{c}_{\unicode[STIX]{x1D714}}$
and define
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{\widetilde{C}}:\widetilde{C}=e^{\ast }\mathfrak{t}_{\unicode[STIX]{x1D714}}\rightarrow e^{\ast }(\mathfrak{t}_{\unicode[STIX]{x1D714}}\times _{C}\mathfrak{t}_{\unicode[STIX]{x1D714}})=\widetilde{C}\times _{C}(T^{\ast }C\otimes \mathfrak{t})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{\widetilde{C}}:\widetilde{C}=e^{\ast }\mathfrak{t}_{\unicode[STIX]{x1D714}}\rightarrow e^{\ast }(\mathfrak{t}_{\unicode[STIX]{x1D714}}\times _{C}\mathfrak{t}_{\unicode[STIX]{x1D714}})=\widetilde{C}\times _{C}(T^{\ast }C\otimes \mathfrak{t})\end{eqnarray}$$
to be the base change of
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714}}$
via the evaluation map
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714}}$
via the evaluation map
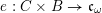 $e:C\times B\rightarrow \mathfrak{c}_{\unicode[STIX]{x1D714}}$
. By Lemma 2.7.3,
$e:C\times B\rightarrow \mathfrak{c}_{\unicode[STIX]{x1D714}}$
. By Lemma 2.7.3,
![]() $\unicode[STIX]{x1D6FF}_{\widetilde{C}}$
is just the pullback of the diagonal map
$\unicode[STIX]{x1D6FF}_{\widetilde{C}}$
is just the pullback of the diagonal map
 $\mathfrak{t}_{\unicode[STIX]{x1D714}}\rightarrow \mathfrak{t}_{\unicode[STIX]{x1D714}}\times _{C}\mathfrak{t}_{\unicode[STIX]{x1D714}}$
along
$\mathfrak{t}_{\unicode[STIX]{x1D714}}\rightarrow \mathfrak{t}_{\unicode[STIX]{x1D714}}\times _{C}\mathfrak{t}_{\unicode[STIX]{x1D714}}$
along
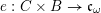 $e:C\times B\rightarrow \mathfrak{c}_{\unicode[STIX]{x1D714}}$
.
$e:C\times B\rightarrow \mathfrak{c}_{\unicode[STIX]{x1D714}}$
.
By construction, the section
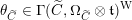 $\unicode[STIX]{x1D703}_{\widetilde{C}}\in \unicode[STIX]{x1D6E4}(\widetilde{C},\unicode[STIX]{x1D6FA}_{\widetilde{C}}\otimes \mathfrak{t})^{\text{W}}$
is equal to the composition
$\unicode[STIX]{x1D703}_{\widetilde{C}}\in \unicode[STIX]{x1D6E4}(\widetilde{C},\unicode[STIX]{x1D6FA}_{\widetilde{C}}\otimes \mathfrak{t})^{\text{W}}$
is equal to the composition
 $$\begin{eqnarray}\widetilde{C}\stackrel{\unicode[STIX]{x1D6FF}_{\widetilde{C}}}{\rightarrow }\widetilde{C}\times _{C}(T^{\ast }C\otimes \mathfrak{t})\rightarrow T^{\ast }\widetilde{C}\otimes \mathfrak{t}\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{C}\stackrel{\unicode[STIX]{x1D6FF}_{\widetilde{C}}}{\rightarrow }\widetilde{C}\times _{C}(T^{\ast }C\otimes \mathfrak{t})\rightarrow T^{\ast }\widetilde{C}\otimes \mathfrak{t}\end{eqnarray}$$
where the last map is the cotangent map for the projection
![]() $\widetilde{C}\rightarrow C$
.
$\widetilde{C}\rightarrow C$
.
The description of
![]() $\unicode[STIX]{x1D703}_{\widetilde{C}}$
in (4.1.2) implies the following relation between
$\unicode[STIX]{x1D703}_{\widetilde{C}}$
in (4.1.2) implies the following relation between
![]() $\unicode[STIX]{x1D703}_{\widetilde{C}}$
and
$\unicode[STIX]{x1D703}_{\widetilde{C}}$
and
![]() $\breve{\unicode[STIX]{x1D703}}_{\widetilde{C}}$
.
$\breve{\unicode[STIX]{x1D703}}_{\widetilde{C}}$
.
Lemma 4.1.1. Let
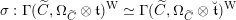 $\unicode[STIX]{x1D70E}:\unicode[STIX]{x1D6E4}(\widetilde{C},\unicode[STIX]{x1D6FA}_{\widetilde{C}}\otimes \mathfrak{t})^{\text{W}}\simeq \unicode[STIX]{x1D6E4}(\widetilde{C},\unicode[STIX]{x1D6FA}_{\widetilde{C}}\otimes \breve{\mathfrak{t}})^{\text{W}}$
be the canonical isomorphism induced by the non-degenerate invariant form
$\unicode[STIX]{x1D70E}:\unicode[STIX]{x1D6E4}(\widetilde{C},\unicode[STIX]{x1D6FA}_{\widetilde{C}}\otimes \mathfrak{t})^{\text{W}}\simeq \unicode[STIX]{x1D6E4}(\widetilde{C},\unicode[STIX]{x1D6FA}_{\widetilde{C}}\otimes \breve{\mathfrak{t}})^{\text{W}}$
be the canonical isomorphism induced by the non-degenerate invariant form
![]() $(\,,\,)$
on
$(\,,\,)$
on
![]() $\mathfrak{t}$
. We have
$\mathfrak{t}$
. We have
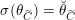 $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703}_{\widetilde{C}})=\breve{\unicode[STIX]{x1D703}}_{\widetilde{C}}$
.
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703}_{\widetilde{C}})=\breve{\unicode[STIX]{x1D703}}_{\widetilde{C}}$
.
Remark 4.1.2. The 1-form
![]() $\unicode[STIX]{x1D703}_{\widetilde{C}}$
is related to the canonical 1-form
$\unicode[STIX]{x1D703}_{\widetilde{C}}$
is related to the canonical 1-form
![]() $\unicode[STIX]{x1D714}_{C}$
of
$\unicode[STIX]{x1D714}_{C}$
of
![]() $C$
in the following way. Let
$C$
in the following way. Let
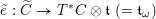 $\tilde{e}:\widetilde{C}\rightarrow T^{\ast }C\otimes \mathfrak{t}~(=\mathfrak{t}_{\unicode[STIX]{x1D714}})$
be the natural
$\tilde{e}:\widetilde{C}\rightarrow T^{\ast }C\otimes \mathfrak{t}~(=\mathfrak{t}_{\unicode[STIX]{x1D714}})$
be the natural
![]() $\text{W}$
-equivariant map (see §2.4). The natural
$\text{W}$
-equivariant map (see §2.4). The natural
![]() $\text{W}$
-equivariant pairing
$\text{W}$
-equivariant pairing
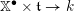 $\mathbb{X}^{\bullet }\times \mathfrak{t}\rightarrow k$
induces a
$\mathbb{X}^{\bullet }\times \mathfrak{t}\rightarrow k$
induces a
![]() $\text{W}$
-equivariant map
$\text{W}$
-equivariant map
 $$\begin{eqnarray}\unicode[STIX]{x1D708}:\widetilde{C}\times \mathbb{X}^{\bullet }\stackrel{\tilde{e}\times \text{id}}{\rightarrow }(T^{\ast }C\otimes \mathfrak{t})\times \mathbb{X}^{\bullet }\rightarrow T^{\ast }C,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D708}:\widetilde{C}\times \mathbb{X}^{\bullet }\stackrel{\tilde{e}\times \text{id}}{\rightarrow }(T^{\ast }C\otimes \mathfrak{t})\times \mathbb{X}^{\bullet }\rightarrow T^{\ast }C,\end{eqnarray}$$
where
![]() $\text{W}$
acts diagonally on
$\text{W}$
acts diagonally on
![]() $\widetilde{C}\times \mathbb{X}^{\bullet }$
. Now the pullback of the canonical 1-form
$\widetilde{C}\times \mathbb{X}^{\bullet }$
. Now the pullback of the canonical 1-form
![]() $\unicode[STIX]{x1D714}_{C}$
on
$\unicode[STIX]{x1D714}_{C}$
on
![]() $T^{\ast }C$
along
$T^{\ast }C$
along
![]() $\unicode[STIX]{x1D708}$
defines a section
$\unicode[STIX]{x1D708}$
defines a section
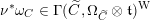 $\unicode[STIX]{x1D708}^{\ast }\unicode[STIX]{x1D714}_{C}\in \unicode[STIX]{x1D6E4}(\widetilde{C},\unicode[STIX]{x1D6FA}_{\widetilde{C}}\otimes \mathfrak{t})^{\text{W}}$
, and using the description of
$\unicode[STIX]{x1D708}^{\ast }\unicode[STIX]{x1D714}_{C}\in \unicode[STIX]{x1D6E4}(\widetilde{C},\unicode[STIX]{x1D6FA}_{\widetilde{C}}\otimes \mathfrak{t})^{\text{W}}$
, and using the description of
![]() $\unicode[STIX]{x1D703}_{\widetilde{C}}$
in (4.1.2) one can check that
$\unicode[STIX]{x1D703}_{\widetilde{C}}$
in (4.1.2) one can check that
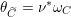 $\unicode[STIX]{x1D703}_{\widetilde{C}}=\unicode[STIX]{x1D708}^{\ast }\unicode[STIX]{x1D714}_{C}$
.
$\unicode[STIX]{x1D703}_{\widetilde{C}}=\unicode[STIX]{x1D708}^{\ast }\unicode[STIX]{x1D714}_{C}$
.
4.2 Canonical 1-form
Let us denote by
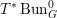 $T^{\ast }\operatorname{Bun}_{G}^{0}$
the maximal smooth open substack of
$T^{\ast }\operatorname{Bun}_{G}^{0}$
the maximal smooth open substack of
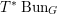 $T^{\ast }\operatorname{Bun}_{G}$
. Then there is a tautological section
$T^{\ast }\operatorname{Bun}_{G}$
. Then there is a tautological section
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{\text{can}}:T^{\ast }\operatorname{Bun}_{G}^{0}\rightarrow T^{\ast }(T^{\ast }\operatorname{Bun}_{G}^{0}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{\text{can}}:T^{\ast }\operatorname{Bun}_{G}^{0}\rightarrow T^{\ast }(T^{\ast }\operatorname{Bun}_{G}^{0}).\end{eqnarray}$$
Note that
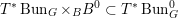 $T^{\ast }\operatorname{Bun}_{G}\times _{B}B^{0}\subset T^{\ast }\operatorname{Bun}_{G}^{0}$
. From now on, we restriction everything to the open part
$T^{\ast }\operatorname{Bun}_{G}\times _{B}B^{0}\subset T^{\ast }\operatorname{Bun}_{G}^{0}$
. From now on, we restriction everything to the open part
![]() $B^{0}$
and therefore will omit
$B^{0}$
and therefore will omit
![]() $^{0}$
from the subscript. Note that for a choice of the Kostant section
$^{0}$
from the subscript. Note that for a choice of the Kostant section
![]() $\unicode[STIX]{x1D705}$
, we have an isomorphism
$\unicode[STIX]{x1D705}$
, we have an isomorphism
 $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}}:\mathscr{P}\simeq T^{\ast }\operatorname{Bun}_{G}$
, and therefore we may regard
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}}:\mathscr{P}\simeq T^{\ast }\operatorname{Bun}_{G}$
, and therefore we may regard
![]() $\unicode[STIX]{x1D703}_{\text{can}}$
as a section
$\unicode[STIX]{x1D703}_{\text{can}}$
as a section
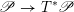 $\mathscr{P}\rightarrow T^{\ast }\mathscr{P}$
, denoted by
$\mathscr{P}\rightarrow T^{\ast }\mathscr{P}$
, denoted by
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
.
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
.
Let
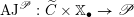 $\operatorname{AJ}^{\mathscr{P}}:\widetilde{C}\times \mathbb{X}_{\bullet }\rightarrow \mathscr{P}$
be the Abel–Jacobi map. Write the pullback as
$\operatorname{AJ}^{\mathscr{P}}:\widetilde{C}\times \mathbb{X}_{\bullet }\rightarrow \mathscr{P}$
be the Abel–Jacobi map. Write the pullback as
 $$\begin{eqnarray}(\operatorname{AJ}^{\mathscr{P}})^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}=\{\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D706}}\}_{\unicode[STIX]{x1D706}\in \mathbb{X}_{\bullet }}\in \unicode[STIX]{x1D6E4}(\widetilde{C}\times \mathbb{X}_{\bullet },\unicode[STIX]{x1D6FA}_{\widetilde{C}})^{\text{W}},\end{eqnarray}$$
$$\begin{eqnarray}(\operatorname{AJ}^{\mathscr{P}})^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}=\{\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D706}}\}_{\unicode[STIX]{x1D706}\in \mathbb{X}_{\bullet }}\in \unicode[STIX]{x1D6E4}(\widetilde{C}\times \mathbb{X}_{\bullet },\unicode[STIX]{x1D6FA}_{\widetilde{C}})^{\text{W}},\end{eqnarray}$$
where
 $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D706}}\in \unicode[STIX]{x1D6E4}(\widetilde{C},\unicode[STIX]{x1D6FA}_{\widetilde{C}})$
is the restriction of
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D706}}\in \unicode[STIX]{x1D6E4}(\widetilde{C},\unicode[STIX]{x1D6FA}_{\widetilde{C}})$
is the restriction of
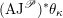 $(\operatorname{AJ}^{\mathscr{P}})^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
to
$(\operatorname{AJ}^{\mathscr{P}})^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
to
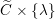 $\widetilde{C}\times \{\unicode[STIX]{x1D706}\}$
. A section
$\widetilde{C}\times \{\unicode[STIX]{x1D706}\}$
. A section
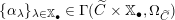 $\{\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}\}_{\unicode[STIX]{x1D706}\in \mathbb{X}_{\bullet }}\in \unicode[STIX]{x1D6E4}(\widetilde{C}\times \mathbb{X}_{\bullet },\unicode[STIX]{x1D6FA}_{\widetilde{C}})$
(respectively
$\{\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}\}_{\unicode[STIX]{x1D706}\in \mathbb{X}_{\bullet }}\in \unicode[STIX]{x1D6E4}(\widetilde{C}\times \mathbb{X}_{\bullet },\unicode[STIX]{x1D6FA}_{\widetilde{C}})$
(respectively
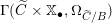 $\unicode[STIX]{x1D6E4}(\widetilde{C}\times \mathbb{X}_{\bullet },\unicode[STIX]{x1D6FA}_{\widetilde{C}/B})$
) is called
$\unicode[STIX]{x1D6E4}(\widetilde{C}\times \mathbb{X}_{\bullet },\unicode[STIX]{x1D6FA}_{\widetilde{C}/B})$
) is called
![]() $\mathbb{X}_{\bullet }$
-multiplicative if it satisfies
$\mathbb{X}_{\bullet }$
-multiplicative if it satisfies
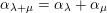 $\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}+\unicode[STIX]{x1D707}}=\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}+\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D707}}$
, for any
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}+\unicode[STIX]{x1D707}}=\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}+\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D707}}$
, for any
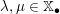 $\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\in \mathbb{X}_{\bullet }$
. Clearly, any
$\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\in \mathbb{X}_{\bullet }$
. Clearly, any
![]() $\mathbb{X}_{\bullet }$
-multiplicative section
$\mathbb{X}_{\bullet }$
-multiplicative section
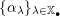 $\{\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}\}_{\unicode[STIX]{x1D706}\in \mathbb{X}_{\bullet }}$
corresponds to a
$\{\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}\}_{\unicode[STIX]{x1D706}\in \mathbb{X}_{\bullet }}$
corresponds to a
![]() $\breve{\mathfrak{t}}$
-valued section
$\breve{\mathfrak{t}}$
-valued section
 $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}(\widetilde{C},\unicode[STIX]{x1D6FA}_{\widetilde{C}}\otimes \breve{\mathfrak{t}})$
(respectively
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}(\widetilde{C},\unicode[STIX]{x1D6FA}_{\widetilde{C}}\otimes \breve{\mathfrak{t}})$
(respectively
 $\unicode[STIX]{x1D6E4}(\widetilde{C},\unicode[STIX]{x1D6FA}_{\widetilde{C}/B}\otimes \breve{\mathfrak{t}})$
). The rest of the section is mainly devoted to the proof of the following result.
$\unicode[STIX]{x1D6E4}(\widetilde{C},\unicode[STIX]{x1D6FA}_{\widetilde{C}/B}\otimes \breve{\mathfrak{t}})$
). The rest of the section is mainly devoted to the proof of the following result.
Proposition 4.2.1. The
![]() $1$
-form
$1$
-form
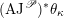 $(\operatorname{AJ}^{\mathscr{P}})^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
is
$(\operatorname{AJ}^{\mathscr{P}})^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
is
![]() $\mathbb{X}_{\bullet }$
-multiplicative. Moreover, if we regard
$\mathbb{X}_{\bullet }$
-multiplicative. Moreover, if we regard
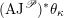 $(\operatorname{AJ}^{\mathscr{P}})^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
as a section of
$(\operatorname{AJ}^{\mathscr{P}})^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
as a section of
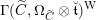 $\unicode[STIX]{x1D6E4}(\widetilde{C},\unicode[STIX]{x1D6FA}_{\widetilde{C}}\otimes \breve{\mathfrak{t}})^{\text{W}}$
, we have
$\unicode[STIX]{x1D6E4}(\widetilde{C},\unicode[STIX]{x1D6FA}_{\widetilde{C}}\otimes \breve{\mathfrak{t}})^{\text{W}}$
, we have
 $$\begin{eqnarray}(\operatorname{AJ}^{\mathscr{P}})^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}=\breve{\unicode[STIX]{x1D703}}_{\widetilde{C}},\end{eqnarray}$$
$$\begin{eqnarray}(\operatorname{AJ}^{\mathscr{P}})^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}=\breve{\unicode[STIX]{x1D703}}_{\widetilde{C}},\end{eqnarray}$$
where
![]() $\breve{\unicode[STIX]{x1D703}}_{\widetilde{C}}$
is the section defined in §4.1.
$\breve{\unicode[STIX]{x1D703}}_{\widetilde{C}}$
is the section defined in §4.1.
We have the following corollary. Recall the notion of multiplicative sections
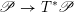 $\mathscr{P}\rightarrow T^{\ast }\mathscr{P}$
as defined in §C.2.
$\mathscr{P}\rightarrow T^{\ast }\mathscr{P}$
as defined in §C.2.
Corollary 4.2.2. The section
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
is multiplicative in the sense of §C.2. In addition, it is independent of the choice of Kostant section
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
is multiplicative in the sense of §C.2. In addition, it is independent of the choice of Kostant section
![]() $\unicode[STIX]{x1D705}$
.
$\unicode[STIX]{x1D705}$
.
Proof. We first show that
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
is multiplicative. Consider the section
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
is multiplicative. Consider the section
 $$\begin{eqnarray}m^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}:\mathscr{P}\times _{B}\mathscr{P}\rightarrow T^{\ast }\mathscr{P}\times _{\mathscr{ P}}(\mathscr{P}\times _{B}\mathscr{P})\rightarrow T^{\ast }(\mathscr{P}\times _{B}\mathscr{P}),\end{eqnarray}$$
$$\begin{eqnarray}m^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}:\mathscr{P}\times _{B}\mathscr{P}\rightarrow T^{\ast }\mathscr{P}\times _{\mathscr{ P}}(\mathscr{P}\times _{B}\mathscr{P})\rightarrow T^{\ast }(\mathscr{P}\times _{B}\mathscr{P}),\end{eqnarray}$$
where the first map is the base change of
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
along the multiplication
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
along the multiplication
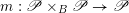 $m:\mathscr{P}\times _{B}\mathscr{P}\rightarrow \mathscr{P}$
, and the second map is the differential
$m:\mathscr{P}\times _{B}\mathscr{P}\rightarrow \mathscr{P}$
, and the second map is the differential
![]() $m_{d}$
of
$m_{d}$
of
![]() $m$
. On the other hand, consider
$m$
. On the other hand, consider
 $$\begin{eqnarray}(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}):\mathscr{P}\times _{B}\mathscr{P}\rightarrow (T^{\ast }\mathscr{P}\times T^{\ast }\mathscr{P})|_{\mathscr{ P}\times _{B}\mathscr{P}}\rightarrow T^{\ast }(\mathscr{P}\times _{B}\mathscr{P}).\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}):\mathscr{P}\times _{B}\mathscr{P}\rightarrow (T^{\ast }\mathscr{P}\times T^{\ast }\mathscr{P})|_{\mathscr{ P}\times _{B}\mathscr{P}}\rightarrow T^{\ast }(\mathscr{P}\times _{B}\mathscr{P}).\end{eqnarray}$$
We need to show that
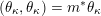 $(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}})=m^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
.
$(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}})=m^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
.
We first have the following lemma, whose proof is independent of Proposition 4.2.1.
Lemma 4.2.3. The projection of
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
along
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
along
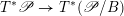 $T^{\ast }\mathscr{P}\rightarrow T^{\ast }(\mathscr{P}/B)$
is multiplicative. More precisely, the images of
$T^{\ast }\mathscr{P}\rightarrow T^{\ast }(\mathscr{P}/B)$
is multiplicative. More precisely, the images of
![]() $m^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
and
$m^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
and
![]() $(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}})$
in
$(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}})$
in
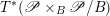 $T^{\ast }(\mathscr{P}\times _{B}\mathscr{P}/B)$
are the same.
$T^{\ast }(\mathscr{P}\times _{B}\mathscr{P}/B)$
are the same.
Proof. Consider the following short exact sequence of vector bundles on
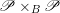 $\mathscr{P}\times _{B}\mathscr{P}$
$\mathscr{P}\times _{B}\mathscr{P}$
 $$\begin{eqnarray}0\rightarrow T^{\ast }B\times _{B}(\mathscr{P}\times _{B}\mathscr{P})\rightarrow T^{\ast }(\mathscr{P}\times _{B}\mathscr{P})\rightarrow T^{\ast }(\mathscr{P}\times _{B}\mathscr{P}/B)\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow T^{\ast }B\times _{B}(\mathscr{P}\times _{B}\mathscr{P})\rightarrow T^{\ast }(\mathscr{P}\times _{B}\mathscr{P})\rightarrow T^{\ast }(\mathscr{P}\times _{B}\mathscr{P}/B)\rightarrow 0.\end{eqnarray}$$
As the projection of
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
along
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
along
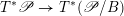 $T^{\ast }\mathscr{P}\rightarrow T^{\ast }(\mathscr{P}/B)$
is identified with
$T^{\ast }\mathscr{P}\rightarrow T^{\ast }(\mathscr{P}/B)$
is identified with
![]() $\unicode[STIX]{x1D70F}^{\ast }\times \operatorname{id}$
(cf. Lemma 2.7.2), the restriction of
$\unicode[STIX]{x1D70F}^{\ast }\times \operatorname{id}$
(cf. Lemma 2.7.2), the restriction of
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
to each fiber
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
to each fiber
![]() $\mathscr{P}_{b}$
is given by the ‘constant’ 1-form
$\mathscr{P}_{b}$
is given by the ‘constant’ 1-form
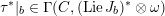 $\unicode[STIX]{x1D70F}^{\ast }|_{b}\in \unicode[STIX]{x1D6E4}(C,(\operatorname{Lie}\,J_{b})^{\ast }\otimes \unicode[STIX]{x1D714})$
. Therefore,
$\unicode[STIX]{x1D70F}^{\ast }|_{b}\in \unicode[STIX]{x1D6E4}(C,(\operatorname{Lie}\,J_{b})^{\ast }\otimes \unicode[STIX]{x1D714})$
. Therefore,
 $(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}})=m^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
in
$(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}})=m^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
in
 $T^{\ast }(\mathscr{P}\times _{B}\mathscr{P}/B)$
.◻
$T^{\ast }(\mathscr{P}\times _{B}\mathscr{P}/B)$
.◻
Therefore, their difference can be regarded as a section
 $$\begin{eqnarray}m^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}-(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}})\in \unicode[STIX]{x1D6E4}(\mathscr{P}\times _{B}\mathscr{P},\operatorname{pr}^{\ast }\unicode[STIX]{x1D6FA}_{B})=(\unicode[STIX]{x1D70B}_{0}(\mathscr{P})\times \unicode[STIX]{x1D70B}_{0}(\mathscr{P}))\times \unicode[STIX]{x1D6E4}(B,\unicode[STIX]{x1D6FA}_{B}).\end{eqnarray}$$
$$\begin{eqnarray}m^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}-(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}})\in \unicode[STIX]{x1D6E4}(\mathscr{P}\times _{B}\mathscr{P},\operatorname{pr}^{\ast }\unicode[STIX]{x1D6FA}_{B})=(\unicode[STIX]{x1D70B}_{0}(\mathscr{P})\times \unicode[STIX]{x1D70B}_{0}(\mathscr{P}))\times \unicode[STIX]{x1D6E4}(B,\unicode[STIX]{x1D6FA}_{B}).\end{eqnarray}$$
The Abel–Jacobi map
 $\operatorname{AJ}^{\mathscr{P}}:\widetilde{C}\times \mathbb{X}_{\bullet }\rightarrow \mathscr{P}$
induces a map
$\operatorname{AJ}^{\mathscr{P}}:\widetilde{C}\times \mathbb{X}_{\bullet }\rightarrow \mathscr{P}$
induces a map
 $$\begin{eqnarray}\operatorname{AJ}^{\mathscr{P},2}:\widetilde{C}\times \mathbb{X}_{\bullet }\times \mathbb{X}_{\bullet }\rightarrow \mathscr{P}\times _{B}\mathscr{P}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{AJ}^{\mathscr{P},2}:\widetilde{C}\times \mathbb{X}_{\bullet }\times \mathbb{X}_{\bullet }\rightarrow \mathscr{P}\times _{B}\mathscr{P}.\end{eqnarray}$$
It is enough to show that the pullback of
 $m^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}-(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}})$
in
$m^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}-(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}})$
in
 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}((\widetilde{C}\times \mathbb{X}_{\bullet }\times \mathbb{X}_{\bullet }),\operatorname{pr}^{\ast }\unicode[STIX]{x1D6FA}_{B})=(\mathbb{X}_{\bullet }\times \mathbb{X}_{\bullet })\times \unicode[STIX]{x1D6E4}(B,\unicode[STIX]{x1D6FA}_{B})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}((\widetilde{C}\times \mathbb{X}_{\bullet }\times \mathbb{X}_{\bullet }),\operatorname{pr}^{\ast }\unicode[STIX]{x1D6FA}_{B})=(\mathbb{X}_{\bullet }\times \mathbb{X}_{\bullet })\times \unicode[STIX]{x1D6E4}(B,\unicode[STIX]{x1D6FA}_{B})\end{eqnarray}$$
vanishes. By Proposition 4.2.1, the one form
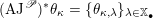 $(\operatorname{AJ}^{\mathscr{P}})^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}=\{\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D706}}\}_{\unicode[STIX]{x1D706}\in \mathbb{X}_{\bullet }}$
is
$(\operatorname{AJ}^{\mathscr{P}})^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}=\{\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D706}}\}_{\unicode[STIX]{x1D706}\in \mathbb{X}_{\bullet }}$
is
![]() $\mathbb{X}_{\bullet }$
-multiplicative, and thus for any
$\mathbb{X}_{\bullet }$
-multiplicative, and thus for any
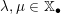 $\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\in \mathbb{X}_{\bullet }$
we have
$\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\in \mathbb{X}_{\bullet }$
we have
 $$\begin{eqnarray}(\operatorname{AJ}^{\mathscr{P},2})^{\ast }(m^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}-(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}))|_{\widetilde{C}\times \{\unicode[STIX]{x1D706}\}\times \{\unicode[STIX]{x1D707}\}}=\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D706}+\unicode[STIX]{x1D707}}-(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D706}}+\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D707}})=0.\end{eqnarray}$$
$$\begin{eqnarray}(\operatorname{AJ}^{\mathscr{P},2})^{\ast }(m^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}-(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}))|_{\widetilde{C}\times \{\unicode[STIX]{x1D706}\}\times \{\unicode[STIX]{x1D707}\}}=\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D706}+\unicode[STIX]{x1D707}}-(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D706}}+\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D707}})=0.\end{eqnarray}$$
This finishes the proof of multiplicative property of
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
. The independence of
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
. The independence of
![]() $\unicode[STIX]{x1D705}$
follows from
$\unicode[STIX]{x1D705}$
follows from
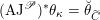 $(\operatorname{AJ}^{\mathscr{P}})^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}=\breve{\unicode[STIX]{x1D703}}_{\widetilde{C}}$
.◻
$(\operatorname{AJ}^{\mathscr{P}})^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}=\breve{\unicode[STIX]{x1D703}}_{\widetilde{C}}$
.◻
Notation. In what follows, we denote the multiplicative 1-form
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
on
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
on
![]() $\mathscr{P}$
by
$\mathscr{P}$
by
![]() $\unicode[STIX]{x1D703}_{m}$
.
$\unicode[STIX]{x1D703}_{m}$
.
Remark 4.2.4. Let
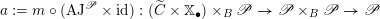 $a:=m\circ (\operatorname{AJ}^{\mathscr{P}}\times \operatorname{id}):(\widetilde{C}\times \mathbb{X}_{\bullet })\times _{B}\mathscr{P}\rightarrow \mathscr{P}\times _{B}\mathscr{P}\rightarrow \mathscr{P}$
be the action map. Then Remark 4.1.2 together with Corollary 4.2.2 implies that
$a:=m\circ (\operatorname{AJ}^{\mathscr{P}}\times \operatorname{id}):(\widetilde{C}\times \mathbb{X}_{\bullet })\times _{B}\mathscr{P}\rightarrow \mathscr{P}\times _{B}\mathscr{P}\rightarrow \mathscr{P}$
be the action map. Then Remark 4.1.2 together with Corollary 4.2.2 implies that
 $$\begin{eqnarray}a^{\ast }\unicode[STIX]{x1D703}_{m}=\breve{\unicode[STIX]{x1D708}}^{\ast }(\unicode[STIX]{x1D714}_{C})\boxtimes \unicode[STIX]{x1D703}_{m}.\end{eqnarray}$$
$$\begin{eqnarray}a^{\ast }\unicode[STIX]{x1D703}_{m}=\breve{\unicode[STIX]{x1D708}}^{\ast }(\unicode[STIX]{x1D714}_{C})\boxtimes \unicode[STIX]{x1D703}_{m}.\end{eqnarray}$$
Here
![]() $\breve{\unicode[STIX]{x1D708}}$
is the map in (4.1.3) for the dual group. In the case of
$\breve{\unicode[STIX]{x1D708}}$
is the map in (4.1.3) for the dual group. In the case of
 $G=\operatorname{GL}_{n}$
, (a variant of) this identity was proved in [Reference Bezrukavnikov and BravermanBB07, Theorem 4.12].
$G=\operatorname{GL}_{n}$
, (a variant of) this identity was proved in [Reference Bezrukavnikov and BravermanBB07, Theorem 4.12].
4.3 Proof of Proposition 4.2.1: first reductions
Let
![]() $\text{}\underline{\unicode[STIX]{x1D703}}_{\unicode[STIX]{x1D705}}$
and
$\text{}\underline{\unicode[STIX]{x1D703}}_{\unicode[STIX]{x1D705}}$
and
![]() $\text{}\underline{\breve{\unicode[STIX]{x1D703}}}_{\widetilde{C}}$
be the projections of
$\text{}\underline{\breve{\unicode[STIX]{x1D703}}}_{\widetilde{C}}$
be the projections of
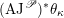 $(\operatorname{AJ}^{\mathscr{P}})^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
and
$(\operatorname{AJ}^{\mathscr{P}})^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
and
![]() $\breve{\unicode[STIX]{x1D703}}_{\widetilde{C}}$
along
$\breve{\unicode[STIX]{x1D703}}_{\widetilde{C}}$
along
 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}(\widetilde{C}\times \mathbb{X}_{\bullet },\unicode[STIX]{x1D6FA}_{\widetilde{C}})\rightarrow \unicode[STIX]{x1D6E4}(\widetilde{C}\times \mathbb{X}_{\bullet },\unicode[STIX]{x1D6FA}_{\widetilde{C}/B}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}(\widetilde{C}\times \mathbb{X}_{\bullet },\unicode[STIX]{x1D6FA}_{\widetilde{C}})\rightarrow \unicode[STIX]{x1D6E4}(\widetilde{C}\times \mathbb{X}_{\bullet },\unicode[STIX]{x1D6FA}_{\widetilde{C}/B}).\end{eqnarray}$$
Lemma 4.2.3 implies that
![]() $\text{}\underline{\unicode[STIX]{x1D703}}_{\unicode[STIX]{x1D705}}$
is
$\text{}\underline{\unicode[STIX]{x1D703}}_{\unicode[STIX]{x1D705}}$
is
![]() $\mathbb{X}_{\bullet }$
-multiplicative and can be regarded as an element in
$\mathbb{X}_{\bullet }$
-multiplicative and can be regarded as an element in
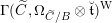 $\unicode[STIX]{x1D6E4}(\widetilde{C},\unicode[STIX]{x1D6FA}_{\widetilde{C}/B}\otimes \breve{\mathfrak{t}})^{\text{W}}$
. Let us first show that
$\unicode[STIX]{x1D6E4}(\widetilde{C},\unicode[STIX]{x1D6FA}_{\widetilde{C}/B}\otimes \breve{\mathfrak{t}})^{\text{W}}$
. Let us first show that
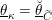 $\text{}\underline{\unicode[STIX]{x1D703}}_{\unicode[STIX]{x1D705}}=\text{}\underline{\breve{\unicode[STIX]{x1D703}}}_{\widetilde{C}}$
.
$\text{}\underline{\unicode[STIX]{x1D703}}_{\unicode[STIX]{x1D705}}=\text{}\underline{\breve{\unicode[STIX]{x1D703}}}_{\widetilde{C}}$
.
Recall in (2.7.4) we have introduced a morphism
 $\unicode[STIX]{x1D704}:\operatorname{Lie}\,J\rightarrow (\operatorname{Lie}\,J)^{\ast }$
. It follows from the definition of
$\unicode[STIX]{x1D704}:\operatorname{Lie}\,J\rightarrow (\operatorname{Lie}\,J)^{\ast }$
. It follows from the definition of
![]() $\unicode[STIX]{x1D704}$
in loc. cit. that the following diagram is commutative
$\unicode[STIX]{x1D704}$
in loc. cit. that the following diagram is commutative

where the arrow in the bottom row is the morphism
 $\operatorname{Lie}\,{\mathcal{T}}\rightarrow \operatorname{Lie}\,\breve{{\mathcal{T}}}$
induced by the invariant from
$\operatorname{Lie}\,{\mathcal{T}}\rightarrow \operatorname{Lie}\,\breve{{\mathcal{T}}}$
induced by the invariant from
![]() $(\,,\,)$
on
$(\,,\,)$
on
![]() $\mathfrak{t}$
. (Recall (cf. §4.1) that
$\mathfrak{t}$
. (Recall (cf. §4.1) that
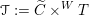 ${\mathcal{T}}:=\widetilde{C}\times ^{W}T$
is a group scheme over
${\mathcal{T}}:=\widetilde{C}\times ^{W}T$
is a group scheme over
![]() $[\widetilde{C}/W]$
and
$[\widetilde{C}/W]$
and
 $[\unicode[STIX]{x1D70B}]:[\widetilde{C}/W]\rightarrow C\times B$
.) It induces the following commutative diagram.
$[\unicode[STIX]{x1D70B}]:[\widetilde{C}/W]\rightarrow C\times B$
.) It induces the following commutative diagram.

Recall the sections
 $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6E4}(C\times B,\unicode[STIX]{x1D6FA}_{C\times B/B}\otimes \operatorname{Lie}\,J)$
and
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6E4}(C\times B,\unicode[STIX]{x1D6FA}_{C\times B/B}\otimes \operatorname{Lie}\,J)$
and
 $\unicode[STIX]{x1D70F}^{\ast }\in \unicode[STIX]{x1D6E4}(C\times B,\unicode[STIX]{x1D6FA}_{C\times B/B}\otimes \operatorname{Lie}\,J^{\ast })$
in §2.7. Note the map
$\unicode[STIX]{x1D70F}^{\ast }\in \unicode[STIX]{x1D6E4}(C\times B,\unicode[STIX]{x1D6FA}_{C\times B/B}\otimes \operatorname{Lie}\,J^{\ast })$
in §2.7. Note the map
![]() $\unicode[STIX]{x1D710}$
in the diagram above is an isomorphismFootnote
6
and it identifies
$\unicode[STIX]{x1D710}$
in the diagram above is an isomorphismFootnote
6
and it identifies
![]() $\text{}\underline{\unicode[STIX]{x1D703}}_{\unicode[STIX]{x1D705}}$
with the section
$\text{}\underline{\unicode[STIX]{x1D703}}_{\unicode[STIX]{x1D705}}$
with the section
![]() $\unicode[STIX]{x1D70F}^{\ast }$
. On the other hand, Lemma 4.1.1 implies the section
$\unicode[STIX]{x1D70F}^{\ast }$
. On the other hand, Lemma 4.1.1 implies the section
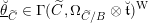 $\text{}\underline{\breve{\unicode[STIX]{x1D703}}}_{\widetilde{C}}\in \unicode[STIX]{x1D6E4}(\widetilde{C},\unicode[STIX]{x1D6FA}_{\widetilde{C}/B}\otimes \breve{\mathfrak{t}})^{\text{W}}$
is equal to the image of
$\text{}\underline{\breve{\unicode[STIX]{x1D703}}}_{\widetilde{C}}\in \unicode[STIX]{x1D6E4}(\widetilde{C},\unicode[STIX]{x1D6FA}_{\widetilde{C}/B}\otimes \breve{\mathfrak{t}})^{\text{W}}$
is equal to the image of
![]() $\unicode[STIX]{x1D70F}$
under the composition of the morphisms in the lower left corner of the above diagram. Thus,
$\unicode[STIX]{x1D70F}$
under the composition of the morphisms in the lower left corner of the above diagram. Thus,
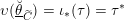 $\unicode[STIX]{x1D710}(\text{}\underline{\breve{\unicode[STIX]{x1D703}}}_{\widetilde{C}})=\unicode[STIX]{x1D704}_{\ast }(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D70F}^{\ast }$
. Therefore both
$\unicode[STIX]{x1D710}(\text{}\underline{\breve{\unicode[STIX]{x1D703}}}_{\widetilde{C}})=\unicode[STIX]{x1D704}_{\ast }(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D70F}^{\ast }$
. Therefore both
![]() $\text{}\underline{\breve{\unicode[STIX]{x1D703}}}_{\widetilde{C}}$
and
$\text{}\underline{\breve{\unicode[STIX]{x1D703}}}_{\widetilde{C}}$
and
![]() $\text{}\underline{\unicode[STIX]{x1D703}}_{\unicode[STIX]{x1D705}}$
map to
$\text{}\underline{\unicode[STIX]{x1D703}}_{\unicode[STIX]{x1D705}}$
map to
![]() $\unicode[STIX]{x1D70F}^{\ast }$
under the isomorphism
$\unicode[STIX]{x1D70F}^{\ast }$
under the isomorphism
![]() $\unicode[STIX]{x1D710}$
, which implies
$\unicode[STIX]{x1D710}$
, which implies
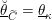 $\text{}\underline{\breve{\unicode[STIX]{x1D703}}}_{\widetilde{C}}=\text{}\underline{\unicode[STIX]{x1D703}}_{\unicode[STIX]{x1D705}}$
.
$\text{}\underline{\breve{\unicode[STIX]{x1D703}}}_{\widetilde{C}}=\text{}\underline{\unicode[STIX]{x1D703}}_{\unicode[STIX]{x1D705}}$
.
As a consequence, difference
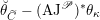 $\breve{\unicode[STIX]{x1D703}}_{\widetilde{C}}-(\operatorname{AJ}^{\mathscr{P}})^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
can be regarded as a section
$\breve{\unicode[STIX]{x1D703}}_{\widetilde{C}}-(\operatorname{AJ}^{\mathscr{P}})^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}$
can be regarded as a section
 $$\begin{eqnarray}\breve{\unicode[STIX]{x1D703}}_{\widetilde{C}}-(\operatorname{AJ}^{\mathscr{P}})^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}\in \unicode[STIX]{x1D6E4}(\widetilde{C}\times \mathbb{X}_{\bullet },\operatorname{pr}^{\ast }\unicode[STIX]{x1D6FA}_{B}).\end{eqnarray}$$
$$\begin{eqnarray}\breve{\unicode[STIX]{x1D703}}_{\widetilde{C}}-(\operatorname{AJ}^{\mathscr{P}})^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}\in \unicode[STIX]{x1D6E4}(\widetilde{C}\times \mathbb{X}_{\bullet },\operatorname{pr}^{\ast }\unicode[STIX]{x1D6FA}_{B}).\end{eqnarray}$$
We need to show that it is zero. Let
![]() $\widetilde{U}\subset \widetilde{C}$
be the largest open subset such that
$\widetilde{U}\subset \widetilde{C}$
be the largest open subset such that
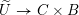 $\widetilde{U}\rightarrow C\times B$
is étale. It is enough to show that
$\widetilde{U}\rightarrow C\times B$
is étale. It is enough to show that
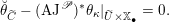 $\breve{\unicode[STIX]{x1D703}}_{\widetilde{C}}-(\operatorname{AJ}^{\mathscr{P}})^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}|_{\widetilde{U}\times \mathbb{X}_{\bullet }}=0.$
Note that for
$\breve{\unicode[STIX]{x1D703}}_{\widetilde{C}}-(\operatorname{AJ}^{\mathscr{P}})^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}|_{\widetilde{U}\times \mathbb{X}_{\bullet }}=0.$
Note that for
![]() $\tilde{x}\in \widetilde{U}$
we have a canonical decomposition
$\tilde{x}\in \widetilde{U}$
we have a canonical decomposition
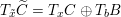 $T_{\tilde{x}}\widetilde{C}=T_{x}C\oplus T_{b}B$
and by (4.3.1) it suffices to show that
$T_{\tilde{x}}\widetilde{C}=T_{x}C\oplus T_{b}B$
and by (4.3.1) it suffices to show that
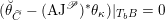 $(\breve{\unicode[STIX]{x1D703}}_{\widetilde{C}}-(\operatorname{AJ}^{\mathscr{P}})^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}})|_{T_{b}B}=0$
. As the section
$(\breve{\unicode[STIX]{x1D703}}_{\widetilde{C}}-(\operatorname{AJ}^{\mathscr{P}})^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}})|_{T_{b}B}=0$
. As the section
![]() $\breve{\unicode[STIX]{x1D703}}_{\widetilde{C}}$
is induced by the canonical splitting
$\breve{\unicode[STIX]{x1D703}}_{\widetilde{C}}$
is induced by the canonical splitting
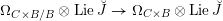 $\unicode[STIX]{x1D6FA}_{C\times B/B}\otimes \operatorname{Lie}\,\breve{J}\rightarrow \unicode[STIX]{x1D6FA}_{C\times B}\otimes \operatorname{Lie}\,\breve{J}$
, the restriction of
$\unicode[STIX]{x1D6FA}_{C\times B/B}\otimes \operatorname{Lie}\,\breve{J}\rightarrow \unicode[STIX]{x1D6FA}_{C\times B}\otimes \operatorname{Lie}\,\breve{J}$
, the restriction of
![]() $\breve{\unicode[STIX]{x1D703}}_{\widetilde{C}}$
to
$\breve{\unicode[STIX]{x1D703}}_{\widetilde{C}}$
to
![]() $T_{b}B$
is zero, so we reduce to show that
$T_{b}B$
is zero, so we reduce to show that
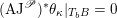 $(\operatorname{AJ}^{\mathscr{P}})^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}|_{T_{b}B}=0$
, i.e., for any
$(\operatorname{AJ}^{\mathscr{P}})^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}|_{T_{b}B}=0$
, i.e., for any
![]() $\unicode[STIX]{x1D706}\in \mathbb{X}_{\bullet }$
and
$\unicode[STIX]{x1D706}\in \mathbb{X}_{\bullet }$
and
 $v\in T_{b}B$
we have
$v\in T_{b}B$
we have
 $$\begin{eqnarray}\langle \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D706}},v\rangle =\langle (\operatorname{AJ}^{\mathscr{P}})^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}|_{\widetilde{C}\times \{\unicode[STIX]{x1D706}\}},v\rangle =0.\end{eqnarray}$$
$$\begin{eqnarray}\langle \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D706}},v\rangle =\langle (\operatorname{AJ}^{\mathscr{P}})^{\ast }\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}|_{\widetilde{C}\times \{\unicode[STIX]{x1D706}\}},v\rangle =0.\end{eqnarray}$$
For the later purpose, we introduce some notations. Let
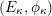 $(E_{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D705}})$
be the Higgs field on
$(E_{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D705}})$
be the Higgs field on
![]() $C\times B$
obtained by the pullback along the Kostant section
$C\times B$
obtained by the pullback along the Kostant section
![]() $\unicode[STIX]{x1D705}$
. For every
$\unicode[STIX]{x1D705}$
. For every
![]() $\unicode[STIX]{x1D706}\in \mathbb{X}_{\bullet }$
let
$\unicode[STIX]{x1D706}\in \mathbb{X}_{\bullet }$
let
 $\operatorname{AJ}^{\mathscr{P},\unicode[STIX]{x1D706}}:\widetilde{C}\rightarrow \mathscr{P}$
denote the corresponding component of the Abel–Jacobi map and let
$\operatorname{AJ}^{\mathscr{P},\unicode[STIX]{x1D706}}:\widetilde{C}\rightarrow \mathscr{P}$
denote the corresponding component of the Abel–Jacobi map and let
 $$\begin{eqnarray}(E_{\tilde{x}},\unicode[STIX]{x1D719}_{\tilde{x}}):=\operatorname{AJ}^{\mathscr{P},\unicode[STIX]{x1D706}}(\tilde{x})\times ^{J_{b}}(E_{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D705}})|_{C\times \{b\}},\end{eqnarray}$$
$$\begin{eqnarray}(E_{\tilde{x}},\unicode[STIX]{x1D719}_{\tilde{x}}):=\operatorname{AJ}^{\mathscr{P},\unicode[STIX]{x1D706}}(\tilde{x})\times ^{J_{b}}(E_{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D705}})|_{C\times \{b\}},\end{eqnarray}$$
be the image of
![]() $\tilde{x}$
under the map
$\tilde{x}$
under the map
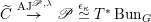 $\widetilde{C}\stackrel{\operatorname{AJ}^{\mathscr{P},\unicode[STIX]{x1D706}}}{\rightarrow }\mathscr{P}\stackrel{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}}}{\simeq }T^{\ast }\operatorname{Bun}_{G}$
. We also define
$\widetilde{C}\stackrel{\operatorname{AJ}^{\mathscr{P},\unicode[STIX]{x1D706}}}{\rightarrow }\mathscr{P}\stackrel{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}}}{\simeq }T^{\ast }\operatorname{Bun}_{G}$
. We also define
 $$\begin{eqnarray}a_{\unicode[STIX]{x1D706}}:\widetilde{C}\stackrel{\operatorname{AJ}^{\mathscr{P},\unicode[STIX]{x1D706}}}{\rightarrow }\mathscr{P}\stackrel{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}}}{\simeq }T^{\ast }\operatorname{Bun}_{G}\rightarrow \operatorname{Bun}_{G}\!.\end{eqnarray}$$
$$\begin{eqnarray}a_{\unicode[STIX]{x1D706}}:\widetilde{C}\stackrel{\operatorname{AJ}^{\mathscr{P},\unicode[STIX]{x1D706}}}{\rightarrow }\mathscr{P}\stackrel{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}}}{\simeq }T^{\ast }\operatorname{Bun}_{G}\rightarrow \operatorname{Bun}_{G}\!.\end{eqnarray}$$
Since
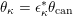 $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}=\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}}^{\ast }\unicode[STIX]{x1D703}_{\text{can}}$
, we have
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705}}=\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}}^{\ast }\unicode[STIX]{x1D703}_{\text{can}}$
, we have
 $$\begin{eqnarray}\langle \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D706}},v\rangle =\langle (\operatorname{AJ}^{\mathscr{P},\unicode[STIX]{x1D706}})^{\ast }\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}}^{\ast }\unicode[STIX]{x1D703}_{\text{can}},v\rangle =\langle \unicode[STIX]{x1D703}_{\text{can}},(\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}})_{\ast }(\operatorname{AJ}^{\mathscr{P},\unicode[STIX]{x1D706}})_{\ast }v\rangle =\langle \unicode[STIX]{x1D719}_{\tilde{x}},{a_{\unicode[STIX]{x1D706}}}_{\ast }v\rangle ,\end{eqnarray}$$
$$\begin{eqnarray}\langle \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D706}},v\rangle =\langle (\operatorname{AJ}^{\mathscr{P},\unicode[STIX]{x1D706}})^{\ast }\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}}^{\ast }\unicode[STIX]{x1D703}_{\text{can}},v\rangle =\langle \unicode[STIX]{x1D703}_{\text{can}},(\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}})_{\ast }(\operatorname{AJ}^{\mathscr{P},\unicode[STIX]{x1D706}})_{\ast }v\rangle =\langle \unicode[STIX]{x1D719}_{\tilde{x}},{a_{\unicode[STIX]{x1D706}}}_{\ast }v\rangle ,\end{eqnarray}$$
where
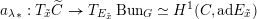 ${a_{\unicode[STIX]{x1D706}}}_{\ast }:T_{\tilde{x}}\widetilde{C}\rightarrow T_{E_{\tilde{x}}}\operatorname{Bun}_{G}\simeq H^{1}(C,\operatorname{ad}E_{\tilde{x}})$
is the differential of
${a_{\unicode[STIX]{x1D706}}}_{\ast }:T_{\tilde{x}}\widetilde{C}\rightarrow T_{E_{\tilde{x}}}\operatorname{Bun}_{G}\simeq H^{1}(C,\operatorname{ad}E_{\tilde{x}})$
is the differential of
![]() $a_{\unicode[STIX]{x1D706}}$
and the last pairing is induced by the Serre duality
$a_{\unicode[STIX]{x1D706}}$
and the last pairing is induced by the Serre duality
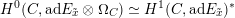 $H^{0}(C,\operatorname{ad}E_{\tilde{x}}\otimes \unicode[STIX]{x1D6FA}_{C})\simeq H^{1}(C,\operatorname{ad}E_{\tilde{x}})^{\ast }$
.
$H^{0}(C,\operatorname{ad}E_{\tilde{x}}\otimes \unicode[STIX]{x1D6FA}_{C})\simeq H^{1}(C,\operatorname{ad}E_{\tilde{x}})^{\ast }$
.
Therefore we reduce to show the following.
Proposition 4.3.1. For any
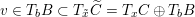 $v\in T_{b}B\subset T_{\tilde{x}}\widetilde{C}=T_{x}C\oplus T_{b}B$
, the pairing
$v\in T_{b}B\subset T_{\tilde{x}}\widetilde{C}=T_{x}C\oplus T_{b}B$
, the pairing
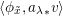 $\langle \unicode[STIX]{x1D719}_{\tilde{x}},{a_{\unicode[STIX]{x1D706}}}_{\ast }v\rangle$
is zero.
$\langle \unicode[STIX]{x1D719}_{\tilde{x}},{a_{\unicode[STIX]{x1D706}}}_{\ast }v\rangle$
is zero.
4.4 Proof of Proposition 4.3.1: calculations of differentials
We shall need several preliminary steps. Recall that there is the
![]() $E_{\unicode[STIX]{x1D705}}$
-twist global Grassmannian
$E_{\unicode[STIX]{x1D705}}$
-twist global Grassmannian
![]() $\operatorname{Gr}(E_{\unicode[STIX]{x1D705}})$
which classify the triples
$\operatorname{Gr}(E_{\unicode[STIX]{x1D705}})$
which classify the triples
 $(x,E,\unicode[STIX]{x1D6FD})$
where
$(x,E,\unicode[STIX]{x1D6FD})$
where
![]() $x\in C$
,
$x\in C$
,
![]() $E$
is a
$E$
is a
![]() $G$
-torsor and
$G$
-torsor and
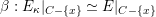 $\unicode[STIX]{x1D6FD}:E_{\unicode[STIX]{x1D705}}|_{C-\{x\}}\simeq E|_{C-\{x\}}$
is an isomorphism. Given a dominant coweight
$\unicode[STIX]{x1D6FD}:E_{\unicode[STIX]{x1D705}}|_{C-\{x\}}\simeq E|_{C-\{x\}}$
is an isomorphism. Given a dominant coweight
![]() $\unicode[STIX]{x1D707}$
(with respect to the set of simple roots we choose), it makes sense to talk about the closed substack
$\unicode[STIX]{x1D707}$
(with respect to the set of simple roots we choose), it makes sense to talk about the closed substack
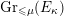 $\operatorname{Gr}_{{\leqslant}\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})$
, consisting of those
$\operatorname{Gr}_{{\leqslant}\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})$
, consisting of those
 $\unicode[STIX]{x1D6FD}:E_{\unicode[STIX]{x1D705}}|_{C-\{x\}}\simeq E|_{C-\{x\}}$
having relative position less than or equal to
$\unicode[STIX]{x1D6FD}:E_{\unicode[STIX]{x1D705}}|_{C-\{x\}}\simeq E|_{C-\{x\}}$
having relative position less than or equal to
![]() $\unicode[STIX]{x1D707}$
at
$\unicode[STIX]{x1D707}$
at
![]() $x$
(cf. [Reference Beilinson and DrinfeldBD91, §5.2.2]). Let
$x$
(cf. [Reference Beilinson and DrinfeldBD91, §5.2.2]). Let
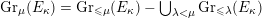 $\operatorname{Gr}_{\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})=\operatorname{Gr}_{{\leqslant}\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})-\bigcup _{\unicode[STIX]{x1D706}<\unicode[STIX]{x1D707}}\operatorname{Gr}_{{\leqslant}\unicode[STIX]{x1D706}}(E_{\unicode[STIX]{x1D705}})$
. We have natural projection maps
$\operatorname{Gr}_{\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})=\operatorname{Gr}_{{\leqslant}\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})-\bigcup _{\unicode[STIX]{x1D706}<\unicode[STIX]{x1D707}}\operatorname{Gr}_{{\leqslant}\unicode[STIX]{x1D706}}(E_{\unicode[STIX]{x1D705}})$
. We have natural projection maps
 $$\begin{eqnarray}\operatorname{Bun}_{G}\stackrel{pr_{1}}{\leftarrow }\operatorname{Gr}_{{\leqslant}\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})\stackrel{pr_{2}}{\rightarrow }C.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Bun}_{G}\stackrel{pr_{1}}{\leftarrow }\operatorname{Gr}_{{\leqslant}\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})\stackrel{pr_{2}}{\rightarrow }C.\end{eqnarray}$$
For any
![]() $x\in C$
, let
$x\in C$
, let
 $$\begin{eqnarray}\operatorname{Gr}_{x}(E_{\unicode[STIX]{x1D705}}):=\operatorname{Gr}(E_{\unicode[STIX]{x1D705}})\times _{C}\{x\},\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Gr}_{x}(E_{\unicode[STIX]{x1D705}}):=\operatorname{Gr}(E_{\unicode[STIX]{x1D705}})\times _{C}\{x\},\end{eqnarray}$$
and similarly we have
 $\operatorname{Gr}_{x,\leqslant \unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}}),\operatorname{Gr}_{x,\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})$
.
$\operatorname{Gr}_{x,\leqslant \unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}}),\operatorname{Gr}_{x,\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})$
.
Note that for any
![]() $\tilde{x}\in \widetilde{C}$
the
$\tilde{x}\in \widetilde{C}$
the
![]() $J$
-torsor
$J$
-torsor
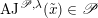 $\operatorname{AJ}^{\mathscr{P},\unicode[STIX]{x1D706}}(\tilde{x})\in \mathscr{P}$
has a canonical trivialization
$\operatorname{AJ}^{\mathscr{P},\unicode[STIX]{x1D706}}(\tilde{x})\in \mathscr{P}$
has a canonical trivialization
![]() $s$
over
$s$
over
![]() $C-x$
(here
$C-x$
(here
![]() $x$
is the image of
$x$
is the image of
![]() $\tilde{x}$
in
$\tilde{x}$
in
![]() $C$
), thus it induces a canonical isomorphism
$C$
), thus it induces a canonical isomorphism
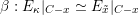 $\unicode[STIX]{x1D6FD}:E_{\unicode[STIX]{x1D705}}|_{C-x}\simeq E_{\tilde{x}}|_{C-x}$
(recall that
$\unicode[STIX]{x1D6FD}:E_{\unicode[STIX]{x1D705}}|_{C-x}\simeq E_{\tilde{x}}|_{C-x}$
(recall that
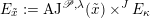 $E_{\tilde{x}}:=\operatorname{AJ}^{\mathscr{P},\unicode[STIX]{x1D706}}(\tilde{x})\times ^{J}E_{\unicode[STIX]{x1D705}}$
). The assignment
$E_{\tilde{x}}:=\operatorname{AJ}^{\mathscr{P},\unicode[STIX]{x1D706}}(\tilde{x})\times ^{J}E_{\unicode[STIX]{x1D705}}$
). The assignment
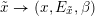 $\tilde{x}\rightarrow (x,E_{\tilde{x}},\unicode[STIX]{x1D6FD})$
defines a morphism
$\tilde{x}\rightarrow (x,E_{\tilde{x}},\unicode[STIX]{x1D6FD})$
defines a morphism
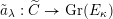 $\tilde{a}_{\unicode[STIX]{x1D706}}:\widetilde{C}\rightarrow \operatorname{Gr}(E_{\unicode[STIX]{x1D705}})$
. We have the following key lemma.
$\tilde{a}_{\unicode[STIX]{x1D706}}:\widetilde{C}\rightarrow \operatorname{Gr}(E_{\unicode[STIX]{x1D705}})$
. We have the following key lemma.
Lemma 4.4.1. Let
![]() $\unicode[STIX]{x1D707}$
be a dominant coweight and
$\unicode[STIX]{x1D707}$
be a dominant coweight and
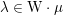 $\unicode[STIX]{x1D706}\in \text{W}\cdot \unicode[STIX]{x1D707}$
. The morphism
$\unicode[STIX]{x1D706}\in \text{W}\cdot \unicode[STIX]{x1D707}$
. The morphism
![]() $\tilde{a}_{\unicode[STIX]{x1D706}}$
factors through
$\tilde{a}_{\unicode[STIX]{x1D706}}$
factors through
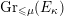 $\operatorname{Gr}_{{\leqslant}\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})$
, and the following diagram
$\operatorname{Gr}_{{\leqslant}\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})$
, and the following diagram

is commutative. Moreover, for any
![]() $k$
-point
$k$
-point
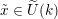 $\tilde{x}\in \widetilde{U}(k)$
,
$\tilde{x}\in \widetilde{U}(k)$
,
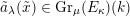 $\tilde{a}_{\unicode[STIX]{x1D706}}(\tilde{x})\in \operatorname{Gr}_{\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})(k)$
.
$\tilde{a}_{\unicode[STIX]{x1D706}}(\tilde{x})\in \operatorname{Gr}_{\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})(k)$
.
The proof is given at the end of this subsection. We also need the following lemma about the differential of
![]() $\tilde{a}_{\unicode[STIX]{x1D706}}$
.
$\tilde{a}_{\unicode[STIX]{x1D706}}$
.
Lemma 4.4.2. Let
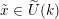 $\tilde{x}\in \widetilde{U}(k)$
, and let
$\tilde{x}\in \widetilde{U}(k)$
, and let
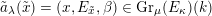 $\tilde{a}_{\unicode[STIX]{x1D706}}(\tilde{x})=(x,E_{\tilde{x}},\unicode[STIX]{x1D6FD})\in \operatorname{Gr}_{\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})(k)$
(by Lemma 4.4.1). For every
$\tilde{a}_{\unicode[STIX]{x1D706}}(\tilde{x})=(x,E_{\tilde{x}},\unicode[STIX]{x1D6FD})\in \operatorname{Gr}_{\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})(k)$
(by Lemma 4.4.1). For every
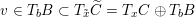 $v\in T_{b}B\subset T_{\tilde{x}}\widetilde{C}=T_{x}C\oplus T_{b}B$
, we have
$v\in T_{b}B\subset T_{\tilde{x}}\widetilde{C}=T_{x}C\oplus T_{b}B$
, we have
 $$\begin{eqnarray}u:=(\tilde{a}_{\unicode[STIX]{x1D706}})_{\ast }v\in T_{(E_{\tilde{x}},\unicode[STIX]{x1D6FD})}\operatorname{Gr}_{x,\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})\subset T_{(x,E_{\tilde{x}},\unicode[STIX]{x1D6FD})}\operatorname{Gr}_{\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}}).\end{eqnarray}$$
$$\begin{eqnarray}u:=(\tilde{a}_{\unicode[STIX]{x1D706}})_{\ast }v\in T_{(E_{\tilde{x}},\unicode[STIX]{x1D6FD})}\operatorname{Gr}_{x,\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})\subset T_{(x,E_{\tilde{x}},\unicode[STIX]{x1D6FD})}\operatorname{Gr}_{\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}}).\end{eqnarray}$$
Proof. The subspace
 $T_{(E_{\tilde{x}},\unicode[STIX]{x1D6FD})}\operatorname{Gr}_{x,\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})\subset T_{(x,E_{\tilde{x}},\unicode[STIX]{x1D6FD})}\operatorname{Gr}_{\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})$
is equal to
$T_{(E_{\tilde{x}},\unicode[STIX]{x1D6FD})}\operatorname{Gr}_{x,\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})\subset T_{(x,E_{\tilde{x}},\unicode[STIX]{x1D6FD})}\operatorname{Gr}_{\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})$
is equal to
 $$\begin{eqnarray}\operatorname{Ker}((pr_{2})_{\ast }:T_{(x,E_{\tilde{x}},\unicode[STIX]{x1D6FD})}\operatorname{Gr}_{\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})\rightarrow T_{x}C).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Ker}((pr_{2})_{\ast }:T_{(x,E_{\tilde{x}},\unicode[STIX]{x1D6FD})}\operatorname{Gr}_{\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})\rightarrow T_{x}C).\end{eqnarray}$$
Therefore it is enough to show
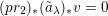 $(pr_{2})_{\ast }(\tilde{a}_{\unicode[STIX]{x1D706}})_{\ast }v=0$
. Recall that we have the following commutative diagram (not Cartesian).
$(pr_{2})_{\ast }(\tilde{a}_{\unicode[STIX]{x1D706}})_{\ast }v=0$
. Recall that we have the following commutative diagram (not Cartesian).

Thus we have
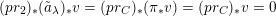 $(pr_{2})_{\ast }(\tilde{a}_{\unicode[STIX]{x1D706}})_{\ast }v=(pr_{C})_{\ast }(\unicode[STIX]{x1D70B}_{\ast }v)=(pr_{C})_{\ast }v=0$
. This finishes the proof.◻
$(pr_{2})_{\ast }(\tilde{a}_{\unicode[STIX]{x1D706}})_{\ast }v=(pr_{C})_{\ast }(\unicode[STIX]{x1D70B}_{\ast }v)=(pr_{C})_{\ast }v=0$
. This finishes the proof.◻
Combining the above two lemmas we obtain that
 $$\begin{eqnarray}\langle \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D706}},v\rangle =\langle \unicode[STIX]{x1D719}_{\tilde{x}},{a_{\unicode[STIX]{x1D706}}}_{\ast }v\rangle =\langle \unicode[STIX]{x1D719}_{\tilde{x}},(pr_{1})_{\ast }u\rangle\end{eqnarray}$$
$$\begin{eqnarray}\langle \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D706}},v\rangle =\langle \unicode[STIX]{x1D719}_{\tilde{x}},{a_{\unicode[STIX]{x1D706}}}_{\ast }v\rangle =\langle \unicode[STIX]{x1D719}_{\tilde{x}},(pr_{1})_{\ast }u\rangle\end{eqnarray}$$
where
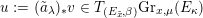 $u:=(\tilde{a}_{\unicode[STIX]{x1D706}})_{\ast }v\in T_{(E_{\tilde{x}},\unicode[STIX]{x1D6FD})}\operatorname{Gr}_{x,\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})$
. So we need show that the last pairing is zero. To calculate it, we need a few more notations. For any
$u:=(\tilde{a}_{\unicode[STIX]{x1D706}})_{\ast }v\in T_{(E_{\tilde{x}},\unicode[STIX]{x1D6FD})}\operatorname{Gr}_{x,\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})$
. So we need show that the last pairing is zero. To calculate it, we need a few more notations. For any
![]() $x\in C$
we denote by
$x\in C$
we denote by
![]() ${\mathcal{O}}_{x}$
the completion of the local ring of
${\mathcal{O}}_{x}$
the completion of the local ring of
![]() $C$
at
$C$
at
![]() $x$
and
$x$
and
![]() $F_{x}$
its fractional field. Let
$F_{x}$
its fractional field. Let
![]() $\unicode[STIX]{x1D714}_{{\mathcal{O}}_{x}}$
(respectively
$\unicode[STIX]{x1D714}_{{\mathcal{O}}_{x}}$
(respectively
![]() $\unicode[STIX]{x1D714}_{F_{x}}$
) denote the completed regular (respectively rational) differentials on
$\unicode[STIX]{x1D714}_{F_{x}}$
) denote the completed regular (respectively rational) differentials on
![]() $\operatorname{Spec}{\mathcal{O}}_{x}$
. We denote by
$\operatorname{Spec}{\mathcal{O}}_{x}$
. We denote by
 $$\begin{eqnarray}\operatorname{Res}(\,,\,):\mathfrak{g}(\unicode[STIX]{x1D714}_{F_{x}})\times \mathfrak{g}(F_{x})\rightarrow k\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Res}(\,,\,):\mathfrak{g}(\unicode[STIX]{x1D714}_{F_{x}})\times \mathfrak{g}(F_{x})\rightarrow k\end{eqnarray}$$
the residue pairing induced by the
![]() $G$
-invariant form
$G$
-invariant form
![]() $(\,,\,)$
on
$(\,,\,)$
on
![]() $\mathfrak{g}$
.
$\mathfrak{g}$
.
Let us fix a trivialization
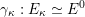 $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D705}}:E_{\unicode[STIX]{x1D705}}\simeq E^{0}$
on
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D705}}:E_{\unicode[STIX]{x1D705}}\simeq E^{0}$
on
![]() $\operatorname{Spec}{\mathcal{O}}_{x}$
. Then, for every trivialization
$\operatorname{Spec}{\mathcal{O}}_{x}$
. Then, for every trivialization
![]() $\unicode[STIX]{x1D6FE}$
of
$\unicode[STIX]{x1D6FE}$
of
![]() $E$
on
$E$
on
![]() $\operatorname{Spec}{\mathcal{O}}_{x}$
, we obtain
$\operatorname{Spec}{\mathcal{O}}_{x}$
, we obtain
 $$\begin{eqnarray}g=\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D705}}^{-1}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\in G(F_{x}).\end{eqnarray}$$
$$\begin{eqnarray}g=\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D705}}^{-1}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\in G(F_{x}).\end{eqnarray}$$
In this way,
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D705}}$
induces an isomorphism
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D705}}$
induces an isomorphism
 $$\begin{eqnarray}\operatorname{Gr}_{x,\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})\simeq \operatorname{Orb}_{\unicode[STIX]{x1D707}},\quad (E,\unicode[STIX]{x1D6FD})\mapsto \unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D705}}^{-1}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}G({\mathcal{O}}_{x}),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Gr}_{x,\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})\simeq \operatorname{Orb}_{\unicode[STIX]{x1D707}},\quad (E,\unicode[STIX]{x1D6FD})\mapsto \unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D705}}^{-1}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}G({\mathcal{O}}_{x}),\end{eqnarray}$$
where
![]() $\operatorname{Orb}_{\unicode[STIX]{x1D707}}$
is the
$\operatorname{Orb}_{\unicode[STIX]{x1D707}}$
is the
![]() $G({\mathcal{O}}_{x})$
-orbit of
$G({\mathcal{O}}_{x})$
-orbit of
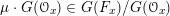 $\unicode[STIX]{x1D707}\cdot G({\mathcal{O}}_{x})\in G(F_{x})/G({\mathcal{O}}_{x})$
. Under the isomorphism, we have the identification of the tangent spaces
$\unicode[STIX]{x1D707}\cdot G({\mathcal{O}}_{x})\in G(F_{x})/G({\mathcal{O}}_{x})$
. Under the isomorphism, we have the identification of the tangent spaces
 $$\begin{eqnarray}T_{(E,\unicode[STIX]{x1D6FD})}\operatorname{Gr}_{x,\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})\simeq \mathfrak{g}({\mathcal{O}}_{x})/(\operatorname{Ad}_{g}\mathfrak{g}({\mathcal{O}}_{x})\cap \mathfrak{g}({\mathcal{O}}_{x})).\end{eqnarray}$$
$$\begin{eqnarray}T_{(E,\unicode[STIX]{x1D6FD})}\operatorname{Gr}_{x,\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})\simeq \mathfrak{g}({\mathcal{O}}_{x})/(\operatorname{Ad}_{g}\mathfrak{g}({\mathcal{O}}_{x})\cap \mathfrak{g}({\mathcal{O}}_{x})).\end{eqnarray}$$
For any
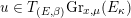 $u\in T_{(E,\unicode[STIX]{x1D6FD})}\operatorname{Gr}_{x,\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})$
and
$u\in T_{(E,\unicode[STIX]{x1D6FD})}\operatorname{Gr}_{x,\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})$
and
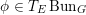 $\unicode[STIX]{x1D719}\in T_{E}\operatorname{Bun}_{G}$
the pairing
$\unicode[STIX]{x1D719}\in T_{E}\operatorname{Bun}_{G}$
the pairing
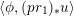 $\langle \unicode[STIX]{x1D719},(pr_{1})_{\ast }u\rangle$
can be calculated as follows. Let
$\langle \unicode[STIX]{x1D719},(pr_{1})_{\ast }u\rangle$
can be calculated as follows. Let
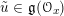 $\tilde{u} \in \mathfrak{g}({\mathcal{O}}_{x})$
be a lifting of
$\tilde{u} \in \mathfrak{g}({\mathcal{O}}_{x})$
be a lifting of
![]() $u$
under the above isomorphism. Let
$u$
under the above isomorphism. Let
![]() $\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FE})$
denote the
$\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FE})$
denote the
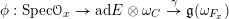 $\unicode[STIX]{x1D719}:\operatorname{Spec}{\mathcal{O}}_{x}\rightarrow \operatorname{ad}E\otimes \unicode[STIX]{x1D714}_{C}\stackrel{\unicode[STIX]{x1D6FE}}{\rightarrow }\mathfrak{g}(\unicode[STIX]{x1D714}_{F_{x}})$
. Now we have
$\unicode[STIX]{x1D719}:\operatorname{Spec}{\mathcal{O}}_{x}\rightarrow \operatorname{ad}E\otimes \unicode[STIX]{x1D714}_{C}\stackrel{\unicode[STIX]{x1D6FE}}{\rightarrow }\mathfrak{g}(\unicode[STIX]{x1D714}_{F_{x}})$
. Now we have
 $$\begin{eqnarray}\langle \unicode[STIX]{x1D719},(pr_{1})_{\ast }u\rangle =\operatorname{Res}(\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FE}),\operatorname{Ad}_{g}^{-1}\tilde{u} ).\end{eqnarray}$$
$$\begin{eqnarray}\langle \unicode[STIX]{x1D719},(pr_{1})_{\ast }u\rangle =\operatorname{Res}(\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FE}),\operatorname{Ad}_{g}^{-1}\tilde{u} ).\end{eqnarray}$$
In our case
 $\unicode[STIX]{x1D719}=\unicode[STIX]{x1D719}_{\tilde{x}}=\operatorname{AJ}^{\mathscr{P},\unicode[STIX]{x1D706}}(\tilde{x})\times ^{J}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D705}}$
, the following lemma will imply the vanishing of
$\unicode[STIX]{x1D719}=\unicode[STIX]{x1D719}_{\tilde{x}}=\operatorname{AJ}^{\mathscr{P},\unicode[STIX]{x1D706}}(\tilde{x})\times ^{J}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D705}}$
, the following lemma will imply the vanishing of
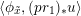 $\langle \unicode[STIX]{x1D719}_{\tilde{x}},(pr_{1})_{\ast }u\rangle$
, and therefore will finish the proof of Proposition 4.3.1.
$\langle \unicode[STIX]{x1D719}_{\tilde{x}},(pr_{1})_{\ast }u\rangle$
, and therefore will finish the proof of Proposition 4.3.1.
Lemma 4.4.3. We have
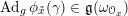 $\operatorname{Ad}_{g}\unicode[STIX]{x1D719}_{\tilde{x}}(\unicode[STIX]{x1D6FE})\in \mathfrak{g}(\unicode[STIX]{x1D714}_{{\mathcal{O}}_{x}})$
.
$\operatorname{Ad}_{g}\unicode[STIX]{x1D719}_{\tilde{x}}(\unicode[STIX]{x1D6FE})\in \mathfrak{g}(\unicode[STIX]{x1D714}_{{\mathcal{O}}_{x}})$
.
Proof. Indeed, unraveling the definitions, we have
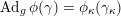 $\operatorname{Ad}_{g}\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D705}}(\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D705}})$
, which is regular.◻
$\operatorname{Ad}_{g}\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D705}}(\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D705}})$
, which is regular.◻
It remains to prove Lemma 4.4.1. Let
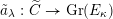 $\tilde{a}_{\unicode[STIX]{x1D706}}:\widetilde{C}\rightarrow \operatorname{Gr}(E_{\unicode[STIX]{x1D705}})$
be the morphism constructed as in the lemma. Since
$\tilde{a}_{\unicode[STIX]{x1D706}}:\widetilde{C}\rightarrow \operatorname{Gr}(E_{\unicode[STIX]{x1D705}})$
be the morphism constructed as in the lemma. Since
![]() $\widetilde{C}$
is smooth and
$\widetilde{C}$
is smooth and
![]() $\widetilde{U}\subset \widetilde{C}$
is open dense, it is enough to show that
$\widetilde{U}\subset \widetilde{C}$
is open dense, it is enough to show that
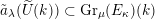 $\tilde{a}_{\unicode[STIX]{x1D706}}(\widetilde{U}(k))\subset \operatorname{Gr}_{\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})(k)$
. Let
$\tilde{a}_{\unicode[STIX]{x1D706}}(\widetilde{U}(k))\subset \operatorname{Gr}_{\unicode[STIX]{x1D707}}(E_{\unicode[STIX]{x1D705}})(k)$
. Let
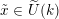 $\tilde{x}\in \widetilde{U}(k)$
and
$\tilde{x}\in \widetilde{U}(k)$
and
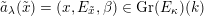 $\tilde{a}_{\unicode[STIX]{x1D706}}(\tilde{x})=(x,E_{\tilde{x}},\unicode[STIX]{x1D6FD})\in \operatorname{Gr}(E_{\unicode[STIX]{x1D705}})(k)$
be its image, where
$\tilde{a}_{\unicode[STIX]{x1D706}}(\tilde{x})=(x,E_{\tilde{x}},\unicode[STIX]{x1D6FD})\in \operatorname{Gr}(E_{\unicode[STIX]{x1D705}})(k)$
be its image, where
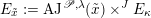 $E_{\tilde{x}}:=\operatorname{AJ}^{\mathscr{P},\unicode[STIX]{x1D706}}(\tilde{x})\times ^{J}E_{\unicode[STIX]{x1D705}}$
and
$E_{\tilde{x}}:=\operatorname{AJ}^{\mathscr{P},\unicode[STIX]{x1D706}}(\tilde{x})\times ^{J}E_{\unicode[STIX]{x1D705}}$
and
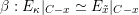 $\unicode[STIX]{x1D6FD}:E_{\unicode[STIX]{x1D705}}|_{C-x}\simeq E_{\tilde{x}}|_{C-x}$
is the isomorphism induced by the canonical section
$\unicode[STIX]{x1D6FD}:E_{\unicode[STIX]{x1D705}}|_{C-x}\simeq E_{\tilde{x}}|_{C-x}$
is the isomorphism induced by the canonical section
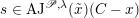 $s\in \operatorname{AJ}^{\mathscr{P},\unicode[STIX]{x1D706}}(\tilde{x})(C-x)$
. Let
$s\in \operatorname{AJ}^{\mathscr{P},\unicode[STIX]{x1D706}}(\tilde{x})(C-x)$
. Let
 $$\begin{eqnarray}\text{rel}:\operatorname{Gr}_{x}(E_{\unicode[STIX]{x1D705}})\rightarrow \mathbb{X}_{\bullet }/\text{W}\end{eqnarray}$$
$$\begin{eqnarray}\text{rel}:\operatorname{Gr}_{x}(E_{\unicode[STIX]{x1D705}})\rightarrow \mathbb{X}_{\bullet }/\text{W}\end{eqnarray}$$
be the map sending an element
![]() $(E,\unicode[STIX]{x1D6FD})$
to the relative position of
$(E,\unicode[STIX]{x1D6FD})$
to the relative position of
![]() $\unicode[STIX]{x1D6FD}$
(cf. [Reference Beilinson and DrinfeldBD91, §5.2.2]). We have
$\unicode[STIX]{x1D6FD}$
(cf. [Reference Beilinson and DrinfeldBD91, §5.2.2]). We have
 $(E_{\tilde{x}},\unicode[STIX]{x1D6FD})\in \operatorname{Gr}_{x}(E_{\unicode[STIX]{x1D705}})$
and we need to show that
$(E_{\tilde{x}},\unicode[STIX]{x1D6FD})\in \operatorname{Gr}_{x}(E_{\unicode[STIX]{x1D705}})$
and we need to show that
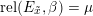 $\text{rel}(E_{\tilde{x}},\unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D707}$
. For simplicity, we will denote
$\text{rel}(E_{\tilde{x}},\unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D707}$
. For simplicity, we will denote
 ${\mathcal{P}}:=\operatorname{AJ}^{\mathscr{P},\unicode[STIX]{x1D706}}(\tilde{x})$
.
${\mathcal{P}}:=\operatorname{AJ}^{\mathscr{P},\unicode[STIX]{x1D706}}(\tilde{x})$
.
Let
![]() $\operatorname{Gr}_{J}$
(respectively
$\operatorname{Gr}_{J}$
(respectively
![]() $\operatorname{Gr}_{T}$
) be the global Grassmannian for the group scheme
$\operatorname{Gr}_{T}$
) be the global Grassmannian for the group scheme
![]() $J$
(respectively
$J$
(respectively
![]() $T$
). By [Reference YunYun11, Lemma 3.2.5], the morphism
$T$
). By [Reference YunYun11, Lemma 3.2.5], the morphism
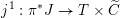 $j^{1}:\unicode[STIX]{x1D70B}^{\ast }J\rightarrow T\times \widetilde{C}$
induces a
$j^{1}:\unicode[STIX]{x1D70B}^{\ast }J\rightarrow T\times \widetilde{C}$
induces a
![]() $\text{W}$
-equivariant isomorphism
$\text{W}$
-equivariant isomorphism
 $$\begin{eqnarray}j_{\operatorname{Gr}}:\operatorname{Gr}_{J}\times _{(C\times B)}\widetilde{U}\simeq \operatorname{Gr}_{T}\times _{C}\widetilde{U}\end{eqnarray}$$
$$\begin{eqnarray}j_{\operatorname{Gr}}:\operatorname{Gr}_{J}\times _{(C\times B)}\widetilde{U}\simeq \operatorname{Gr}_{T}\times _{C}\widetilde{U}\end{eqnarray}$$
of group ind-schemes over
![]() $\widetilde{U}$
. We denote by
$\widetilde{U}$
. We denote by
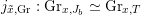 $j_{\tilde{x},\operatorname{Gr}}:\operatorname{Gr}_{x,J_{b}}\simeq \operatorname{Gr}_{x,T}$
the restriction of
$j_{\tilde{x},\operatorname{Gr}}:\operatorname{Gr}_{x,J_{b}}\simeq \operatorname{Gr}_{x,T}$
the restriction of
![]() $j_{\operatorname{Gr}}$
to
$j_{\operatorname{Gr}}$
to
![]() $\tilde{x}$
. We have
$\tilde{x}$
. We have
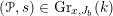 $({\mathcal{P}},s)\in \operatorname{Gr}_{x,J_{b}}(k)$
(here
$({\mathcal{P}},s)\in \operatorname{Gr}_{x,J_{b}}(k)$
(here
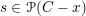 $s\in {\mathcal{P}}(C-x)$
is the canonical section) and one can check that
$s\in {\mathcal{P}}(C-x)$
is the canonical section) and one can check that
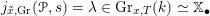 $j_{\tilde{x},\operatorname{Gr}}({\mathcal{P}},s)=\unicode[STIX]{x1D706}\in \operatorname{Gr}_{x,T}(k)\simeq \mathbb{X}_{\bullet }$
. The action of
$j_{\tilde{x},\operatorname{Gr}}({\mathcal{P}},s)=\unicode[STIX]{x1D706}\in \operatorname{Gr}_{x,T}(k)\simeq \mathbb{X}_{\bullet }$
. The action of
![]() $\operatorname{Gr}_{x,J_{b}}$
on
$\operatorname{Gr}_{x,J_{b}}$
on
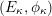 $(E_{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D705}})$
defines a map
$(E_{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D705}})$
defines a map
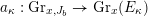 $a_{\unicode[STIX]{x1D705}}:\operatorname{Gr}_{x,J_{b}}\rightarrow \operatorname{Gr}_{x}(E_{\unicode[STIX]{x1D705}})$
. We claim that the following diagram is commutative
$a_{\unicode[STIX]{x1D705}}:\operatorname{Gr}_{x,J_{b}}\rightarrow \operatorname{Gr}_{x}(E_{\unicode[STIX]{x1D705}})$
. We claim that the following diagram is commutative

Assuming the claim we see that
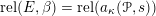 $\text{rel}(E,\unicode[STIX]{x1D6FD})=\text{rel}(a_{\unicode[STIX]{x1D705}}({\mathcal{P}},s))$
is equal to the image of
$\text{rel}(E,\unicode[STIX]{x1D6FD})=\text{rel}(a_{\unicode[STIX]{x1D705}}({\mathcal{P}},s))$
is equal to the image of
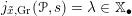 $j_{\tilde{x},\operatorname{Gr}}({\mathcal{P}},s)=\unicode[STIX]{x1D706}\in \mathbb{X}_{\bullet }$
in
$j_{\tilde{x},\operatorname{Gr}}({\mathcal{P}},s)=\unicode[STIX]{x1D706}\in \mathbb{X}_{\bullet }$
in
![]() $\mathbb{X}_{\bullet }/\text{W}$
. But by assumption
$\mathbb{X}_{\bullet }/\text{W}$
. But by assumption
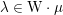 $\unicode[STIX]{x1D706}\in \text{W}\cdot \unicode[STIX]{x1D707}$
. This finishes the proof of Lemma 4.4.1.
$\unicode[STIX]{x1D706}\in \text{W}\cdot \unicode[STIX]{x1D707}$
. This finishes the proof of Lemma 4.4.1.
To prove the claim, recall that a trivialization
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D705}}$
of
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D705}}$
of
![]() $E_{\unicode[STIX]{x1D705}}$
on
$E_{\unicode[STIX]{x1D705}}$
on
![]() $\operatorname{Spec}{\mathcal{O}}_{x}$
defines an isomorphism
$\operatorname{Spec}{\mathcal{O}}_{x}$
defines an isomorphism
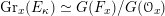 $\operatorname{Gr}_{x}(E_{\unicode[STIX]{x1D705}})\simeq G(F_{x})/G({\mathcal{O}}_{x})$
. Moreover, under the canonical isomorphism
$\operatorname{Gr}_{x}(E_{\unicode[STIX]{x1D705}})\simeq G(F_{x})/G({\mathcal{O}}_{x})$
. Moreover, under the canonical isomorphism
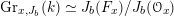 $\operatorname{Gr}_{x,J_{b}}(k)\simeq J_{b}(F_{x})/J_{b}({\mathcal{O}}_{x})$
,
$\operatorname{Gr}_{x,J_{b}}(k)\simeq J_{b}(F_{x})/J_{b}({\mathcal{O}}_{x})$
,
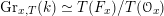 $\operatorname{Gr}_{x,T}(k)\simeq T(F_{x})/T({\mathcal{O}}_{x})$
and
$\operatorname{Gr}_{x,T}(k)\simeq T(F_{x})/T({\mathcal{O}}_{x})$
and
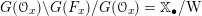 $G({\mathcal{O}}_{x})\backslash G(F_{x})/G({\mathcal{O}}_{x})=\mathbb{X}_{\bullet }/\text{W}$
, the diagram (4.4.2) can be identified with
$G({\mathcal{O}}_{x})\backslash G(F_{x})/G({\mathcal{O}}_{x})=\mathbb{X}_{\bullet }/\text{W}$
, the diagram (4.4.2) can be identified with

where the upper arrow is induced by the homomorphism
 $$\begin{eqnarray}J_{b}\stackrel{a_{E_{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D705}}}}{\simeq }\operatorname{Aut}(E_{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D705}})\rightarrow \operatorname{Aut}(E_{\unicode[STIX]{x1D705}})\stackrel{\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D705}}}{\simeq }G\end{eqnarray}$$
$$\begin{eqnarray}J_{b}\stackrel{a_{E_{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D705}}}}{\simeq }\operatorname{Aut}(E_{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D705}})\rightarrow \operatorname{Aut}(E_{\unicode[STIX]{x1D705}})\stackrel{\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D705}}}{\simeq }G\end{eqnarray}$$
and the arrow in the left column is induced by the homomorphism
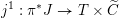 $j^{1}:\unicode[STIX]{x1D70B}^{\ast }J\rightarrow T\times \widetilde{C}$
. Let
$j^{1}:\unicode[STIX]{x1D70B}^{\ast }J\rightarrow T\times \widetilde{C}$
. Let
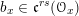 $b_{x}\in \mathfrak{c}^{rs}({\mathcal{O}}_{x})$
be the restriction of
$b_{x}\in \mathfrak{c}^{rs}({\mathcal{O}}_{x})$
be the restriction of
![]() $b$
to
$b$
to
![]() $\operatorname{Spec}{\mathcal{O}}_{x}$
. Using the definition of
$\operatorname{Spec}{\mathcal{O}}_{x}$
. Using the definition of
![]() $a_{E_{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D705}}}$
in (2.6.1), it is not hard to see that the restriction of (4.4.3) to
$a_{E_{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D705}}}$
in (2.6.1), it is not hard to see that the restriction of (4.4.3) to
![]() $\operatorname{Spec}{\mathcal{O}}_{x}$
is equal to
$\operatorname{Spec}{\mathcal{O}}_{x}$
is equal to
 $$\begin{eqnarray}J_{b_{x}}\simeq I_{\text{kos}(b_{x})}{\hookrightarrow}G\times \operatorname{Spec}{\mathcal{O}}_{x},\end{eqnarray}$$
$$\begin{eqnarray}J_{b_{x}}\simeq I_{\text{kos}(b_{x})}{\hookrightarrow}G\times \operatorname{Spec}{\mathcal{O}}_{x},\end{eqnarray}$$
up to conjugation by an element in
![]() $G({\mathcal{O}}_{x})$
. Here
$G({\mathcal{O}}_{x})$
. Here
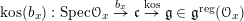 $\text{kos}(b_{x}):\operatorname{Spec}{\mathcal{O}}_{x}\stackrel{b_{x}}{\rightarrow }\mathfrak{c}\stackrel{\text{kos}}{\rightarrow }\mathfrak{g}\in \mathfrak{g}^{\text{reg}}({\mathcal{O}}_{x})$
and the first isomorphism is induced by the canonical isomorphism
$\text{kos}(b_{x}):\operatorname{Spec}{\mathcal{O}}_{x}\stackrel{b_{x}}{\rightarrow }\mathfrak{c}\stackrel{\text{kos}}{\rightarrow }\mathfrak{g}\in \mathfrak{g}^{\text{reg}}({\mathcal{O}}_{x})$
and the first isomorphism is induced by the canonical isomorphism
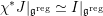 $\unicode[STIX]{x1D712}^{\ast }J|_{\mathfrak{g}^{\text{reg}}}\simeq I|_{\mathfrak{g}^{\text{reg}}}$
in Proposition 2.5.1. Therefore, to prove the claim, it is enough to show that the restrictionFootnote
7
of
$\unicode[STIX]{x1D712}^{\ast }J|_{\mathfrak{g}^{\text{reg}}}\simeq I|_{\mathfrak{g}^{\text{reg}}}$
in Proposition 2.5.1. Therefore, to prove the claim, it is enough to show that the restrictionFootnote
7
of
![]() $j^{1}$
to
$j^{1}$
to
![]() $\operatorname{Spec}{\mathcal{O}}_{x}$
is equal to the map (4.4.4) up to left and right multiplication by elements in
$\operatorname{Spec}{\mathcal{O}}_{x}$
is equal to the map (4.4.4) up to left and right multiplication by elements in
![]() $G({\mathcal{O}}_{x})$
. To see this, we first observe that the point
$G({\mathcal{O}}_{x})$
. To see this, we first observe that the point
![]() $\tilde{x}$
defines a lifting
$\tilde{x}$
defines a lifting
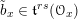 $\tilde{b}_{x}\in \mathfrak{t}^{rs}({\mathcal{O}}_{x})$
of
$\tilde{b}_{x}\in \mathfrak{t}^{rs}({\mathcal{O}}_{x})$
of
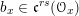 $b_{x}\in \mathfrak{c}^{rs}({\mathcal{O}}_{x})$
. Since the map
$b_{x}\in \mathfrak{c}^{rs}({\mathcal{O}}_{x})$
. Since the map
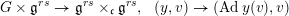 $G\times \mathfrak{g}^{rs}\rightarrow \mathfrak{g}^{rs}\times _{\mathfrak{c}}\mathfrak{g}^{rs},~~(y,v)\rightarrow (\operatorname{Ad}y(v),v)$
is smooth, there exists
$G\times \mathfrak{g}^{rs}\rightarrow \mathfrak{g}^{rs}\times _{\mathfrak{c}}\mathfrak{g}^{rs},~~(y,v)\rightarrow (\operatorname{Ad}y(v),v)$
is smooth, there exists
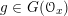 $g\in G({\mathcal{O}}_{x})$
such that
$g\in G({\mathcal{O}}_{x})$
such that
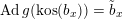 $\operatorname{Ad}g(\text{kos}(b_{x}))=\tilde{b}_{x}$
. The map
$\operatorname{Ad}g(\text{kos}(b_{x}))=\tilde{b}_{x}$
. The map
![]() $\operatorname{Ad}g$
induced an isomorphism
$\operatorname{Ad}g$
induced an isomorphism
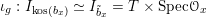 $\unicode[STIX]{x1D704}_{g}:I_{\text{kos}(b_{x})}\simeq I_{\tilde{b}_{x}}=T\times \operatorname{Spec}{\mathcal{O}}_{x}$
, which is independent of the choice of
$\unicode[STIX]{x1D704}_{g}:I_{\text{kos}(b_{x})}\simeq I_{\tilde{b}_{x}}=T\times \operatorname{Spec}{\mathcal{O}}_{x}$
, which is independent of the choice of
![]() $g$
, and according to [Reference NgôNgô10, Proposition 2.4.2] the restriction of
$g$
, and according to [Reference NgôNgô10, Proposition 2.4.2] the restriction of
![]() $j^{1}$
to
$j^{1}$
to
![]() $\operatorname{Spec}{\mathcal{O}}_{x}$
is given by
$\operatorname{Spec}{\mathcal{O}}_{x}$
is given by
 $$\begin{eqnarray}J_{b_{x}}\simeq I_{\text{kos}(b_{x})}\stackrel{\unicode[STIX]{x1D704}_{g}}{\simeq }T\times \operatorname{Spec}{\mathcal{O}}_{x},\end{eqnarray}$$
$$\begin{eqnarray}J_{b_{x}}\simeq I_{\text{kos}(b_{x})}\stackrel{\unicode[STIX]{x1D704}_{g}}{\simeq }T\times \operatorname{Spec}{\mathcal{O}}_{x},\end{eqnarray}$$
where the first map is the canonical isomorphism mentioned before. The above description implies the map (4.4.4) is equal to the map (4.4.5) up to left and right multiplication by elements in
![]() $G({\mathcal{O}}_{x})$
. This finishes the proof of the claim.
$G({\mathcal{O}}_{x})$
. This finishes the proof of the claim.
5 Main result
We assume that
![]() $G$
is semi-simple over
$G$
is semi-simple over
![]() $k$
whose characteristic
$k$
whose characteristic
![]() $p$
is positive and does not divide the order of the Weyl group of
$p$
is positive and does not divide the order of the Weyl group of
![]() $G$
. Let
$G$
. Let
![]() $C$
be a smooth projective curve over
$C$
be a smooth projective curve over
![]() $k$
, of genus at least two. In this case,
$k$
, of genus at least two. In this case,
![]() $\operatorname{Bun}_{G}$
is a ‘good’ stack in the sense of [Reference Beilinson and DrinfeldBD91, §1.1.1] (see also §B.5). Let
$\operatorname{Bun}_{G}$
is a ‘good’ stack in the sense of [Reference Beilinson and DrinfeldBD91, §1.1.1] (see also §B.5). Let
![]() $D_{\operatorname{Bun}_{G}}$
be the sheaf of algebras on
$D_{\operatorname{Bun}_{G}}$
be the sheaf of algebras on
![]() $\operatorname{Higgs}_{G}^{\prime }$
in Proposition B.5.1. Denote by
$\operatorname{Higgs}_{G}^{\prime }$
in Proposition B.5.1. Denote by
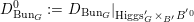 $D_{\operatorname{Bun}_{G}}^{0}:=D_{\operatorname{Bun}_{G}}|_{\operatorname{Higgs}_{G}^{\prime }\times _{B^{\prime }}B^{^{\prime }0}}$
the restriction of
$D_{\operatorname{Bun}_{G}}^{0}:=D_{\operatorname{Bun}_{G}}|_{\operatorname{Higgs}_{G}^{\prime }\times _{B^{\prime }}B^{^{\prime }0}}$
the restriction of
![]() $D_{\operatorname{Bun}_{G}}$
to the smooth part of the Hitchin fibration. We define
$D_{\operatorname{Bun}_{G}}$
to the smooth part of the Hitchin fibration. We define
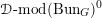 ${\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})^{0}$
as the category of
${\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})^{0}$
as the category of
![]() $D_{\operatorname{Bun}_{G}}^{0}$
-modules. As explained in §B.5, the category
$D_{\operatorname{Bun}_{G}}^{0}$
-modules. As explained in §B.5, the category
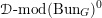 ${\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})^{0}$
is a localization of the category of
${\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})^{0}$
is a localization of the category of
![]() ${\mathcal{D}}$
-modules on
${\mathcal{D}}$
-modules on
![]() $\operatorname{Bun}_{G}$
and is canonical equivalent to the category of twisted sheaves
$\operatorname{Bun}_{G}$
and is canonical equivalent to the category of twisted sheaves
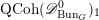 $\operatorname{QCoh}(\mathscr{D}_{\operatorname{Bun}_{G}}^{0})_{1}$
, where
$\operatorname{QCoh}(\mathscr{D}_{\operatorname{Bun}_{G}}^{0})_{1}$
, where
 $\mathscr{D}_{\operatorname{Bun}_{G}}^{0}=\mathscr{D}_{\operatorname{Bun}_{G}}\times _{B^{\prime }}B^{^{\prime }0}$
and
$\mathscr{D}_{\operatorname{Bun}_{G}}^{0}=\mathscr{D}_{\operatorname{Bun}_{G}}\times _{B^{\prime }}B^{^{\prime }0}$
and
![]() $\mathscr{D}_{\operatorname{Bun}_{G}}$
is the gerbe of crystalline differential operators on
$\mathscr{D}_{\operatorname{Bun}_{G}}$
is the gerbe of crystalline differential operators on
![]() $\operatorname{Higgs}_{G}^{\prime }$
. On the dual side, let
$\operatorname{Higgs}_{G}^{\prime }$
. On the dual side, let
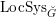 $\operatorname{LocSys}_{\breve{G}}$
be the stack of de Rham
$\operatorname{LocSys}_{\breve{G}}$
be the stack of de Rham
![]() $\breve{G}$
-local systems on
$\breve{G}$
-local systems on
![]() $C$
. Recall that in [Reference Chen and ZhuCZ15], we constructed a fibration
$C$
. Recall that in [Reference Chen and ZhuCZ15], we constructed a fibration
 $$\begin{eqnarray}h_{p}:\operatorname{LocSys}_{\breve{G}}\rightarrow B^{\prime }\end{eqnarray}$$
$$\begin{eqnarray}h_{p}:\operatorname{LocSys}_{\breve{G}}\rightarrow B^{\prime }\end{eqnarray}$$
from
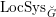 $\operatorname{LocSys}_{\breve{G}}$
to the Hitchin base
$\operatorname{LocSys}_{\breve{G}}$
to the Hitchin base
![]() $B^{\prime }$
, which can be regraded as a deformation of the usual Hitchin fibration. We define
$B^{\prime }$
, which can be regraded as a deformation of the usual Hitchin fibration. We define
 $$\begin{eqnarray}\operatorname{LocSys}_{\breve{G}}^{0}:=\operatorname{LocSys}_{\breve{G}}\times _{B^{\prime }}B^{^{\prime }0}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{LocSys}_{\breve{G}}^{0}:=\operatorname{LocSys}_{\breve{G}}\times _{B^{\prime }}B^{^{\prime }0}.\end{eqnarray}$$
Our goal is to prove the following theorem.
Theorem 5.0.1. Assume
![]() $G$
is semi-simple and the genus of
$G$
is semi-simple and the genus of
![]() $C$
is at least two. For a choice of a square root
$C$
is at least two. For a choice of a square root
![]() $\unicode[STIX]{x1D705}$
of
$\unicode[STIX]{x1D705}$
of
![]() $\unicode[STIX]{x1D714}_{C}$
, we have a canonical equivalence of bounded derived categories
$\unicode[STIX]{x1D714}_{C}$
, we have a canonical equivalence of bounded derived categories
 $$\begin{eqnarray}\mathfrak{D}_{\unicode[STIX]{x1D705}}:D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})^{0})\simeq D^{b}(\operatorname{QCoh}(\operatorname{LocSys}_{\breve{G}}^{0})).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{D}_{\unicode[STIX]{x1D705}}:D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})^{0})\simeq D^{b}(\operatorname{QCoh}(\operatorname{LocSys}_{\breve{G}}^{0})).\end{eqnarray}$$
The proof of above theorem is divided into two steps. The first step, which involves the Langlands duality, is to establish a twisted version of the classical duality (see §5.2). The second step, which does not involve the Langlands duality, is to establish two abelianization theorems (see §5.3) for which we need a choice of square root
![]() $\unicode[STIX]{x1D705}$
of
$\unicode[STIX]{x1D705}$
of
![]() $\unicode[STIX]{x1D714}_{C}$
. Combining above two steps, our main theorem follows from a general version of the Fourier–Mukai transform (see §5.4).
$\unicode[STIX]{x1D714}_{C}$
. Combining above two steps, our main theorem follows from a general version of the Fourier–Mukai transform (see §5.4).
5.1 The
 $\breve{\mathscr{P}}^{\prime }$
-torsor
$\breve{\mathscr{P}}^{\prime }$
-torsor
 $\breve{\mathscr{H}}$
$\breve{\mathscr{H}}$
We first recall that in [Reference Chen and ZhuCZ15], we constructed a
![]() $\breve{\mathscr{P}}^{\prime }$
-torsor
$\breve{\mathscr{P}}^{\prime }$
-torsor
![]() $\breve{\mathscr{H}}$
. It is defined via the following Cartesian diagram.
$\breve{\mathscr{H}}$
. It is defined via the following Cartesian diagram.

Here
![]() $\breve{J}^{p}$
is the pullback of the universal centralizer
$\breve{J}^{p}$
is the pullback of the universal centralizer
![]() $\breve{J}^{\prime }$
over
$\breve{J}^{\prime }$
over
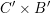 $C^{\prime }\times B^{\prime }$
along the relative Frobenius map
$C^{\prime }\times B^{\prime }$
along the relative Frobenius map
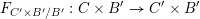 $F_{C^{\prime }\times B^{\prime }/B^{\prime }}:C\times B^{\prime }\rightarrow C^{\prime }\times B^{\prime }$
. This is a group scheme with a canonical connection along
$F_{C^{\prime }\times B^{\prime }/B^{\prime }}:C\times B^{\prime }\rightarrow C^{\prime }\times B^{\prime }$
. This is a group scheme with a canonical connection along
![]() $C$
, and therefore it makes sense to talk about the stack
$C$
, and therefore it makes sense to talk about the stack
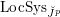 $\operatorname{LocSys}_{\breve{J}^{p}}$
of
$\operatorname{LocSys}_{\breve{J}^{p}}$
of
![]() $\breve{J}^{p}$
-torsors with flat connections. In addition, it admits a map
$\breve{J}^{p}$
-torsors with flat connections. In addition, it admits a map
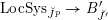 $\operatorname{LocSys}_{\breve{J}^{p}}\rightarrow B_{\breve{J}^{\prime }}^{\prime }$
. We refer to [Reference Chen and ZhuCZ15, Appendix] for generalities.
$\operatorname{LocSys}_{\breve{J}^{p}}\rightarrow B_{\breve{J}^{\prime }}^{\prime }$
. We refer to [Reference Chen and ZhuCZ15, Appendix] for generalities.
Recall that there is a description of
![]() $\mathscr{P}$
in terms of
$\mathscr{P}$
in terms of
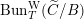 $\operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B)$
. We give a similar description of the
$\operatorname{Bun}_{T}^{\text{W}}(\widetilde{C}/B)$
. We give a similar description of the
![]() $\breve{\mathscr{P}}^{\prime }$
-torsor
$\breve{\mathscr{P}}^{\prime }$
-torsor
![]() $\breve{\mathscr{H}}$
in terms of a
$\breve{\mathscr{H}}$
in terms of a
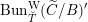 $\operatorname{Bun}_{\breve{T}}^{\text{W}}(\widetilde{C}/B)^{\prime }$
-torsor. Recall that
$\operatorname{Bun}_{\breve{T}}^{\text{W}}(\widetilde{C}/B)^{\prime }$
-torsor. Recall that
![]() $\breve{\unicode[STIX]{x1D70F}}^{\prime }$
is regarded as a section of
$\breve{\unicode[STIX]{x1D70F}}^{\prime }$
is regarded as a section of
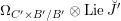 $\unicode[STIX]{x1D6FA}_{C^{\prime }\times B^{\prime }/B^{\prime }}\otimes \operatorname{Lie}\,\breve{J}^{\prime }$
, which defines a
$\unicode[STIX]{x1D6FA}_{C^{\prime }\times B^{\prime }/B^{\prime }}\otimes \operatorname{Lie}\,\breve{J}^{\prime }$
, which defines a
![]() $\breve{J}^{\prime }$
-gerbe
$\breve{J}^{\prime }$
-gerbe
![]() $\mathscr{D}(\breve{\unicode[STIX]{x1D70F}}^{\prime })$
on
$\mathscr{D}(\breve{\unicode[STIX]{x1D70F}}^{\prime })$
on
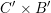 $C^{\prime }\times B^{\prime }$
(see §B.4) and according to [Reference Chen and ZhuCZ15, Proposition A.9],
$C^{\prime }\times B^{\prime }$
(see §B.4) and according to [Reference Chen and ZhuCZ15, Proposition A.9],
![]() $\breve{\mathscr{H}}$
is isomorphic to
$\breve{\mathscr{H}}$
is isomorphic to
![]() $\mathscr{T}_{\mathscr{D}(\breve{\unicode[STIX]{x1D70F}}^{\prime })}$
, the stack of splittings of
$\mathscr{T}_{\mathscr{D}(\breve{\unicode[STIX]{x1D70F}}^{\prime })}$
, the stack of splittings of
![]() $\mathscr{D}(\breve{\unicode[STIX]{x1D70F}}^{\prime })$
over
$\mathscr{D}(\breve{\unicode[STIX]{x1D70F}}^{\prime })$
over
![]() $B^{\prime }$
. Therefore by Lemma 3.2.1 we have
$B^{\prime }$
. Therefore by Lemma 3.2.1 we have
 $$\begin{eqnarray}\breve{\mathscr{H}}|_{B^{^{\prime }0}}\simeq \mathscr{T}_{\mathscr{D}(\breve{\unicode[STIX]{x1D70F}}^{\prime })_{\breve{T}}}^{\text{W},+}|_{B^{^{\prime }0}},\end{eqnarray}$$
$$\begin{eqnarray}\breve{\mathscr{H}}|_{B^{^{\prime }0}}\simeq \mathscr{T}_{\mathscr{D}(\breve{\unicode[STIX]{x1D70F}}^{\prime })_{\breve{T}}}^{\text{W},+}|_{B^{^{\prime }0}},\end{eqnarray}$$
where
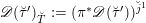 $\mathscr{D}(\breve{\unicode[STIX]{x1D70F}}^{\prime })_{\breve{T}}:=(\unicode[STIX]{x1D70B}^{\ast }\mathscr{D}(\breve{\unicode[STIX]{x1D70F}}^{\prime }))^{\breve{j}^{1}}$
is the
$\mathscr{D}(\breve{\unicode[STIX]{x1D70F}}^{\prime })_{\breve{T}}:=(\unicode[STIX]{x1D70B}^{\ast }\mathscr{D}(\breve{\unicode[STIX]{x1D70F}}^{\prime }))^{\breve{j}^{1}}$
is the
![]() $\breve{T}$
-gerbe on
$\breve{T}$
-gerbe on
![]() $\widetilde{C}^{\prime }$
induced from
$\widetilde{C}^{\prime }$
induced from
![]() $\mathscr{D}(\breve{\unicode[STIX]{x1D70F}}^{\prime })$
using maps
$\mathscr{D}(\breve{\unicode[STIX]{x1D70F}}^{\prime })$
using maps
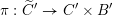 $\unicode[STIX]{x1D70B}:\widetilde{C}^{\prime }\rightarrow C^{\prime }\times B^{\prime }$
and
$\unicode[STIX]{x1D70B}:\widetilde{C}^{\prime }\rightarrow C^{\prime }\times B^{\prime }$
and
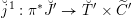 $\breve{j}^{1}:\unicode[STIX]{x1D70B}^{\ast }\breve{J}^{\prime }\rightarrow \breve{T}^{\prime }\times \widetilde{C}^{\prime }$
(see §A.6 for the induction functor of gerbes).
$\breve{j}^{1}:\unicode[STIX]{x1D70B}^{\ast }\breve{J}^{\prime }\rightarrow \breve{T}^{\prime }\times \widetilde{C}^{\prime }$
(see §A.6 for the induction functor of gerbes).
On the other hand, using the definition of
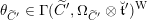 $\unicode[STIX]{x1D703}_{\widetilde{C}^{\prime }}\in \unicode[STIX]{x1D6E4}(\widetilde{C}^{\prime },\unicode[STIX]{x1D6FA}_{\widetilde{C}^{\prime }}\otimes \breve{\mathfrak{t}}^{\prime })^{\text{W}}$
in §4.1 one can check that
$\unicode[STIX]{x1D703}_{\widetilde{C}^{\prime }}\in \unicode[STIX]{x1D6E4}(\widetilde{C}^{\prime },\unicode[STIX]{x1D6FA}_{\widetilde{C}^{\prime }}\otimes \breve{\mathfrak{t}}^{\prime })^{\text{W}}$
in §4.1 one can check that
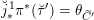 $\breve{j}_{\ast }^{1}\unicode[STIX]{x1D70B}^{\ast }(\breve{\unicode[STIX]{x1D70F}}^{\prime })=\unicode[STIX]{x1D703}_{\widetilde{C}^{\prime }}$
, where
$\breve{j}_{\ast }^{1}\unicode[STIX]{x1D70B}^{\ast }(\breve{\unicode[STIX]{x1D70F}}^{\prime })=\unicode[STIX]{x1D703}_{\widetilde{C}^{\prime }}$
, where
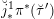 $\breve{j}_{\ast }^{1}\unicode[STIX]{x1D70B}^{\ast }(\breve{\unicode[STIX]{x1D70F}}^{\prime })$
is the
$\breve{j}_{\ast }^{1}\unicode[STIX]{x1D70B}^{\ast }(\breve{\unicode[STIX]{x1D70F}}^{\prime })$
is the
![]() $\breve{\mathfrak{t}}^{\prime }$
-valued 1-form induced from
$\breve{\mathfrak{t}}^{\prime }$
-valued 1-form induced from
![]() $\breve{\unicode[STIX]{x1D70F}}^{\prime }$
using maps
$\breve{\unicode[STIX]{x1D70F}}^{\prime }$
using maps
![]() $\unicode[STIX]{x1D70B}$
and
$\unicode[STIX]{x1D70B}$
and
![]() $\breve{j}^{1}$
. Therefore, by Lemma B.4.1 we see that over
$\breve{j}^{1}$
. Therefore, by Lemma B.4.1 we see that over
![]() $B^{^{\prime }0}$
we have
$B^{^{\prime }0}$
we have
 $$\begin{eqnarray}\mathscr{D}(\breve{\unicode[STIX]{x1D70F}}^{\prime })_{\breve{T}}:=(\unicode[STIX]{x1D70B}^{\ast }\mathscr{D}(\breve{\unicode[STIX]{x1D70F}}^{\prime }))^{\breve{j}^{1}}\simeq \mathscr{D}(\breve{j}_{\ast }^{1}\unicode[STIX]{x1D70B}^{\ast }(\breve{\unicode[STIX]{x1D70F}}^{\prime }))\simeq \mathscr{D}(\unicode[STIX]{x1D703}_{\widetilde{C}^{\prime }}).\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{D}(\breve{\unicode[STIX]{x1D70F}}^{\prime })_{\breve{T}}:=(\unicode[STIX]{x1D70B}^{\ast }\mathscr{D}(\breve{\unicode[STIX]{x1D70F}}^{\prime }))^{\breve{j}^{1}}\simeq \mathscr{D}(\breve{j}_{\ast }^{1}\unicode[STIX]{x1D70B}^{\ast }(\breve{\unicode[STIX]{x1D70F}}^{\prime }))\simeq \mathscr{D}(\unicode[STIX]{x1D703}_{\widetilde{C}^{\prime }}).\end{eqnarray}$$
Hence combining (5.1.2) and (5.1.3) we get the following Galois description of
![]() $\breve{\mathscr{H}}$
.
$\breve{\mathscr{H}}$
.
Corollary 5.1.1. There is a canonical isomorphism of
![]() $\breve{\mathscr{P}}^{\prime }$
-torsors
$\breve{\mathscr{P}}^{\prime }$
-torsors
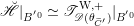 $\breve{\mathscr{H}}|_{B^{^{\prime }0}}\simeq \mathscr{T}_{\mathscr{D}(\unicode[STIX]{x1D703}_{\widetilde{C}^{\prime }})}^{\text{W},+}|_{B^{^{\prime }0}}$
.
$\breve{\mathscr{H}}|_{B^{^{\prime }0}}\simeq \mathscr{T}_{\mathscr{D}(\unicode[STIX]{x1D703}_{\widetilde{C}^{\prime }})}^{\text{W},+}|_{B^{^{\prime }0}}$
.
5.2 Twisted duality
Let us construct the twisted duality. Let
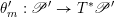 $\unicode[STIX]{x1D703}_{m}^{\prime }:\mathscr{P}^{\prime }\rightarrow T^{\ast }\mathscr{P}^{\prime }$
denote the canonical multiplicative one form constructed in §4.2. Let
$\unicode[STIX]{x1D703}_{m}^{\prime }:\mathscr{P}^{\prime }\rightarrow T^{\ast }\mathscr{P}^{\prime }$
denote the canonical multiplicative one form constructed in §4.2. Let
![]() $\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })$
denote the corresponding
$\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })$
denote the corresponding
![]() $\mathbb{G}_{m}$
-gerbe on
$\mathbb{G}_{m}$
-gerbe on
![]() $\mathscr{P}^{\prime }$
obtained by pullback of
$\mathscr{P}^{\prime }$
obtained by pullback of
![]() $\mathscr{D}_{\mathscr{P}}$
on
$\mathscr{D}_{\mathscr{P}}$
on
![]() $T^{\ast }\mathscr{P}^{\prime }$
by
$T^{\ast }\mathscr{P}^{\prime }$
by
![]() $\unicode[STIX]{x1D703}_{m}^{\prime }$
(see §B.4). According to §C.2, the gerbe
$\unicode[STIX]{x1D703}_{m}^{\prime }$
(see §B.4). According to §C.2, the gerbe
![]() $\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })$
is canonically multiplicative. Moreover, according to §A.7, the stack of multiplicative splittings of
$\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })$
is canonically multiplicative. Moreover, according to §A.7, the stack of multiplicative splittings of
![]() $\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })$
over
$\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })$
over
![]() $B^{\prime }$
is a
$B^{\prime }$
is a
![]() $(\mathscr{P}^{\prime })^{\vee }$
-torsor
$(\mathscr{P}^{\prime })^{\vee }$
-torsor
![]() $\mathscr{T}_{\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })}$
. Our goal is to prove the following theorem.
$\mathscr{T}_{\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })}$
. Our goal is to prove the following theorem.
Theorem 5.2.1. There is a canonical isomorphism of
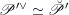 ${\mathscr{P}^{\prime }}^{\vee }\simeq \breve{\mathscr{P}}^{\prime }$
-torsors
${\mathscr{P}^{\prime }}^{\vee }\simeq \breve{\mathscr{P}}^{\prime }$
-torsors
 $$\begin{eqnarray}\mathfrak{D}:\mathscr{T}_{\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })}|_{B^{^{\prime }0}}\simeq \breve{\mathscr{H}}|_{B^{^{\prime }0}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{D}:\mathscr{T}_{\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })}|_{B^{^{\prime }0}}\simeq \breve{\mathscr{H}}|_{B^{^{\prime }0}}.\end{eqnarray}$$
For the rest of this subsection we will restrict everything to
![]() $B^{^{\prime }0}$
. Recall the Abel–Jacobi map
$B^{^{\prime }0}$
. Recall the Abel–Jacobi map
 $\operatorname{AJ}^{\mathscr{P}^{\prime }}:\widetilde{C}^{\prime }\times \mathbb{X}_{\bullet }\rightarrow \mathscr{P}^{\prime }$
. By Proposition 4.2.1 we have
$\operatorname{AJ}^{\mathscr{P}^{\prime }}:\widetilde{C}^{\prime }\times \mathbb{X}_{\bullet }\rightarrow \mathscr{P}^{\prime }$
. By Proposition 4.2.1 we have
 $(\operatorname{AJ}^{\mathscr{P}^{\prime }})^{\ast }\unicode[STIX]{x1D703}_{m}^{\prime }=\unicode[STIX]{x1D703}_{\widetilde{C}^{\prime }}$
. Therefore, Lemma B.4.1 implies that
$(\operatorname{AJ}^{\mathscr{P}^{\prime }})^{\ast }\unicode[STIX]{x1D703}_{m}^{\prime }=\unicode[STIX]{x1D703}_{\widetilde{C}^{\prime }}$
. Therefore, Lemma B.4.1 implies that
 $$\begin{eqnarray}(\operatorname{AJ}^{\mathscr{P}^{\prime }})^{\ast }\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })=\mathscr{D}(\unicode[STIX]{x1D703}_{\widetilde{C}^{\prime }}).\end{eqnarray}$$
$$\begin{eqnarray}(\operatorname{AJ}^{\mathscr{P}^{\prime }})^{\ast }\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })=\mathscr{D}(\unicode[STIX]{x1D703}_{\widetilde{C}^{\prime }}).\end{eqnarray}$$
Since the Abel–Jacobi map
![]() $\operatorname{AJ}^{\mathscr{P}^{\prime }}$
is
$\operatorname{AJ}^{\mathscr{P}^{\prime }}$
is
![]() $\text{W}$
-equivariant, pullback via
$\text{W}$
-equivariant, pullback via
![]() $\operatorname{AJ}^{\mathscr{P}^{\prime }}$
defines a functor
$\operatorname{AJ}^{\mathscr{P}^{\prime }}$
defines a functor
 $$\begin{eqnarray}\tilde{\mathfrak{D}}:\mathscr{T}_{\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })}\rightarrow \mathscr{T}_{\mathscr{D}(\unicode[STIX]{x1D703}_{\widetilde{C}^{\prime }})}^{\text{W}}.\end{eqnarray}$$
$$\begin{eqnarray}\tilde{\mathfrak{D}}:\mathscr{T}_{\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })}\rightarrow \mathscr{T}_{\mathscr{D}(\unicode[STIX]{x1D703}_{\widetilde{C}^{\prime }})}^{\text{W}}.\end{eqnarray}$$
We claim that
![]() $\tilde{\mathfrak{D}}$
canonically lifts to a morphism
$\tilde{\mathfrak{D}}$
canonically lifts to a morphism
 $$\begin{eqnarray}\mathfrak{D}:\mathscr{T}_{\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })}\rightarrow \mathscr{T}_{\mathscr{D}(\unicode[STIX]{x1D703}_{\widetilde{C}^{\prime }})}^{\text{W},+}\simeq \breve{\mathscr{H}},\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{D}:\mathscr{T}_{\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })}\rightarrow \mathscr{T}_{\mathscr{D}(\unicode[STIX]{x1D703}_{\widetilde{C}^{\prime }})}^{\text{W},+}\simeq \breve{\mathscr{H}},\end{eqnarray}$$
where the second isomorphism is Corollary 5.1.1. Let
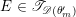 $E\in \mathscr{T}_{\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })}$
be a tensor splitting of
$E\in \mathscr{T}_{\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })}$
be a tensor splitting of
![]() $\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })$
. We need to show that the splitting
$\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })$
. We need to show that the splitting
 $$\begin{eqnarray}(\tilde{\mathfrak{D}}(E))^{\unicode[STIX]{x1D6FC}}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}^{\prime }}=(\operatorname{AJ}^{\mathscr{P}^{\prime }})^{\ast }E|_{(\widetilde{C}_{\unicode[STIX]{x1D6FC}}^{\prime },\breve{\unicode[STIX]{x1D6FC}})}\end{eqnarray}$$
$$\begin{eqnarray}(\tilde{\mathfrak{D}}(E))^{\unicode[STIX]{x1D6FC}}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}^{\prime }}=(\operatorname{AJ}^{\mathscr{P}^{\prime }})^{\ast }E|_{(\widetilde{C}_{\unicode[STIX]{x1D6FC}}^{\prime },\breve{\unicode[STIX]{x1D6FC}})}\end{eqnarray}$$
admits a canonical isomorphism compatible with the canonical splitting
![]() $E_{\unicode[STIX]{x1D6FC}}^{0}$
of
$E_{\unicode[STIX]{x1D6FC}}^{0}$
of
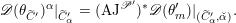 $\mathscr{D}(\unicode[STIX]{x1D703}_{\widetilde{C}^{\prime }})^{\unicode[STIX]{x1D6FC}}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}^{\prime }}=(\operatorname{AJ}^{\mathscr{P}^{\prime }})^{\ast }\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })|_{(\widetilde{C}_{\unicode[STIX]{x1D6FC}}^{\prime },\breve{\unicode[STIX]{x1D6FC}})}.$
However, this follows from the fact that
$\mathscr{D}(\unicode[STIX]{x1D703}_{\widetilde{C}^{\prime }})^{\unicode[STIX]{x1D6FC}}|_{\widetilde{C}_{\unicode[STIX]{x1D6FC}}^{\prime }}=(\operatorname{AJ}^{\mathscr{P}^{\prime }})^{\ast }\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })|_{(\widetilde{C}_{\unicode[STIX]{x1D6FC}}^{\prime },\breve{\unicode[STIX]{x1D6FC}})}.$
However, this follows from the fact that
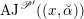 $\operatorname{AJ}^{\mathscr{P}^{\prime }}((x,\breve{\unicode[STIX]{x1D6FC}}))$
is the unit of
$\operatorname{AJ}^{\mathscr{P}^{\prime }}((x,\breve{\unicode[STIX]{x1D6FC}}))$
is the unit of
![]() $\mathscr{P}^{\prime }$
for
$\mathscr{P}^{\prime }$
for
![]() $x\in \widetilde{C}_{\unicode[STIX]{x1D6FC}}^{\prime }$
and a tensor splitting
$x\in \widetilde{C}_{\unicode[STIX]{x1D6FC}}^{\prime }$
and a tensor splitting
![]() $E$
of a multiplicative
$E$
of a multiplicative
![]() $\mathbb{G}_{m}$
-gerbe
$\mathbb{G}_{m}$
-gerbe
![]() $\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })$
is canonically isomorphic to the canonical splitting
$\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })$
is canonically isomorphic to the canonical splitting
![]() $E_{\unicode[STIX]{x1D6FC}}^{0}$
of
$E_{\unicode[STIX]{x1D6FC}}^{0}$
of
![]() $\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })$
over the unit. To summarize, we have constructed the following commutative diagram.
$\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })$
over the unit. To summarize, we have constructed the following commutative diagram.

By construction, the morphism
![]() $\mathfrak{D}$
is compatible with the
$\mathfrak{D}$
is compatible with the
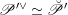 ${\mathscr{P}^{\prime }}^{\vee }\simeq \breve{\mathscr{P}}^{\prime }$
-action, and hence is an equivalence. This finishes the proof of Theorem 5.2.1.
${\mathscr{P}^{\prime }}^{\vee }\simeq \breve{\mathscr{P}}^{\prime }$
-action, and hence is an equivalence. This finishes the proof of Theorem 5.2.1.
5.3 Abelianization theorems
We need to fix a square root
![]() $\unicode[STIX]{x1D705}$
of
$\unicode[STIX]{x1D705}$
of
![]() $\unicode[STIX]{x1D714}_{C}$
. Then the Kostant section for
$\unicode[STIX]{x1D714}_{C}$
. Then the Kostant section for
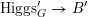 $\operatorname{Higgs}_{G}^{\prime }\rightarrow B^{\prime }$
induces a map
$\operatorname{Higgs}_{G}^{\prime }\rightarrow B^{\prime }$
induces a map
 $$\begin{eqnarray}\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}^{\prime }}:\mathscr{P}^{\prime }\simeq {\operatorname{Higgs}_{G}^{\prime }}^{\text{reg}}\subset \operatorname{Higgs}_{G}^{\prime },\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}^{\prime }}:\mathscr{P}^{\prime }\simeq {\operatorname{Higgs}_{G}^{\prime }}^{\text{reg}}\subset \operatorname{Higgs}_{G}^{\prime },\end{eqnarray}$$
where
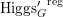 ${\operatorname{Higgs}_{G}^{\prime }}^{\text{reg}}$
is the smooth sub-stack consisting of regular Higgs fields. The first abelianization theorem is the following.
${\operatorname{Higgs}_{G}^{\prime }}^{\text{reg}}$
is the smooth sub-stack consisting of regular Higgs fields. The first abelianization theorem is the following.
Theorem 5.3.1. We have a canonical isomorphism
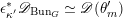 $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}^{\prime }}^{\ast }\mathscr{D}_{\operatorname{Bun}_{G}}\simeq \mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })$
, where
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}^{\prime }}^{\ast }\mathscr{D}_{\operatorname{Bun}_{G}}\simeq \mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })$
, where
![]() $\mathscr{D}_{\operatorname{Bun}_{G}}$
is the
$\mathscr{D}_{\operatorname{Bun}_{G}}$
is the
![]() $\mathbb{G}_{m}$
-gerbe on
$\mathbb{G}_{m}$
-gerbe on
![]() $\operatorname{Higgs}_{G}^{\prime }$
of crystalline differential operators. Moreover, the pullback along the map
$\operatorname{Higgs}_{G}^{\prime }$
of crystalline differential operators. Moreover, the pullback along the map
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}^{\prime }}$
defines an equivalence of categories of twisted sheaves
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}^{\prime }}$
defines an equivalence of categories of twisted sheaves
 $$\begin{eqnarray}\mathfrak{A}_{\unicode[STIX]{x1D705}}:D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G}^{0}))\simeq D^{b}(\operatorname{QCoh}(\mathscr{D}_{\operatorname{ Bun}_{G}}^{0}))_{1}\stackrel{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}^{\prime }}^{\ast }}{\simeq }D^{b}(\operatorname{QCoh}(\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })|_{B^{^{\prime }0}}))_{1}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{A}_{\unicode[STIX]{x1D705}}:D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G}^{0}))\simeq D^{b}(\operatorname{QCoh}(\mathscr{D}_{\operatorname{ Bun}_{G}}^{0}))_{1}\stackrel{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}^{\prime }}^{\ast }}{\simeq }D^{b}(\operatorname{QCoh}(\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })|_{B^{^{\prime }0}}))_{1}.\end{eqnarray}$$
Proof. By Proposition B.3.3, the restriction of
![]() $\mathscr{D}_{\operatorname{Bun}_{G}}$
to
$\mathscr{D}_{\operatorname{Bun}_{G}}$
to
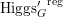 ${\operatorname{Higgs}_{G}^{\prime }}^{\text{reg}}$
is isomorphic to the gerbe
${\operatorname{Higgs}_{G}^{\prime }}^{\text{reg}}$
is isomorphic to the gerbe
![]() $\mathscr{D}(\unicode[STIX]{x1D703}_{\text{can}}^{\prime })$
defined by the canonical 1-form
$\mathscr{D}(\unicode[STIX]{x1D703}_{\text{can}}^{\prime })$
defined by the canonical 1-form
![]() $\unicode[STIX]{x1D703}_{\text{can}}^{\prime }$
on
$\unicode[STIX]{x1D703}_{\text{can}}^{\prime }$
on
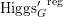 ${\operatorname{Higgs}_{G}^{\prime }}^{\text{reg}}$
. On the other hand, it follows from the construction of
${\operatorname{Higgs}_{G}^{\prime }}^{\text{reg}}$
. On the other hand, it follows from the construction of
![]() $\unicode[STIX]{x1D703}_{m}$
in §4.2 that we have
$\unicode[STIX]{x1D703}_{m}$
in §4.2 that we have
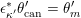 $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}^{\prime }}^{\ast }\unicode[STIX]{x1D703}_{\text{can}}^{\prime }=\unicode[STIX]{x1D703}_{m}^{\prime }$
. Hence
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}^{\prime }}^{\ast }\unicode[STIX]{x1D703}_{\text{can}}^{\prime }=\unicode[STIX]{x1D703}_{m}^{\prime }$
. Hence
 $$\begin{eqnarray}\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}^{\prime }}^{\ast }\mathscr{D}_{\operatorname{ Bun}_{G}}\simeq \unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}^{\prime }}^{\ast }\mathscr{D}(\unicode[STIX]{x1D703}_{\text{can}}^{\prime })\simeq \mathscr{D}(\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}^{\prime }}^{\ast }\unicode[STIX]{x1D703}_{\text{can}})\simeq \mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}^{\prime }}^{\ast }\mathscr{D}_{\operatorname{ Bun}_{G}}\simeq \unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}^{\prime }}^{\ast }\mathscr{D}(\unicode[STIX]{x1D703}_{\text{can}}^{\prime })\simeq \mathscr{D}(\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}^{\prime }}^{\ast }\unicode[STIX]{x1D703}_{\text{can}})\simeq \mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime }).\end{eqnarray}$$
The last statement follows from the fact that the base change of
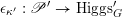 $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}^{\prime }}:\mathscr{P}^{\prime }\rightarrow \operatorname{Higgs}_{G}^{\prime }$
to
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}^{\prime }}:\mathscr{P}^{\prime }\rightarrow \operatorname{Higgs}_{G}^{\prime }$
to
![]() $B^{^{\prime }0}$
is an isomorphism (see Proposition 2.6.1).◻
$B^{^{\prime }0}$
is an isomorphism (see Proposition 2.6.1).◻
To state the second abelianization theorem, recall that in [Reference Chen and ZhuCZ15] we constructed a canonical isomorphism
 $$\begin{eqnarray}\mathfrak{C}:\breve{\mathscr{H}}\times ^{\breve{\mathscr{P}}^{\prime }}\operatorname{Higgs}_{\breve{G}}^{\prime }\simeq \operatorname{LocSys}_{\breve{G}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{C}:\breve{\mathscr{H}}\times ^{\breve{\mathscr{P}}^{\prime }}\operatorname{Higgs}_{\breve{G}}^{\prime }\simeq \operatorname{LocSys}_{\breve{G}}.\end{eqnarray}$$
Moreover, by [Reference Chen and ZhuCZ15, Remark 3.14] the choice of the theta characteristic
![]() $\unicode[STIX]{x1D705}$
defines an isomorphism
$\unicode[STIX]{x1D705}$
defines an isomorphism
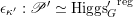 $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}^{\prime }}:\mathscr{P}^{\prime }\simeq {\operatorname{Higgs}_{G}^{\prime }}^{\text{reg}}$
, and hence induces an isomorphism
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}^{\prime }}:\mathscr{P}^{\prime }\simeq {\operatorname{Higgs}_{G}^{\prime }}^{\text{reg}}$
, and hence induces an isomorphism
 $$\begin{eqnarray}\mathfrak{C}_{\unicode[STIX]{x1D705}}:\breve{\mathscr{H}}\simeq \operatorname{LocSys}_{\breve{G}}^{\text{reg}}\subset \operatorname{LocSys}_{\breve{G}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{C}_{\unicode[STIX]{x1D705}}:\breve{\mathscr{H}}\simeq \operatorname{LocSys}_{\breve{G}}^{\text{reg}}\subset \operatorname{LocSys}_{\breve{G}}.\end{eqnarray}$$
Here
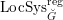 $\operatorname{LocSys}_{\breve{G}}^{\text{reg}}$
is the open substack consisting of
$\operatorname{LocSys}_{\breve{G}}^{\text{reg}}$
is the open substack consisting of
![]() $\breve{G}$
-local systems with regular
$\breve{G}$
-local systems with regular
![]() $p$
-curvature, and we have
$p$
-curvature, and we have
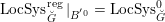 $\operatorname{LocSys}_{\breve{G}}^{\text{reg}}|_{B^{^{\prime }0}}=\operatorname{LocSys}_{\breve{G}}^{0}$
. It implies the following.
$\operatorname{LocSys}_{\breve{G}}^{\text{reg}}|_{B^{^{\prime }0}}=\operatorname{LocSys}_{\breve{G}}^{0}$
. It implies the following.
Theorem 5.3.2. For each choice of a square root
![]() $\unicode[STIX]{x1D705}$
of
$\unicode[STIX]{x1D705}$
of
![]() $\unicode[STIX]{x1D714}_{C}$
, we have a canonical isomorphism of
$\unicode[STIX]{x1D714}_{C}$
, we have a canonical isomorphism of
![]() $\breve{\mathscr{P}}^{\prime }$
-torsors
$\breve{\mathscr{P}}^{\prime }$
-torsors
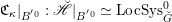 $\mathfrak{C}_{\unicode[STIX]{x1D705}}|_{B^{^{\prime }0}}:\breve{\mathscr{H}}|_{B^{^{\prime }0}}\simeq \operatorname{LocSys}_{\breve{G}}^{0}$
and it induces an equivalence of categories
$\mathfrak{C}_{\unicode[STIX]{x1D705}}|_{B^{^{\prime }0}}:\breve{\mathscr{H}}|_{B^{^{\prime }0}}\simeq \operatorname{LocSys}_{\breve{G}}^{0}$
and it induces an equivalence of categories
 $$\begin{eqnarray}\mathfrak{C}_{\unicode[STIX]{x1D705}}^{\ast }:D^{b}(\operatorname{QCoh}(\operatorname{LocSys}_{\breve{G}}^{0}))\simeq D^{b}(\operatorname{QCoh}(\breve{\mathscr{H}}|_{B^{^{\prime }0}})).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{C}_{\unicode[STIX]{x1D705}}^{\ast }:D^{b}(\operatorname{QCoh}(\operatorname{LocSys}_{\breve{G}}^{0}))\simeq D^{b}(\operatorname{QCoh}(\breve{\mathscr{H}}|_{B^{^{\prime }0}})).\end{eqnarray}$$
5.4 Proof of Theorem 5.0.1
We deduce our main theorem from the twisted duality and above two abelianization theorems. By the twisted duality we have an isomorphism of
 ${\mathscr{P}^{\prime }}^{\vee }\simeq \breve{\mathscr{P}}^{\prime }$
-torsors
${\mathscr{P}^{\prime }}^{\vee }\simeq \breve{\mathscr{P}}^{\prime }$
-torsors
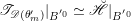 $\mathscr{T}_{\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })}|_{B^{^{\prime }0}}\simeq \breve{\mathscr{H}}|_{B^{^{\prime }0}}$
. Therefore the twisted Fourier–Mukai transform (Theorem A.7.2) implies an equivalence of categories
$\mathscr{T}_{\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })}|_{B^{^{\prime }0}}\simeq \breve{\mathscr{H}}|_{B^{^{\prime }0}}$
. Therefore the twisted Fourier–Mukai transform (Theorem A.7.2) implies an equivalence of categories
 $$\begin{eqnarray}\mathfrak{D}:D^{b}(\operatorname{QCoh}(\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })|_{B^{^{\prime }0}}))_{1}\simeq D^{b}(\operatorname{QCoh}(\breve{\mathscr{H}}|_{B^{^{\prime }0}})).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{D}:D^{b}(\operatorname{QCoh}(\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })|_{B^{^{\prime }0}}))_{1}\simeq D^{b}(\operatorname{QCoh}(\breve{\mathscr{H}}|_{B^{^{\prime }0}})).\end{eqnarray}$$
Now combining Theorems 5.3.1 and 5.3.2 we get the desired equivalence
 $$\begin{eqnarray}\mathfrak{D}_{\unicode[STIX]{x1D705}}=(\mathfrak{C}_{\unicode[STIX]{x1D705}}^{\ast })^{-1}\circ \mathfrak{D}\circ \mathfrak{A}_{\unicode[STIX]{x1D705}}:D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G}^{0}))\simeq D^{b}(\operatorname{QCoh}(\operatorname{LocSys}_{\breve{G}}^{0})).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{D}_{\unicode[STIX]{x1D705}}=(\mathfrak{C}_{\unicode[STIX]{x1D705}}^{\ast })^{-1}\circ \mathfrak{D}\circ \mathfrak{A}_{\unicode[STIX]{x1D705}}:D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G}^{0}))\simeq D^{b}(\operatorname{QCoh}(\operatorname{LocSys}_{\breve{G}}^{0})).\end{eqnarray}$$
5.5 A
 $\unicode[STIX]{x1D707}_{2}$
-gerbe of equivalences
$\unicode[STIX]{x1D707}_{2}$
-gerbe of equivalences
In this subsection we study how those equivalences
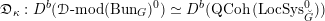 $\mathfrak{D}_{\unicode[STIX]{x1D705}}:D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})^{0})\simeq D^{b}(\operatorname{QCoh}(\operatorname{LocSys}_{\breve{G}}^{0}))$
in Theorem 5.0.1 depend on the choices of the theta characteristics
$\mathfrak{D}_{\unicode[STIX]{x1D705}}:D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})^{0})\simeq D^{b}(\operatorname{QCoh}(\operatorname{LocSys}_{\breve{G}}^{0}))$
in Theorem 5.0.1 depend on the choices of the theta characteristics
![]() $\unicode[STIX]{x1D705}$
. Our discussion is very similar to [Reference Frenkel and WittenFW08] and can be regarded as a verification of the predictions of [Reference Frenkel and WittenFW08] in our setting.
$\unicode[STIX]{x1D705}$
. Our discussion is very similar to [Reference Frenkel and WittenFW08] and can be regarded as a verification of the predictions of [Reference Frenkel and WittenFW08] in our setting.
Let
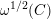 $\unicode[STIX]{x1D714}^{1/2}(C)$
be the groupoid of square roots of
$\unicode[STIX]{x1D714}^{1/2}(C)$
be the groupoid of square roots of
![]() $\unicode[STIX]{x1D714}_{C}$
. The groupoid
$\unicode[STIX]{x1D714}_{C}$
. The groupoid
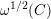 $\unicode[STIX]{x1D714}^{1/2}(C)$
is a torsor over the Picard category
$\unicode[STIX]{x1D714}^{1/2}(C)$
is a torsor over the Picard category
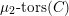 $\unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)$
of
$\unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)$
of
![]() $\unicode[STIX]{x1D707}_{2}$
-torsors on
$\unicode[STIX]{x1D707}_{2}$
-torsors on
![]() $C$
. Let
$C$
. Let
![]() $\mathbf{GLC}$
be the groupoid of equivalences between
$\mathbf{GLC}$
be the groupoid of equivalences between
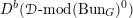 $D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})^{0})$
and
$D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})^{0})$
and
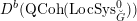 $D^{b}(\operatorname{QCoh}(\operatorname{LocSys}_{\breve{G}}^{0}))$
, i.e., objects in
$D^{b}(\operatorname{QCoh}(\operatorname{LocSys}_{\breve{G}}^{0}))$
, i.e., objects in
![]() $\mathbf{GLC}$
are equivalences
$\mathbf{GLC}$
are equivalences
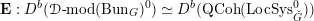 $\mathbf{E}:D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})^{0})\simeq D^{b}(\operatorname{QCoh}(\operatorname{LocSys}_{\breve{G}}^{0}))$
and morphisms are isomorphisms between equivalences. We first construct an action of
$\mathbf{E}:D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})^{0})\simeq D^{b}(\operatorname{QCoh}(\operatorname{LocSys}_{\breve{G}}^{0}))$
and morphisms are isomorphisms between equivalences. We first construct an action of
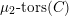 $\unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)$
on
$\unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)$
on
![]() $\mathbf{GLC}$
.
$\mathbf{GLC}$
.
Let
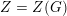 $Z=Z(G)$
be the center of
$Z=Z(G)$
be the center of
![]() $G$
. We have a map
$G$
. We have a map
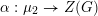 $\unicode[STIX]{x1D6FC}:\unicode[STIX]{x1D707}_{2}\rightarrow Z(G)$
by restricting the cocharacter
$\unicode[STIX]{x1D6FC}:\unicode[STIX]{x1D707}_{2}\rightarrow Z(G)$
by restricting the cocharacter
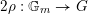 $2\unicode[STIX]{x1D70C}:\mathbb{G}_{m}\rightarrow G$
to
$2\unicode[STIX]{x1D70C}:\mathbb{G}_{m}\rightarrow G$
to
![]() $\unicode[STIX]{x1D707}_{2}$
(see [Reference Beilinson and DrinfeldBD91, §3.4.2]). Thus for each
$\unicode[STIX]{x1D707}_{2}$
(see [Reference Beilinson and DrinfeldBD91, §3.4.2]). Thus for each
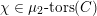 $\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)$
and
$\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)$
and
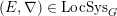 $(E,\unicode[STIX]{x1D6FB})\in \operatorname{LocSys}_{G}$
we can twist
$(E,\unicode[STIX]{x1D6FB})\in \operatorname{LocSys}_{G}$
we can twist
![]() $(E,\unicode[STIX]{x1D6FB})$
by
$(E,\unicode[STIX]{x1D6FB})$
by
![]() $\unicode[STIX]{x1D712}$
using the map
$\unicode[STIX]{x1D712}$
using the map
 $$\begin{eqnarray}\unicode[STIX]{x1D707}_{2}\rightarrow ~Z\rightarrow \operatorname{Aut}(E,\unicode[STIX]{x1D6FB})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{2}\rightarrow ~Z\rightarrow \operatorname{Aut}(E,\unicode[STIX]{x1D6FB})\end{eqnarray}$$
to get a new
![]() $G$
-local system
$G$
-local system
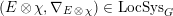 $(E\,\otimes \,\unicode[STIX]{x1D712},\unicode[STIX]{x1D6FB}_{E\,\otimes \,\unicode[STIX]{x1D712}})\in \operatorname{LocSys}_{G}$
. The assignment
$(E\,\otimes \,\unicode[STIX]{x1D712},\unicode[STIX]{x1D6FB}_{E\,\otimes \,\unicode[STIX]{x1D712}})\in \operatorname{LocSys}_{G}$
. The assignment
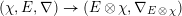 $(\unicode[STIX]{x1D712},E,\unicode[STIX]{x1D6FB})\rightarrow (E\,\otimes \,\unicode[STIX]{x1D712},\unicode[STIX]{x1D6FB}_{E\,\otimes \,\unicode[STIX]{x1D712}})$
defines a geometric action
$(\unicode[STIX]{x1D712},E,\unicode[STIX]{x1D6FB})\rightarrow (E\,\otimes \,\unicode[STIX]{x1D712},\unicode[STIX]{x1D6FB}_{E\,\otimes \,\unicode[STIX]{x1D712}})$
defines a geometric action
 $$\begin{eqnarray}\text{act}_{G}:\unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)\times \operatorname{LocSys}_{G}\rightarrow \operatorname{LocSys}_{G}.\end{eqnarray}$$
$$\begin{eqnarray}\text{act}_{G}:\unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)\times \operatorname{LocSys}_{G}\rightarrow \operatorname{LocSys}_{G}.\end{eqnarray}$$
Likewise, there is
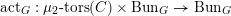 $\text{act}_{G}:\unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)\times \operatorname{Bun}_{G}\rightarrow \operatorname{Bun}_{G}$
. For
$\text{act}_{G}:\unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)\times \operatorname{Bun}_{G}\rightarrow \operatorname{Bun}_{G}$
. For
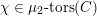 $\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)$
, let
$\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)$
, let
 $a_{\unicode[STIX]{x1D712},G}:\operatorname{Bun}_{G}\simeq \operatorname{Bun}_{G}$
(respectively,
$a_{\unicode[STIX]{x1D712},G}:\operatorname{Bun}_{G}\simeq \operatorname{Bun}_{G}$
(respectively,
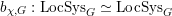 $b_{\unicode[STIX]{x1D712},G}:\operatorname{LocSys}_{G}\simeq \operatorname{LocSys}_{G}$
) be the automorphisms of
$b_{\unicode[STIX]{x1D712},G}:\operatorname{LocSys}_{G}\simeq \operatorname{LocSys}_{G}$
) be the automorphisms of
![]() $\operatorname{Bun}_{G}$
(respectively
$\operatorname{Bun}_{G}$
(respectively
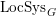 $\operatorname{LocSys}_{G}$
) given by
$\operatorname{LocSys}_{G}$
) given by
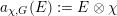 $a_{\unicode[STIX]{x1D712},G}(E):=E\otimes \unicode[STIX]{x1D712}$
, (respectively
$a_{\unicode[STIX]{x1D712},G}(E):=E\otimes \unicode[STIX]{x1D712}$
, (respectively
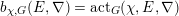 $b_{\unicode[STIX]{x1D712},G}(E,\unicode[STIX]{x1D6FB})=\text{act}_{G}(\unicode[STIX]{x1D712},E,\unicode[STIX]{x1D6FB})$
). They induce auto-equivalences
$b_{\unicode[STIX]{x1D712},G}(E,\unicode[STIX]{x1D6FB})=\text{act}_{G}(\unicode[STIX]{x1D712},E,\unicode[STIX]{x1D6FB})$
). They induce auto-equivalences
![]() $a_{\unicode[STIX]{x1D712},G}^{\ast }$
and
$a_{\unicode[STIX]{x1D712},G}^{\ast }$
and
![]() $b_{\unicode[STIX]{x1D712},G}^{\ast }$
of
$b_{\unicode[STIX]{x1D712},G}^{\ast }$
of
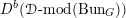 $D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G}))$
and
$D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G}))$
and
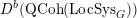 $D^{b}(\operatorname{QCoh}(\operatorname{LocSys}_{G}))$
respectively. Note that for the definition of
$D^{b}(\operatorname{QCoh}(\operatorname{LocSys}_{G}))$
respectively. Note that for the definition of
![]() $a_{\unicode[STIX]{x1D712},G}^{\ast }$
and
$a_{\unicode[STIX]{x1D712},G}^{\ast }$
and
![]() $b_{\unicode[STIX]{x1D712},G}^{\ast }$
, there is no restriction of the characteristic of
$b_{\unicode[STIX]{x1D712},G}^{\ast }$
, there is no restriction of the characteristic of
![]() $k$
. However, if
$k$
. However, if
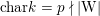 $\operatorname{char}k=p\nmid |\text{W}|$
, we have the following.
$\operatorname{char}k=p\nmid |\text{W}|$
, we have the following.
Lemma 5.5.1.
-
(1) The equivalence
 $a_{\unicode[STIX]{x1D712},G}^{\ast }$
preserves the full subcategory
$a_{\unicode[STIX]{x1D712},G}^{\ast }$
preserves the full subcategory
 $D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})^{0})$
.
$D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})^{0})$
. -
(2) The equivalence
 $b_{\unicode[STIX]{x1D712},G}^{\ast }$
preserves the full subcategory
$b_{\unicode[STIX]{x1D712},G}^{\ast }$
preserves the full subcategory
 $D^{b}(\operatorname{QCoh}(\operatorname{LocSys}_{G}^{0}))$
.
$D^{b}(\operatorname{QCoh}(\operatorname{LocSys}_{G}^{0}))$
.
Proof. This lemma will be clear after we give alternative descriptions of
![]() $a_{\unicode[STIX]{x1D712},G}^{\ast }$
and
$a_{\unicode[STIX]{x1D712},G}^{\ast }$
and
![]() $b_{\unicode[STIX]{x1D712},G}^{\ast }$
.
$b_{\unicode[STIX]{x1D712},G}^{\ast }$
.
First, recall that in §B.3 we introduce a
![]() $\mathbb{G}_{m}$
-gerbe
$\mathbb{G}_{m}$
-gerbe
![]() $\mathscr{D}_{\operatorname{Bun}_{G}}$
over
$\mathscr{D}_{\operatorname{Bun}_{G}}$
over
 $T^{\ast }\operatorname{Bun}_{G}^{\prime }$
and the category
$T^{\ast }\operatorname{Bun}_{G}^{\prime }$
and the category
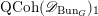 $\operatorname{QCoh}(\mathscr{D}_{\operatorname{Bun}_{G}})_{1}$
of twisted sheaves on
$\operatorname{QCoh}(\mathscr{D}_{\operatorname{Bun}_{G}})_{1}$
of twisted sheaves on
![]() $\mathscr{D}_{\operatorname{Bun}_{G}}$
such that there is an equivalence of categories between
$\mathscr{D}_{\operatorname{Bun}_{G}}$
such that there is an equivalence of categories between
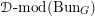 ${\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})$
and
${\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})$
and
 $\operatorname{QCoh}(\mathscr{D}_{\operatorname{Bun}_{G}})_{1}$
. Let
$\operatorname{QCoh}(\mathscr{D}_{\operatorname{Bun}_{G}})_{1}$
. Let
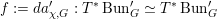 $f:=da_{\unicode[STIX]{x1D712},G}^{\prime }:T^{\ast }\operatorname{Bun}_{G}^{\prime }\simeq T^{\ast }\operatorname{Bun}_{G}^{\prime }$
be the differential of
$f:=da_{\unicode[STIX]{x1D712},G}^{\prime }:T^{\ast }\operatorname{Bun}_{G}^{\prime }\simeq T^{\ast }\operatorname{Bun}_{G}^{\prime }$
be the differential of
![]() $a_{\unicode[STIX]{x1D712},G}^{\prime }$
. The map
$a_{\unicode[STIX]{x1D712},G}^{\prime }$
. The map
![]() $f$
preserves the canonical one form
$f$
preserves the canonical one form
![]() $\unicode[STIX]{x1D703}_{\text{can}}^{\prime }$
, and thus by Lemma B.4.1, there is a canonical 1-morphism
$\unicode[STIX]{x1D703}_{\text{can}}^{\prime }$
, and thus by Lemma B.4.1, there is a canonical 1-morphism
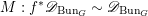 $M:f^{\ast }\mathscr{D}_{\operatorname{Bun}_{G}}\sim \mathscr{D}_{\operatorname{Bun}_{G}}$
of gerbes on
$M:f^{\ast }\mathscr{D}_{\operatorname{Bun}_{G}}\sim \mathscr{D}_{\operatorname{Bun}_{G}}$
of gerbes on
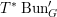 $T^{\ast }\operatorname{Bun}_{G}^{\prime }$
. The 1-morphism
$T^{\ast }\operatorname{Bun}_{G}^{\prime }$
. The 1-morphism
![]() $M$
induces an equivalence
$M$
induces an equivalence
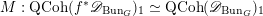 $M:\operatorname{QCoh}(f^{\ast }\mathscr{D}_{\operatorname{Bun}_{G}})_{1}\simeq \operatorname{QCoh}(\mathscr{D}_{\operatorname{Bun}_{G}})_{1}$
and it follows from definitions that the functor
$M:\operatorname{QCoh}(f^{\ast }\mathscr{D}_{\operatorname{Bun}_{G}})_{1}\simeq \operatorname{QCoh}(\mathscr{D}_{\operatorname{Bun}_{G}})_{1}$
and it follows from definitions that the functor
![]() $a_{\unicode[STIX]{x1D712},G}^{\ast }$
is isomorphic to the composition
$a_{\unicode[STIX]{x1D712},G}^{\ast }$
is isomorphic to the composition
 $$\begin{eqnarray}D^{b}(\operatorname{QCoh}(\mathscr{D}_{\operatorname{ Bun}_{G}})_{1})\stackrel{~f^{\ast }}{\simeq }D^{b}(\operatorname{QCoh}(f^{\ast }\mathscr{D}_{\operatorname{ Bun}_{G}})_{1})\stackrel{M}{\simeq }D^{b}(\operatorname{QCoh}(\mathscr{D}_{\operatorname{ Bun}_{G}})_{1}).\end{eqnarray}$$
$$\begin{eqnarray}D^{b}(\operatorname{QCoh}(\mathscr{D}_{\operatorname{ Bun}_{G}})_{1})\stackrel{~f^{\ast }}{\simeq }D^{b}(\operatorname{QCoh}(f^{\ast }\mathscr{D}_{\operatorname{ Bun}_{G}})_{1})\stackrel{M}{\simeq }D^{b}(\operatorname{QCoh}(\mathscr{D}_{\operatorname{ Bun}_{G}})_{1}).\end{eqnarray}$$
Recall that the category
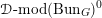 ${\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})^{0}$
is by definition the category of twisted sheaves on
${\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})^{0}$
is by definition the category of twisted sheaves on
 $\mathscr{D}_{\operatorname{Bun}_{G}}^{0}=\mathscr{D}_{\operatorname{Bun}_{G}}|_{B^{^{\prime }0}}$
. Therefore, part (1) follows.
$\mathscr{D}_{\operatorname{Bun}_{G}}^{0}=\mathscr{D}_{\operatorname{Bun}_{G}}|_{B^{^{\prime }0}}$
. Therefore, part (1) follows.
To prove part (2), note that the map
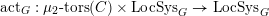 $\text{act}_{G}:\unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)\times \operatorname{LocSys}_{G}\rightarrow \operatorname{LocSys}_{G}$
can be also described as follows. There is a map of group schemes
$\text{act}_{G}:\unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)\times \operatorname{LocSys}_{G}\rightarrow \operatorname{LocSys}_{G}$
can be also described as follows. There is a map of group schemes
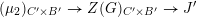 $(\unicode[STIX]{x1D707}_{2})_{C^{\prime }\times B^{\prime }}\rightarrow Z(G)_{C^{\prime }\times B^{\prime }}\rightarrow J^{\prime }$
over
$(\unicode[STIX]{x1D707}_{2})_{C^{\prime }\times B^{\prime }}\rightarrow Z(G)_{C^{\prime }\times B^{\prime }}\rightarrow J^{\prime }$
over
 $C^{\prime }\times B^{\prime }$
, which induces a morphism of Picard stacks
$C^{\prime }\times B^{\prime }$
, which induces a morphism of Picard stacks
 $$\begin{eqnarray}\mathfrak{l}_{\unicode[STIX]{x1D707}_{2}}:\unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)\times B^{\prime }\rightarrow \mathscr{P}^{\prime },\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{l}_{\unicode[STIX]{x1D707}_{2}}:\unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)\times B^{\prime }\rightarrow \mathscr{P}^{\prime },\end{eqnarray}$$
and the action map
![]() $\text{act}_{G}$
can be identified with
$\text{act}_{G}$
can be identified with
 $$\begin{eqnarray}\text{act}_{G}:\unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)\times \operatorname{LocSys}_{G}\stackrel{\mathfrak{l}_{\unicode[STIX]{x1D707}_{2}}\times \text{id}}{\rightarrow }\mathscr{P}^{\prime }\times _{B^{\prime }}\operatorname{LocSys}_{G}\rightarrow \operatorname{LocSys}_{G}\end{eqnarray}$$
$$\begin{eqnarray}\text{act}_{G}:\unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)\times \operatorname{LocSys}_{G}\stackrel{\mathfrak{l}_{\unicode[STIX]{x1D707}_{2}}\times \text{id}}{\rightarrow }\mathscr{P}^{\prime }\times _{B^{\prime }}\operatorname{LocSys}_{G}\rightarrow \operatorname{LocSys}_{G}\end{eqnarray}$$
where the last map is the action of
![]() $\mathscr{P}^{\prime }$
on
$\mathscr{P}^{\prime }$
on
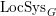 $\operatorname{LocSys}_{G}$
defined in [Reference Chen and ZhuCZ15, Proposition 3.5]. In particular, if we endow
$\operatorname{LocSys}_{G}$
defined in [Reference Chen and ZhuCZ15, Proposition 3.5]. In particular, if we endow
![]() $B^{\prime }$
with the trivial
$B^{\prime }$
with the trivial
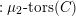 $:\unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)$
action, the
$:\unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)$
action, the
![]() $p$
-Hitchin map
$p$
-Hitchin map
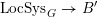 $\operatorname{LocSys}_{G}\rightarrow B^{\prime }$
is
$\operatorname{LocSys}_{G}\rightarrow B^{\prime }$
is
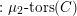 $:\unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)$
-equivariant. Therefore
$:\unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)$
-equivariant. Therefore
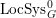 $\operatorname{LocSys}_{G}^{0}$
is invariant under the action of
$\operatorname{LocSys}_{G}^{0}$
is invariant under the action of
![]() $b_{\unicode[STIX]{x1D712},G}$
, and part (2) follows.◻
$b_{\unicode[STIX]{x1D712},G}$
, and part (2) follows.◻
From now on we regard
![]() $a_{\unicode[STIX]{x1D712},G}^{\ast }$
and
$a_{\unicode[STIX]{x1D712},G}^{\ast }$
and
![]() $b_{\unicode[STIX]{x1D712},G}^{\ast }$
as automorphisms of the category
$b_{\unicode[STIX]{x1D712},G}^{\ast }$
as automorphisms of the category
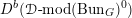 $D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})^{0})$
and
$D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})^{0})$
and
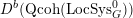 $D^{b}(\operatorname{Qcoh}(\operatorname{LocSys}_{G}^{0}))$
.
$D^{b}(\operatorname{Qcoh}(\operatorname{LocSys}_{G}^{0}))$
.
For each
 $\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D707}_{2}\operatorname{tors}(C)$
and
$\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D707}_{2}\operatorname{tors}(C)$
and
 $\mathbf{E}\in \mathbf{GLC}$
we define
$\mathbf{E}\in \mathbf{GLC}$
we define
 $$\begin{eqnarray}\unicode[STIX]{x1D712}\cdot \mathbf{E}:=b_{\unicode[STIX]{x1D712},\breve{G}}^{\ast }\circ \mathbf{E}\circ a_{\unicode[STIX]{x1D712},G}^{\ast }\in \mathbf{GLC}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}\cdot \mathbf{E}:=b_{\unicode[STIX]{x1D712},\breve{G}}^{\ast }\circ \mathbf{E}\circ a_{\unicode[STIX]{x1D712},G}^{\ast }\in \mathbf{GLC}.\end{eqnarray}$$
The following lemma follows from the construction of
![]() $b_{\unicode[STIX]{x1D712},\breve{G}}^{\ast }$
and
$b_{\unicode[STIX]{x1D712},\breve{G}}^{\ast }$
and
![]() $a_{\unicode[STIX]{x1D712},G}^{\ast }$
.
$a_{\unicode[STIX]{x1D712},G}^{\ast }$
.
Lemma 5.5.2. The functor
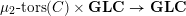 $\unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)\times \mathbf{GLC}\rightarrow \mathbf{GLC}$
given by
$\unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)\times \mathbf{GLC}\rightarrow \mathbf{GLC}$
given by
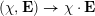 $(\unicode[STIX]{x1D712},\mathbf{E})\rightarrow \unicode[STIX]{x1D712}\cdot \mathbf{E}$
defines an action of the Picard category
$(\unicode[STIX]{x1D712},\mathbf{E})\rightarrow \unicode[STIX]{x1D712}\cdot \mathbf{E}$
defines an action of the Picard category
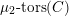 $\unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)$
on
$\unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)$
on
![]() $\mathbf{GLC}$
.
$\mathbf{GLC}$
.
Now let
![]() $\mathscr{C}_{1}$
and
$\mathscr{C}_{1}$
and
![]() $\mathscr{C}_{2}$
be two categories acted by a Picard category
$\mathscr{C}_{2}$
be two categories acted by a Picard category
![]() $\mathscr{G}$
. A
$\mathscr{G}$
. A
![]() $\mathscr{G}$
-module functor from
$\mathscr{G}$
-module functor from
![]() $\mathscr{C}_{1}$
to
$\mathscr{C}_{1}$
to
![]() $\mathscr{C}_{2}$
is a functor
$\mathscr{C}_{2}$
is a functor
 $N:\mathscr{C}_{1}\rightarrow \mathscr{C}_{2}$
equipped with functorial isomorphisms
$N:\mathscr{C}_{1}\rightarrow \mathscr{C}_{2}$
equipped with functorial isomorphisms
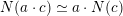 $N(a\cdot c)\simeq a\cdot N(c)$
satisfying the natural compatibility condition. Here is the main result of this subsection.
$N(a\cdot c)\simeq a\cdot N(c)$
satisfying the natural compatibility condition. Here is the main result of this subsection.
Proposition 5.5.3. The assignment
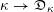 $\unicode[STIX]{x1D705}\rightarrow \mathfrak{D}_{\unicode[STIX]{x1D705}}$
defines a
$\unicode[STIX]{x1D705}\rightarrow \mathfrak{D}_{\unicode[STIX]{x1D705}}$
defines a
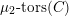 $\unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)$
-module functor
$\unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)$
-module functor
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}:\unicode[STIX]{x1D714}^{1/2}(C)\rightarrow \mathbf{GLC}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}:\unicode[STIX]{x1D714}^{1/2}(C)\rightarrow \mathbf{GLC}.\end{eqnarray}$$
Proof. Given
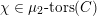 $\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)$
and
$\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)$
and
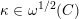 $\unicode[STIX]{x1D705}\in \unicode[STIX]{x1D714}^{1/2}(C)$
we need to specify a functorial isomorphism
$\unicode[STIX]{x1D705}\in \unicode[STIX]{x1D714}^{1/2}(C)$
we need to specify a functorial isomorphism
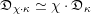 $\mathfrak{D}_{\unicode[STIX]{x1D712}\cdot \unicode[STIX]{x1D705}}\simeq \unicode[STIX]{x1D712}\cdot \mathfrak{D}_{\unicode[STIX]{x1D705}}$
satisfying the natural compatibility condition. First, observe that the maps
$\mathfrak{D}_{\unicode[STIX]{x1D712}\cdot \unicode[STIX]{x1D705}}\simeq \unicode[STIX]{x1D712}\cdot \mathfrak{D}_{\unicode[STIX]{x1D705}}$
satisfying the natural compatibility condition. First, observe that the maps
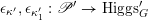 $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}^{\prime }},\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}_{1}^{\prime }}:\mathscr{P}^{\prime }\rightarrow \operatorname{Higgs}_{G}^{\prime }$
induced by
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}^{\prime }},\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}_{1}^{\prime }}:\mathscr{P}^{\prime }\rightarrow \operatorname{Higgs}_{G}^{\prime }$
induced by
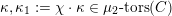 $\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}_{1}:=\unicode[STIX]{x1D712}\cdot \unicode[STIX]{x1D705}\in \unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)$
differ by a translation of the section
$\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}_{1}:=\unicode[STIX]{x1D712}\cdot \unicode[STIX]{x1D705}\in \unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)$
differ by a translation of the section
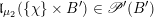 $\mathfrak{l}_{\unicode[STIX]{x1D707}_{2}}(\{\unicode[STIX]{x1D712}\}\times B^{\prime })\in \mathscr{P}^{\prime }(B^{\prime })$
, where
$\mathfrak{l}_{\unicode[STIX]{x1D707}_{2}}(\{\unicode[STIX]{x1D712}\}\times B^{\prime })\in \mathscr{P}^{\prime }(B^{\prime })$
, where
![]() $\mathfrak{l}_{\unicode[STIX]{x1D707}_{2}}$
is the map in (5.5.2). Then it follows from the construction of
$\mathfrak{l}_{\unicode[STIX]{x1D707}_{2}}$
is the map in (5.5.2). Then it follows from the construction of
![]() $\mathfrak{A}_{\unicode[STIX]{x1D705}}$
and
$\mathfrak{A}_{\unicode[STIX]{x1D705}}$
and
![]() $\mathfrak{C}_{\unicode[STIX]{x1D705}}$
in §5.3 that there are canonical functorial isomorphisms
$\mathfrak{C}_{\unicode[STIX]{x1D705}}$
in §5.3 that there are canonical functorial isomorphisms
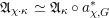 $\mathfrak{A}_{\unicode[STIX]{x1D712}\cdot \unicode[STIX]{x1D705}}\simeq \mathfrak{A}_{\unicode[STIX]{x1D705}}\circ a_{\unicode[STIX]{x1D712},G}^{\ast }$
and
$\mathfrak{A}_{\unicode[STIX]{x1D712}\cdot \unicode[STIX]{x1D705}}\simeq \mathfrak{A}_{\unicode[STIX]{x1D705}}\circ a_{\unicode[STIX]{x1D712},G}^{\ast }$
and
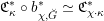 $\mathfrak{C}_{\unicode[STIX]{x1D705}}^{\ast }\circ b_{\unicode[STIX]{x1D712},\breve{G}}^{\ast }\simeq \mathfrak{C}_{\unicode[STIX]{x1D712}\cdot \unicode[STIX]{x1D705}}^{\ast }$
. Therefore we get a functorial isomorphism
$\mathfrak{C}_{\unicode[STIX]{x1D705}}^{\ast }\circ b_{\unicode[STIX]{x1D712},\breve{G}}^{\ast }\simeq \mathfrak{C}_{\unicode[STIX]{x1D712}\cdot \unicode[STIX]{x1D705}}^{\ast }$
. Therefore we get a functorial isomorphism
 $$\begin{eqnarray}\mathfrak{D}_{\unicode[STIX]{x1D712}\cdot \unicode[STIX]{x1D705}}=(\mathfrak{C}_{\unicode[STIX]{x1D712}\cdot \unicode[STIX]{x1D705}}^{\ast })^{-1}\circ \mathfrak{D}\circ \mathfrak{A}_{\unicode[STIX]{x1D712}\cdot \unicode[STIX]{x1D705}}\simeq b_{\unicode[STIX]{x1D712},\breve{G}}^{\ast }\circ (\mathfrak{C}_{\unicode[STIX]{x1D705}}^{\ast })^{-1}\circ \mathfrak{D}\circ \mathfrak{A}_{\unicode[STIX]{x1D705}}\circ a_{\unicode[STIX]{x1D712},G}^{\ast }=\unicode[STIX]{x1D712}\cdot \mathfrak{D}_{\unicode[STIX]{x1D705}},\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{D}_{\unicode[STIX]{x1D712}\cdot \unicode[STIX]{x1D705}}=(\mathfrak{C}_{\unicode[STIX]{x1D712}\cdot \unicode[STIX]{x1D705}}^{\ast })^{-1}\circ \mathfrak{D}\circ \mathfrak{A}_{\unicode[STIX]{x1D712}\cdot \unicode[STIX]{x1D705}}\simeq b_{\unicode[STIX]{x1D712},\breve{G}}^{\ast }\circ (\mathfrak{C}_{\unicode[STIX]{x1D705}}^{\ast })^{-1}\circ \mathfrak{D}\circ \mathfrak{A}_{\unicode[STIX]{x1D705}}\circ a_{\unicode[STIX]{x1D712},G}^{\ast }=\unicode[STIX]{x1D712}\cdot \mathfrak{D}_{\unicode[STIX]{x1D705}},\end{eqnarray}$$
and one can check that it satisfies the natural compatibility condition. ◻
Remark 5.5.4. The above construction suggests that the geometric Langlands correspondence should be a
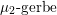 $\unicode[STIX]{x1D707}_{2}\text{-}\text{gerbe}$
of equivalences between
$\unicode[STIX]{x1D707}_{2}\text{-}\text{gerbe}$
of equivalences between
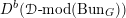 $D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G}))$
and
$D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G}))$
and
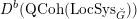 $D^{b}(\operatorname{QCoh}(\operatorname{LocSys}_{\breve{G}}))$
. This gerbe is trivial, but is not canonically trivialized. One obtains a particular trivialization of this gerbe, and hence a particular equivalence
$D^{b}(\operatorname{QCoh}(\operatorname{LocSys}_{\breve{G}}))$
. This gerbe is trivial, but is not canonically trivialized. One obtains a particular trivialization of this gerbe, and hence a particular equivalence
![]() $\mathfrak{D}_{\unicode[STIX]{x1D705}}$
, for each choice of a square root of the canonical line bundle of
$\mathfrak{D}_{\unicode[STIX]{x1D705}}$
, for each choice of a square root of the canonical line bundle of
![]() $C$
. A similar
$C$
. A similar
![]() $\unicode[STIX]{x1D707}_{2}$
-gerbe also appears in the work of Frenkel and Witten [Reference Frenkel and WittenFW08, §10], where the geometric Langlands correspondence is interpreted as gauge theory duality between the twisted
$\unicode[STIX]{x1D707}_{2}$
-gerbe also appears in the work of Frenkel and Witten [Reference Frenkel and WittenFW08, §10], where the geometric Langlands correspondence is interpreted as gauge theory duality between the twisted
![]() $A$
-model of
$A$
-model of
![]() $\operatorname{Higgs}_{G}$
and the twisted
$\operatorname{Higgs}_{G}$
and the twisted
![]() $B$
-model of
$B$
-model of
![]() $\operatorname{Higgs}_{\breve{G}}$
.
$\operatorname{Higgs}_{\breve{G}}$
.
5.6 The actions
 $a_{\unicode[STIX]{x1D712},G}^{\ast }$
and
$a_{\unicode[STIX]{x1D712},G}^{\ast }$
and
 $b_{\unicode[STIX]{x1D712},G}^{\ast }$
as tensoring of line bundles
$b_{\unicode[STIX]{x1D712},G}^{\ast }$
as tensoring of line bundles
In this subsection we show that, under the equivalence
![]() $\mathfrak{D}_{\unicode[STIX]{x1D705}}$
, the geometric actions
$\mathfrak{D}_{\unicode[STIX]{x1D705}}$
, the geometric actions
![]() $a_{\unicode[STIX]{x1D712},G}^{\ast }$
and
$a_{\unicode[STIX]{x1D712},G}^{\ast }$
and
![]() $b_{\unicode[STIX]{x1D712},G}^{\ast }$
constructed in the previous subsection become functors of tensoring with certain line bundles.
$b_{\unicode[STIX]{x1D712},G}^{\ast }$
constructed in the previous subsection become functors of tensoring with certain line bundles.
Recall that in §3.7 we associated to every
![]() $Z(\breve{G})$
-torsor
$Z(\breve{G})$
-torsor
![]() $K$
on
$K$
on
![]() $C$
a line bundle
$C$
a line bundle
![]() ${\mathcal{L}}_{G,K}$
on
${\mathcal{L}}_{G,K}$
on
![]() $\operatorname{Bun}_{G}$
. For any
$\operatorname{Bun}_{G}$
. For any
 $\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)$
let
$\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)$
let
 $K_{G,\unicode[STIX]{x1D712}}:=\unicode[STIX]{x1D712}\times ^{\unicode[STIX]{x1D707}_{2}}Z_{G}\in Z(G)\text{-}\text{tors}(C)$
be the induced
$K_{G,\unicode[STIX]{x1D712}}:=\unicode[STIX]{x1D712}\times ^{\unicode[STIX]{x1D707}_{2}}Z_{G}\in Z(G)\text{-}\text{tors}(C)$
be the induced
![]() $Z(G)$
-torsor via the canonical map
$Z(G)$
-torsor via the canonical map
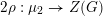 $2\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D707}_{2}\rightarrow Z(G)$
. We denote by
$2\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D707}_{2}\rightarrow Z(G)$
. We denote by
![]() ${\mathcal{L}}_{G,\unicode[STIX]{x1D712}}$
and
${\mathcal{L}}_{G,\unicode[STIX]{x1D712}}$
and
![]() ${\mathcal{L}}_{\breve{G},\unicode[STIX]{x1D712}}$
be the line bundles on
${\mathcal{L}}_{\breve{G},\unicode[STIX]{x1D712}}$
be the line bundles on
![]() $\operatorname{Bun}_{G}$
and
$\operatorname{Bun}_{G}$
and
![]() $\operatorname{Bun}_{\breve{G}}$
corresponding to
$\operatorname{Bun}_{\breve{G}}$
corresponding to
![]() $K_{\breve{G},\unicode[STIX]{x1D712}}$
and
$K_{\breve{G},\unicode[STIX]{x1D712}}$
and
![]() $K_{G,\unicode[STIX]{x1D712}}$
. Since the line bundle
$K_{G,\unicode[STIX]{x1D712}}$
. Since the line bundle
![]() ${\mathcal{L}}_{G,\unicode[STIX]{x1D712}}$
carries a canonical connection with zero
${\mathcal{L}}_{G,\unicode[STIX]{x1D712}}$
carries a canonical connection with zero
![]() $p$
-curvature, tensoring with
$p$
-curvature, tensoring with
![]() ${\mathcal{L}}_{G,\unicode[STIX]{x1D712}}$
defines an auto-equivalence
${\mathcal{L}}_{G,\unicode[STIX]{x1D712}}$
defines an auto-equivalence
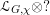 ${\mathcal{L}}_{G,\unicode[STIX]{x1D712}}\otimes ?$
of
${\mathcal{L}}_{G,\unicode[STIX]{x1D712}}\otimes ?$
of
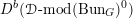 $D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})^{0})$
.
$D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})^{0})$
.
For any
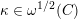 $\unicode[STIX]{x1D705}\in \unicode[STIX]{x1D714}^{1/2}(C)$
let
$\unicode[STIX]{x1D705}\in \unicode[STIX]{x1D714}^{1/2}(C)$
let
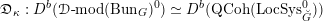 $\mathfrak{D}_{\unicode[STIX]{x1D705}}:D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})^{0})\simeq D^{b}(\operatorname{QCoh}(\operatorname{LocSys}_{\breve{G}}^{0}))$
be the equivalence in Theorem 5.0.1.
$\mathfrak{D}_{\unicode[STIX]{x1D705}}:D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})^{0})\simeq D^{b}(\operatorname{QCoh}(\operatorname{LocSys}_{\breve{G}}^{0}))$
be the equivalence in Theorem 5.0.1.
Theorem 5.6.1. We have the following.
-
(1) The equivalence
 $\mathfrak{D}_{\unicode[STIX]{x1D705}}$
intertwines the auto-equivalence
$\mathfrak{D}_{\unicode[STIX]{x1D705}}$
intertwines the auto-equivalence
 ${\mathcal{L}}_{G,\unicode[STIX]{x1D712}}\otimes ?$
of
${\mathcal{L}}_{G,\unicode[STIX]{x1D712}}\otimes ?$
of
 $D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})^{0})$
and the auto-equivalence
$D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})^{0})$
and the auto-equivalence
 $b_{\unicode[STIX]{x1D712},\breve{G}}^{\ast }$
on
$b_{\unicode[STIX]{x1D712},\breve{G}}^{\ast }$
on
 $D^{b}(\operatorname{QCoh}(\operatorname{LocSys}_{\breve{G}}^{0}))$
constructed in §5.5.
$D^{b}(\operatorname{QCoh}(\operatorname{LocSys}_{\breve{G}}^{0}))$
constructed in §5.5. -
(2) The equivalence
 $\mathfrak{D}_{\unicode[STIX]{x1D705}}$
intertwines the auto-equivalence
$\mathfrak{D}_{\unicode[STIX]{x1D705}}$
intertwines the auto-equivalence
 $a_{\unicode[STIX]{x1D712},G}^{\ast }$
of
$a_{\unicode[STIX]{x1D712},G}^{\ast }$
of
 $D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})^{0})$
as in §5.5 and the auto-equivalence
$D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G})^{0})$
as in §5.5 and the auto-equivalence
 ${\mathcal{L}}_{\breve{G},\unicode[STIX]{x1D712}}\otimes ?$
on
${\mathcal{L}}_{\breve{G},\unicode[STIX]{x1D712}}\otimes ?$
on
 $D^{b}(\operatorname{QCoh}(\operatorname{LocSys}_{\breve{G}}^{0}))$
(here we regard
$D^{b}(\operatorname{QCoh}(\operatorname{LocSys}_{\breve{G}}^{0}))$
(here we regard
 ${\mathcal{L}}_{\breve{G},\unicode[STIX]{x1D712}}$
as a line bundle on
${\mathcal{L}}_{\breve{G},\unicode[STIX]{x1D712}}$
as a line bundle on
 $\operatorname{LocSys}_{\breve{G}}^{0}$
via the projection
$\operatorname{LocSys}_{\breve{G}}^{0}$
via the projection
 $\operatorname{LocSys}_{\breve{G}}\rightarrow \operatorname{Bun}_{\breve{G}}$
).
$\operatorname{LocSys}_{\breve{G}}\rightarrow \operatorname{Bun}_{\breve{G}}$
).
Remark 5.6.2. Similar actions by tensoring line bundles on
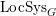 $\operatorname{LocSys}_{G}$
and on
$\operatorname{LocSys}_{G}$
and on
![]() $\operatorname{Higgs}_{G}$
also appear in the work of Frenkel and Witten [Reference Frenkel and WittenFW08, §10.4]. Moreover, the authors also predict that the geometric Langlands correspondence should interchange these actions.
$\operatorname{Higgs}_{G}$
also appear in the work of Frenkel and Witten [Reference Frenkel and WittenFW08, §10.4]. Moreover, the authors also predict that the geometric Langlands correspondence should interchange these actions.
Combining Theorems 5.5.3 and 5.6.1 we have the following.
Corollary 5.6.3. Let
 $\unicode[STIX]{x1D705}_{1},\unicode[STIX]{x1D705}_{2}\in \unicode[STIX]{x1D714}^{1/2}(C)$
. Then there is a natural isomorphism of equivalences
$\unicode[STIX]{x1D705}_{1},\unicode[STIX]{x1D705}_{2}\in \unicode[STIX]{x1D714}^{1/2}(C)$
. Then there is a natural isomorphism of equivalences
 $$\begin{eqnarray}\mathfrak{D}_{\unicode[STIX]{x1D705}_{1}}\simeq ({\mathcal{L}}_{\breve{G},\unicode[STIX]{x1D712}}\otimes ~?)\circ \mathfrak{D}_{\unicode[STIX]{x1D705}_{2}}\circ ({\mathcal{L}}_{G,\unicode[STIX]{x1D712}}\otimes ~?).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{D}_{\unicode[STIX]{x1D705}_{1}}\simeq ({\mathcal{L}}_{\breve{G},\unicode[STIX]{x1D712}}\otimes ~?)\circ \mathfrak{D}_{\unicode[STIX]{x1D705}_{2}}\circ ({\mathcal{L}}_{G,\unicode[STIX]{x1D712}}\otimes ~?).\end{eqnarray}$$
Here
 $\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)$
such that
$\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D707}_{2}\text{-}\text{tors}(C)$
such that
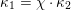 $\unicode[STIX]{x1D705}_{1}=\unicode[STIX]{x1D712}\cdot \unicode[STIX]{x1D705}_{2}$
and
$\unicode[STIX]{x1D705}_{1}=\unicode[STIX]{x1D712}\cdot \unicode[STIX]{x1D705}_{2}$
and
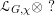 ${\mathcal{L}}_{G,\unicode[STIX]{x1D712}}\otimes ~?$
(respectively
${\mathcal{L}}_{G,\unicode[STIX]{x1D712}}\otimes ~?$
(respectively
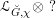 ${\mathcal{L}}_{\breve{G},\unicode[STIX]{x1D712}}\otimes ~?$
) is the functor of tensoring with the line bundle
${\mathcal{L}}_{\breve{G},\unicode[STIX]{x1D712}}\otimes ~?$
) is the functor of tensoring with the line bundle
![]() ${\mathcal{L}}_{G,\unicode[STIX]{x1D712}}$
(respectively
${\mathcal{L}}_{G,\unicode[STIX]{x1D712}}$
(respectively
![]() ${\mathcal{L}}_{\breve{G},\unicode[STIX]{x1D712}}$
).
${\mathcal{L}}_{\breve{G},\unicode[STIX]{x1D712}}$
).
The rest of this subsection is devoted to the proof of this theorem.
We first introduce a morphism of Picard stack
 $$\begin{eqnarray}\tilde{\mathfrak{l}}:Z(G)\text{-}\text{tors}(C)\times B^{\prime }\rightarrow \operatorname{Pic}(\breve{\mathscr{H}})\end{eqnarray}$$
$$\begin{eqnarray}\tilde{\mathfrak{l}}:Z(G)\text{-}\text{tors}(C)\times B^{\prime }\rightarrow \operatorname{Pic}(\breve{\mathscr{H}})\end{eqnarray}$$
and prove a twisted version of Proposition 3.7.4. We begin with the construction of
![]() $\tilde{\mathfrak{l}}$
. Let
$\tilde{\mathfrak{l}}$
. Let
![]() $\operatorname{Bun}_{J^{p}}$
be the Picard stack of
$\operatorname{Bun}_{J^{p}}$
be the Picard stack of
![]() $J^{p}$
-torsors over
$J^{p}$
-torsors over
![]() $C$
. We have the generalized Chern class map
$C$
. We have the generalized Chern class map
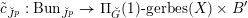 $\tilde{c}_{\breve{J}^{p}}:\operatorname{Bun}_{\breve{J}^{p}}\rightarrow \unicode[STIX]{x1D6F1}_{\breve{G}}(1)\text{-}\text{gerbes}(X)\times B^{\prime }$
and a Picard functor
$\tilde{c}_{\breve{J}^{p}}:\operatorname{Bun}_{\breve{J}^{p}}\rightarrow \unicode[STIX]{x1D6F1}_{\breve{G}}(1)\text{-}\text{gerbes}(X)\times B^{\prime }$
and a Picard functor
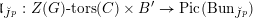 $\mathfrak{l}_{\breve{J}^{p}}:Z(G)\text{-}\text{tors}(C)\times B^{\prime }\rightarrow \operatorname{Pic}(\operatorname{Bun}_{\breve{J}^{p}})$
. We define
$\mathfrak{l}_{\breve{J}^{p}}:Z(G)\text{-}\text{tors}(C)\times B^{\prime }\rightarrow \operatorname{Pic}(\operatorname{Bun}_{\breve{J}^{p}})$
. We define
 $$\begin{eqnarray}\tilde{\mathfrak{l}}:Z(G)\text{-}\text{tors}(C)\times B^{\prime }\stackrel{\mathfrak{l}_{\breve{J}^{p}}}{\rightarrow }\operatorname{Pic}(\operatorname{Bun}_{\breve{J}^{p}})\rightarrow \operatorname{Pic}(\breve{\mathscr{H}})\end{eqnarray}$$
$$\begin{eqnarray}\tilde{\mathfrak{l}}:Z(G)\text{-}\text{tors}(C)\times B^{\prime }\stackrel{\mathfrak{l}_{\breve{J}^{p}}}{\rightarrow }\operatorname{Pic}(\operatorname{Bun}_{\breve{J}^{p}})\rightarrow \operatorname{Pic}(\breve{\mathscr{H}})\end{eqnarray}$$
where the last map is induced by the restriction map
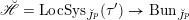 $\breve{\mathscr{H}}=\operatorname{LocSys}_{\breve{J}^{p}}(\unicode[STIX]{x1D70F}^{\prime })\rightarrow \operatorname{Bun}_{\breve{J}^{p}}$
.
$\breve{\mathscr{H}}=\operatorname{LocSys}_{\breve{J}^{p}}(\unicode[STIX]{x1D70F}^{\prime })\rightarrow \operatorname{Bun}_{\breve{J}^{p}}$
.
Recall the morphism
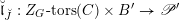 $\breve{\mathfrak{l}}_{\breve{J}}:Z_{G}\text{-}\text{tors}(C)\times B^{\prime }\rightarrow \mathscr{P}^{\prime }$
constructed in §3.7. For any
$\breve{\mathfrak{l}}_{\breve{J}}:Z_{G}\text{-}\text{tors}(C)\times B^{\prime }\rightarrow \mathscr{P}^{\prime }$
constructed in §3.7. For any
![]() $Z(G)$
-torsor
$Z(G)$
-torsor
![]() $K$
over
$K$
over
![]() $C$
, we define
$C$
, we define
 $$\begin{eqnarray}{\mathcal{L}}_{\breve{J}^{p},K}:=\tilde{\mathfrak{l}}(\{K\}\times B^{\prime })\in \operatorname{Pic}(\breve{\mathscr{H}}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}_{\breve{J}^{p},K}:=\tilde{\mathfrak{l}}(\{K\}\times B^{\prime })\in \operatorname{Pic}(\breve{\mathscr{H}}).\end{eqnarray}$$
Let
![]() $K^{\prime }$
denote the Frobenius descendent of
$K^{\prime }$
denote the Frobenius descendent of
![]() $K$
(as
$K$
(as
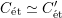 $C_{\acute{\text{e}}\text{t}}\simeq C_{\acute{\text{e}}\text{t}}^{\prime }$
), and let
$C_{\acute{\text{e}}\text{t}}\simeq C_{\acute{\text{e}}\text{t}}^{\prime }$
), and let
 $$\begin{eqnarray}K_{J^{\prime }}^{\prime }=\breve{\mathfrak{l}}_{\breve{J}}(\{K^{\prime }\}\times B^{\prime })\in \mathscr{P}^{\prime }(B^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}K_{J^{\prime }}^{\prime }=\breve{\mathfrak{l}}_{\breve{J}}(\{K^{\prime }\}\times B^{\prime })\in \mathscr{P}^{\prime }(B^{\prime }).\end{eqnarray}$$
We will relate
![]() ${\mathcal{L}}_{\breve{J}^{p},K}$
with
${\mathcal{L}}_{\breve{J}^{p},K}$
with
![]() $K_{J^{\prime }}^{\prime }$
via the twisted duality. From the definition of
$K_{J^{\prime }}^{\prime }$
via the twisted duality. From the definition of
![]() $\unicode[STIX]{x1D703}_{m}^{\prime }$
in §4.2, one can easily check that the restriction of
$\unicode[STIX]{x1D703}_{m}^{\prime }$
in §4.2, one can easily check that the restriction of
![]() $\unicode[STIX]{x1D703}_{m}^{\prime }$
to
$\unicode[STIX]{x1D703}_{m}^{\prime }$
to
![]() $K_{J^{\prime }}^{\prime }$
is zero. Thus the restriction of the
$K_{J^{\prime }}^{\prime }$
is zero. Thus the restriction of the
![]() $\mathbb{G}_{m}$
-gerbe
$\mathbb{G}_{m}$
-gerbe
![]() $\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })$
to
$\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })$
to
![]() $K_{J^{\prime }}^{\prime }$
is canonical trivial and we can regard the structure sheaf
$K_{J^{\prime }}^{\prime }$
is canonical trivial and we can regard the structure sheaf
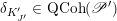 $\unicode[STIX]{x1D6FF}_{K_{J^{\prime }}^{\prime }}\in \operatorname{QCoh}(\mathscr{P}^{\prime })$
as an object in
$\unicode[STIX]{x1D6FF}_{K_{J^{\prime }}^{\prime }}\in \operatorname{QCoh}(\mathscr{P}^{\prime })$
as an object in
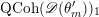 $\operatorname{QCoh}(\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime }))_{1}$
. Let
$\operatorname{QCoh}(\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime }))_{1}$
. Let
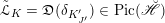 $\tilde{{\mathcal{L}}}_{K}=\mathfrak{D}(\unicode[STIX]{x1D6FF}_{K_{J^{\prime }}^{\prime }})\in \operatorname{Pic}(\breve{\mathscr{H}})$
be the image of
$\tilde{{\mathcal{L}}}_{K}=\mathfrak{D}(\unicode[STIX]{x1D6FF}_{K_{J^{\prime }}^{\prime }})\in \operatorname{Pic}(\breve{\mathscr{H}})$
be the image of
![]() $\unicode[STIX]{x1D6FF}_{K_{J^{\prime }}^{\prime }}$
under the twisted duality
$\unicode[STIX]{x1D6FF}_{K_{J^{\prime }}^{\prime }}$
under the twisted duality
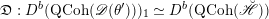 $\mathfrak{D}:D^{b}(\operatorname{QCoh}(\mathscr{D}(\unicode[STIX]{x1D703}^{\prime })))_{1}\simeq D^{b}(\operatorname{QCoh}(\breve{\mathscr{H}}))$
.
$\mathfrak{D}:D^{b}(\operatorname{QCoh}(\mathscr{D}(\unicode[STIX]{x1D703}^{\prime })))_{1}\simeq D^{b}(\operatorname{QCoh}(\breve{\mathscr{H}}))$
.
Lemma 5.6.4. We have
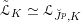 $\tilde{{\mathcal{L}}}_{K}\simeq {\mathcal{L}}_{\breve{J}^{p},K}$
.
$\tilde{{\mathcal{L}}}_{K}\simeq {\mathcal{L}}_{\breve{J}^{p},K}$
.
Proof. Let
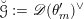 $\breve{{\mathcal{G}}}:=\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })^{\vee }$
. We have a short exact sequence of Beilinson
$\breve{{\mathcal{G}}}:=\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })^{\vee }$
. We have a short exact sequence of Beilinson
![]() $1$
-motives
$1$
-motives
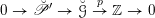 $0\rightarrow \breve{\mathscr{P}}^{\prime }\rightarrow \breve{{\mathcal{G}}}\stackrel{p}{\rightarrow }\mathbb{Z}\rightarrow 0$
and
$0\rightarrow \breve{\mathscr{P}}^{\prime }\rightarrow \breve{{\mathcal{G}}}\stackrel{p}{\rightarrow }\mathbb{Z}\rightarrow 0$
and
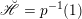 $\breve{\mathscr{H}}=p^{-1}(1)$
. The construction of duality for torsors in §A.7 implies that there is a multiplicative line bundle
$\breve{\mathscr{H}}=p^{-1}(1)$
. The construction of duality for torsors in §A.7 implies that there is a multiplicative line bundle
![]() $\tilde{{\mathcal{L}}}_{\breve{{\mathcal{G}}},K}$
on
$\tilde{{\mathcal{L}}}_{\breve{{\mathcal{G}}},K}$
on
![]() $\breve{{\mathcal{G}}}$
such that
$\breve{{\mathcal{G}}}$
such that
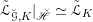 $\tilde{{\mathcal{L}}}_{\breve{{\mathcal{G}}},K}|_{\breve{\mathscr{H}}}\simeq \tilde{{\mathcal{L}}}_{K}$
. Moreover, this line bundle is characterized by the property that
$\tilde{{\mathcal{L}}}_{\breve{{\mathcal{G}}},K}|_{\breve{\mathscr{H}}}\simeq \tilde{{\mathcal{L}}}_{K}$
. Moreover, this line bundle is characterized by the property that
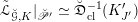 $\tilde{{\mathcal{L}}}_{\breve{{\mathcal{G}}},K}|_{\breve{\mathscr{P}}^{\prime }}\simeq \breve{\mathfrak{D}}_{\text{cl}}^{-1}(K_{J^{\prime }}^{\prime })$
. Observe that we have a natural map
$\tilde{{\mathcal{L}}}_{\breve{{\mathcal{G}}},K}|_{\breve{\mathscr{P}}^{\prime }}\simeq \breve{\mathfrak{D}}_{\text{cl}}^{-1}(K_{J^{\prime }}^{\prime })$
. Observe that we have a natural map
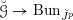 $\breve{{\mathcal{G}}}\rightarrow \operatorname{Bun}_{\breve{J}^{p}}$
of Picard stacksFootnote
8
such that the composition
$\breve{{\mathcal{G}}}\rightarrow \operatorname{Bun}_{\breve{J}^{p}}$
of Picard stacksFootnote
8
such that the composition
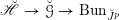 $\breve{\mathscr{H}}\rightarrow \breve{{\mathcal{G}}}\rightarrow \operatorname{Bun}_{\breve{J}^{p}}$
is the natural inclusion. Thus the morphism
$\breve{\mathscr{H}}\rightarrow \breve{{\mathcal{G}}}\rightarrow \operatorname{Bun}_{\breve{J}^{p}}$
is the natural inclusion. Thus the morphism
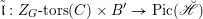 $\tilde{\mathfrak{l}}:Z_{G}\text{-}\text{tors}(C)\times B^{\prime }\rightarrow \operatorname{Pic}(\breve{\mathscr{H}})$
factors through a morphism
$\tilde{\mathfrak{l}}:Z_{G}\text{-}\text{tors}(C)\times B^{\prime }\rightarrow \operatorname{Pic}(\breve{\mathscr{H}})$
factors through a morphism
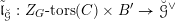 $\tilde{\mathfrak{l}}_{\breve{{\mathcal{G}}}}:Z_{G}\text{-}\text{tors}(C)\times B^{\prime }\rightarrow \breve{{\mathcal{G}}}^{\vee }$
, and the corresponding multiplicative line bundle
$\tilde{\mathfrak{l}}_{\breve{{\mathcal{G}}}}:Z_{G}\text{-}\text{tors}(C)\times B^{\prime }\rightarrow \breve{{\mathcal{G}}}^{\vee }$
, and the corresponding multiplicative line bundle
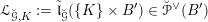 ${\mathcal{L}}_{\breve{{\mathcal{G}}},K}:=\tilde{\mathfrak{l}}_{\breve{{\mathcal{G}}}}(\{K\}\times B^{\prime })\in \breve{{\mathcal{P}}}^{\vee }(B^{\prime })$
satisfies
${\mathcal{L}}_{\breve{{\mathcal{G}}},K}:=\tilde{\mathfrak{l}}_{\breve{{\mathcal{G}}}}(\{K\}\times B^{\prime })\in \breve{{\mathcal{P}}}^{\vee }(B^{\prime })$
satisfies
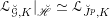 ${\mathcal{L}}_{\breve{{\mathcal{G}}},K}|_{\breve{\mathscr{H}}}\simeq {\mathcal{L}}_{\breve{J}^{p},K}$
. It is enough to show that
${\mathcal{L}}_{\breve{{\mathcal{G}}},K}|_{\breve{\mathscr{H}}}\simeq {\mathcal{L}}_{\breve{J}^{p},K}$
. It is enough to show that
 $\tilde{{\mathcal{L}}}_{\breve{{\mathcal{G}}},K}\simeq {\mathcal{L}}_{\breve{{\mathcal{G}}},K}$
. From the characterization of
$\tilde{{\mathcal{L}}}_{\breve{{\mathcal{G}}},K}\simeq {\mathcal{L}}_{\breve{{\mathcal{G}}},K}$
. From the characterization of
![]() $\tilde{{\mathcal{L}}}_{\breve{{\mathcal{G}}},K}$
, it is enough to show that
$\tilde{{\mathcal{L}}}_{\breve{{\mathcal{G}}},K}$
, it is enough to show that
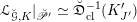 ${\mathcal{L}}_{\breve{{\mathcal{G}}},K}|_{\breve{\mathscr{P}}^{\prime }}\simeq \breve{\mathfrak{D}}_{\text{cl}}^{-1}(K_{J^{\prime }}^{\prime })$
. But this follows from Proposition 3.7.4 and the fact that
${\mathcal{L}}_{\breve{{\mathcal{G}}},K}|_{\breve{\mathscr{P}}^{\prime }}\simeq \breve{\mathfrak{D}}_{\text{cl}}^{-1}(K_{J^{\prime }}^{\prime })$
. But this follows from Proposition 3.7.4 and the fact that
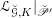 ${\mathcal{L}}_{\breve{{\mathcal{G}}},K}|_{\breve{\mathscr{P}}^{\prime }}$
is isomorphic to
${\mathcal{L}}_{\breve{{\mathcal{G}}},K}|_{\breve{\mathscr{P}}^{\prime }}$
is isomorphic to
![]() ${\mathcal{L}}_{\breve{J}^{\prime },K^{\prime }}$
.◻
${\mathcal{L}}_{\breve{J}^{\prime },K^{\prime }}$
.◻
Recall that a choice of
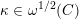 $\unicode[STIX]{x1D705}\in \unicode[STIX]{x1D714}^{1/2}(C)$
defines an isomorphism
$\unicode[STIX]{x1D705}\in \unicode[STIX]{x1D714}^{1/2}(C)$
defines an isomorphism
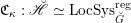 $\mathfrak{C}_{\unicode[STIX]{x1D705}}:\breve{\mathscr{H}}\simeq \operatorname{LocSys}_{\breve{G}}^{\text{reg}}$
. More precisely, we have
$\mathfrak{C}_{\unicode[STIX]{x1D705}}:\breve{\mathscr{H}}\simeq \operatorname{LocSys}_{\breve{G}}^{\text{reg}}$
. More precisely, we have
 $\mathfrak{C}_{\unicode[STIX]{x1D705}}(P,\unicode[STIX]{x1D6FB})=(P\otimes F_{C}^{\ast }E_{\unicode[STIX]{x1D705}^{\prime }},\unicode[STIX]{x1D6FB}_{P\otimes F_{C}^{\ast }E_{\unicode[STIX]{x1D705}^{\prime }}})$
where
$\mathfrak{C}_{\unicode[STIX]{x1D705}}(P,\unicode[STIX]{x1D6FB})=(P\otimes F_{C}^{\ast }E_{\unicode[STIX]{x1D705}^{\prime }},\unicode[STIX]{x1D6FB}_{P\otimes F_{C}^{\ast }E_{\unicode[STIX]{x1D705}^{\prime }}})$
where
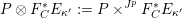 $P\otimes F_{C}^{\ast }E_{\unicode[STIX]{x1D705}^{\prime }}:=P\times ^{J^{p}}F_{C}^{\ast }E_{\unicode[STIX]{x1D705}^{\prime }}$
and
$P\otimes F_{C}^{\ast }E_{\unicode[STIX]{x1D705}^{\prime }}:=P\times ^{J^{p}}F_{C}^{\ast }E_{\unicode[STIX]{x1D705}^{\prime }}$
and
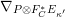 $\unicode[STIX]{x1D6FB}_{P\otimes F_{C}^{\ast }E_{\unicode[STIX]{x1D705}^{\prime }}}$
is the product connection.
$\unicode[STIX]{x1D6FB}_{P\otimes F_{C}^{\ast }E_{\unicode[STIX]{x1D705}^{\prime }}}$
is the product connection.
Lemma 5.6.5. The pullback of the line bundle
![]() ${\mathcal{L}}_{\breve{G},K}$
along the map
${\mathcal{L}}_{\breve{G},K}$
along the map
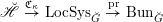 $\breve{\mathscr{H}}\stackrel{\mathfrak{C}_{\unicode[STIX]{x1D705}}}{\rightarrow }\operatorname{LocSys}_{\breve{G}}\stackrel{\operatorname{pr}}{\rightarrow }\operatorname{Bun}_{\breve{G}}$
is isomorphic to
$\breve{\mathscr{H}}\stackrel{\mathfrak{C}_{\unicode[STIX]{x1D705}}}{\rightarrow }\operatorname{LocSys}_{\breve{G}}\stackrel{\operatorname{pr}}{\rightarrow }\operatorname{Bun}_{\breve{G}}$
is isomorphic to
![]() $\tilde{{\mathcal{L}}}_{K}$
. That is, we have
$\tilde{{\mathcal{L}}}_{K}$
. That is, we have
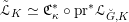 $\tilde{{\mathcal{L}}}_{K}\simeq \mathfrak{C}_{\unicode[STIX]{x1D705}}^{\ast }\circ \operatorname{pr}^{\ast }{\mathcal{L}}_{\breve{G},K}$
.
$\tilde{{\mathcal{L}}}_{K}\simeq \mathfrak{C}_{\unicode[STIX]{x1D705}}^{\ast }\circ \operatorname{pr}^{\ast }{\mathcal{L}}_{\breve{G},K}$
.
Proof. The proof is similar to the proof of Lemma 3.7.2. Recall that the line bundles
![]() ${\mathcal{L}}_{\breve{G},K}$
and
${\mathcal{L}}_{\breve{G},K}$
and
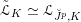 $\tilde{{\mathcal{L}}}_{K}\simeq {\mathcal{L}}_{\breve{J}^{p},K}$
are induced by the generalized Chern class map
$\tilde{{\mathcal{L}}}_{K}\simeq {\mathcal{L}}_{\breve{J}^{p},K}$
are induced by the generalized Chern class map
![]() $\tilde{c}_{\breve{G}}$
,
$\tilde{c}_{\breve{G}}$
,
![]() $\tilde{c}_{\breve{J}^{p}}$
. Therefore it is enough to show that for any
$\tilde{c}_{\breve{J}^{p}}$
. Therefore it is enough to show that for any
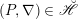 $(P,\unicode[STIX]{x1D6FB})\in \breve{\mathscr{H}}$
there is a canonical isomorphism
$(P,\unicode[STIX]{x1D6FB})\in \breve{\mathscr{H}}$
there is a canonical isomorphism
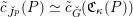 $\tilde{c}_{\breve{J}^{p}}(P)\simeq \tilde{c}_{\breve{G}}(\mathfrak{C}_{\unicode[STIX]{x1D705}}(P))$
of
$\tilde{c}_{\breve{J}^{p}}(P)\simeq \tilde{c}_{\breve{G}}(\mathfrak{C}_{\unicode[STIX]{x1D705}}(P))$
of
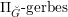 $\unicode[STIX]{x1D6F1}_{\breve{G}}\text{-}\text{gerbes}$
, where
$\unicode[STIX]{x1D6F1}_{\breve{G}}\text{-}\text{gerbes}$
, where
 $\mathfrak{C}_{\unicode[STIX]{x1D705}}(P)=P\times ^{J^{p}}F_{C}^{\ast }E_{\unicode[STIX]{x1D705}^{\prime }}$
. Let
$\mathfrak{C}_{\unicode[STIX]{x1D705}}(P)=P\times ^{J^{p}}F_{C}^{\ast }E_{\unicode[STIX]{x1D705}^{\prime }}$
. Let
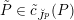 $\tilde{P}\in \tilde{c}_{\breve{J}^{p}}(P)$
and
$\tilde{P}\in \tilde{c}_{\breve{J}^{p}}(P)$
and
![]() $\tilde{E}_{\unicode[STIX]{x1D705}^{\prime }}$
be the canonical lifting of the Kostant section appearing in Lemma 3.7.2. The
$\tilde{E}_{\unicode[STIX]{x1D705}^{\prime }}$
be the canonical lifting of the Kostant section appearing in Lemma 3.7.2. The
![]() $G_{\text{sc}}$
-torsor
$G_{\text{sc}}$
-torsor
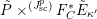 $\tilde{P}\times ^{(J_{\text{sc}}^{p})}F_{C}^{\ast }\tilde{E}_{\unicode[STIX]{x1D705}^{\prime }}$
is a lifting of
$\tilde{P}\times ^{(J_{\text{sc}}^{p})}F_{C}^{\ast }\tilde{E}_{\unicode[STIX]{x1D705}^{\prime }}$
is a lifting of
![]() $\mathfrak{C}_{\unicode[STIX]{x1D705}}(P)$
and the assignment
$\mathfrak{C}_{\unicode[STIX]{x1D705}}(P)$
and the assignment
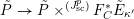 $\tilde{P}\rightarrow \tilde{P}\times ^{(J_{\text{sc}}^{p})}F_{C}^{\ast }\tilde{E}_{\unicode[STIX]{x1D705}^{\prime }}$
defines an isomorphism between
$\tilde{P}\rightarrow \tilde{P}\times ^{(J_{\text{sc}}^{p})}F_{C}^{\ast }\tilde{E}_{\unicode[STIX]{x1D705}^{\prime }}$
defines an isomorphism between
![]() $\tilde{c}_{J^{p}}(P)$
and
$\tilde{c}_{J^{p}}(P)$
and
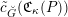 $\tilde{c}_{\breve{G}}(\mathfrak{C}_{\unicode[STIX]{x1D705}}(P))$
. This finishes the proof.◻
$\tilde{c}_{\breve{G}}(\mathfrak{C}_{\unicode[STIX]{x1D705}}(P))$
. This finishes the proof.◻
Now we prove Theorem 5.6.1. Recall that we have
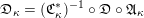 $\mathfrak{D}_{\unicode[STIX]{x1D705}}=(\mathfrak{C}_{\unicode[STIX]{x1D705}}^{\ast })^{-1}\circ \mathfrak{D}\circ \mathfrak{A}_{\unicode[STIX]{x1D705}}$
where
$\mathfrak{D}_{\unicode[STIX]{x1D705}}=(\mathfrak{C}_{\unicode[STIX]{x1D705}}^{\ast })^{-1}\circ \mathfrak{D}\circ \mathfrak{A}_{\unicode[STIX]{x1D705}}$
where
![]() $\mathfrak{A}_{\unicode[STIX]{x1D705}}$
and
$\mathfrak{A}_{\unicode[STIX]{x1D705}}$
and
![]() $\mathfrak{C}_{\unicode[STIX]{x1D705}}^{\ast }$
are equivalences constructed in §5.3. It follows from the definition that under the equivalence
$\mathfrak{C}_{\unicode[STIX]{x1D705}}^{\ast }$
are equivalences constructed in §5.3. It follows from the definition that under the equivalence
![]() $\mathfrak{C}_{\unicode[STIX]{x1D705}}^{\ast }$
the functor
$\mathfrak{C}_{\unicode[STIX]{x1D705}}^{\ast }$
the functor
![]() $b_{\breve{G},\unicode[STIX]{x1D712}}^{\ast }$
becomes the functor induced by the geometric action of
$b_{\breve{G},\unicode[STIX]{x1D712}}^{\ast }$
becomes the functor induced by the geometric action of
 $K_{\breve{G},\unicode[STIX]{x1D712}}^{\prime }\in Z(\breve{G})\text{-}\text{tors}(C^{\prime })$
on
$K_{\breve{G},\unicode[STIX]{x1D712}}^{\prime }\in Z(\breve{G})\text{-}\text{tors}(C^{\prime })$
on
![]() $\breve{\mathscr{H}}$
.Footnote
9
Now Theorem A.7.2 implies, under the equivalence
$\breve{\mathscr{H}}$
.Footnote
9
Now Theorem A.7.2 implies, under the equivalence
 $$\begin{eqnarray}\mathfrak{D}^{}:D^{b}(\operatorname{QCoh}(\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })|_{B^{^{\prime }0}}))_{1}\simeq D^{b}(\operatorname{QCoh}(\breve{\mathscr{H}}|_{B^{^{\prime }0}})),\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{D}^{}:D^{b}(\operatorname{QCoh}(\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })|_{B^{^{\prime }0}}))_{1}\simeq D^{b}(\operatorname{QCoh}(\breve{\mathscr{H}}|_{B^{^{\prime }0}})),\end{eqnarray}$$
the above geometric action becomes the functor of tensoring with the line bundle
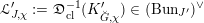 ${\mathcal{L}}_{J,\unicode[STIX]{x1D712}}^{\prime }:=\mathfrak{D}_{\text{cl}}^{-1}(K_{\breve{G},\unicode[STIX]{x1D712}}^{\prime })\in (\operatorname{Bun}_{J^{\prime }})^{\vee }$
.Footnote
10
By Lemmas 3.7.2 and 3.7.4, the line bundle
${\mathcal{L}}_{J,\unicode[STIX]{x1D712}}^{\prime }:=\mathfrak{D}_{\text{cl}}^{-1}(K_{\breve{G},\unicode[STIX]{x1D712}}^{\prime })\in (\operatorname{Bun}_{J^{\prime }})^{\vee }$
.Footnote
10
By Lemmas 3.7.2 and 3.7.4, the line bundle
![]() ${\mathcal{L}}_{J,\unicode[STIX]{x1D712}}^{\prime }$
is equal to the pullback of
${\mathcal{L}}_{J,\unicode[STIX]{x1D712}}^{\prime }$
is equal to the pullback of
![]() ${\mathcal{L}}_{G,\unicode[STIX]{x1D712}}^{\prime }$
under the map
${\mathcal{L}}_{G,\unicode[STIX]{x1D712}}^{\prime }$
under the map
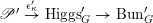 $\mathscr{P}^{\prime }\stackrel{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}}^{\prime }}{\rightarrow }\operatorname{Higgs}_{G}^{\prime }\rightarrow \operatorname{Bun}_{G}^{\prime }$
. On the other hand, since the equivalence
$\mathscr{P}^{\prime }\stackrel{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}}^{\prime }}{\rightarrow }\operatorname{Higgs}_{G}^{\prime }\rightarrow \operatorname{Bun}_{G}^{\prime }$
. On the other hand, since the equivalence
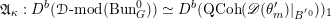 $\mathfrak{A}_{\unicode[STIX]{x1D705}}:D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G}^{0}))\simeq D^{b}(\operatorname{QCoh}(\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })|_{B^{^{\prime }0}}))_{1}$
is induced by pullback along the morphism
$\mathfrak{A}_{\unicode[STIX]{x1D705}}:D^{b}({\mathcal{D}}\text{-}\text{mod}(\operatorname{Bun}_{G}^{0}))\simeq D^{b}(\operatorname{QCoh}(\mathscr{D}(\unicode[STIX]{x1D703}_{m}^{\prime })|_{B^{^{\prime }0}}))_{1}$
is induced by pullback along the morphism
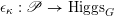 $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}}:\mathscr{P}\rightarrow \operatorname{Higgs}_{G}$
, an easy exercise shows that under the equivalence
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}}:\mathscr{P}\rightarrow \operatorname{Higgs}_{G}$
, an easy exercise shows that under the equivalence
![]() $\mathfrak{A}_{\unicode[STIX]{x1D705}}$
the functor of tensoring with
$\mathfrak{A}_{\unicode[STIX]{x1D705}}$
the functor of tensoring with
![]() ${\mathcal{L}}_{J,\unicode[STIX]{x1D712}}^{\prime }$
becomes the functor of tensoring with
${\mathcal{L}}_{J,\unicode[STIX]{x1D712}}^{\prime }$
becomes the functor of tensoring with
![]() ${\mathcal{L}}_{G,\unicode[STIX]{x1D712}}$
. This implies part (1) of Theorem 5.6.1.
${\mathcal{L}}_{G,\unicode[STIX]{x1D712}}$
. This implies part (1) of Theorem 5.6.1.
The proof of part (2) of Theorem 5.6.1 is similar to part (1). Unraveling the definition of
![]() $a_{G,\unicode[STIX]{x1D712}}^{\ast }$
and the construction of
$a_{G,\unicode[STIX]{x1D712}}^{\ast }$
and the construction of
![]() $\mathfrak{A}_{\unicode[STIX]{x1D705}}$
, one sees that
$\mathfrak{A}_{\unicode[STIX]{x1D705}}$
, one sees that
![]() $\mathfrak{A}_{\unicode[STIX]{x1D705}}$
interchanges the functor
$\mathfrak{A}_{\unicode[STIX]{x1D705}}$
interchanges the functor
![]() $a_{G,\unicode[STIX]{x1D712}}^{\ast }$
with the functor of convolution product with
$a_{G,\unicode[STIX]{x1D712}}^{\ast }$
with the functor of convolution product with
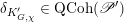 $\unicode[STIX]{x1D6FF}_{K_{G,\unicode[STIX]{x1D712}}^{\prime }}\in \operatorname{QCoh}(\mathscr{P}^{\prime })$
. Now Theorem A.7.2 implies that, under the equivalence
$\unicode[STIX]{x1D6FF}_{K_{G,\unicode[STIX]{x1D712}}^{\prime }}\in \operatorname{QCoh}(\mathscr{P}^{\prime })$
. Now Theorem A.7.2 implies that, under the equivalence
![]() $\mathfrak{D}$
, the above convolution action becomes the functor of tensoring with the line bundle
$\mathfrak{D}$
, the above convolution action becomes the functor of tensoring with the line bundle
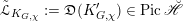 $\tilde{{\mathcal{L}}}_{K_{G,\unicode[STIX]{x1D712}}}:=\mathfrak{D}(K_{G,\unicode[STIX]{x1D712}}^{\prime })\in \operatorname{Pic}\breve{\mathscr{H}}$
. By Lemmas 5.6.4 and 5.6.5, the line bundle
$\tilde{{\mathcal{L}}}_{K_{G,\unicode[STIX]{x1D712}}}:=\mathfrak{D}(K_{G,\unicode[STIX]{x1D712}}^{\prime })\in \operatorname{Pic}\breve{\mathscr{H}}$
. By Lemmas 5.6.4 and 5.6.5, the line bundle
![]() $\tilde{{\mathcal{L}}}_{K_{G,\unicode[STIX]{x1D712}}}$
is isomorphic to the pullback of
$\tilde{{\mathcal{L}}}_{K_{G,\unicode[STIX]{x1D712}}}$
is isomorphic to the pullback of
![]() ${\mathcal{L}}_{\breve{G},\unicode[STIX]{x1D712}}$
under the map
${\mathcal{L}}_{\breve{G},\unicode[STIX]{x1D712}}$
under the map
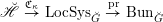 $\breve{\mathscr{H}}\stackrel{\mathfrak{C}_{\unicode[STIX]{x1D705}}}{\rightarrow }\operatorname{LocSys}_{\breve{G}}\stackrel{\operatorname{pr}}{\rightarrow }\operatorname{Bun}_{\breve{G}}$
. It implies that
$\breve{\mathscr{H}}\stackrel{\mathfrak{C}_{\unicode[STIX]{x1D705}}}{\rightarrow }\operatorname{LocSys}_{\breve{G}}\stackrel{\operatorname{pr}}{\rightarrow }\operatorname{Bun}_{\breve{G}}$
. It implies that
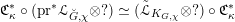 $\mathfrak{C}_{\unicode[STIX]{x1D705}}^{\ast }\circ (\operatorname{pr}^{\ast }{\mathcal{L}}_{\breve{G},\unicode[STIX]{x1D712}}\otimes ?)\simeq (\tilde{{\mathcal{L}}}_{K_{G,\unicode[STIX]{x1D712}}}\otimes ?)\circ \mathfrak{C}_{\unicode[STIX]{x1D705}}^{\ast }$
.
$\mathfrak{C}_{\unicode[STIX]{x1D705}}^{\ast }\circ (\operatorname{pr}^{\ast }{\mathcal{L}}_{\breve{G},\unicode[STIX]{x1D712}}\otimes ?)\simeq (\tilde{{\mathcal{L}}}_{K_{G,\unicode[STIX]{x1D712}}}\otimes ?)\circ \mathfrak{C}_{\unicode[STIX]{x1D705}}^{\ast }$
.
Acknowledgements
We thank Roman Bezrukavnikov, Roman Travkin and Zhiwei Yun for useful discussions, and Uwe Weselmann for helpful comments and suggestions. The first author would like to thank his advisor Roman Bezrukavnikov for continuous interest in this work and for much helpful advice. T.-H. Chen is partially supported by NSF under the agreement no. DMS-1128155. X. Zhu is partially supported by NSF grants DMS-1001280/1313894 and DMS-1303296 and an AMS Centennial Fellowship.
Appendix A Beilinson 1-motive
In this section, we review the duality theory of Beilinson
![]() $1$
-motives. The main references are [Reference ArinkinAri08, Reference Donagi and PantevDP12, Reference Donagi and PantevDP08, Reference LaumonLau96].
$1$
-motives. The main references are [Reference ArinkinAri08, Reference Donagi and PantevDP12, Reference Donagi and PantevDP08, Reference LaumonLau96].
A.1 Picard stack
Let us first review the theory of Picard stacks. The standard reference is [Reference DeligneDel73, §1.4]. Let
![]() ${\mathcal{T}}$
be a given site. Recall that a Picard Stack is a stack
${\mathcal{T}}$
be a given site. Recall that a Picard Stack is a stack
![]() $\mathscr{P}$
over
$\mathscr{P}$
over
![]() ${\mathcal{T}}$
together with a bi-functor
${\mathcal{T}}$
together with a bi-functor
 $$\begin{eqnarray}\otimes :\mathscr{P}\times \mathscr{P}\rightarrow \mathscr{P},\end{eqnarray}$$
$$\begin{eqnarray}\otimes :\mathscr{P}\times \mathscr{P}\rightarrow \mathscr{P},\end{eqnarray}$$
and the associativity and commutative constraints
 $$\begin{eqnarray}a:\otimes \circ (\otimes \times 1)\simeq \otimes \circ (1\times \otimes ),\quad c:\otimes \simeq \otimes \circ \text{flip},\end{eqnarray}$$
$$\begin{eqnarray}a:\otimes \circ (\otimes \times 1)\simeq \otimes \circ (1\times \otimes ),\quad c:\otimes \simeq \otimes \circ \text{flip},\end{eqnarray}$$
such that for every
![]() $U\in {\mathcal{T}}$
,
$U\in {\mathcal{T}}$
,
![]() $\mathscr{P}(U)$
form a Picard groupoid (i.e., symmetrical monoidal groupoid such that every object has a monoidal inverse). The Picard stack is called strictly commutative if
$\mathscr{P}(U)$
form a Picard groupoid (i.e., symmetrical monoidal groupoid such that every object has a monoidal inverse). The Picard stack is called strictly commutative if
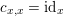 $c_{x,x}=\operatorname{id}_{x}$
for every
$c_{x,x}=\operatorname{id}_{x}$
for every
![]() $x\in \mathscr{P}$
. In the paper, Picard stacks will always mean strictly commutative ones.
$x\in \mathscr{P}$
. In the paper, Picard stacks will always mean strictly commutative ones.
Let us denote by
![]() ${\mathcal{P}}{\mathcal{S}}/{\mathcal{T}}$
the 2-category of Picard stacks over
${\mathcal{P}}{\mathcal{S}}/{\mathcal{T}}$
the 2-category of Picard stacks over
![]() ${\mathcal{T}}$
. This means that if
${\mathcal{T}}$
. This means that if
![]() $\mathscr{P}_{1},\mathscr{P}_{2}$
are two Picard stacks over
$\mathscr{P}_{1},\mathscr{P}_{2}$
are two Picard stacks over
![]() ${\mathcal{T}}$
,
${\mathcal{T}}$
,
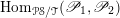 $\operatorname{Hom}_{{\mathcal{P}}{\mathcal{S}}/{\mathcal{T}}}(\mathscr{P}_{1},\mathscr{P}_{2})$
form a category. Indeed,
$\operatorname{Hom}_{{\mathcal{P}}{\mathcal{S}}/{\mathcal{T}}}(\mathscr{P}_{1},\mathscr{P}_{2})$
form a category. Indeed,
![]() ${\mathcal{P}}{\mathcal{S}}/{\mathcal{T}}$
is canonically enriched over itself. For
${\mathcal{P}}{\mathcal{S}}/{\mathcal{T}}$
is canonically enriched over itself. For
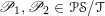 $\mathscr{P}_{1},\mathscr{P}_{2}\in {\mathcal{P}}{\mathcal{S}}/{\mathcal{T}}$
, we use
$\mathscr{P}_{1},\mathscr{P}_{2}\in {\mathcal{P}}{\mathcal{S}}/{\mathcal{T}}$
, we use
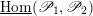 $\text{}\underline{\operatorname{Hom}}(\mathscr{P}_{1},\mathscr{P}_{2})$
to denote the Picard stack of 1-homomorphisms from
$\text{}\underline{\operatorname{Hom}}(\mathscr{P}_{1},\mathscr{P}_{2})$
to denote the Picard stack of 1-homomorphisms from
![]() $\mathscr{P}_{1}$
to
$\mathscr{P}_{1}$
to
![]() $\mathscr{P}_{2}$
over
$\mathscr{P}_{2}$
over
![]() ${\mathcal{T}}$
(cf. [Reference DeligneDel73, §1.4.7]). On the other hand, let
${\mathcal{T}}$
(cf. [Reference DeligneDel73, §1.4.7]). On the other hand, let
![]() $C^{[-1,0]}$
be the 2-category of 2-term complexes of sheaves of abelian groups
$C^{[-1,0]}$
be the 2-category of 2-term complexes of sheaves of abelian groups
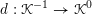 $d:{\mathcal{K}}^{-1}\rightarrow {\mathcal{K}}^{0}$
with
$d:{\mathcal{K}}^{-1}\rightarrow {\mathcal{K}}^{0}$
with
![]() ${\mathcal{K}}^{-1}$
injective and 1-morphisms are morphisms of chain complexes (and 2-morphisms are homotopy of chain complexes).Footnote
11
Let
${\mathcal{K}}^{-1}$
injective and 1-morphisms are morphisms of chain complexes (and 2-morphisms are homotopy of chain complexes).Footnote
11
Let
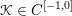 ${\mathcal{K}}\in C^{[-1,0]}$
. We associate to it a Picard prestack
${\mathcal{K}}\in C^{[-1,0]}$
. We associate to it a Picard prestack
![]() $\text{pch}({\mathcal{K}})$
whose
$\text{pch}({\mathcal{K}})$
whose
![]() $U$
point is the following Picard category.
$U$
point is the following Picard category.
-
(1) Objects of
 $\text{pch}({\mathcal{K}})(U)$
are equal to
$\text{pch}({\mathcal{K}})(U)$
are equal to
 ${\mathcal{K}}^{0}(U)$
.
${\mathcal{K}}^{0}(U)$
. -
(2) If
 $x,y\in {\mathcal{K}}^{0}(U)$
, a morphism from
$x,y\in {\mathcal{K}}^{0}(U)$
, a morphism from
 $x$
to
$x$
to
 $y$
is an element
$y$
is an element
 $f\in {\mathcal{K}}^{-1}(U)$
such that
$f\in {\mathcal{K}}^{-1}(U)$
such that
 $df=y-x$
.
$df=y-x$
.
Let
![]() $\text{ch}({\mathcal{K}})$
be the stackification of
$\text{ch}({\mathcal{K}})$
be the stackification of
![]() $\text{pch}({\mathcal{K}})$
. Then a theorem of Deligne (cf. [Reference DeligneDel73, Corollaire 1.4.17]) says that the functor
$\text{pch}({\mathcal{K}})$
. Then a theorem of Deligne (cf. [Reference DeligneDel73, Corollaire 1.4.17]) says that the functor
 $$\begin{eqnarray}\text{ch : C}^{[-1,0]}\rightarrow {\mathcal{P}}{\mathcal{S}}/{\mathcal{T}}\end{eqnarray}$$
$$\begin{eqnarray}\text{ch : C}^{[-1,0]}\rightarrow {\mathcal{P}}{\mathcal{S}}/{\mathcal{T}}\end{eqnarray}$$
is an equivalence of 2-categories.
Let us fix an inverse functor
![]() $(\,)^{\flat }$
of the above equivalence. So for
$(\,)^{\flat }$
of the above equivalence. So for
![]() $\mathscr{P}$
a Picard stack, we have a 2-term complex of sheaves of abelian groups
$\mathscr{P}$
a Picard stack, we have a 2-term complex of sheaves of abelian groups
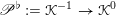 $\mathscr{P}^{\flat }:={\mathcal{K}}^{-1}\rightarrow {\mathcal{K}}^{0}$
. For example, if
$\mathscr{P}^{\flat }:={\mathcal{K}}^{-1}\rightarrow {\mathcal{K}}^{0}$
. For example, if
![]() $A$
is an abelian group in
$A$
is an abelian group in
![]() ${\mathcal{T}}$
, then its classifying stack
${\mathcal{T}}$
, then its classifying stack
![]() $BA$
is a natural Picard stack and
$BA$
is a natural Picard stack and
![]() $(BA)^{\flat }$
can be represented by a 2-term complex quasi-isomorphic to
$(BA)^{\flat }$
can be represented by a 2-term complex quasi-isomorphic to
![]() $A[1]$
. The following result of Deligne (cf. [Reference DeligneDel73, Construction 1.4.18]) is convenient for computations:
$A[1]$
. The following result of Deligne (cf. [Reference DeligneDel73, Construction 1.4.18]) is convenient for computations:
 $$\begin{eqnarray}(\text{}\underline{\operatorname{Hom}}(\mathscr{P}_{1},\mathscr{P}_{2}))^{\flat }\simeq \unicode[STIX]{x1D70F}_{{\leqslant}0}\operatorname{R}\text{}\underline{\operatorname{Hom}}(\mathscr{P}_{1}^{\flat },\mathscr{P}_{2}^{\flat }).\end{eqnarray}$$
$$\begin{eqnarray}(\text{}\underline{\operatorname{Hom}}(\mathscr{P}_{1},\mathscr{P}_{2}))^{\flat }\simeq \unicode[STIX]{x1D70F}_{{\leqslant}0}\operatorname{R}\text{}\underline{\operatorname{Hom}}(\mathscr{P}_{1}^{\flat },\mathscr{P}_{2}^{\flat }).\end{eqnarray}$$
A.2 Short exact sequences of Picard stacks
Let
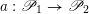 $a:\mathscr{P}_{1}\rightarrow \mathscr{P}_{2}$
be a homomorphism of Picard stacks. We define
$a:\mathscr{P}_{1}\rightarrow \mathscr{P}_{2}$
be a homomorphism of Picard stacks. We define
![]() $\ker (a)$
as the fiber
$\ker (a)$
as the fiber
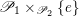 $\mathscr{P}_{1}\times _{\mathscr{P}_{2}}\{e\}$
, where
$\mathscr{P}_{1}\times _{\mathscr{P}_{2}}\{e\}$
, where
![]() $e\in \mathscr{P}_{2}$
is the unit. Then
$e\in \mathscr{P}_{2}$
is the unit. Then
![]() $\ker (a)$
acquires a natural Picard stack structure. The next lemma follows from the construction of
$\ker (a)$
acquires a natural Picard stack structure. The next lemma follows from the construction of
![]() $\text{ch}$
.
$\text{ch}$
.
Lemma A.2.1. There is a natural isomorphism
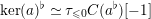 $\ker (a)^{\flat }\simeq \unicode[STIX]{x1D70F}_{{\leqslant}0}C(a^{\flat })[-1]$
, where
$\ker (a)^{\flat }\simeq \unicode[STIX]{x1D70F}_{{\leqslant}0}C(a^{\flat })[-1]$
, where
![]() $C(a^{\flat })$
is the cone of the morphism of complexes
$C(a^{\flat })$
is the cone of the morphism of complexes
 $$\begin{eqnarray}a^{\flat }:\mathscr{P}_{1}^{\flat }\rightarrow \mathscr{P}_{2}^{\flat }.\end{eqnarray}$$
$$\begin{eqnarray}a^{\flat }:\mathscr{P}_{1}^{\flat }\rightarrow \mathscr{P}_{2}^{\flat }.\end{eqnarray}$$
A left exact sequence of Picard stacks, usually denoted by
 $$\begin{eqnarray}1\rightarrow \mathscr{P}_{1}\stackrel{a}{\rightarrow }\mathscr{P}_{2}\stackrel{b}{\rightarrow }\mathscr{P}_{3},\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow \mathscr{P}_{1}\stackrel{a}{\rightarrow }\mathscr{P}_{2}\stackrel{b}{\rightarrow }\mathscr{P}_{3},\end{eqnarray}$$
is a sequence of homomorphisms of Picard stacks that exhibits
![]() $\mathscr{P}_{1}$
as
$\mathscr{P}_{1}$
as
![]() $\ker (b)$
. If, in addition locally on
$\ker (b)$
. If, in addition locally on
![]() ${\mathcal{T}}$
,
${\mathcal{T}}$
,
![]() $b$
is essentially surjective, we call such a sequence exact and denote it by
$b$
is essentially surjective, we call such a sequence exact and denote it by
 $$\begin{eqnarray}1\rightarrow \mathscr{P}_{1}\stackrel{a}{\rightarrow }\mathscr{P}_{2}\stackrel{b}{\rightarrow }\mathscr{P}_{3}\rightarrow 1.\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow \mathscr{P}_{1}\stackrel{a}{\rightarrow }\mathscr{P}_{2}\stackrel{b}{\rightarrow }\mathscr{P}_{3}\rightarrow 1.\end{eqnarray}$$
Sometimes, we also call
![]() $\mathscr{P}_{2}$
an extension of
$\mathscr{P}_{2}$
an extension of
![]() $\mathscr{P}_{3}$
by
$\mathscr{P}_{3}$
by
![]() $\mathscr{P}_{1}$
. The following lemma is used in several places in the paper.
$\mathscr{P}_{1}$
. The following lemma is used in several places in the paper.
Lemma A.2.2. The sequence of homomorphisms
 $\mathscr{P}_{1}\rightarrow \mathscr{P}_{2}\rightarrow \mathscr{P}_{3}$
is exact if and only if
$\mathscr{P}_{1}\rightarrow \mathscr{P}_{2}\rightarrow \mathscr{P}_{3}$
is exact if and only if
 $$\begin{eqnarray}\mathscr{P}_{1}^{\flat }\rightarrow \mathscr{P}_{2}^{\flat }\rightarrow \mathscr{P}_{3}^{\flat }\rightarrow\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{P}_{1}^{\flat }\rightarrow \mathscr{P}_{2}^{\flat }\rightarrow \mathscr{P}_{3}^{\flat }\rightarrow\end{eqnarray}$$
is a distinguished triangle.
A.3 Duality of Picard stacks
Let
![]() $S$
be a Noetherian scheme. We consider the category
$S$
be a Noetherian scheme. We consider the category
![]() $\text{Sch}/S$
of schemes over
$\text{Sch}/S$
of schemes over
![]() $S$
. We will endow
$S$
. We will endow
![]() $\text{Sch}/S$
with fpqc topology in the following discussion.
$\text{Sch}/S$
with fpqc topology in the following discussion.
Definition A.3.1. For a Picard stack
![]() $\mathscr{P}$
, we define the dual Picard stack as
$\mathscr{P}$
, we define the dual Picard stack as
 $$\begin{eqnarray}\mathscr{P}^{\vee }:=\text{}\underline{\text{Hom}}(\mathscr{P},B\mathbb{G}_{m}).\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{P}^{\vee }:=\text{}\underline{\text{Hom}}(\mathscr{P},B\mathbb{G}_{m}).\end{eqnarray}$$
Example A.3.2. Let
![]() $A\rightarrow S$
be an abelian scheme over
$A\rightarrow S$
be an abelian scheme over
![]() $S$
. Then by definition
$S$
. Then by definition
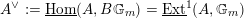 $A^{\vee }:=\text{}\underline{\text{Hom}}(A,B\mathbb{G}_{m})=\text{}\underline{\text{Ext}}^{1}(A,\mathbb{G}_{m})$
classifies the multiplicative line bundles on
$A^{\vee }:=\text{}\underline{\text{Hom}}(A,B\mathbb{G}_{m})=\text{}\underline{\text{Ext}}^{1}(A,\mathbb{G}_{m})$
classifies the multiplicative line bundles on
![]() $A$
, is represented by an abelian scheme over
$A$
, is represented by an abelian scheme over
![]() $S$
, called the dual abelian scheme of
$S$
, called the dual abelian scheme of
![]() $A$
.
$A$
.
Example A.3.3. Let
![]() $\unicode[STIX]{x1D6E4}$
be a finitely generated abelian group over
$\unicode[STIX]{x1D6E4}$
be a finitely generated abelian group over
![]() $S$
. By definition, this means locally on
$S$
. By definition, this means locally on
![]() $S$
,
$S$
,
![]() $\unicode[STIX]{x1D6E4}$
is isomorphic to the constant sheaf
$\unicode[STIX]{x1D6E4}$
is isomorphic to the constant sheaf
![]() $M_{S}$
, where
$M_{S}$
, where
![]() $M$
is a finitely generate abelian group (in the naive sense). Recall that the Cartier dual of
$M$
is a finitely generate abelian group (in the naive sense). Recall that the Cartier dual of
![]() $\unicode[STIX]{x1D6E4}$
, denoted by
$\unicode[STIX]{x1D6E4}$
, denoted by
![]() $\operatorname{D}(\unicode[STIX]{x1D6E4})$
is the sheaf which assigns every scheme
$\operatorname{D}(\unicode[STIX]{x1D6E4})$
is the sheaf which assigns every scheme
![]() $U$
over
$U$
over
![]() $S$
the group
$S$
the group
 $\operatorname{Hom}(\unicode[STIX]{x1D6E4}\times _{S}U,\mathbb{G}_{m})$
, which is represented by an affine group scheme over
$\operatorname{Hom}(\unicode[STIX]{x1D6E4}\times _{S}U,\mathbb{G}_{m})$
, which is represented by an affine group scheme over
![]() $S$
. We claim that
$S$
. We claim that
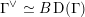 $\unicode[STIX]{x1D6E4}^{\vee }\simeq B\operatorname{D}(\unicode[STIX]{x1D6E4})$
. By (A.1.1), it is enough to show that
$\unicode[STIX]{x1D6E4}^{\vee }\simeq B\operatorname{D}(\unicode[STIX]{x1D6E4})$
. By (A.1.1), it is enough to show that
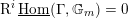 $\operatorname{R}^{i}\text{}\underline{\text{Hom}}(\unicode[STIX]{x1D6E4},\mathbb{G}_{m})=0$
if
$\operatorname{R}^{i}\text{}\underline{\text{Hom}}(\unicode[STIX]{x1D6E4},\mathbb{G}_{m})=0$
if
![]() $i>0$
. This is clear since locally on
$i>0$
. This is clear since locally on
![]() $S$
,
$S$
,
![]() $\unicode[STIX]{x1D6E4}$
is represented by a 2-term complex
$\unicode[STIX]{x1D6E4}$
is represented by a 2-term complex
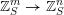 $\mathbb{Z}_{S}^{m}\rightarrow \mathbb{Z}_{S}^{n}$
.
$\mathbb{Z}_{S}^{m}\rightarrow \mathbb{Z}_{S}^{n}$
.
Example A.3.4. Let
![]() $G$
be a group of multiplicative type over
$G$
be a group of multiplicative type over
![]() $S$
, i.e.,
$S$
, i.e.,
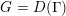 $G=D(\unicode[STIX]{x1D6E4})$
for some finitely generated abelian group
$G=D(\unicode[STIX]{x1D6E4})$
for some finitely generated abelian group
![]() $\unicode[STIX]{x1D6E4}$
over
$\unicode[STIX]{x1D6E4}$
over
![]() $S$
. Let
$S$
. Let
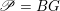 $\mathscr{P}=BG$
, the classifying stack of
$\mathscr{P}=BG$
, the classifying stack of
![]() $G$
. We have
$G$
. We have
 $$\begin{eqnarray}\mathscr{P}^{\vee }\simeq \unicode[STIX]{x1D70F}_{{\leqslant}0}\operatorname{R}\text{}\underline{\text{Hom}}(BG,B\mathbb{G}_{m})\simeq \text{}\underline{\text{Hom}}(G,\mathbb{G}_{m})\simeq \unicode[STIX]{x1D6E4}.\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{P}^{\vee }\simeq \unicode[STIX]{x1D70F}_{{\leqslant}0}\operatorname{R}\text{}\underline{\text{Hom}}(BG,B\mathbb{G}_{m})\simeq \text{}\underline{\text{Hom}}(G,\mathbb{G}_{m})\simeq \unicode[STIX]{x1D6E4}.\end{eqnarray}$$
Definition A.3.5. Let
![]() $\mathscr{P}$
be a Picard stack. We say that
$\mathscr{P}$
be a Picard stack. We say that
![]() $\mathscr{P}$
is dualizable if the canonical 1-morphism
$\mathscr{P}$
is dualizable if the canonical 1-morphism
 $\mathscr{P}\rightarrow \mathscr{P}^{\vee \vee }$
is an isomorphism.
$\mathscr{P}\rightarrow \mathscr{P}^{\vee \vee }$
is an isomorphism.
By the above examples, abelian schemes, finitely generated abelian groups, and the classifying stacks of groups of multiplicative type are dualizable.
Let
![]() $\mathscr{P}$
be a dualizable Picard stack. There is the Poincare line bundle
$\mathscr{P}$
be a dualizable Picard stack. There is the Poincare line bundle
![]() ${\mathcal{L}}_{\mathscr{P}}$
over
${\mathcal{L}}_{\mathscr{P}}$
over
 $\mathscr{P}\times _{S}\mathscr{P}^{\vee }$
. Let
$\mathscr{P}\times _{S}\mathscr{P}^{\vee }$
. Let
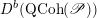 $D^{b}(\operatorname{QCoh}(\mathscr{P}))$
denote the bounded derived category of quasi coherent sheaves on
$D^{b}(\operatorname{QCoh}(\mathscr{P}))$
denote the bounded derived category of quasi coherent sheaves on
![]() $\mathscr{P}$
. We define the Fourier–Mukai functor
$\mathscr{P}$
. We define the Fourier–Mukai functor
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{\mathscr{P}}:D^{b}(\operatorname{QCoh}(\mathscr{P}))\rightarrow D^{b}(\operatorname{QCoh}(\mathscr{P}^{\vee })),\quad \unicode[STIX]{x1D6F7}_{\mathscr{ P}}(F)=(\operatorname{R}p_{2})_{\ast }(\operatorname{L}p_{1}^{\ast }F\otimes ^{}{\mathcal{L}}_{\mathscr{ P}}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{\mathscr{P}}:D^{b}(\operatorname{QCoh}(\mathscr{P}))\rightarrow D^{b}(\operatorname{QCoh}(\mathscr{P}^{\vee })),\quad \unicode[STIX]{x1D6F7}_{\mathscr{ P}}(F)=(\operatorname{R}p_{2})_{\ast }(\operatorname{L}p_{1}^{\ast }F\otimes ^{}{\mathcal{L}}_{\mathscr{ P}}).\end{eqnarray}$$
Here
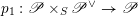 $p_{1}:\mathscr{P}\times _{S}\mathscr{P}^{\vee }\rightarrow \mathscr{P}$
and
$p_{1}:\mathscr{P}\times _{S}\mathscr{P}^{\vee }\rightarrow \mathscr{P}$
and
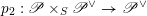 $p_{2}:\mathscr{P}\times _{S}\mathscr{P}^{\vee }\rightarrow \mathscr{P}^{\vee }$
denote the natural projections. It is easy to see in the case when
$p_{2}:\mathscr{P}\times _{S}\mathscr{P}^{\vee }\rightarrow \mathscr{P}^{\vee }$
denote the natural projections. It is easy to see in the case when
![]() $\mathscr{P}$
is of the form given in the above examples,
$\mathscr{P}$
is of the form given in the above examples,
![]() $\unicode[STIX]{x1D6F7}_{\mathscr{P}}$
is an equivalence of categories. Indeed, the case when
$\unicode[STIX]{x1D6F7}_{\mathscr{P}}$
is an equivalence of categories. Indeed, the case when
![]() $\mathscr{P}=A$
follows from the results of Mukai; the case when
$\mathscr{P}=A$
follows from the results of Mukai; the case when
![]() $\mathscr{P}=\unicode[STIX]{x1D6E4}$
or
$\mathscr{P}=\unicode[STIX]{x1D6E4}$
or
![]() $BG$
is clear.
$BG$
is clear.
It is not clear to us whether
![]() $\unicode[STIX]{x1D6F7}_{\mathscr{P}}$
is an equivalence for all dualizable Picard stacks. In the following subsection, we select out a particular class of Picard stacks, called the Beilinson
$\unicode[STIX]{x1D6F7}_{\mathscr{P}}$
is an equivalence for all dualizable Picard stacks. In the following subsection, we select out a particular class of Picard stacks, called the Beilinson
![]() $1$
-motive (following [Reference Donagi and PantevDP12] and Arinkin’s appendix to [Reference Donagi and PantevDP08]), for which the Fourier–Mukai transforms are equivalences.
$1$
-motive (following [Reference Donagi and PantevDP12] and Arinkin’s appendix to [Reference Donagi and PantevDP08]), for which the Fourier–Mukai transforms are equivalences.
A.4 Beilinson 1-motives
Let
![]() $\mathscr{P}_{1},\mathscr{P}_{2}$
be two Picard stacks. We say that
$\mathscr{P}_{1},\mathscr{P}_{2}$
be two Picard stacks. We say that
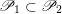 $\mathscr{P}_{1}\subset \mathscr{P}_{2}$
if there is a 1-morphism
$\mathscr{P}_{1}\subset \mathscr{P}_{2}$
if there is a 1-morphism
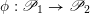 $\unicode[STIX]{x1D719}:\mathscr{P}_{1}\rightarrow \mathscr{P}_{2}$
, which is a faithful embedding.
$\unicode[STIX]{x1D719}:\mathscr{P}_{1}\rightarrow \mathscr{P}_{2}$
, which is a faithful embedding.
Definition A.4.1. We called a Picard stack
![]() $\mathscr{P}$
a Beilinson
$\mathscr{P}$
a Beilinson
![]() $1$
-motive if it admits a two step filtration
$1$
-motive if it admits a two step filtration
![]() $W_{\bullet }\mathscr{P}$
:
$W_{\bullet }\mathscr{P}$
:
 $$\begin{eqnarray}W_{-1}=0\subset W_{0}\subset W_{1}\subset W_{2}=\mathscr{P}\end{eqnarray}$$
$$\begin{eqnarray}W_{-1}=0\subset W_{0}\subset W_{1}\subset W_{2}=\mathscr{P}\end{eqnarray}$$
such that: (i)
 $\operatorname{Gr}_{0}^{W}\simeq BG$
is the classifying stack of a group
$\operatorname{Gr}_{0}^{W}\simeq BG$
is the classifying stack of a group
![]() $G$
of multiplicative type; (ii)
$G$
of multiplicative type; (ii)
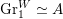 $\operatorname{Gr}_{1}^{W}\simeq A$
is an abelian scheme; and (iii)
$\operatorname{Gr}_{1}^{W}\simeq A$
is an abelian scheme; and (iii)
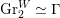 $\operatorname{Gr}_{2}^{W}\simeq \unicode[STIX]{x1D6E4}$
is a finitely generated abelian group.
$\operatorname{Gr}_{2}^{W}\simeq \unicode[STIX]{x1D6E4}$
is a finitely generated abelian group.
Lemma A.4.2. The dual of a Beilinson
![]() $1$
-motive is a Beilinson
$1$
-motive is a Beilinson
![]() $1$
-motive and Beilinson
$1$
-motive and Beilinson
![]() $1$
-motives are dualizable.
$1$
-motives are dualizable.
Proof. This is proved via the induction on the length of the filtration. We use the following fact. Let
 $$\begin{eqnarray}0\rightarrow \mathscr{P}^{\prime }\rightarrow \mathscr{P}\rightarrow \mathscr{P}^{\prime \prime }\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \mathscr{P}^{\prime }\rightarrow \mathscr{P}\rightarrow \mathscr{P}^{\prime \prime }\rightarrow 0\end{eqnarray}$$
be a short exact sequence of Picard stacks. Then
 $$\begin{eqnarray}0\rightarrow (\mathscr{P}^{\prime \prime })^{\vee }\rightarrow \mathscr{P}^{\vee }\rightarrow (\mathscr{P}^{\prime })^{\vee }\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow (\mathscr{P}^{\prime \prime })^{\vee }\rightarrow \mathscr{P}^{\vee }\rightarrow (\mathscr{P}^{\prime })^{\vee }\end{eqnarray}$$
with the right arrow surjective if
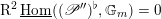 $\operatorname{R}^{2}\text{}\underline{\text{Hom}}((\mathscr{P}^{\prime \prime })^{\flat },\mathbb{G}_{m})=0$
.
$\operatorname{R}^{2}\text{}\underline{\text{Hom}}((\mathscr{P}^{\prime \prime })^{\flat },\mathbb{G}_{m})=0$
.
If
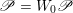 $\mathscr{P}=W_{0}\mathscr{P}$
, this is given by Example A.3.4. If
$\mathscr{P}=W_{0}\mathscr{P}$
, this is given by Example A.3.4. If
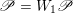 $\mathscr{P}=W_{1}\mathscr{P}$
, we have the following exact sequence
$\mathscr{P}=W_{1}\mathscr{P}$
, we have the following exact sequence
 $$\begin{eqnarray}0\rightarrow BG\rightarrow \mathscr{P}\rightarrow A\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow BG\rightarrow \mathscr{P}\rightarrow A\rightarrow 0.\end{eqnarray}$$
Using the fact that
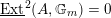 $\text{}\underline{\text{Ext}}^{2}(A,\mathbb{G}_{m})=0$
(see [Reference BreenBre75, Remark 6]), we know that
$\text{}\underline{\text{Ext}}^{2}(A,\mathbb{G}_{m})=0$
(see [Reference BreenBre75, Remark 6]), we know that
![]() $\mathscr{P}$
is also a Beilinson
$\mathscr{P}$
is also a Beilinson
![]() $1$
-motive. In general, we have
$1$
-motive. In general, we have
 $$\begin{eqnarray}0\rightarrow W_{1}\mathscr{P}\rightarrow \mathscr{P}\rightarrow \unicode[STIX]{x1D6E4}\rightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow W_{1}\mathscr{P}\rightarrow \mathscr{P}\rightarrow \unicode[STIX]{x1D6E4}\rightarrow 0,\end{eqnarray}$$
and the lemma follows from the fact
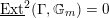 $\text{}\underline{\text{Ext}}^{2}(\unicode[STIX]{x1D6E4},\mathbb{G}_{m})=0$
(see Example A.3.3).◻
$\text{}\underline{\text{Ext}}^{2}(\unicode[STIX]{x1D6E4},\mathbb{G}_{m})=0$
(see Example A.3.3).◻
Corollary A.4.3. Let
![]() $\mathscr{P}$
be a Beilinson
$\mathscr{P}$
be a Beilinson
![]() $1$
-motive, and
$1$
-motive, and
![]() $\mathscr{P}^{\vee }$
be its dual. Then
$\mathscr{P}^{\vee }$
be its dual. Then
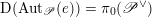 $\operatorname{D}(\operatorname{Aut}_{\mathscr{P}}(e))=\unicode[STIX]{x1D70B}_{0}(\mathscr{P}^{\vee })$
, where
$\operatorname{D}(\operatorname{Aut}_{\mathscr{P}}(e))=\unicode[STIX]{x1D70B}_{0}(\mathscr{P}^{\vee })$
, where
![]() $e$
denotes the unit of
$e$
denotes the unit of
![]() $\mathscr{P}$
and
$\mathscr{P}$
and
![]() $\unicode[STIX]{x1D70B}_{0}$
denotes the group of connected components of
$\unicode[STIX]{x1D70B}_{0}$
denotes the group of connected components of
![]() $\mathscr{P}^{\vee }$
.
$\mathscr{P}^{\vee }$
.
Lemma A.4.4. Let
![]() $\mathscr{P}$
be a Beilinson
$\mathscr{P}$
be a Beilinson
![]() $1$
-motive. Then, locally on
$1$
-motive. Then, locally on
![]() $S$
,
$S$
,
 $$\begin{eqnarray}\mathscr{P}\simeq A\times BG\times \unicode[STIX]{x1D6E4}.\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{P}\simeq A\times BG\times \unicode[STIX]{x1D6E4}.\end{eqnarray}$$
Proof. It is enough to prove that
 $$\begin{eqnarray}\text{}\underline{\text{Ext}}^{1}(\unicode[STIX]{x1D6E4},BG)=\text{}\underline{\text{Ext}}^{1}(\unicode[STIX]{x1D6E4},A)=\text{}\underline{\text{Ext}}^{1}(A,BG)=0.\end{eqnarray}$$
$$\begin{eqnarray}\text{}\underline{\text{Ext}}^{1}(\unicode[STIX]{x1D6E4},BG)=\text{}\underline{\text{Ext}}^{1}(\unicode[STIX]{x1D6E4},A)=\text{}\underline{\text{Ext}}^{1}(A,BG)=0.\end{eqnarray}$$
Clearly,
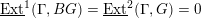 $\text{}\underline{\text{Ext}}^{1}(\unicode[STIX]{x1D6E4},BG)=\text{}\underline{\text{Ext}}^{2}(\unicode[STIX]{x1D6E4},G)=0$
. To see that
$\text{}\underline{\text{Ext}}^{1}(\unicode[STIX]{x1D6E4},BG)=\text{}\underline{\text{Ext}}^{2}(\unicode[STIX]{x1D6E4},G)=0$
. To see that
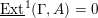 $\text{}\underline{\text{Ext}}^{1}(\unicode[STIX]{x1D6E4},A)=0$
, we can assume that
$\text{}\underline{\text{Ext}}^{1}(\unicode[STIX]{x1D6E4},A)=0$
, we can assume that
 $\unicode[STIX]{x1D6E4}=\mathbb{Z}/n\mathbb{Z}$
. Then it follows that
$\unicode[STIX]{x1D6E4}=\mathbb{Z}/n\mathbb{Z}$
. Then it follows that
![]() $A\stackrel{n}{\rightarrow }A$
is surjective in the flat topology that
$A\stackrel{n}{\rightarrow }A$
is surjective in the flat topology that
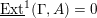 $\text{}\underline{\text{Ext}}^{1}(\unicode[STIX]{x1D6E4},A)=0$
.
$\text{}\underline{\text{Ext}}^{1}(\unicode[STIX]{x1D6E4},A)=0$
.
To see that
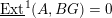 $\text{}\underline{\text{Ext}}^{1}(A,BG)=0$
, let
$\text{}\underline{\text{Ext}}^{1}(A,BG)=0$
, let
![]() $\mathscr{P}$
to the Beilinson
$\mathscr{P}$
to the Beilinson
![]() $1$
-motive corresponding to a class in
$1$
-motive corresponding to a class in
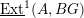 $\text{}\underline{\text{Ext}}^{1}(A,BG)$
. Taking the dual, we have
$\text{}\underline{\text{Ext}}^{1}(A,BG)$
. Taking the dual, we have
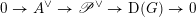 $0\rightarrow A^{\vee }\rightarrow \mathscr{P}^{\vee }\rightarrow \operatorname{D}(G)\rightarrow 0$
. Therefore, locally on
$0\rightarrow A^{\vee }\rightarrow \mathscr{P}^{\vee }\rightarrow \operatorname{D}(G)\rightarrow 0$
. Therefore, locally on
![]() $S$
,
$S$
,
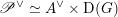 $\mathscr{P}^{\vee }\simeq A^{\vee }\times \operatorname{D}(G)$
, and therefore, locally on
$\mathscr{P}^{\vee }\simeq A^{\vee }\times \operatorname{D}(G)$
, and therefore, locally on
![]() $S$
,
$S$
,
 $\mathscr{P}^{\vee \vee }\simeq A\times BG$
.◻
$\mathscr{P}^{\vee \vee }\simeq A\times BG$
.◻
Definition A.4.5 (Cf. [Reference ArinkinAri08]).
We say that a Picard stack
![]() $\mathscr{P}$
is good if it satisfies the following two conditions.
$\mathscr{P}$
is good if it satisfies the following two conditions.
-
(1) The Picard stack
 $\mathscr{P}$
is dualizable, i.e., the map
$\mathscr{P}$
is dualizable, i.e., the map
 $r:\mathscr{P}\rightarrow \mathscr{P}^{\vee \vee }$
is an isomorphism of Picard stacks.
$r:\mathscr{P}\rightarrow \mathscr{P}^{\vee \vee }$
is an isomorphism of Picard stacks. -
(2) The functor
 $\unicode[STIX]{x1D6F7}_{\mathscr{P}}:D^{b}(\operatorname{QCoh}(\mathscr{P}))\rightarrow D^{b}(\operatorname{QCoh}(\mathscr{P}^{\vee }))$
is an equivalence of categories.
$\unicode[STIX]{x1D6F7}_{\mathscr{P}}:D^{b}(\operatorname{QCoh}(\mathscr{P}))\rightarrow D^{b}(\operatorname{QCoh}(\mathscr{P}^{\vee }))$
is an equivalence of categories.
As explained in §A.3 (see also [Reference Bezrukavnikov and BravermanBB07]), examples of good Picard stacks include
![]() $BG$
,
$BG$
,
![]() $\unicode[STIX]{x1D6E4}$
and abelian schemes over
$\unicode[STIX]{x1D6E4}$
and abelian schemes over
![]() $S$
, as well as fiber products over
$S$
, as well as fiber products over
![]() $S$
of such. More generally, we have the following theorem.
$S$
of such. More generally, we have the following theorem.
Theorem A.4.6 [Reference ArinkinAri08, Proposition A.6].
Let
![]() $\mathscr{P}$
be a Beilinson
$\mathscr{P}$
be a Beilinson
![]() $1$
-motive. Then
$1$
-motive. Then
![]() $\mathscr{P}$
is ‘good’ in the sense of Definition A.4.5. In particular, the functor
$\mathscr{P}$
is ‘good’ in the sense of Definition A.4.5. In particular, the functor
![]() $\unicode[STIX]{x1D6F7}_{\mathscr{P}}$
is an equivalence of categories.
$\unicode[STIX]{x1D6F7}_{\mathscr{P}}$
is an equivalence of categories.
Proof. Indeed, the property of being good is fpqc-local on
![]() $S$
. This can be seen by lifting
$S$
. This can be seen by lifting
![]() $\unicode[STIX]{x1D6F7}_{\mathscr{P}}$
to a functor between stable
$\unicode[STIX]{x1D6F7}_{\mathscr{P}}$
to a functor between stable
![]() $\infty$
-categories of quasi-coherent sheaves and then applying a descent argument. Therefore, the theorem follows from Lemma A.4.4 and the above examples.
$\infty$
-categories of quasi-coherent sheaves and then applying a descent argument. Therefore, the theorem follows from Lemma A.4.4 and the above examples.
Alternatively, similarly to the usual Fourier–Mukai transform, one can show directly that in our generality there is still an isomorphism of functors
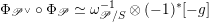 $\unicode[STIX]{x1D6F7}_{\mathscr{P}^{\vee }}\circ \unicode[STIX]{x1D6F7}_{\mathscr{P}}\simeq \unicode[STIX]{x1D714}_{\mathscr{P}/S}^{-1}\otimes (-1)^{\ast }[-g]$
, where
$\unicode[STIX]{x1D6F7}_{\mathscr{P}^{\vee }}\circ \unicode[STIX]{x1D6F7}_{\mathscr{P}}\simeq \unicode[STIX]{x1D714}_{\mathscr{P}/S}^{-1}\otimes (-1)^{\ast }[-g]$
, where
![]() $\unicode[STIX]{x1D714}_{\mathscr{P}/S}$
is the canonical sheaf and
$\unicode[STIX]{x1D714}_{\mathscr{P}/S}$
is the canonical sheaf and
![]() $g$
is the relative dimension of
$g$
is the relative dimension of
![]() $\mathscr{P}/S$
.Footnote
12
By the argument as in [Reference MukaiMuk85] (see also [Reference LaumonLau96]), one reduces to show that the kernel complex
$\mathscr{P}/S$
.Footnote
12
By the argument as in [Reference MukaiMuk85] (see also [Reference LaumonLau96]), one reduces to show that the kernel complex
 $$\begin{eqnarray}\operatorname{R}p_{12\ast }(\operatorname{L}p_{13}^{\ast }{\mathcal{L}}_{\mathscr{P}}\otimes ^{}\operatorname{L}p_{23}^{\ast }{\mathcal{L}}_{\mathscr{P}})\simeq m^{\ast }\operatorname{R}p_{1\ast }{\mathcal{L}}_{\mathscr{P}}\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{R}p_{12\ast }(\operatorname{L}p_{13}^{\ast }{\mathcal{L}}_{\mathscr{P}}\otimes ^{}\operatorname{L}p_{23}^{\ast }{\mathcal{L}}_{\mathscr{P}})\simeq m^{\ast }\operatorname{R}p_{1\ast }{\mathcal{L}}_{\mathscr{P}}\end{eqnarray}$$
for the functor
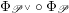 $\unicode[STIX]{x1D6F7}_{\mathscr{P}^{\vee }}\circ \unicode[STIX]{x1D6F7}_{\mathscr{P}}$
is isomorphic to the kernel complex
$\unicode[STIX]{x1D6F7}_{\mathscr{P}^{\vee }}\circ \unicode[STIX]{x1D6F7}_{\mathscr{P}}$
is isomorphic to the kernel complex
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}_{\ast }(\unicode[STIX]{x1D714}_{\mathscr{P}/S}^{-1})[-g]\simeq m^{\ast }e_{\ast }(e^{\ast }\unicode[STIX]{x1D714}_{\mathscr{P}/S}^{-1})[-g]\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{\ast }(\unicode[STIX]{x1D714}_{\mathscr{P}/S}^{-1})[-g]\simeq m^{\ast }e_{\ast }(e^{\ast }\unicode[STIX]{x1D714}_{\mathscr{P}/S}^{-1})[-g]\end{eqnarray}$$
for
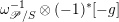 $\unicode[STIX]{x1D714}_{\mathscr{P}/S}^{-1}\otimes (-1)^{\ast }[-g]$
. Here
$\unicode[STIX]{x1D714}_{\mathscr{P}/S}^{-1}\otimes (-1)^{\ast }[-g]$
. Here
![]() $p_{ij}$
are the projections of
$p_{ij}$
are the projections of
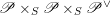 $\mathscr{P}\times _{S}\mathscr{P}\times _{S}\mathscr{P}^{\vee }$
on the
$\mathscr{P}\times _{S}\mathscr{P}\times _{S}\mathscr{P}^{\vee }$
on the
![]() $(i,j)$
-factors,
$(i,j)$
-factors,
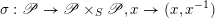 $\unicode[STIX]{x1D70E}:\mathscr{P}\rightarrow \mathscr{P}\times _{S}\mathscr{P},x\rightarrow (x,x^{-1})$
and
$\unicode[STIX]{x1D70E}:\mathscr{P}\rightarrow \mathscr{P}\times _{S}\mathscr{P},x\rightarrow (x,x^{-1})$
and
 $e:S\rightarrow \mathscr{P}$
is the unit morphism.
$e:S\rightarrow \mathscr{P}$
is the unit morphism.
To prove this, we first observe that there is a natural map
 $$\begin{eqnarray}\operatorname{R}p_{1\ast }{\mathcal{L}}_{\mathscr{P}}\simeq \operatorname{R}^{g}p_{1\ast }{\mathcal{L}}_{\mathscr{P}}[-g]\rightarrow e_{\ast }\operatorname{R}^{g}pr_{S\ast }{\mathcal{O}}_{\mathscr{P}^{\vee }}[-g]\rightarrow e_{\ast }(e^{\ast }\unicode[STIX]{x1D714}_{\mathscr{P}/S}^{-1})[-g].\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{R}p_{1\ast }{\mathcal{L}}_{\mathscr{P}}\simeq \operatorname{R}^{g}p_{1\ast }{\mathcal{L}}_{\mathscr{P}}[-g]\rightarrow e_{\ast }\operatorname{R}^{g}pr_{S\ast }{\mathcal{O}}_{\mathscr{P}^{\vee }}[-g]\rightarrow e_{\ast }(e^{\ast }\unicode[STIX]{x1D714}_{\mathscr{P}/S}^{-1})[-g].\end{eqnarray}$$
We claim that the map above is an isomorphism, and hence induces
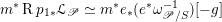 $m^{\ast }\operatorname{R}p_{1\ast }{\mathcal{L}}_{\mathscr{P}}\simeq m^{\ast }e_{\ast }(e^{\ast }\unicode[STIX]{x1D714}_{\mathscr{P}/S}^{-1})[-g]$
. To prove the claim, we observe that, using Lemma A.4.4 and fpqc base change, we can assume
$m^{\ast }\operatorname{R}p_{1\ast }{\mathcal{L}}_{\mathscr{P}}\simeq m^{\ast }e_{\ast }(e^{\ast }\unicode[STIX]{x1D714}_{\mathscr{P}/S}^{-1})[-g]$
. To prove the claim, we observe that, using Lemma A.4.4 and fpqc base change, we can assume
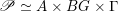 $\mathscr{P}\simeq A\times BG\times \unicode[STIX]{x1D6E4}$
and the claim follows from the results in [Reference MukaiMuk85, p. 519] or [Reference LaumonLau96, Lemma 1.2.5].◻
$\mathscr{P}\simeq A\times BG\times \unicode[STIX]{x1D6E4}$
and the claim follows from the results in [Reference MukaiMuk85, p. 519] or [Reference LaumonLau96, Lemma 1.2.5].◻
Entirely similar arguments as in [Reference MukaiMuk81, p. 160] and [Reference LaumonLau96, Corollary 1.3.3] give us the following.
Theorem A.4.7. Let
![]() $\mathscr{P}$
be a Beilinson
$\mathscr{P}$
be a Beilinson
![]() $1$
-motive. Let
$1$
-motive. Let
 $$\begin{eqnarray}\ast :D^{b}(\operatorname{QCoh}(\mathscr{P}))\times D^{b}(\operatorname{QCoh}(\mathscr{P}))\rightarrow D^{b}(\operatorname{QCoh}(\mathscr{P}))\end{eqnarray}$$
$$\begin{eqnarray}\ast :D^{b}(\operatorname{QCoh}(\mathscr{P}))\times D^{b}(\operatorname{QCoh}(\mathscr{P}))\rightarrow D^{b}(\operatorname{QCoh}(\mathscr{P}))\end{eqnarray}$$
be the functor defined by
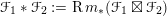 ${\mathcal{F}}_{1}\ast {\mathcal{F}}_{2}:=\operatorname{R}m_{\ast }({\mathcal{F}}_{1}\boxtimes {\mathcal{F}}_{2})$
. We called
${\mathcal{F}}_{1}\ast {\mathcal{F}}_{2}:=\operatorname{R}m_{\ast }({\mathcal{F}}_{1}\boxtimes {\mathcal{F}}_{2})$
. We called
![]() $\ast$
the convolution product. Then there are canonical isomorphisms
$\ast$
the convolution product. Then there are canonical isomorphisms
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{\mathscr{P}}({\mathcal{F}}_{1}\ast {\mathcal{F}}_{2})\simeq \unicode[STIX]{x1D6F7}_{\mathscr{P}}({\mathcal{F}}_{1})\otimes ^{}\unicode[STIX]{x1D6F7}_{\mathscr{P}}({\mathcal{F}}_{2})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{\mathscr{P}}({\mathcal{F}}_{1}\ast {\mathcal{F}}_{2})\simeq \unicode[STIX]{x1D6F7}_{\mathscr{P}}({\mathcal{F}}_{1})\otimes ^{}\unicode[STIX]{x1D6F7}_{\mathscr{P}}({\mathcal{F}}_{2})\end{eqnarray}$$
and
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{\mathscr{P}}({\mathcal{F}}_{1}\otimes ^{}{\mathcal{F}}_{2})\simeq (\unicode[STIX]{x1D6F7}_{\mathscr{P}}({\mathcal{F}}_{1})\ast \unicode[STIX]{x1D6F7}_{\mathscr{P}}({\mathcal{F}}_{2}))\otimes ^{}\unicode[STIX]{x1D714}_{\mathscr{P}^{\vee }/S}[g].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{\mathscr{P}}({\mathcal{F}}_{1}\otimes ^{}{\mathcal{F}}_{2})\simeq (\unicode[STIX]{x1D6F7}_{\mathscr{P}}({\mathcal{F}}_{1})\ast \unicode[STIX]{x1D6F7}_{\mathscr{P}}({\mathcal{F}}_{2}))\otimes ^{}\unicode[STIX]{x1D714}_{\mathscr{P}^{\vee }/S}[g].\end{eqnarray}$$
A.5 Multiplicative torsors and extensions of Beilinson 1-motives
Let us return to the general set-up. Let
![]() ${\mathcal{T}}$
be a fixed site and let
${\mathcal{T}}$
be a fixed site and let
![]() $\mathscr{P}$
be a Picard stack over
$\mathscr{P}$
be a Picard stack over
![]() ${\mathcal{T}}$
. A torsor of
${\mathcal{T}}$
. A torsor of
![]() $\mathscr{P}$
is a stack
$\mathscr{P}$
is a stack
![]() $\mathscr{Q}$
over
$\mathscr{Q}$
over
![]() ${\mathcal{T}}$
, together with a bi-functor
${\mathcal{T}}$
, together with a bi-functor
 $$\begin{eqnarray}\operatorname{Action}:\mathscr{P}\times \mathscr{Q}\rightarrow \mathscr{Q},\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Action}:\mathscr{P}\times \mathscr{Q}\rightarrow \mathscr{Q},\end{eqnarray}$$
satisfying the following properties.
-
(i) The bi-functor
 $\operatorname{Action}$
defines a monoidal action of
$\operatorname{Action}$
defines a monoidal action of
 $\mathscr{P}$
on
$\mathscr{P}$
on
 $\mathscr{Q}$
.
$\mathscr{Q}$
. -
(ii) For every
 $V\in {\mathcal{T}}$
, there exists a covering
$V\in {\mathcal{T}}$
, there exists a covering
 $U\rightarrow V$
, such that
$U\rightarrow V$
, such that
 $\mathscr{Q}(U)$
is non-empty.
$\mathscr{Q}(U)$
is non-empty. -
(iii) For every
 $U\in {\mathcal{T}}$
such that
$U\in {\mathcal{T}}$
such that
 $\mathscr{Q}(U)$
is non-empty and let
$\mathscr{Q}(U)$
is non-empty and let
 $D\in \mathscr{Q}(U)$
, the functor is an equivalence.
$D\in \mathscr{Q}(U)$
, the functor is an equivalence. $$\begin{eqnarray}\mathscr{P}(U)\rightarrow \mathscr{Q}(U),\quad C\mapsto \operatorname{Action}(C,D)\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{P}(U)\rightarrow \mathscr{Q}(U),\quad C\mapsto \operatorname{Action}(C,D)\end{eqnarray}$$
In the case when
![]() $\mathscr{P}$
is the Picard stack of
$\mathscr{P}$
is the Picard stack of
![]() $G$
-torsors for some sheaf of abelian groups
$G$
-torsors for some sheaf of abelian groups
![]() $G$
, people usually call a
$G$
, people usually call a
![]() $\mathscr{P}$
-torsor
$\mathscr{P}$
-torsor
![]() $\mathscr{Q}$
a
$\mathscr{Q}$
a
![]() $G$
-gerbe.
$G$
-gerbe.
All
![]() $\mathscr{P}$
-torsors form a 2-category, denoted by
$\mathscr{P}$
-torsors form a 2-category, denoted by
![]() $B\mathscr{P}$
, which is canonically enriched over itself [Reference Osipov and ZhuOZ11, §2.3]. That is, given two
$B\mathscr{P}$
, which is canonically enriched over itself [Reference Osipov and ZhuOZ11, §2.3]. That is, given two
![]() $\mathscr{P}$
-torsors
$\mathscr{P}$
-torsors
![]() $\mathscr{Q}_{1},\mathscr{Q}_{2}$
,
$\mathscr{Q}_{1},\mathscr{Q}_{2}$
,
 $\text{}\underline{\operatorname{Hom}}_{\mathscr{P}}(\mathscr{Q}_{1},\mathscr{Q}_{2})$
is a natural
$\text{}\underline{\operatorname{Hom}}_{\mathscr{P}}(\mathscr{Q}_{1},\mathscr{Q}_{2})$
is a natural
![]() $\mathscr{P}$
-torsor. An object in
$\mathscr{P}$
-torsor. An object in
 $\text{}\underline{\operatorname{Hom}}_{\mathscr{P}}(\mathscr{Q}_{1},\mathscr{Q}_{2})$
induces an equivalence between
$\text{}\underline{\operatorname{Hom}}_{\mathscr{P}}(\mathscr{Q}_{1},\mathscr{Q}_{2})$
induces an equivalence between
![]() $\mathscr{Q}_{1}$
and
$\mathscr{Q}_{1}$
and
![]() $\mathscr{Q}_{2}$
. In addition, there is a monoidal structure on
$\mathscr{Q}_{2}$
. In addition, there is a monoidal structure on
![]() $B\mathscr{P}$
making
$B\mathscr{P}$
making
![]() $B\mathscr{P}$
a Picard 2-stack.
$B\mathscr{P}$
a Picard 2-stack.
Remark A.5.1. Let
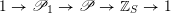 $1\rightarrow \mathscr{P}_{1}\rightarrow \mathscr{P}\rightarrow \mathbb{Z}_{S}\rightarrow 1$
be an exact sequence of Picard stacks. Then
$1\rightarrow \mathscr{P}_{1}\rightarrow \mathscr{P}\rightarrow \mathbb{Z}_{S}\rightarrow 1$
be an exact sequence of Picard stacks. Then
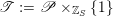 $\mathscr{T}:=\mathscr{P}\times _{\mathbb{Z}_{S}}\{1\}$
is naturally a
$\mathscr{T}:=\mathscr{P}\times _{\mathbb{Z}_{S}}\{1\}$
is naturally a
![]() $\mathscr{P}_{1}$
-torsor. As explained in [Reference ArinkinAri08] and [Reference TravkinTra11, §3.1], the correspondence
$\mathscr{P}_{1}$
-torsor. As explained in [Reference ArinkinAri08] and [Reference TravkinTra11, §3.1], the correspondence
 $\mathscr{P}\rightarrow \mathscr{T}$
induces an equivalence of 2-categories between extensions of
$\mathscr{P}\rightarrow \mathscr{T}$
induces an equivalence of 2-categories between extensions of
![]() $\mathbb{Z}_{S}$
by
$\mathbb{Z}_{S}$
by
![]() $\mathscr{P}_{1}$
and
$\mathscr{P}_{1}$
and
![]() $\mathscr{P}_{1}$
-torsors.
$\mathscr{P}_{1}$
-torsors.
Now, let
![]() $\mathscr{P}$
and
$\mathscr{P}$
and
![]() $\mathscr{P}_{1}$
be two Picard stacks and let
$\mathscr{P}_{1}$
be two Picard stacks and let
![]() $\mathscr{G}$
be a
$\mathscr{G}$
be a
![]() $\mathscr{P}_{1}$
-torsor over
$\mathscr{P}_{1}$
-torsor over
![]() $\mathscr{P}$
. Let
$\mathscr{P}$
. Let
 $m:\mathscr{P}\times \mathscr{P}\rightarrow \mathscr{P}$
,
$m:\mathscr{P}\times \mathscr{P}\rightarrow \mathscr{P}$
,
 $e:{\mathcal{T}}\rightarrow \mathscr{P}$
be the multiplication morphism and the unit morphism respectively, and let
$e:{\mathcal{T}}\rightarrow \mathscr{P}$
be the multiplication morphism and the unit morphism respectively, and let
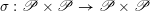 $\unicode[STIX]{x1D70E}:\mathscr{P}\times \mathscr{P}\rightarrow \mathscr{P}\times \mathscr{P}$
be the flip map
$\unicode[STIX]{x1D70E}:\mathscr{P}\times \mathscr{P}\rightarrow \mathscr{P}\times \mathscr{P}$
be the flip map
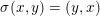 $\unicode[STIX]{x1D70E}(x,y)=(y,x)$
.
$\unicode[STIX]{x1D70E}(x,y)=(y,x)$
.
Definition A.5.2. A commutative group structure on
![]() $\mathscr{G}$
consists of the following data:
$\mathscr{G}$
consists of the following data:
-
(i) an equivalence
 $M:\mathscr{G}\boxtimes \mathscr{G}\simeq m^{\ast }\mathscr{G}$
of
$M:\mathscr{G}\boxtimes \mathscr{G}\simeq m^{\ast }\mathscr{G}$
of
 $\mathscr{P}_{1}$
-torsors over
$\mathscr{P}_{1}$
-torsors over
 $\mathscr{P}\times \mathscr{P}$
;
$\mathscr{P}\times \mathscr{P}$
; -
(ii) a
 $2$
-morphism
$2$
-morphism
 $\unicode[STIX]{x1D6FE}$
between the resulting two
$\unicode[STIX]{x1D6FE}$
between the resulting two
 $1$
-morphisms between
$1$
-morphisms between
 $\mathscr{G}\boxtimes \mathscr{G}\boxtimes \mathscr{G}$
and
$\mathscr{G}\boxtimes \mathscr{G}\boxtimes \mathscr{G}$
and
 $m^{\ast }\mathscr{G}$
over
$m^{\ast }\mathscr{G}$
over
 $\mathscr{P}\times \mathscr{P}\times \mathscr{P}$
, which satisfies the cocycle condition;
$\mathscr{P}\times \mathscr{P}\times \mathscr{P}$
, which satisfies the cocycle condition; -
(iii) a
 $2$
-morphism
$2$
-morphism
 $i:\unicode[STIX]{x1D70E}^{\ast }M\simeq M$
such that
$i:\unicode[STIX]{x1D70E}^{\ast }M\simeq M$
such that
 $i^{2}=\text{id}$
.
$i^{2}=\text{id}$
.
(Note that
![]() $\unicode[STIX]{x1D70E}^{\ast }(M)$
is another
$\unicode[STIX]{x1D70E}^{\ast }(M)$
is another
![]() $1$
-morphism between
$1$
-morphism between
![]() $m^{\ast }\mathscr{G}$
and
$m^{\ast }\mathscr{G}$
and
![]() $\mathscr{G}\boxtimes \mathscr{G}$
.)
$\mathscr{G}\boxtimes \mathscr{G}$
.)
Clearly, all
![]() $\mathscr{P}_{1}$
-torsors over
$\mathscr{P}_{1}$
-torsors over
![]() $\mathscr{P}$
with a commutative group structure also form a
$\mathscr{P}$
with a commutative group structure also form a
![]() $2$
-category.
$2$
-category.
We have the following lemma.
Lemma A.5.3. A commutative group structure on
![]() $\mathscr{G}$
makes
$\mathscr{G}$
makes
![]() $\mathscr{G}$
into a Picard stack which fits into the following short exact sequence:
$\mathscr{G}$
into a Picard stack which fits into the following short exact sequence:
 $$\begin{eqnarray}0\rightarrow \mathscr{P}_{1}\rightarrow \mathscr{G}\rightarrow \mathscr{P}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \mathscr{P}_{1}\rightarrow \mathscr{G}\rightarrow \mathscr{P}\rightarrow 0.\end{eqnarray}$$
In particular, if
![]() $\mathscr{P}$
is a Beilinson
$\mathscr{P}$
is a Beilinson
![]() $1$
-motive, and
$1$
-motive, and
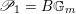 $\mathscr{P}_{1}=B\mathbb{G}_{m}$
, then
$\mathscr{P}_{1}=B\mathbb{G}_{m}$
, then
![]() $\mathscr{G}$
is a Beilinson
$\mathscr{G}$
is a Beilinson
![]() $1$
-motive. In this case, we also call
$1$
-motive. In this case, we also call
![]() $\mathscr{G}$
a multiplicative
$\mathscr{G}$
a multiplicative
![]() $\mathbb{G}_{m}$
-gerbe over
$\mathbb{G}_{m}$
-gerbe over
![]() $\mathscr{P}$
.
$\mathscr{P}$
.
Definition A.5.4. A multiplicative splitting of a
![]() $\mathscr{P}_{1}$
-torsor
$\mathscr{P}_{1}$
-torsor
![]() $\mathscr{G}$
over
$\mathscr{G}$
over
![]() $\mathscr{P}$
with a commutative group structure is a
$\mathscr{P}$
with a commutative group structure is a
![]() $1$
-morphism (in the category of all
$1$
-morphism (in the category of all
![]() $\mathscr{P}_{1}$
-torsors over
$\mathscr{P}_{1}$
-torsors over
![]() $\mathscr{P}$
with a commutative group structure):
$\mathscr{P}$
with a commutative group structure):
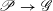 $\mathscr{P}\rightarrow \mathscr{G}$
.
$\mathscr{P}\rightarrow \mathscr{G}$
.
A.6 Induction functor
Let
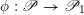 $\unicode[STIX]{x1D719}:\mathscr{P}\rightarrow \mathscr{P}_{1}$
be a morphism of Picard stacks. Then to each
$\unicode[STIX]{x1D719}:\mathscr{P}\rightarrow \mathscr{P}_{1}$
be a morphism of Picard stacks. Then to each
![]() $\mathscr{P}$
-torsor
$\mathscr{P}$
-torsor
![]() $\mathscr{Q}$
we may associate a
$\mathscr{Q}$
we may associate a
![]() $\mathscr{P}_{1}$
-torsor
$\mathscr{P}_{1}$
-torsor
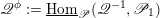 $\mathscr{Q}^{\unicode[STIX]{x1D719}}:=\text{}\underline{\operatorname{Hom}}_{\mathscr{P}}(\mathscr{Q}^{-1},\mathscr{P}_{1})$
whose sections are
$\mathscr{Q}^{\unicode[STIX]{x1D719}}:=\text{}\underline{\operatorname{Hom}}_{\mathscr{P}}(\mathscr{Q}^{-1},\mathscr{P}_{1})$
whose sections are
![]() $\mathscr{P}$
-equivariant functors from
$\mathscr{P}$
-equivariant functors from
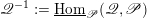 $\mathscr{Q}^{-1}:=\text{}\underline{\operatorname{Hom}}_{\mathscr{P}}(\mathscr{Q},\mathscr{P})$
to
$\mathscr{Q}^{-1}:=\text{}\underline{\operatorname{Hom}}_{\mathscr{P}}(\mathscr{Q},\mathscr{P})$
to
![]() $\mathscr{P}_{1}$
(here
$\mathscr{P}_{1}$
(here
![]() $\mathscr{P}$
acts on
$\mathscr{P}$
acts on
![]() $\mathscr{P}_{1}$
via
$\mathscr{P}_{1}$
via
![]() $\unicode[STIX]{x1D719}$
) and whose morphisms are natural transformations of such functors.
$\unicode[STIX]{x1D719}$
) and whose morphisms are natural transformations of such functors.
We have a canonical functor
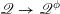 $\mathscr{Q}\rightarrow \mathscr{Q}^{\unicode[STIX]{x1D719}}$
, compatible with their
$\mathscr{Q}\rightarrow \mathscr{Q}^{\unicode[STIX]{x1D719}}$
, compatible with their
![]() $\mathscr{P}$
and
$\mathscr{P}$
and
![]() $\mathscr{P}_{1}$
-structure via
$\mathscr{P}_{1}$
-structure via
![]() $\unicode[STIX]{x1D719}$
. For any section
$\unicode[STIX]{x1D719}$
. For any section
![]() $E$
of
$E$
of
![]() $\mathscr{Q}$
we denote by
$\mathscr{Q}$
we denote by
![]() $E^{\unicode[STIX]{x1D719}}$
the section of
$E^{\unicode[STIX]{x1D719}}$
the section of
![]() $\mathscr{Q}^{\unicode[STIX]{x1D719}}$
induced by the canonical map
$\mathscr{Q}^{\unicode[STIX]{x1D719}}$
induced by the canonical map
 $\mathscr{Q}\rightarrow \mathscr{Q}^{\unicode[STIX]{x1D719}}$
.
$\mathscr{Q}\rightarrow \mathscr{Q}^{\unicode[STIX]{x1D719}}$
.
A.7 Duality for torsors
Let
![]() $\mathscr{Y}$
be an algebraic stack. Let
$\mathscr{Y}$
be an algebraic stack. Let
![]() $\widetilde{\mathscr{Y}}$
be a
$\widetilde{\mathscr{Y}}$
be a
![]() $\mathbb{G}_{m}$
-gerbe over
$\mathbb{G}_{m}$
-gerbe over
![]() $\mathscr{Y}$
, i.e.,
$\mathscr{Y}$
, i.e.,
![]() $\widetilde{\mathscr{Y}}$
is a
$\widetilde{\mathscr{Y}}$
is a
![]() $B\mathbb{G}_{m}$
-torsor over
$B\mathbb{G}_{m}$
-torsor over
![]() $\mathscr{Y}$
. We say
$\mathscr{Y}$
. We say
![]() $\widetilde{\mathscr{Y}}$
is split if it is isomorphic to
$\widetilde{\mathscr{Y}}$
is split if it is isomorphic to
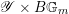 $\mathscr{Y}\times B\mathbb{G}_{m}$
. Let
$\mathscr{Y}\times B\mathbb{G}_{m}$
. Let
 $D^{b}(\operatorname{QCoh}(\widetilde{\mathscr{Y}}))$
be the bounded derived category of quasi coherent sheaves on
$D^{b}(\operatorname{QCoh}(\widetilde{\mathscr{Y}}))$
be the bounded derived category of quasi coherent sheaves on
![]() $\widetilde{\mathscr{Y}}$
. If
$\widetilde{\mathscr{Y}}$
. If
![]() $\widetilde{\mathscr{Y}}$
is split, there is a decomposition
$\widetilde{\mathscr{Y}}$
is split, there is a decomposition
 $$\begin{eqnarray}D^{b}(\operatorname{QCoh}(\widetilde{\mathscr{Y}}))=\bigoplus _{n\in \mathbb{Z}}D^{b}(\operatorname{QCoh}(\widetilde{\mathscr{Y}}))_{n}\end{eqnarray}$$
$$\begin{eqnarray}D^{b}(\operatorname{QCoh}(\widetilde{\mathscr{Y}}))=\bigoplus _{n\in \mathbb{Z}}D^{b}(\operatorname{QCoh}(\widetilde{\mathscr{Y}}))_{n}\end{eqnarray}$$
according to the character of
![]() $\mathbb{G}_{m}$
.Footnote
13
In general we still have such a decomposition given as follows:
$\mathbb{G}_{m}$
.Footnote
13
In general we still have such a decomposition given as follows:
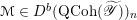 ${\mathcal{M}}\in D^{b}(\operatorname{QCoh}(\widetilde{\mathscr{Y}}))_{n}$
if only if
${\mathcal{M}}\in D^{b}(\operatorname{QCoh}(\widetilde{\mathscr{Y}}))_{n}$
if only if
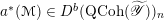 $a^{\ast }({\mathcal{M}})\in D^{b}(\operatorname{QCoh}(\widetilde{\mathscr{Y}}))_{n}$
, where
$a^{\ast }({\mathcal{M}})\in D^{b}(\operatorname{QCoh}(\widetilde{\mathscr{Y}}))_{n}$
, where
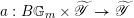 $a:B\mathbb{G}_{m}\times \widetilde{\mathscr{Y}}\rightarrow \widetilde{\mathscr{Y}}$
is the action map.
$a:B\mathbb{G}_{m}\times \widetilde{\mathscr{Y}}\rightarrow \widetilde{\mathscr{Y}}$
is the action map.
Definition A.7.1. The direct summand
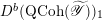 $D^{b}(\operatorname{QCoh}(\widetilde{\mathscr{Y}}))_{1}$
is called the category of twisted sheaves on
$D^{b}(\operatorname{QCoh}(\widetilde{\mathscr{Y}}))_{1}$
is called the category of twisted sheaves on
![]() $\widetilde{\mathscr{Y}}$
.
$\widetilde{\mathscr{Y}}$
.
Now we further assume
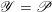 $\mathscr{Y}=\mathscr{P}$
is a Beilinson
$\mathscr{Y}=\mathscr{P}$
is a Beilinson
![]() $1$
-motive over
$1$
-motive over
![]() $S$
and
$S$
and
![]() $\widetilde{\mathscr{Y}}=\mathscr{D}$
is a multiplicative
$\widetilde{\mathscr{Y}}=\mathscr{D}$
is a multiplicative
![]() $\mathbb{G}_{m}$
-gerbe over
$\mathbb{G}_{m}$
-gerbe over
![]() $\mathscr{P}$
. Let
$\mathscr{P}$
. Let
![]() $\mathscr{P}$
and
$\mathscr{P}$
and
![]() $\mathscr{D}$
as above. Then by Lemma A.5.3 we have the following short exact sequence
$\mathscr{D}$
as above. Then by Lemma A.5.3 we have the following short exact sequence
 $$\begin{eqnarray}0\rightarrow B\mathbb{G}_{m}\stackrel{i}{\rightarrow }\mathscr{D}\stackrel{p}{\rightarrow }\mathscr{P}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow B\mathbb{G}_{m}\stackrel{i}{\rightarrow }\mathscr{D}\stackrel{p}{\rightarrow }\mathscr{P}\rightarrow 0\end{eqnarray}$$
as Picard stacks. Note that in this case
![]() $\mathscr{D}$
is also a Beilinson
$\mathscr{D}$
is also a Beilinson
![]() $1$
-motive. Let
$1$
-motive. Let
![]() $\mathscr{D}^{\vee }$
be the dual Beilinson
$\mathscr{D}^{\vee }$
be the dual Beilinson
![]() $1$
-motive. It fits into the short exact sequence
$1$
-motive. It fits into the short exact sequence
 $$\begin{eqnarray}0\rightarrow \mathscr{P}^{\vee }\rightarrow \mathscr{D}^{\vee }\stackrel{\unicode[STIX]{x1D70B}}{\rightarrow }\mathbb{Z}_{S}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \mathscr{P}^{\vee }\rightarrow \mathscr{D}^{\vee }\stackrel{\unicode[STIX]{x1D70B}}{\rightarrow }\mathbb{Z}_{S}\rightarrow 0.\end{eqnarray}$$
Let
 $$\begin{eqnarray}\mathscr{T}_{\mathscr{D}}=\unicode[STIX]{x1D70B}^{-1}(1)\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{T}_{\mathscr{D}}=\unicode[STIX]{x1D70B}^{-1}(1)\end{eqnarray}$$
be the
![]() $\mathscr{P}^{\vee }$
-torsor associated to above extension. We call
$\mathscr{P}^{\vee }$
-torsor associated to above extension. We call
![]() $\mathscr{T}_{\mathscr{D}}$
the stack of multiplicative splitting of
$\mathscr{T}_{\mathscr{D}}$
the stack of multiplicative splitting of
![]() $\mathscr{D}$
. To justify the name, let us give an alternative description of
$\mathscr{D}$
. To justify the name, let us give an alternative description of
![]() $\mathscr{T}_{\mathscr{D}}$
. By definition the dual of
$\mathscr{T}_{\mathscr{D}}$
. By definition the dual of
![]() $\mathscr{D}$
is
$\mathscr{D}$
is
 $$\begin{eqnarray}\mathscr{D}^{\vee }=\text{}\underline{\operatorname{Hom}}(\mathscr{D},B\mathbb{G}_{m}).\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{D}^{\vee }=\text{}\underline{\operatorname{Hom}}(\mathscr{D},B\mathbb{G}_{m}).\end{eqnarray}$$
An element
![]() $s\in \mathscr{D}^{\vee }$
belongs to
$s\in \mathscr{D}^{\vee }$
belongs to
![]() $\mathscr{T}_{\mathscr{D}}$
if and only if the composition
$\mathscr{T}_{\mathscr{D}}$
if and only if the composition
 $$\begin{eqnarray}B\mathbb{G}_{m}\stackrel{i}{\rightarrow }\mathscr{D}\stackrel{s}{\rightarrow }B\mathbb{G}_{m}\end{eqnarray}$$
$$\begin{eqnarray}B\mathbb{G}_{m}\stackrel{i}{\rightarrow }\mathscr{D}\stackrel{s}{\rightarrow }B\mathbb{G}_{m}\end{eqnarray}$$
is equal to the identity. Equivalently,
![]() $s\in \mathscr{T}_{\mathscr{D}}$
gives a splitting of the exact sequence (A.7.2) and according to Definition A.5.4 it is a multiplicative splitting of
$s\in \mathscr{T}_{\mathscr{D}}$
gives a splitting of the exact sequence (A.7.2) and according to Definition A.5.4 it is a multiplicative splitting of
![]() $\mathscr{D}$
.
$\mathscr{D}$
.
The following theorem follows immediately from Theorem A.4.7.
Theorem A.7.2 ([Reference ArinkinAri08], [Reference TravkinTra11, §3.2]).
![]() $(1)$
The Fourier–Mukai functor
$(1)$
The Fourier–Mukai functor
![]() $\unicode[STIX]{x1D6F7}_{\mathscr{D}}$
restricts to an equivalence
$\unicode[STIX]{x1D6F7}_{\mathscr{D}}$
restricts to an equivalence
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{\mathscr{D}}:D^{b}(\operatorname{QCoh}(\mathscr{D}))_{1}\simeq D^{b}(\operatorname{QCoh}(\mathscr{T}_{\mathscr{ D}})).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{\mathscr{D}}:D^{b}(\operatorname{QCoh}(\mathscr{D}))_{1}\simeq D^{b}(\operatorname{QCoh}(\mathscr{T}_{\mathscr{ D}})).\end{eqnarray}$$
![]() $(2)$
There is an action of
$(2)$
There is an action of
 $D^{b}(\operatorname{Qcoh}(\mathscr{P}))$
on
$D^{b}(\operatorname{Qcoh}(\mathscr{P}))$
on
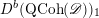 $D^{b}(\operatorname{QCoh}(\mathscr{D}))_{1}$
by tensoring and an action of
$D^{b}(\operatorname{QCoh}(\mathscr{D}))_{1}$
by tensoring and an action of
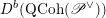 $D^{b}(\operatorname{QCoh}(\mathscr{P}^{\vee }))$
on
$D^{b}(\operatorname{QCoh}(\mathscr{P}^{\vee }))$
on
 $D^{b}(\operatorname{QCoh}(\mathscr{T}_{\mathscr{D}}))$
by convolution. Those two actions are compatible with the above equivalence in the following sense: there is a canonical isomorphism
$D^{b}(\operatorname{QCoh}(\mathscr{T}_{\mathscr{D}}))$
by convolution. Those two actions are compatible with the above equivalence in the following sense: there is a canonical isomorphism
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{\mathscr{D}}({\mathcal{F}}_{1}\otimes ^{}{\mathcal{F}}_{2})\simeq (\unicode[STIX]{x1D6F7}_{\mathscr{D}}({\mathcal{F}}_{1})\ast \unicode[STIX]{x1D6F7}_{\mathscr{D}}({\mathcal{F}}_{2}))\otimes ^{}\unicode[STIX]{x1D714}_{\mathscr{P}^{\vee }/S}[g]\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{\mathscr{D}}({\mathcal{F}}_{1}\otimes ^{}{\mathcal{F}}_{2})\simeq (\unicode[STIX]{x1D6F7}_{\mathscr{D}}({\mathcal{F}}_{1})\ast \unicode[STIX]{x1D6F7}_{\mathscr{D}}({\mathcal{F}}_{2}))\otimes ^{}\unicode[STIX]{x1D714}_{\mathscr{P}^{\vee }/S}[g]\end{eqnarray}$$
for
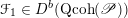 ${\mathcal{F}}_{1}\in D^{b}(\operatorname{Qcoh}(\mathscr{P}))$
and
${\mathcal{F}}_{1}\in D^{b}(\operatorname{Qcoh}(\mathscr{P}))$
and
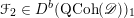 ${\mathcal{F}}_{2}\in D^{b}(\operatorname{QCoh}(\mathscr{D}))_{1}$
. Here
${\mathcal{F}}_{2}\in D^{b}(\operatorname{QCoh}(\mathscr{D}))_{1}$
. Here
![]() $\unicode[STIX]{x1D714}_{\mathscr{P}^{\vee }/S}$
is the canonical sheaf and
$\unicode[STIX]{x1D714}_{\mathscr{P}^{\vee }/S}$
is the canonical sheaf and
![]() $g$
is the relative dimension of
$g$
is the relative dimension of
![]() $\mathscr{P}/S$
.
$\mathscr{P}/S$
.
![]() $(3)$
The convolution product
$(3)$
The convolution product
![]() $\ast$
on
$\ast$
on
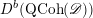 $D^{b}(\operatorname{QCoh}(\mathscr{D}))$
induces a convolution product on
$D^{b}(\operatorname{QCoh}(\mathscr{D}))$
induces a convolution product on
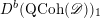 $D^{b}(\operatorname{QCoh}(\mathscr{D}))_{1}$
(by abuse of notation we still denote it by
$D^{b}(\operatorname{QCoh}(\mathscr{D}))_{1}$
(by abuse of notation we still denote it by
![]() $\ast$
). On the other hand, the category
$\ast$
). On the other hand, the category
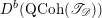 $D^{b}(\operatorname{QCoh}(\mathscr{T}_{\mathscr{D}}))$
has the usual monoidal structure by tensoring. The equivalence
$D^{b}(\operatorname{QCoh}(\mathscr{T}_{\mathscr{D}}))$
has the usual monoidal structure by tensoring. The equivalence
![]() $\unicode[STIX]{x1D6F7}_{\mathscr{D}}$
is compatible with those monoidal structures: there is a canonical isomorphism
$\unicode[STIX]{x1D6F7}_{\mathscr{D}}$
is compatible with those monoidal structures: there is a canonical isomorphism
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{\mathscr{D}}({\mathcal{F}}_{1}\ast {\mathcal{F}}_{2})\simeq \unicode[STIX]{x1D6F7}_{\mathscr{D}}({\mathcal{F}}_{1})\otimes \unicode[STIX]{x1D6F7}_{\mathscr{D}}({\mathcal{F}}_{2})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{\mathscr{D}}({\mathcal{F}}_{1}\ast {\mathcal{F}}_{2})\simeq \unicode[STIX]{x1D6F7}_{\mathscr{D}}({\mathcal{F}}_{1})\otimes \unicode[STIX]{x1D6F7}_{\mathscr{D}}({\mathcal{F}}_{2})\end{eqnarray}$$
for
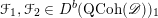 ${\mathcal{F}}_{1},{\mathcal{F}}_{2}\in D^{b}(\operatorname{QCoh}(\mathscr{D}))_{1}$
.
${\mathcal{F}}_{1},{\mathcal{F}}_{2}\in D^{b}(\operatorname{QCoh}(\mathscr{D}))_{1}$
.
Appendix B
 ${\mathcal{D}}$
-modules on stacks and Azumaya property
${\mathcal{D}}$
-modules on stacks and Azumaya property
In this section we review some basic facts about
![]() ${\mathcal{D}}$
-modules on algebraic stacks and the Azumaya property of the sheaf of differential operators. Standard references are [Reference Beilinson and DrinfeldBD91] and [Reference Bezrukavnikov and BravermanBB07].
${\mathcal{D}}$
-modules on algebraic stacks and the Azumaya property of the sheaf of differential operators. Standard references are [Reference Beilinson and DrinfeldBD91] and [Reference Bezrukavnikov and BravermanBB07].
B.1 Azumaya algebras and twisted sheaves
Let us begin with a review of the basic definition of Azumaya algebras and the category of twisted sheaves. Let
![]() $S$
be a Noetherian scheme. Let
$S$
be a Noetherian scheme. Let
![]() $\mathscr{X}$
be an algebraic stack over
$\mathscr{X}$
be an algebraic stack over
![]() $S$
. Recall that an Azumaya algebra
$S$
. Recall that an Azumaya algebra
![]() ${\mathcal{A}}$
over
${\mathcal{A}}$
over
![]() $\mathscr{X}$
is a quasi-coherent sheaf of
$\mathscr{X}$
is a quasi-coherent sheaf of
![]() ${\mathcal{O}}_{\mathscr{X}}$
-algebras, which is locally in smooth topology isomorphic to
${\mathcal{O}}_{\mathscr{X}}$
-algebras, which is locally in smooth topology isomorphic to
![]() ${\mathcal{E}}nd({\mathcal{V}})$
for some vector bundle
${\mathcal{E}}nd({\mathcal{V}})$
for some vector bundle
![]() ${\mathcal{V}}$
on
${\mathcal{V}}$
on
![]() $\mathscr{X}$
. Such an isomorphism between
$\mathscr{X}$
. Such an isomorphism between
![]() ${\mathcal{A}}$
and the matrix algebra is called a splitting of
${\mathcal{A}}$
and the matrix algebra is called a splitting of
![]() ${\mathcal{A}}$
. Given an Azumaya algebra
${\mathcal{A}}$
. Given an Azumaya algebra
![]() ${\mathcal{A}}$
on
${\mathcal{A}}$
on
![]() $\mathscr{X}$
, one can associate to it the
$\mathscr{X}$
, one can associate to it the
![]() $\mathbb{G}_{m}$
-gerbe
$\mathbb{G}_{m}$
-gerbe
![]() $\mathscr{D}_{{\mathcal{A}}}$
of splittings over
$\mathscr{D}_{{\mathcal{A}}}$
of splittings over
![]() $\mathscr{X}$
, i.e., for any
$\mathscr{X}$
, i.e., for any
![]() $U\rightarrow S$
we have
$U\rightarrow S$
we have
 $$\begin{eqnarray}\mathscr{D}_{{\mathcal{A}}}(U)=\{(x,{\mathcal{V}},i)|x\in \mathscr{X}(U),i:{\mathcal{E}}nd({\mathcal{V}})\simeq x^{\ast }({\mathcal{A}})\}.\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{D}_{{\mathcal{A}}}(U)=\{(x,{\mathcal{V}},i)|x\in \mathscr{X}(U),i:{\mathcal{E}}nd({\mathcal{V}})\simeq x^{\ast }({\mathcal{A}})\}.\end{eqnarray}$$
We will use the following proposition in what follows.
Proposition B.1.1 [Reference Donagi and PantevDP08, §2.1.2].
Let
![]() ${\mathcal{A}}$
be a sheaf of Azumaya algebras on
${\mathcal{A}}$
be a sheaf of Azumaya algebras on
![]() $\mathscr{X}$
. There is the following equivalence of categories
$\mathscr{X}$
. There is the following equivalence of categories
 $$\begin{eqnarray}\operatorname{QCoh}(\mathscr{D}_{{\mathcal{A}}})_{1}\simeq {\mathcal{A}}\text{-}\text{mod}(\operatorname{QCoh}(\mathscr{X})),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{QCoh}(\mathscr{D}_{{\mathcal{A}}})_{1}\simeq {\mathcal{A}}\text{-}\text{mod}(\operatorname{QCoh}(\mathscr{X})),\end{eqnarray}$$
where
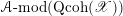 ${\mathcal{A}}\text{-}\text{mod}(\operatorname{Qcoh}(\mathscr{X}))$
is the category of
${\mathcal{A}}\text{-}\text{mod}(\operatorname{Qcoh}(\mathscr{X}))$
is the category of
![]() ${\mathcal{A}}$
-modules which is quasi-coherent as
${\mathcal{A}}$
-modules which is quasi-coherent as
![]() ${\mathcal{O}}_{\mathscr{X}}$
-modules.
${\mathcal{O}}_{\mathscr{X}}$
-modules.
B.2
 ${\mathcal{D}}$
-module on scheme
${\mathcal{D}}$
-module on scheme
Let
![]() $X$
be a scheme smooth over
$X$
be a scheme smooth over
![]() $S$
. Let
$S$
. Let
![]() ${\mathcal{D}}_{X/S}$
be the sheaf of crystalline differential operators on
${\mathcal{D}}_{X/S}$
be the sheaf of crystalline differential operators on
![]() $X$
, i.e.,
$X$
, i.e.,
![]() ${\mathcal{D}}_{X/S}$
is the universal enveloping
${\mathcal{D}}_{X/S}$
is the universal enveloping
![]() ${\mathcal{D}}$
-algebra associated to the relative tangent Lie algebroid
${\mathcal{D}}$
-algebra associated to the relative tangent Lie algebroid
![]() $T_{X/S}$
. By definition, the category of
$T_{X/S}$
. By definition, the category of
![]() ${\mathcal{D}}$
-modules on
${\mathcal{D}}$
-modules on
![]() $X$
is the category of modules over
$X$
is the category of modules over
![]() ${\mathcal{D}}_{X/S}$
that are quasi-coherent as
${\mathcal{D}}_{X/S}$
that are quasi-coherent as
![]() ${\mathcal{O}}_{X}$
-modules. We denote by
${\mathcal{O}}_{X}$
-modules. We denote by
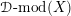 ${\mathcal{D}}\text{-}\text{mod}(X)$
the category of
${\mathcal{D}}\text{-}\text{mod}(X)$
the category of
![]() ${\mathcal{D}}$
-modules on
${\mathcal{D}}$
-modules on
![]() $X$
. In the case
$X$
. In the case
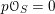 $p{\mathcal{O}}_{S}=0$
, we have the following fundamental observation.
$p{\mathcal{O}}_{S}=0$
, we have the following fundamental observation.
Theorem B.2.1 [Reference Bezrukavnikov, Mirković and RumyninBMR08, §§1.3.2, 2.2.3].
The center of
 $(F_{X/S})_{\ast }{\mathcal{D}}_{X/S}$
is isomorphic to
$(F_{X/S})_{\ast }{\mathcal{D}}_{X/S}$
is isomorphic to
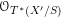 ${\mathcal{O}}_{T^{\ast }(X^{\prime }/S)}$
and there is an Azumaya algebra
${\mathcal{O}}_{T^{\ast }(X^{\prime }/S)}$
and there is an Azumaya algebra
![]() $D_{X/S}$
on
$D_{X/S}$
on
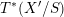 $T^{\ast }(X^{\prime }/S)$
such that
$T^{\ast }(X^{\prime }/S)$
such that
 $$\begin{eqnarray}(F_{X/S})_{\ast }{\mathcal{D}}_{X/S}\simeq (\unicode[STIX]{x1D70F}_{X^{\prime }})_{\ast }D_{X/S}.\end{eqnarray}$$
$$\begin{eqnarray}(F_{X/S})_{\ast }{\mathcal{D}}_{X/S}\simeq (\unicode[STIX]{x1D70F}_{X^{\prime }})_{\ast }D_{X/S}.\end{eqnarray}$$
where
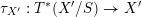 $\unicode[STIX]{x1D70F}_{X^{\prime }}:T^{\ast }(X^{\prime }/S)\rightarrow X^{\prime }$
is the natural projection.
$\unicode[STIX]{x1D70F}_{X^{\prime }}:T^{\ast }(X^{\prime }/S)\rightarrow X^{\prime }$
is the natural projection.
In particular, we have the following.
Corollary B.2.2. There is a canonical equivalence of categories
 $$\begin{eqnarray}{\mathcal{D}}\text{-}\text{mod}(X)\simeq \operatorname{QCoh}(\mathscr{D}_{D_{X/S}})_{1}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{D}}\text{-}\text{mod}(X)\simeq \operatorname{QCoh}(\mathscr{D}_{D_{X/S}})_{1}\end{eqnarray}$$
where
![]() $\mathscr{D}_{D_{X/S}}$
is the gerbe of splittings of
$\mathscr{D}_{D_{X/S}}$
is the gerbe of splittings of
![]() $D_{X/S}$
.
$D_{X/S}$
.
In what follows, the gerbe
![]() $\mathscr{D}_{D_{X/S}}$
will be denoted by
$\mathscr{D}_{D_{X/S}}$
will be denoted by
![]() $\mathscr{D}_{X/S}$
for simplicity.
$\mathscr{D}_{X/S}$
for simplicity.
B.3
 ${\mathcal{D}}$
-module on stack
${\mathcal{D}}$
-module on stack
Let
![]() $S$
be a Noetherian scheme and
$S$
be a Noetherian scheme and
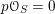 $p{\mathcal{O}}_{S}=0$
. Let
$p{\mathcal{O}}_{S}=0$
. Let
![]() $\mathscr{X}$
be a smooth algebraic stack over
$\mathscr{X}$
be a smooth algebraic stack over
![]() $S$
. A
$S$
. A
![]() ${\mathcal{D}}$
-module
${\mathcal{D}}$
-module
![]() $M$
on
$M$
on
![]() $\mathscr{X}$
is an assignment for each
$\mathscr{X}$
is an assignment for each
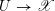 $U\rightarrow \mathscr{X}$
in
$U\rightarrow \mathscr{X}$
in
![]() $\mathscr{X}_{\text{sm}}$
, a
$\mathscr{X}_{\text{sm}}$
, a
![]() ${\mathcal{D}}_{U/S}$
-module
${\mathcal{D}}_{U/S}$
-module
![]() $M_{U}$
and for each morphism
$M_{U}$
and for each morphism
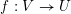 $f:V\rightarrow U$
in
$f:V\rightarrow U$
in
![]() $\mathscr{X}_{\text{sm}}$
an isomorphism
$\mathscr{X}_{\text{sm}}$
an isomorphism
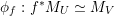 $\unicode[STIX]{x1D719}_{f}:f^{\ast }M_{U}\simeq M_{V}$
which satisfies the cocycle conditions. We denote the category of
$\unicode[STIX]{x1D719}_{f}:f^{\ast }M_{U}\simeq M_{V}$
which satisfies the cocycle conditions. We denote the category of
![]() ${\mathcal{D}}$
-modules on
${\mathcal{D}}$
-modules on
![]() $\mathscr{X}$
by
$\mathscr{X}$
by
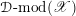 ${\mathcal{D}}\text{-}\text{mod}(\mathscr{X})$
.
${\mathcal{D}}\text{-}\text{mod}(\mathscr{X})$
.
Unlike the case of schemes, in general there does not exist a sheaf of algebras
![]() ${\mathcal{D}}_{\mathscr{X}/S}$
on
${\mathcal{D}}_{\mathscr{X}/S}$
on
![]() $\mathscr{X}$
such that the category of
$\mathscr{X}$
such that the category of
![]() ${\mathcal{D}}$
-modules on
${\mathcal{D}}$
-modules on
![]() $\mathscr{X}$
is equivalent to the category of modules over
$\mathscr{X}$
is equivalent to the category of modules over
![]() ${\mathcal{D}}_{\mathscr{X}/S}$
, and therefore the naive stacky generalization of Theorem B.2.1 is wrong. On the other hand, it is shown in [Reference TravkinTra11] that the obvious stacky version of Corollary B.2.2 is correct.
${\mathcal{D}}_{\mathscr{X}/S}$
, and therefore the naive stacky generalization of Theorem B.2.1 is wrong. On the other hand, it is shown in [Reference TravkinTra11] that the obvious stacky version of Corollary B.2.2 is correct.
Proposition B.3.1. There exists a
![]() $\mathbb{G}_{m}$
-gerbe
$\mathbb{G}_{m}$
-gerbe
![]() $\mathscr{D}_{\mathscr{X}/S}$
on
$\mathscr{D}_{\mathscr{X}/S}$
on
 $T^{\ast }(\mathscr{X}^{\prime }/S)$
such that the category of twisted sheaves on
$T^{\ast }(\mathscr{X}^{\prime }/S)$
such that the category of twisted sheaves on
![]() $\mathscr{D}_{\mathscr{X}/S}$
is equivalent to the category of
$\mathscr{D}_{\mathscr{X}/S}$
is equivalent to the category of
![]() ${\mathcal{D}}$
-modules on
${\mathcal{D}}$
-modules on
![]() $\mathscr{X}$
, i.e., we have
$\mathscr{X}$
, i.e., we have
 $$\begin{eqnarray}{\mathcal{D}}\text{-}\text{mod}(\mathscr{X})\simeq \operatorname{QCoh}(\mathscr{D}_{\mathscr{X}/S})_{1}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{D}}\text{-}\text{mod}(\mathscr{X})\simeq \operatorname{QCoh}(\mathscr{D}_{\mathscr{X}/S})_{1}.\end{eqnarray}$$
Remark B.3.2. It is a theorem of Gabber that on a quasi-projective scheme
![]() $X$
every torsion element in
$X$
every torsion element in
 $\operatorname{H}_{\acute{\text{e}}\text{t}}^{2}(X,\mathbb{G}_{m})$
can be constructed from an Azumaya algebra via (B.1.1). However, this fails for non-separated schemes. A theorem of Töen [Reference ToenToe12] shows that in a very general situation, every
$\operatorname{H}_{\acute{\text{e}}\text{t}}^{2}(X,\mathbb{G}_{m})$
can be constructed from an Azumaya algebra via (B.1.1). However, this fails for non-separated schemes. A theorem of Töen [Reference ToenToe12] shows that in a very general situation, every
![]() $\mathbb{G}_{m}$
-gerbe arises from a derived Azumaya algebra. Although Töen’s theorem does not directly apply to
$\mathbb{G}_{m}$
-gerbe arises from a derived Azumaya algebra. Although Töen’s theorem does not directly apply to
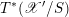 $T^{\ast }(\mathscr{X}^{\prime }/S)$
, it suggests that the derived category of
$T^{\ast }(\mathscr{X}^{\prime }/S)$
, it suggests that the derived category of
![]() ${\mathcal{D}}$
-modules on
${\mathcal{D}}$
-modules on
![]() $\mathscr{X}$
(which is not the derived category of
$\mathscr{X}$
(which is not the derived category of
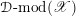 ${\mathcal{D}}\text{-}\text{mod}(\mathscr{X})$
in general) probably should be equivalent to the category of modules over some derived Azumaya algebra
${\mathcal{D}}\text{-}\text{mod}(\mathscr{X})$
in general) probably should be equivalent to the category of modules over some derived Azumaya algebra
![]() $D_{\mathscr{X}/S}^{\text{dr}}$
on
$D_{\mathscr{X}/S}^{\text{dr}}$
on
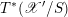 $T^{\ast }(\mathscr{X}^{\prime }/S)$
.
$T^{\ast }(\mathscr{X}^{\prime }/S)$
.
Let us sketch the construction of the
![]() $\mathbb{G}_{m}$
-gerbe
$\mathbb{G}_{m}$
-gerbe
![]() $\mathscr{D}_{\mathscr{X}/S}$
on
$\mathscr{D}_{\mathscr{X}/S}$
on
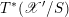 $T^{\ast }(\mathscr{X}^{\prime }/S)$
. As gerbes satisfy smooth descent, it is enough to supply a
$T^{\ast }(\mathscr{X}^{\prime }/S)$
. As gerbes satisfy smooth descent, it is enough to supply a
![]() $\mathbb{G}_{m}$
-gerbe
$\mathbb{G}_{m}$
-gerbe
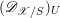 $(\mathscr{D}_{\mathscr{X}/S})_{U}$
on
$(\mathscr{D}_{\mathscr{X}/S})_{U}$
on
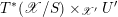 $T^{\ast }(\mathscr{X}/S)\times _{\mathscr{X}^{\prime }}U^{\prime }$
for every
$T^{\ast }(\mathscr{X}/S)\times _{\mathscr{X}^{\prime }}U^{\prime }$
for every
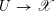 $U\rightarrow \mathscr{X}$
in
$U\rightarrow \mathscr{X}$
in
![]() $\mathscr{X}_{\text{sm}}$
and compatible isomorphisms for any
$\mathscr{X}_{\text{sm}}$
and compatible isomorphisms for any
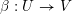 $\unicode[STIX]{x1D6FD}:U\rightarrow V$
in
$\unicode[STIX]{x1D6FD}:U\rightarrow V$
in
![]() $\mathscr{X}_{\text{sm}}$
. But for any
$\mathscr{X}_{\text{sm}}$
. But for any
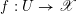 $f:U\rightarrow \mathscr{X}$
in
$f:U\rightarrow \mathscr{X}$
in
![]() $\mathscr{X}_{\text{sm}}$
we have
$\mathscr{X}_{\text{sm}}$
we have
 $$\begin{eqnarray}(f_{U}^{\prime })_{d}:T^{\ast }(\mathscr{X}/S)\times _{\mathscr{ X}^{\prime }}U^{\prime }\rightarrow T^{\ast }(U^{\prime }/S).\end{eqnarray}$$
$$\begin{eqnarray}(f_{U}^{\prime })_{d}:T^{\ast }(\mathscr{X}/S)\times _{\mathscr{ X}^{\prime }}U^{\prime }\rightarrow T^{\ast }(U^{\prime }/S).\end{eqnarray}$$
We have a
![]() $\mathbb{G}_{m}$
-gerbe
$\mathbb{G}_{m}$
-gerbe
![]() $\mathscr{D}_{U/S}$
on
$\mathscr{D}_{U/S}$
on
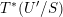 $T^{\ast }(U^{\prime }/S)$
corresponding to the sheaf of relative differential operators
$T^{\ast }(U^{\prime }/S)$
corresponding to the sheaf of relative differential operators
![]() ${\mathcal{D}}_{U/S}$
. We define a
${\mathcal{D}}_{U/S}$
. We define a
![]() $\mathbb{G}_{m}$
-gerbe
$\mathbb{G}_{m}$
-gerbe
 $(\mathscr{D}_{\mathscr{X}/S})_{U}$
on
$(\mathscr{D}_{\mathscr{X}/S})_{U}$
on
 $T^{\ast }(\mathscr{X}/S)\times _{\mathscr{X}^{\prime }}U^{\prime }$
as the pullback of
$T^{\ast }(\mathscr{X}/S)\times _{\mathscr{X}^{\prime }}U^{\prime }$
as the pullback of
![]() $\mathscr{D}_{U/S}$
along
$\mathscr{D}_{U/S}$
along
![]() $(f_{U}^{\prime })_{d}$
. One can check that these gerbes
$(f_{U}^{\prime })_{d}$
. One can check that these gerbes
 $(\mathscr{D}_{\mathscr{X}/S})_{U}$
are compatible under pullbacks, and therefore define a
$(\mathscr{D}_{\mathscr{X}/S})_{U}$
are compatible under pullbacks, and therefore define a
![]() $\mathbb{G}_{m}$
-gerbe
$\mathbb{G}_{m}$
-gerbe
![]() $\mathscr{D}_{\mathscr{X}/S}$
on
$\mathscr{D}_{\mathscr{X}/S}$
on
![]() $\mathscr{X}$
.
$\mathscr{X}$
.
Let
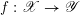 $f:\mathscr{X}\rightarrow \mathscr{Y}$
be a schematic morphism between two smooth algebraic stacks. From the above construction, the following lemma clearly follows from its scheme theoretic version.
$f:\mathscr{X}\rightarrow \mathscr{Y}$
be a schematic morphism between two smooth algebraic stacks. From the above construction, the following lemma clearly follows from its scheme theoretic version.
Lemma B.3.3 [Reference TravkinTra11].
![]() $(1)$
There is a canonical
$(1)$
There is a canonical
![]() $1$
-morphism of
$1$
-morphism of
![]() $\mathbb{G}_{m}$
-gerbe on
$\mathbb{G}_{m}$
-gerbe on
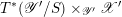 $T^{\ast }(\mathscr{Y}^{\prime }/S)\times _{\mathscr{Y}^{\prime }}\mathscr{X}^{\prime }$
$T^{\ast }(\mathscr{Y}^{\prime }/S)\times _{\mathscr{Y}^{\prime }}\mathscr{X}^{\prime }$
 $$\begin{eqnarray}M_{f}:(f_{p}^{\prime })^{\ast }\mathscr{D}_{\mathscr{ Y}/S}\simeq (f_{d}^{\prime })^{\ast }\mathscr{D}_{\mathscr{ X}/S}.\end{eqnarray}$$
$$\begin{eqnarray}M_{f}:(f_{p}^{\prime })^{\ast }\mathscr{D}_{\mathscr{ Y}/S}\simeq (f_{d}^{\prime })^{\ast }\mathscr{D}_{\mathscr{ X}/S}.\end{eqnarray}$$
![]() $(2)$
For a pair of morphisms
$(2)$
For a pair of morphisms
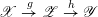 $\mathscr{X}\stackrel{g}{\rightarrow }\mathscr{Z}\stackrel{h}{\rightarrow }\mathscr{Y}$
and their composition
$\mathscr{X}\stackrel{g}{\rightarrow }\mathscr{Z}\stackrel{h}{\rightarrow }\mathscr{Y}$
and their composition
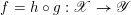 $f=h\circ g:\mathscr{X}\rightarrow \mathscr{Y}$
, there is a canonical
$f=h\circ g:\mathscr{X}\rightarrow \mathscr{Y}$
, there is a canonical
![]() $1$
-morphisms of
$1$
-morphisms of
![]() $\mathbb{G}_{m}$
-gerbe on
$\mathbb{G}_{m}$
-gerbe on
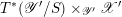 $T^{\ast }(\mathscr{Y}^{\prime }/S)\times _{\mathscr{Y}^{\prime }}\mathscr{X}^{\prime }$
$T^{\ast }(\mathscr{Y}^{\prime }/S)\times _{\mathscr{Y}^{\prime }}\mathscr{X}^{\prime }$
 $$\begin{eqnarray}M_{g,h}:(f_{p}^{\prime })^{\ast }\mathscr{D}_{\mathscr{ Y}/S}\simeq (f_{d}^{\prime })^{\ast }\mathscr{D}_{\mathscr{ X}/S},\end{eqnarray}$$
$$\begin{eqnarray}M_{g,h}:(f_{p}^{\prime })^{\ast }\mathscr{D}_{\mathscr{ Y}/S}\simeq (f_{d}^{\prime })^{\ast }\mathscr{D}_{\mathscr{ X}/S},\end{eqnarray}$$
together with a canonical
![]() $2$
-morphism between
$2$
-morphism between
![]() $M_{h\circ g}$
and
$M_{h\circ g}$
and
![]() $M_{g,h}$
.
$M_{g,h}$
.
![]() $(3)$
We have a canonical
$(3)$
We have a canonical
![]() $1$
-morphism of
$1$
-morphism of
![]() $\mathbb{G}_{m}$
-gerbe on
$\mathbb{G}_{m}$
-gerbe on
 $T^{\ast }(\mathscr{X}^{\prime }/S)^{\text{sm}}$
:
$T^{\ast }(\mathscr{X}^{\prime }/S)^{\text{sm}}$
:
 $$\begin{eqnarray}\mathscr{D}_{\mathscr{X}/S}|_{T^{\ast }(\mathscr{X}^{\prime }/S)^{\text{sm}}}\simeq \mathscr{D}_{T^{\ast }(\mathscr{X}^{\prime }/S)^{\text{sm}}/S}(\unicode[STIX]{x1D703}_{\text{can}}):=\unicode[STIX]{x1D703}_{\text{can}}^{\ast }(\mathscr{D}_{T^{\ast }(\mathscr{X}^{\prime }/S)^{\text{sm}}/S}),\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{D}_{\mathscr{X}/S}|_{T^{\ast }(\mathscr{X}^{\prime }/S)^{\text{sm}}}\simeq \mathscr{D}_{T^{\ast }(\mathscr{X}^{\prime }/S)^{\text{sm}}/S}(\unicode[STIX]{x1D703}_{\text{can}}):=\unicode[STIX]{x1D703}_{\text{can}}^{\ast }(\mathscr{D}_{T^{\ast }(\mathscr{X}^{\prime }/S)^{\text{sm}}/S}),\end{eqnarray}$$
where
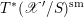 $T^{\ast }(\mathscr{X}^{\prime }/S)^{\text{sm}}$
is the maximal smooth open substack of
$T^{\ast }(\mathscr{X}^{\prime }/S)^{\text{sm}}$
is the maximal smooth open substack of
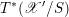 $T^{\ast }(\mathscr{X}^{\prime }/S)$
and
$T^{\ast }(\mathscr{X}^{\prime }/S)$
and
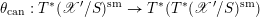 $\unicode[STIX]{x1D703}_{\text{can}}:T^{\ast }(\mathscr{X}^{\prime }/S)^{\text{sm}}\rightarrow T^{\ast }(T^{\ast }(\mathscr{X}^{\prime }/S)^{\text{sm}})$
is the canonical one form.
$\unicode[STIX]{x1D703}_{\text{can}}:T^{\ast }(\mathscr{X}^{\prime }/S)^{\text{sm}}\rightarrow T^{\ast }(T^{\ast }(\mathscr{X}^{\prime }/S)^{\text{sm}})$
is the canonical one form.
Let us discuss a stacky version of [Reference Ogus and VologodskyOV07, §4.3]. Let
![]() $\mathscr{X}/S$
be a smooth algebraic stack as above and let
$\mathscr{X}/S$
be a smooth algebraic stack as above and let
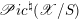 $\mathscr{P}ic^{\natural }(\mathscr{X}/S)$
be the Picard stack of invertible sheaves on
$\mathscr{P}ic^{\natural }(\mathscr{X}/S)$
be the Picard stack of invertible sheaves on
![]() $\mathscr{X}$
equipped with a connection (i.e., objects in
$\mathscr{X}$
equipped with a connection (i.e., objects in
 $\mathscr{P}ic^{\natural }(\mathscr{X}/S)$
are
$\mathscr{P}ic^{\natural }(\mathscr{X}/S)$
are
![]() ${\mathcal{D}}$
-modules on
${\mathcal{D}}$
-modules on
![]() $\mathscr{X}$
whose underlying quasi-coherent sheaves are invertible). Let
$\mathscr{X}$
whose underlying quasi-coherent sheaves are invertible). Let
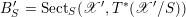 $B_{S}^{\prime }=\operatorname{Sect}_{S}(\mathscr{X}^{\prime },T^{\ast }(\mathscr{X}^{\prime }/S))$
. Note that the following proposition does not need the representability of
$B_{S}^{\prime }=\operatorname{Sect}_{S}(\mathscr{X}^{\prime },T^{\ast }(\mathscr{X}^{\prime }/S))$
. Note that the following proposition does not need the representability of
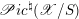 $\mathscr{P}ic^{\natural }(\mathscr{X}/S)$
.
$\mathscr{P}ic^{\natural }(\mathscr{X}/S)$
.
Proposition B.3.4.
-
(1) There is a natural morphism
 $\unicode[STIX]{x1D713}:\mathscr{P}ic^{\natural }(\mathscr{X}/S)\rightarrow B_{S}^{\prime }$
.
$\unicode[STIX]{x1D713}:\mathscr{P}ic^{\natural }(\mathscr{X}/S)\rightarrow B_{S}^{\prime }$
. -
(2) The pullback of the gerbe
 $\mathscr{D}_{\mathscr{X}/S}$
along is canonically trivialized.
$\mathscr{D}_{\mathscr{X}/S}$
along is canonically trivialized. $$\begin{eqnarray}\mathscr{X}^{\prime }\times _{S}\mathscr{P}ic^{\natural }(\mathscr{X}/S)\stackrel{\operatorname{id}\times \unicode[STIX]{x1D713}}{\rightarrow }\mathscr{X}^{\prime }\times _{S}B_{S}^{\prime }\rightarrow T^{\ast }(\mathscr{X}^{\prime }/S)\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{X}^{\prime }\times _{S}\mathscr{P}ic^{\natural }(\mathscr{X}/S)\stackrel{\operatorname{id}\times \unicode[STIX]{x1D713}}{\rightarrow }\mathscr{X}^{\prime }\times _{S}B_{S}^{\prime }\rightarrow T^{\ast }(\mathscr{X}^{\prime }/S)\end{eqnarray}$$
Proof. For part (1), recall that if
![]() $\mathscr{X}$
is a scheme, the morphism
$\mathscr{X}$
is a scheme, the morphism
![]() $\unicode[STIX]{x1D713}$
is given by the
$\unicode[STIX]{x1D713}$
is given by the
![]() $p$
-curvature map (see [Reference Ogus and VologodskyOV07, §4.3]). We explain how to generalize this map to stacks. Let
$p$
-curvature map (see [Reference Ogus and VologodskyOV07, §4.3]). We explain how to generalize this map to stacks. Let
 $U\rightarrow \mathscr{X}$
be a smooth morphism. Then via pullback, we obtain a morphism
$U\rightarrow \mathscr{X}$
be a smooth morphism. Then via pullback, we obtain a morphism
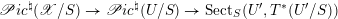 $\mathscr{P}ic^{\natural }(\mathscr{X}/S)\rightarrow \mathscr{P}ic^{\natural }(U/S)\rightarrow \operatorname{Sect}_{S}(U^{\prime },T^{\ast }(U^{\prime }/S))$
. By considering further pullbacks to
$\mathscr{P}ic^{\natural }(\mathscr{X}/S)\rightarrow \mathscr{P}ic^{\natural }(U/S)\rightarrow \operatorname{Sect}_{S}(U^{\prime },T^{\ast }(U^{\prime }/S))$
. By considering further pullbacks to
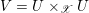 $V=U\times _{\mathscr{X}}U$
, we find that the above maps fit into the following commutative diagram.
$V=U\times _{\mathscr{X}}U$
, we find that the above maps fit into the following commutative diagram.

These
![]() $\unicode[STIX]{x1D713}_{U}$
are compatible under pullbacks and define the
$\unicode[STIX]{x1D713}_{U}$
are compatible under pullbacks and define the
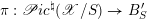 $\unicode[STIX]{x1D70B}:\mathscr{P}ic^{\natural }(\mathscr{X}/S)\rightarrow B_{S}^{\prime }$
.
$\unicode[STIX]{x1D70B}:\mathscr{P}ic^{\natural }(\mathscr{X}/S)\rightarrow B_{S}^{\prime }$
.
For part (2), again let
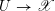 $U\rightarrow \mathscr{X}$
be a smooth morphism. Note that the pullback of the gerbe
$U\rightarrow \mathscr{X}$
be a smooth morphism. Note that the pullback of the gerbe
![]() $\mathscr{D}_{U/S}$
along
$\mathscr{D}_{U/S}$
along
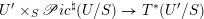 $U^{\prime }\times _{S}\mathscr{P}ic^{\natural }(U/S)\rightarrow T^{\ast }(U^{\prime }/S)$
is canonically trivialized by the object
$U^{\prime }\times _{S}\mathscr{P}ic^{\natural }(U/S)\rightarrow T^{\ast }(U^{\prime }/S)$
is canonically trivialized by the object
 $F_{\ast }({\mathcal{L}},\unicode[STIX]{x1D6FB})$
, where
$F_{\ast }({\mathcal{L}},\unicode[STIX]{x1D6FB})$
, where
![]() $({\mathcal{L}},\unicode[STIX]{x1D6FB})$
is the universal object on
$({\mathcal{L}},\unicode[STIX]{x1D6FB})$
is the universal object on
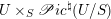 $U\times _{S}\mathscr{P}ic^{\natural }(U/S)$
. Combining this with Lemma B.3.3 and the proof of part (1), this shows that the pullback of
$U\times _{S}\mathscr{P}ic^{\natural }(U/S)$
. Combining this with Lemma B.3.3 and the proof of part (1), this shows that the pullback of
![]() $\mathscr{D}_{\mathscr{X}/S}$
along
$\mathscr{D}_{\mathscr{X}/S}$
along
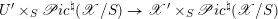 $U^{\prime }\times _{S}\mathscr{P}ic^{\natural }(\mathscr{X}/S)\rightarrow \mathscr{X}^{\prime }\times _{S}\mathscr{P}ic^{\natural }(\mathscr{X}/S)$
is canonically trivialized. These trivializations glue together and give a canonical trivialization of
$U^{\prime }\times _{S}\mathscr{P}ic^{\natural }(\mathscr{X}/S)\rightarrow \mathscr{X}^{\prime }\times _{S}\mathscr{P}ic^{\natural }(\mathscr{X}/S)$
is canonically trivialized. These trivializations glue together and give a canonical trivialization of
![]() $\mathscr{D}_{\mathscr{X}/S}$
on
$\mathscr{D}_{\mathscr{X}/S}$
on
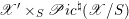 $\mathscr{X}^{\prime }\times _{S}\mathscr{P}ic^{\natural }(\mathscr{X}/S)$
.◻
$\mathscr{X}^{\prime }\times _{S}\mathscr{P}ic^{\natural }(\mathscr{X}/S)$
.◻
B.4 1-forms
In this subsection we make a digression into the construction of gerbes using 1-forms. We refer to [Reference Chen and ZhuCZ15, Appendix A.8] for more details. Recall that for any smooth algebraic stack
![]() $\mathscr{X}/S$
we can associate to it a
$\mathscr{X}/S$
we can associate to it a
![]() $\mathbb{G}_{m}$
-gerbe
$\mathbb{G}_{m}$
-gerbe
![]() $\mathscr{D}_{\mathscr{X}/S}$
on
$\mathscr{D}_{\mathscr{X}/S}$
on
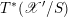 $T^{\ast }(\mathscr{X}^{\prime }/S)$
. Thus giving a 1-form
$T^{\ast }(\mathscr{X}^{\prime }/S)$
. Thus giving a 1-form
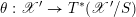 $\unicode[STIX]{x1D703}:\mathscr{X}^{\prime }\rightarrow T^{\ast }(\mathscr{X}^{\prime }/S)$
we can construct a
$\unicode[STIX]{x1D703}:\mathscr{X}^{\prime }\rightarrow T^{\ast }(\mathscr{X}^{\prime }/S)$
we can construct a
![]() $\mathbb{G}_{m}$
-gerbe
$\mathbb{G}_{m}$
-gerbe
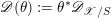 $\mathscr{D}(\unicode[STIX]{x1D703}):=\unicode[STIX]{x1D703}^{\ast }\mathscr{D}_{\mathscr{X}/S}$
on
$\mathscr{D}(\unicode[STIX]{x1D703}):=\unicode[STIX]{x1D703}^{\ast }\mathscr{D}_{\mathscr{X}/S}$
on
![]() $\mathscr{X}^{\prime }$
by pulling back
$\mathscr{X}^{\prime }$
by pulling back
![]() $\mathscr{D}_{\mathscr{X}/S}$
along
$\mathscr{D}_{\mathscr{X}/S}$
along
![]() $\unicode[STIX]{x1D703}$
.
$\unicode[STIX]{x1D703}$
.
When
 $\mathscr{X}=X$
is a smooth Noetherian scheme, above construction can be generalized as follows. Let
$\mathscr{X}=X$
is a smooth Noetherian scheme, above construction can be generalized as follows. Let
![]() ${\mathcal{G}}$
be a smooth affine commutative group scheme over
${\mathcal{G}}$
be a smooth affine commutative group scheme over
![]() $X$
. For any section
$X$
. For any section
![]() $\unicode[STIX]{x1D703}$
of
$\unicode[STIX]{x1D703}$
of
 $\operatorname{Lie}\,{\mathcal{G}}^{\prime }\otimes \unicode[STIX]{x1D6FA}_{X^{\prime }/S}$
we can associate to it a
$\operatorname{Lie}\,{\mathcal{G}}^{\prime }\otimes \unicode[STIX]{x1D6FA}_{X^{\prime }/S}$
we can associate to it a
![]() ${\mathcal{G}}$
-gerbe
${\mathcal{G}}$
-gerbe
![]() $\mathscr{D}(\unicode[STIX]{x1D703})$
on
$\mathscr{D}(\unicode[STIX]{x1D703})$
on
![]() $X^{\prime }$
using the four term exact sequence constructed in loc. cit. In the case
$X^{\prime }$
using the four term exact sequence constructed in loc. cit. In the case
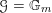 ${\mathcal{G}}=\mathbb{G}_{m}$
, the
${\mathcal{G}}=\mathbb{G}_{m}$
, the
![]() $\mathbb{G}_{m}$
-gerbe
$\mathbb{G}_{m}$
-gerbe
![]() $\mathscr{D}(\unicode[STIX]{x1D703})$
is isomorphic to
$\mathscr{D}(\unicode[STIX]{x1D703})$
is isomorphic to
![]() $\unicode[STIX]{x1D703}^{\ast }\mathscr{D}_{X,S}$
the pullback of
$\unicode[STIX]{x1D703}^{\ast }\mathscr{D}_{X,S}$
the pullback of
![]() $\mathscr{D}_{X/S}$
along
$\mathscr{D}_{X/S}$
along
 $\unicode[STIX]{x1D703}:\mathscr{X}^{\prime }\rightarrow T^{\ast }(X^{\prime }/S)$
. We have the following functorial properties.
$\unicode[STIX]{x1D703}:\mathscr{X}^{\prime }\rightarrow T^{\ast }(X^{\prime }/S)$
. We have the following functorial properties.
Lemma B.4.1.
![]() $(1)$
Let
$(1)$
Let
![]() $\mathscr{Y}$
be another smooth algebraic stack over
$\mathscr{Y}$
be another smooth algebraic stack over
![]() $S$
and let
$S$
and let
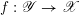 $f:\mathscr{Y}\rightarrow \mathscr{X}$
be a morphism. Let
$f:\mathscr{Y}\rightarrow \mathscr{X}$
be a morphism. Let
![]() $\unicode[STIX]{x1D703}$
be a
$\unicode[STIX]{x1D703}$
be a
![]() $1$
-form on
$1$
-form on
![]() $\mathscr{X}$
. There is a canonical equivalence of
$\mathscr{X}$
. There is a canonical equivalence of
![]() $\mathbb{G}_{m}$
-gerbes on
$\mathbb{G}_{m}$
-gerbes on
![]() $\mathscr{Y}^{\prime }$
$\mathscr{Y}^{\prime }$
 $$\begin{eqnarray}{f^{\prime }}^{\ast }\mathscr{D}(\unicode[STIX]{x1D703})\simeq \mathscr{D}({f^{\prime }}^{\ast }\unicode[STIX]{x1D703}).\end{eqnarray}$$
$$\begin{eqnarray}{f^{\prime }}^{\ast }\mathscr{D}(\unicode[STIX]{x1D703})\simeq \mathscr{D}({f^{\prime }}^{\ast }\unicode[STIX]{x1D703}).\end{eqnarray}$$
![]() $(2)$
Let
$(2)$
Let
![]() $X$
be a smooth Noetherian scheme and let
$X$
be a smooth Noetherian scheme and let
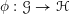 $\unicode[STIX]{x1D719}:{\mathcal{G}}\rightarrow {\mathcal{H}}$
be a morphism of smooth commutative affine group schemes over
$\unicode[STIX]{x1D719}:{\mathcal{G}}\rightarrow {\mathcal{H}}$
be a morphism of smooth commutative affine group schemes over
![]() $X$
. For any section
$X$
. For any section
![]() $\unicode[STIX]{x1D703}$
of
$\unicode[STIX]{x1D703}$
of
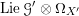 $\operatorname{Lie}\,{\mathcal{G}}^{\prime }\otimes \unicode[STIX]{x1D6FA}_{X^{\prime }}$
let
$\operatorname{Lie}\,{\mathcal{G}}^{\prime }\otimes \unicode[STIX]{x1D6FA}_{X^{\prime }}$
let
![]() $\unicode[STIX]{x1D719}_{\ast }^{\prime }\unicode[STIX]{x1D703}$
denote its image
$\unicode[STIX]{x1D719}_{\ast }^{\prime }\unicode[STIX]{x1D703}$
denote its image
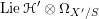 $\operatorname{Lie}\,{\mathcal{H}}^{\prime }\otimes \unicode[STIX]{x1D6FA}_{X^{\prime }/S}$
under the map induced by
$\operatorname{Lie}\,{\mathcal{H}}^{\prime }\otimes \unicode[STIX]{x1D6FA}_{X^{\prime }/S}$
under the map induced by
![]() $\unicode[STIX]{x1D719}$
. There is a canonical equivalence of
$\unicode[STIX]{x1D719}$
. There is a canonical equivalence of
![]() ${\mathcal{H}}^{\prime }$
-gerbes on
${\mathcal{H}}^{\prime }$
-gerbes on
![]() $X^{\prime }$
,
$X^{\prime }$
,
 $$\begin{eqnarray}\mathscr{D}(\unicode[STIX]{x1D703})^{\unicode[STIX]{x1D719}^{\prime }}\simeq \mathscr{D}(\unicode[STIX]{x1D719}_{\ast }^{\prime }\unicode[STIX]{x1D703}),\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{D}(\unicode[STIX]{x1D703})^{\unicode[STIX]{x1D719}^{\prime }}\simeq \mathscr{D}(\unicode[STIX]{x1D719}_{\ast }^{\prime }\unicode[STIX]{x1D703}),\end{eqnarray}$$
where
![]() $\mathscr{D}(\unicode[STIX]{x1D703})^{\unicode[STIX]{x1D719}^{\prime }}$
is the
$\mathscr{D}(\unicode[STIX]{x1D703})^{\unicode[STIX]{x1D719}^{\prime }}$
is the
![]() ${\mathcal{H}}^{\prime }$
-gerbe induced form
${\mathcal{H}}^{\prime }$
-gerbe induced form
![]() $\mathscr{D}(\unicode[STIX]{x1D703})$
using the map
$\mathscr{D}(\unicode[STIX]{x1D703})$
using the map
![]() $\unicode[STIX]{x1D719}^{\prime }$
(see §A.6).
$\unicode[STIX]{x1D719}^{\prime }$
(see §A.6).
B.5 Azumaya property of differential operators on good stacks
Recall that a smooth algebraic stack
![]() $\mathscr{X}$
over
$\mathscr{X}$
over
![]() $S$
of relative dimension
$S$
of relative dimension
![]() $d$
is called relatively good if it satisfies the following equivalent properties:
$d$
is called relatively good if it satisfies the following equivalent properties:
-
(1)
 $\operatorname{dim}(T^{\ast }(\mathscr{X}/S))=2d$
;
$\operatorname{dim}(T^{\ast }(\mathscr{X}/S))=2d$
; -
(2)
 $\operatorname{codim}\{x\in \mathscr{X}|\operatorname{dim}\operatorname{Aut}(x)=n\}\geqslant n$
for all
$\operatorname{codim}\{x\in \mathscr{X}|\operatorname{dim}\operatorname{Aut}(x)=n\}\geqslant n$
for all
 $n>0$
;
$n>0$
; -
(3) for any
 $U\rightarrow \mathscr{X}$
in
$U\rightarrow \mathscr{X}$
in
 $\mathscr{X}_{\text{sm}}$
, the complex has cohomology concentrated in degree
$\mathscr{X}_{\text{sm}}$
, the complex has cohomology concentrated in degree $$\begin{eqnarray}\operatorname{Sym}(T_{U/\mathscr{X}}\rightarrow T_{U/S})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Sym}(T_{U/\mathscr{X}}\rightarrow T_{U/S})\end{eqnarray}$$
 $0$
and
$0$
and  $$\begin{eqnarray}H^{0}(\operatorname{Sym}(T_{U/\mathscr{X}}\rightarrow T_{U/S}))\simeq \operatorname{Sym}(T_{U/S})/T_{U/\mathscr{X}}\operatorname{Sym}(T_{U/S}).\end{eqnarray}$$
$$\begin{eqnarray}H^{0}(\operatorname{Sym}(T_{U/\mathscr{X}}\rightarrow T_{U/S}))\simeq \operatorname{Sym}(T_{U/S})/T_{U/\mathscr{X}}\operatorname{Sym}(T_{U/S}).\end{eqnarray}$$
The following proposition is proved in [Reference Bezrukavnikov and BravermanBB07] (see also [Reference TravkinTra11]).
Proposition B.5.1. Let
![]() $\mathscr{X}$
be a relatively good stack. Let
$\mathscr{X}$
be a relatively good stack. Let
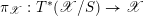 $\unicode[STIX]{x1D70B}_{\mathscr{X}}:T^{\ast }(\mathscr{X}/S)\rightarrow \mathscr{X}$
be the natural projection and
$\unicode[STIX]{x1D70B}_{\mathscr{X}}:T^{\ast }(\mathscr{X}/S)\rightarrow \mathscr{X}$
be the natural projection and
![]() $\unicode[STIX]{x1D70B}_{\mathscr{X}^{\prime }}$
be its Frobenius twist. Let
$\unicode[STIX]{x1D70B}_{\mathscr{X}^{\prime }}$
be its Frobenius twist. Let
 $T^{\ast }(\mathscr{X}^{\prime }/S)^{0}$
be the maximal smooth open substack of
$T^{\ast }(\mathscr{X}^{\prime }/S)^{0}$
be the maximal smooth open substack of
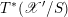 $T^{\ast }(\mathscr{X}^{\prime }/S)$
. Then we have the following.
$T^{\ast }(\mathscr{X}^{\prime }/S)$
. Then we have the following.
-
(i) There is a natural coherent sheaf of algebras
 $D_{\mathscr{X}/S}$
on
$D_{\mathscr{X}/S}$
on
 $T^{\ast }(\mathscr{X}^{\prime }/S)$
such that the restriction of
$T^{\ast }(\mathscr{X}^{\prime }/S)$
such that the restriction of
 $D_{\mathscr{X}/S}$
to
$D_{\mathscr{X}/S}$
to
 $T^{\ast }(\mathscr{X}^{\prime }/S)^{0}$
is an Azumaya algebra on
$T^{\ast }(\mathscr{X}^{\prime }/S)^{0}$
is an Azumaya algebra on
 $T^{\ast }(\mathscr{X}^{\prime }/S)^{0}$
of rank
$T^{\ast }(\mathscr{X}^{\prime }/S)^{0}$
of rank
 $p^{2\operatorname{dim}(\mathscr{X}/S)}$
.
$p^{2\operatorname{dim}(\mathscr{X}/S)}$
. -
(ii) The
 $\mathbb{G}_{m}$
-gerbe
$\mathbb{G}_{m}$
-gerbe
 $\mathscr{D}_{\mathscr{X}/S}^{0}:=\mathscr{D}_{\mathscr{X}/S}|_{T^{\ast }(\mathscr{X}^{\prime }/S)^{0}}$
is isomorphic to
$\mathscr{D}_{\mathscr{X}/S}^{0}:=\mathscr{D}_{\mathscr{X}/S}|_{T^{\ast }(\mathscr{X}^{\prime }/S)^{0}}$
is isomorphic to
 $\mathscr{D}_{D_{\mathscr{X}/S}^{0}}$
, the gerbe of splittings of
$\mathscr{D}_{D_{\mathscr{X}/S}^{0}}$
, the gerbe of splittings of
 $D_{\mathscr{X}/S}^{0}$
. In particular, we have
$D_{\mathscr{X}/S}^{0}$
. In particular, we have  $$\begin{eqnarray}D_{\mathscr{X}/S}^{0}\text{-}\text{mod}\simeq \operatorname{QCoh}(\mathscr{D}_{\mathscr{ X}/S}^{0})_{1}.\end{eqnarray}$$
$$\begin{eqnarray}D_{\mathscr{X}/S}^{0}\text{-}\text{mod}\simeq \operatorname{QCoh}(\mathscr{D}_{\mathscr{ X}/S}^{0})_{1}.\end{eqnarray}$$
Remark B.5.2. By Proposition B.3.1, the category
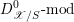 $D_{\mathscr{X}/S}^{0}\text{-}\text{mod}$
can be thought as a localization of the category of
$D_{\mathscr{X}/S}^{0}\text{-}\text{mod}$
can be thought as a localization of the category of
![]() ${\mathcal{D}}$
-modules on
${\mathcal{D}}$
-modules on
![]() $\mathscr{X}$
.
$\mathscr{X}$
.
Appendix C Abelian duality
C.1 Abelian duality for Beilinson 1-motives
Assume that
![]() $S$
is a scheme and
$S$
is a scheme and
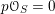 $p{\mathcal{O}}_{S}=0$
. Let
$p{\mathcal{O}}_{S}=0$
. Let
![]() $\mathscr{A}$
be a Picard stack over
$\mathscr{A}$
be a Picard stack over
![]() $S$
. In this subsection, we denote the base change of
$S$
. In this subsection, we denote the base change of
![]() $\mathscr{A}$
along
$\mathscr{A}$
along
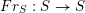 $Fr_{S}:S\rightarrow S$
by
$Fr_{S}:S\rightarrow S$
by
![]() $\mathscr{A}^{\prime }$
instead of
$\mathscr{A}^{\prime }$
instead of
![]() $\mathscr{A}^{(S)}$
. Let
$\mathscr{A}^{(S)}$
. Let
![]() $\mathbb{T}_{e}^{\ast }\mathscr{A}^{\prime }$
be the vector bundle on
$\mathbb{T}_{e}^{\ast }\mathscr{A}^{\prime }$
be the vector bundle on
![]() $S$
, which is the restriction of the relative (to
$S$
, which is the restriction of the relative (to
![]() $S$
) cotangent bundle of
$S$
) cotangent bundle of
![]() $\mathscr{A}^{\prime }$
along
$\mathscr{A}^{\prime }$
along
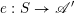 $e:S\rightarrow \mathscr{A}^{\prime }$
. Then there is a canonical isomorphism
$e:S\rightarrow \mathscr{A}^{\prime }$
. Then there is a canonical isomorphism
 $$\begin{eqnarray}\mathscr{A}^{\prime }\times _{S}\mathbb{T}_{e}^{\ast }\mathscr{A}^{\prime }\simeq T^{\ast }(\mathscr{A}^{\prime }/S).\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{A}^{\prime }\times _{S}\mathbb{T}_{e}^{\ast }\mathscr{A}^{\prime }\simeq T^{\ast }(\mathscr{A}^{\prime }/S).\end{eqnarray}$$
Therefore, via the map
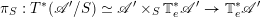 $\unicode[STIX]{x1D70B}_{S}:T^{\ast }(\mathscr{A}^{\prime }/S)\simeq \mathscr{A}^{\prime }\times _{S}\mathbb{T}_{e}^{\ast }\mathscr{A}^{\prime }\rightarrow \mathbb{T}_{e}^{\ast }\mathscr{A}^{\prime }$
,
$\unicode[STIX]{x1D70B}_{S}:T^{\ast }(\mathscr{A}^{\prime }/S)\simeq \mathscr{A}^{\prime }\times _{S}\mathbb{T}_{e}^{\ast }\mathscr{A}^{\prime }\rightarrow \mathbb{T}_{e}^{\ast }\mathscr{A}^{\prime }$
,
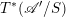 $T^{\ast }(\mathscr{A}^{\prime }/S)$
becomes a Picard stack over
$T^{\ast }(\mathscr{A}^{\prime }/S)$
becomes a Picard stack over
![]() $\mathbb{T}_{e}^{\ast }\mathscr{A}^{\prime }$
and we denote by
$\mathbb{T}_{e}^{\ast }\mathscr{A}^{\prime }$
and we denote by
![]() $m_{S}$
the multiplication map:
$m_{S}$
the multiplication map:
 $$\begin{eqnarray}m_{S}:T^{\ast }(\mathscr{A}^{\prime }/S)\times _{\mathbb{ T}_{e}^{\ast }\mathscr{A}^{\prime }}T^{\ast }(\mathscr{A}^{\prime }/S)\rightarrow T^{\ast }(\mathscr{A}^{\prime }/S).\end{eqnarray}$$
$$\begin{eqnarray}m_{S}:T^{\ast }(\mathscr{A}^{\prime }/S)\times _{\mathbb{ T}_{e}^{\ast }\mathscr{A}^{\prime }}T^{\ast }(\mathscr{A}^{\prime }/S)\rightarrow T^{\ast }(\mathscr{A}^{\prime }/S).\end{eqnarray}$$
Recall that it makes sense to talk about a gerbe on a Picard stack with a commutative group structure (cf. Definition A.5.2).
Lemma C.1.1. The gerbe
![]() $\mathscr{D}_{\mathscr{A}/S}$
on
$\mathscr{D}_{\mathscr{A}/S}$
on
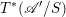 $T^{\ast }(\mathscr{A}^{\prime }/S)$
admits a canonical commutative group structure.
$T^{\ast }(\mathscr{A}^{\prime }/S)$
admits a canonical commutative group structure.
Proof. Let us sketch the construction of the multiplicative structure
![]() $M$
and the
$M$
and the
![]() $2$
-morphisms
$2$
-morphisms
![]() $\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FE}$
and
![]() $i$
in Definition A.5.2. The multiplication
$i$
in Definition A.5.2. The multiplication
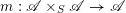 $m:\mathscr{A}\times _{S}\mathscr{A}\rightarrow \mathscr{A}$
induces the following diagram.
$m:\mathscr{A}\times _{S}\mathscr{A}\rightarrow \mathscr{A}$
induces the following diagram.

Observe that the map
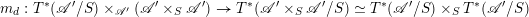 $m_{d}:T^{\ast }(\mathscr{A}^{\prime }/S)\times _{\mathscr{A}^{\prime }}(\mathscr{A}^{\prime }\times _{S}\mathscr{A}^{\prime })\rightarrow T^{\ast }(\mathscr{A}^{\prime }\times _{S}\mathscr{A}^{\prime }/S)\simeq T^{\ast }(\mathscr{A}^{\prime }/S)\times _{S}T^{\ast }(\mathscr{A}^{\prime }/S)$
induces an isomorphism
$m_{d}:T^{\ast }(\mathscr{A}^{\prime }/S)\times _{\mathscr{A}^{\prime }}(\mathscr{A}^{\prime }\times _{S}\mathscr{A}^{\prime })\rightarrow T^{\ast }(\mathscr{A}^{\prime }\times _{S}\mathscr{A}^{\prime }/S)\simeq T^{\ast }(\mathscr{A}^{\prime }/S)\times _{S}T^{\ast }(\mathscr{A}^{\prime }/S)$
induces an isomorphism
 $$\begin{eqnarray}T^{\ast }(\mathscr{A}^{\prime }/S)\times _{\mathscr{ A}^{\prime }}(\mathscr{A}^{\prime }\times _{S}\mathscr{A}^{\prime })\simeq T^{\ast }(\mathscr{A}^{\prime }/S)\times _{\mathbb{ T}_{e}^{\ast }\mathscr{A}^{\prime }}T^{\ast }(\mathscr{A}^{\prime }/S)\rightarrow T^{\ast }(\mathscr{A}^{\prime }/S)\times _{S}T^{\ast }(\mathscr{A}^{\prime }/S).\end{eqnarray}$$
$$\begin{eqnarray}T^{\ast }(\mathscr{A}^{\prime }/S)\times _{\mathscr{ A}^{\prime }}(\mathscr{A}^{\prime }\times _{S}\mathscr{A}^{\prime })\simeq T^{\ast }(\mathscr{A}^{\prime }/S)\times _{\mathbb{ T}_{e}^{\ast }\mathscr{A}^{\prime }}T^{\ast }(\mathscr{A}^{\prime }/S)\rightarrow T^{\ast }(\mathscr{A}^{\prime }/S)\times _{S}T^{\ast }(\mathscr{A}^{\prime }/S).\end{eqnarray}$$
Under this isomorphism
![]() $m_{p}$
becomes the multiplication map
$m_{p}$
becomes the multiplication map
![]() $m_{S}$
. Now the canonical
$m_{S}$
. Now the canonical
![]() $1$
-morphism between
$1$
-morphism between
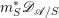 $m_{S}^{\ast }\mathscr{D}_{\mathscr{A}/S}$
and
$m_{S}^{\ast }\mathscr{D}_{\mathscr{A}/S}$
and
 $\mathscr{D}_{\mathscr{A}/S}\boxtimes \mathscr{D}_{\mathscr{A}/S}$
comes from Lemma B.3.3. We have two different factorizations of the multiplicative morphism
$\mathscr{D}_{\mathscr{A}/S}\boxtimes \mathscr{D}_{\mathscr{A}/S}$
comes from Lemma B.3.3. We have two different factorizations of the multiplicative morphism
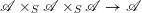 $\mathscr{A}\times _{S}\mathscr{A}\times _{S}\mathscr{A}\rightarrow \mathscr{A}$
and the
$\mathscr{A}\times _{S}\mathscr{A}\times _{S}\mathscr{A}\rightarrow \mathscr{A}$
and the
![]() $2$
-morphisms
$2$
-morphisms
![]() $\unicode[STIX]{x1D6FE}$
comes from the
$\unicode[STIX]{x1D6FE}$
comes from the
![]() $2$
-morphisms for corresponding equivalences of Lemma B.3.3. Finally, the
$2$
-morphisms for corresponding equivalences of Lemma B.3.3. Finally, the
![]() $2$
-morphism
$2$
-morphism
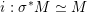 $i:\unicode[STIX]{x1D70E}^{\ast }M\simeq M$
can be constructed by applying Lemma B.3.3 to the morphism
$i:\unicode[STIX]{x1D70E}^{\ast }M\simeq M$
can be constructed by applying Lemma B.3.3 to the morphism
 $\mathscr{A}\times _{S}\mathscr{A}\stackrel{\unicode[STIX]{x1D70E}}{\rightarrow }\mathscr{A}\times _{S}\mathscr{A}\stackrel{m}{\rightarrow }\mathscr{A}$
.◻
$\mathscr{A}\times _{S}\mathscr{A}\stackrel{\unicode[STIX]{x1D70E}}{\rightarrow }\mathscr{A}\times _{S}\mathscr{A}\stackrel{m}{\rightarrow }\mathscr{A}$
.◻
Now we assume that
![]() $\mathscr{A}$
is a Beilinson
$\mathscr{A}$
is a Beilinson
![]() $1$
-motive and is good when regarded as an algebraic stack. Let
$1$
-motive and is good when regarded as an algebraic stack. Let
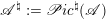 $\mathscr{A}^{\natural }:=\mathscr{P}ic^{\natural }(\mathscr{A})$
be the Picard stack of multiplicative invertible sheaves on
$\mathscr{A}^{\natural }:=\mathscr{P}ic^{\natural }(\mathscr{A})$
be the Picard stack of multiplicative invertible sheaves on
![]() $\mathscr{A}$
with a connection (cf. [Reference LaumonLau96]), and let
$\mathscr{A}$
with a connection (cf. [Reference LaumonLau96]), and let
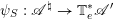 $\unicode[STIX]{x1D713}_{S}:\mathscr{A}^{\natural }\rightarrow \mathbb{T}_{e}^{\ast }\mathscr{A}^{\prime }$
be the
$\unicode[STIX]{x1D713}_{S}:\mathscr{A}^{\natural }\rightarrow \mathbb{T}_{e}^{\ast }\mathscr{A}^{\prime }$
be the
![]() $p$
-curvature morphism as given in Proposition B.3.4(1). By [Reference Ogus and VologodskyOV07, §4.3], there is a natural action of
$p$
-curvature morphism as given in Proposition B.3.4(1). By [Reference Ogus and VologodskyOV07, §4.3], there is a natural action of
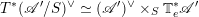 $T^{\ast }(\mathscr{A}^{\prime }/S)^{\vee }\simeq (\mathscr{A}^{\prime })^{\vee }\times _{S}\mathbb{T}_{e}^{\ast }\mathscr{A}^{\prime }$
on
$T^{\ast }(\mathscr{A}^{\prime }/S)^{\vee }\simeq (\mathscr{A}^{\prime })^{\vee }\times _{S}\mathbb{T}_{e}^{\ast }\mathscr{A}^{\prime }$
on
![]() $\mathscr{A}^{\natural }$
. Concretely, for any
$\mathscr{A}^{\natural }$
. Concretely, for any
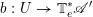 $b:U\rightarrow \mathbb{T}_{e}^{\ast }\mathscr{A}^{\prime }$
objects in
$b:U\rightarrow \mathbb{T}_{e}^{\ast }\mathscr{A}^{\prime }$
objects in
 $\mathscr{A}^{\natural }\times _{\mathbb{T}_{e}^{\ast }\mathscr{A}^{\prime }}U$
consist of multiplicative line bundles on
$\mathscr{A}^{\natural }\times _{\mathbb{T}_{e}^{\ast }\mathscr{A}^{\prime }}U$
consist of multiplicative line bundles on
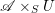 $\mathscr{A}\times _{S}U$
with a connection whose
$\mathscr{A}\times _{S}U$
with a connection whose
![]() $p$
-curvature is equal to
$p$
-curvature is equal to
![]() $b$
. Then for any
$b$
. Then for any
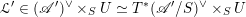 ${\mathcal{L}}^{\prime }\in (\mathscr{A}^{\prime })^{\vee }\times _{S}U\simeq T^{\ast }(\mathscr{A}^{\prime }/S)^{\vee }\times _{S}U$
and
${\mathcal{L}}^{\prime }\in (\mathscr{A}^{\prime })^{\vee }\times _{S}U\simeq T^{\ast }(\mathscr{A}^{\prime }/S)^{\vee }\times _{S}U$
and
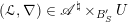 $({\mathcal{L}},\unicode[STIX]{x1D6FB})\in \mathscr{A}^{\natural }\times _{B_{S}^{\prime }}U$
we define
$({\mathcal{L}},\unicode[STIX]{x1D6FB})\in \mathscr{A}^{\natural }\times _{B_{S}^{\prime }}U$
we define
 $$\begin{eqnarray}{\mathcal{L}}^{\prime }\cdot ({\mathcal{L}},\unicode[STIX]{x1D6FB}):=(F_{\mathscr{ A}}^{\ast }{\mathcal{L}}^{\prime }\otimes {\mathcal{L}},\unicode[STIX]{x1D6FB}_{F_{\mathscr{A}}^{\ast }{\mathcal{L}}^{\prime }}\otimes \unicode[STIX]{x1D6FB}),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}^{\prime }\cdot ({\mathcal{L}},\unicode[STIX]{x1D6FB}):=(F_{\mathscr{ A}}^{\ast }{\mathcal{L}}^{\prime }\otimes {\mathcal{L}},\unicode[STIX]{x1D6FB}_{F_{\mathscr{A}}^{\ast }{\mathcal{L}}^{\prime }}\otimes \unicode[STIX]{x1D6FB}),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FB}_{F_{\mathscr{A}}^{\ast }{\mathcal{L}}^{\prime }}$
is the canonical connection on
$\unicode[STIX]{x1D6FB}_{F_{\mathscr{A}}^{\ast }{\mathcal{L}}^{\prime }}$
is the canonical connection on
![]() $F_{\mathscr{A}}^{\ast }{\mathcal{L}}^{\prime }$
giving by the Cartier descent. It also follows from the Cartier descent that
$F_{\mathscr{A}}^{\ast }{\mathcal{L}}^{\prime }$
giving by the Cartier descent. It also follows from the Cartier descent that
![]() $\mathscr{A}^{\natural }$
is a
$\mathscr{A}^{\natural }$
is a
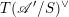 $T(\mathscr{A}^{\prime }/S)^{\vee }$
-torsor under this action.
$T(\mathscr{A}^{\prime }/S)^{\vee }$
-torsor under this action.
On the other hand, recall that for a
![]() $\mathbb{G}_{m}$
-gerbe
$\mathbb{G}_{m}$
-gerbe
![]() $\mathscr{D}$
with commutative group structure on a Beilinson
$\mathscr{D}$
with commutative group structure on a Beilinson
![]() $1$
-motive
$1$
-motive
![]() $\mathscr{P}$
, we defined the
$\mathscr{P}$
, we defined the
![]() $\mathscr{P}^{\vee }$
-torsor
$\mathscr{P}^{\vee }$
-torsor
![]() $\mathscr{T}_{\mathscr{D}}$
of multiplicative splittings of
$\mathscr{T}_{\mathscr{D}}$
of multiplicative splittings of
![]() $\mathscr{D}$
(cf. §A.7).
$\mathscr{D}$
(cf. §A.7).
Proposition C.1.2. There is a canonical
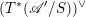 $(T^{\ast }(\mathscr{A}^{\prime }/S))^{\vee }$
-equivariant isomorphism
$(T^{\ast }(\mathscr{A}^{\prime }/S))^{\vee }$
-equivariant isomorphism
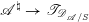 $\mathscr{A}^{\natural }\rightarrow \mathscr{T}_{\mathscr{D}_{\mathscr{A}/S}}$
.
$\mathscr{A}^{\natural }\rightarrow \mathscr{T}_{\mathscr{D}_{\mathscr{A}/S}}$
.
Proof. We sketch the proof. Write
![]() $\mathscr{T}_{\mathscr{D}_{\mathscr{A}/S}}$
by
$\mathscr{T}_{\mathscr{D}_{\mathscr{A}/S}}$
by
![]() $\mathscr{T}_{\mathscr{D}}$
for simplicity. Recall that for
$\mathscr{T}_{\mathscr{D}}$
for simplicity. Recall that for
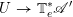 $U\rightarrow \mathbb{T}_{e}^{\ast }\mathscr{A}^{\prime }$
,
$U\rightarrow \mathbb{T}_{e}^{\ast }\mathscr{A}^{\prime }$
,
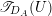 $\mathscr{T}_{D_{A}}(U)$
is the groupoid of splittings of
$\mathscr{T}_{D_{A}}(U)$
is the groupoid of splittings of
![]() $\mathscr{D}_{\mathscr{A}/S}$
over
$\mathscr{D}_{\mathscr{A}/S}$
over
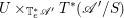 $U\times _{\mathbb{T}_{e}^{\ast }\mathscr{A}^{\prime }}T^{\ast }(\mathscr{A}^{\prime }/S)$
which are compatible with the commutative group structure of
$U\times _{\mathbb{T}_{e}^{\ast }\mathscr{A}^{\prime }}T^{\ast }(\mathscr{A}^{\prime }/S)$
which are compatible with the commutative group structure of
![]() $\mathscr{D}_{\mathscr{A}/S}$
. Note that
$\mathscr{D}_{\mathscr{A}/S}$
. Note that
 $$\begin{eqnarray}U\times _{\mathbb{T}_{e}^{\ast }\mathscr{A}^{\prime }}T^{\ast }(\mathscr{A}^{\prime }/S)\simeq U\times _{\mathbb{ T}_{e}^{\ast }\mathscr{A}^{\prime }}(\mathbb{T}_{e}^{\ast }\mathscr{A}^{\prime }\times _{S}\mathscr{A}^{\prime })\simeq \mathscr{A}^{\prime }\times _{S}U,\end{eqnarray}$$
$$\begin{eqnarray}U\times _{\mathbb{T}_{e}^{\ast }\mathscr{A}^{\prime }}T^{\ast }(\mathscr{A}^{\prime }/S)\simeq U\times _{\mathbb{ T}_{e}^{\ast }\mathscr{A}^{\prime }}(\mathbb{T}_{e}^{\ast }\mathscr{A}^{\prime }\times _{S}\mathscr{A}^{\prime })\simeq \mathscr{A}^{\prime }\times _{S}U,\end{eqnarray}$$
and under this isomorphism, the projection of left-hand side to the second factor is identified with
 $$\begin{eqnarray}\mathscr{A}^{\prime }\times _{S}U\rightarrow \mathscr{A}^{\prime }\times _{S}\mathscr{A}^{\natural }\rightarrow T^{\ast }(\mathscr{A}^{\prime }/S).\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{A}^{\prime }\times _{S}U\rightarrow \mathscr{A}^{\prime }\times _{S}\mathscr{A}^{\natural }\rightarrow T^{\ast }(\mathscr{A}^{\prime }/S).\end{eqnarray}$$
Now by Lemma B.3.4, the pullback of
![]() $\mathscr{D}_{\mathscr{A}/S}$
to
$\mathscr{D}_{\mathscr{A}/S}$
to
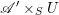 $\mathscr{A}^{\prime }\times _{S}U$
has a canonical splitting
$\mathscr{A}^{\prime }\times _{S}U$
has a canonical splitting
![]() ${\mathcal{L}}_{U,\unicode[STIX]{x1D6FC}}$
. Moreover, one can check that this canonical splitting is compatible with the commutative group structure of
${\mathcal{L}}_{U,\unicode[STIX]{x1D6FC}}$
. Moreover, one can check that this canonical splitting is compatible with the commutative group structure of
![]() $\mathscr{D}_{\mathscr{A}/S}$
. Thus the assignment
$\mathscr{D}_{\mathscr{A}/S}$
. Thus the assignment
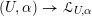 $(U,\unicode[STIX]{x1D6FC})\rightarrow {\mathcal{L}}_{U,\unicode[STIX]{x1D6FC}}$
defines a map from
$(U,\unicode[STIX]{x1D6FC})\rightarrow {\mathcal{L}}_{U,\unicode[STIX]{x1D6FC}}$
defines a map from
![]() $\mathscr{A}^{\natural }$
to
$\mathscr{A}^{\natural }$
to
![]() $\mathscr{T}_{\mathscr{D}}$
which is compatible with their
$\mathscr{T}_{\mathscr{D}}$
which is compatible with their
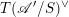 $T(\mathscr{A}^{\prime }/S)^{\vee }$
-torsor structures hence an equivalence.◻
$T(\mathscr{A}^{\prime }/S)^{\vee }$
-torsor structures hence an equivalence.◻
As a corollary, we obtain the following theorem.
Theorem C.1.3. Let
![]() $\mathscr{A}$
be a good Beilinson
$\mathscr{A}$
be a good Beilinson
![]() $1$
-motive. Then there is a canonical equivalence of categories
$1$
-motive. Then there is a canonical equivalence of categories
 $$\begin{eqnarray}D^{b}({\mathcal{D}}\text{-}\text{mod}(\mathscr{A}))\simeq D^{b}(\operatorname{QCoh}(\mathscr{A}^{\natural })).\end{eqnarray}$$
$$\begin{eqnarray}D^{b}({\mathcal{D}}\text{-}\text{mod}(\mathscr{A}))\simeq D^{b}(\operatorname{QCoh}(\mathscr{A}^{\natural })).\end{eqnarray}$$
Remark C.1.4. Note that in [Reference LaumonLau96], this theorem is proved for abelian schemes over
![]() $S$
of characteristic zero. In fact, Laumon’s construction applies to any ‘good’ Beilinson
$S$
of characteristic zero. In fact, Laumon’s construction applies to any ‘good’ Beilinson
![]() $1$
-motive over a locally Noetherian base. When
$1$
-motive over a locally Noetherian base. When
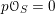 $p{\mathcal{O}}_{S}=0$
, it is easy to see that Laumon’s equivalence and the equivalence constructed above are the same.
$p{\mathcal{O}}_{S}=0$
, it is easy to see that Laumon’s equivalence and the equivalence constructed above are the same.
In particular, let
 $\unicode[STIX]{x1D703}:\mathscr{A}^{\prime }\rightarrow \mathbb{T}^{\ast }\mathscr{A}^{\prime }$
be a section obtained by base change
$\unicode[STIX]{x1D703}:\mathscr{A}^{\prime }\rightarrow \mathbb{T}^{\ast }\mathscr{A}^{\prime }$
be a section obtained by base change
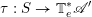 $\unicode[STIX]{x1D70F}:S\rightarrow \mathbb{T}_{e}^{\ast }\mathscr{A}^{\prime }$
. Let
$\unicode[STIX]{x1D70F}:S\rightarrow \mathbb{T}_{e}^{\ast }\mathscr{A}^{\prime }$
. Let
 $\mathscr{D}_{\mathscr{A}/S}(\unicode[STIX]{x1D703}):=\unicode[STIX]{x1D703}^{\ast }\mathscr{D}_{\mathscr{A}/S}$
. Then
$\mathscr{D}_{\mathscr{A}/S}(\unicode[STIX]{x1D703}):=\unicode[STIX]{x1D703}^{\ast }\mathscr{D}_{\mathscr{A}/S}$
. Then
![]() $\mathscr{D}_{\mathscr{A}/S,\unicode[STIX]{x1D703}}$
is a
$\mathscr{D}_{\mathscr{A}/S,\unicode[STIX]{x1D703}}$
is a
![]() $\mathbb{G}_{m}$
-gerbe on
$\mathbb{G}_{m}$
-gerbe on
![]() $\mathscr{A}^{\prime }$
equipped with a canonical commutative group structure, and the
$\mathscr{A}^{\prime }$
equipped with a canonical commutative group structure, and the
![]() ${\mathscr{A}^{\prime }}^{\vee }$
-torsor
${\mathscr{A}^{\prime }}^{\vee }$
-torsor
![]() $\mathscr{T}_{\mathscr{D}_{\mathscr{A}/S,\unicode[STIX]{x1D703}}}$
of multiplicative splittings can be identified with
$\mathscr{T}_{\mathscr{D}_{\mathscr{A}/S,\unicode[STIX]{x1D703}}}$
of multiplicative splittings can be identified with
 $\mathscr{A}^{\natural }\times _{\mathbb{T}_{e}^{\ast }\mathscr{A}^{\prime },\unicode[STIX]{x1D70F}}S$
.
$\mathscr{A}^{\natural }\times _{\mathbb{T}_{e}^{\ast }\mathscr{A}^{\prime },\unicode[STIX]{x1D70F}}S$
.
C.2 A variant
In the main body of the paper, however, we need a variant of the above construction. Let
![]() $k$
be an algebraically closed field of characteristic
$k$
be an algebraically closed field of characteristic
![]() $p$
. For a
$p$
. For a
![]() $k$
-scheme
$k$
-scheme
![]() $X$
, we denote by
$X$
, we denote by
![]() $X^{\prime }$
its Frobenius base change along
$X^{\prime }$
its Frobenius base change along
 $Fr:k\rightarrow k$
. Let
$Fr:k\rightarrow k$
. Let
![]() $S$
be a smooth
$S$
be a smooth
![]() $k$
-scheme. For an
$k$
-scheme. For an
![]() $S$
-scheme
$S$
-scheme
![]() $X\rightarrow S$
, we denote by
$X\rightarrow S$
, we denote by
![]() $X^{(S)}$
its base change along
$X^{(S)}$
its base change along
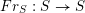 $Fr_{S}:S\rightarrow S$
. Let
$Fr_{S}:S\rightarrow S$
. Let
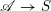 $\mathscr{A}\rightarrow S$
be a Picard stack with multiplication
$\mathscr{A}\rightarrow S$
be a Picard stack with multiplication
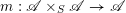 $m:\mathscr{A}\times _{S}\mathscr{A}\rightarrow \mathscr{A}$
. The goal of this subsection is to construct certain multiplicative gerbe
$m:\mathscr{A}\times _{S}\mathscr{A}\rightarrow \mathscr{A}$
. The goal of this subsection is to construct certain multiplicative gerbe
![]() $\mathscr{D}_{\mathscr{A}}(\unicode[STIX]{x1D703})$
on
$\mathscr{D}_{\mathscr{A}}(\unicode[STIX]{x1D703})$
on
![]() $\mathscr{A}^{\prime }$
(rather than on
$\mathscr{A}^{\prime }$
(rather than on
![]() $\mathscr{A}^{(S)}$
as done at the end of the previous subsection).
$\mathscr{A}^{(S)}$
as done at the end of the previous subsection).
Let
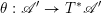 $\unicode[STIX]{x1D703}:\mathscr{A}^{\prime }\rightarrow T^{\ast }\mathscr{A}^{\prime }$
be a section, where
$\unicode[STIX]{x1D703}:\mathscr{A}^{\prime }\rightarrow T^{\ast }\mathscr{A}^{\prime }$
be a section, where
![]() $T^{\ast }\mathscr{A}^{\prime }$
is the cotangent bundle of
$T^{\ast }\mathscr{A}^{\prime }$
is the cotangent bundle of
![]() $\mathscr{A}^{\prime }$
relative to
$\mathscr{A}^{\prime }$
relative to
![]() $k$
. We say
$k$
. We say
![]() $\unicode[STIX]{x1D703}$
is multiplicative if the upper right corner of the following diagram is commutative.
$\unicode[STIX]{x1D703}$
is multiplicative if the upper right corner of the following diagram is commutative.

Let
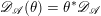 $\mathscr{D}_{\mathscr{A}}(\unicode[STIX]{x1D703})=\unicode[STIX]{x1D703}^{\ast }\mathscr{D}_{\mathscr{A}}$
be the pullback of
$\mathscr{D}_{\mathscr{A}}(\unicode[STIX]{x1D703})=\unicode[STIX]{x1D703}^{\ast }\mathscr{D}_{\mathscr{A}}$
be the pullback of
![]() $\mathscr{D}_{\mathscr{A}}$
to
$\mathscr{D}_{\mathscr{A}}$
to
![]() $\mathscr{A}^{\prime }$
. Then by the same argument as in Lemma C.1.1, we have the following.
$\mathscr{A}^{\prime }$
. Then by the same argument as in Lemma C.1.1, we have the following.
Lemma C.2.1 (See also [Reference Bezrukavnikov and BravermanBB07, Lemma 3.16]).
Let
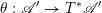 $\unicode[STIX]{x1D703}:\mathscr{A}^{\prime }\rightarrow T^{\ast }\mathscr{A}^{\prime }$
be a multiplicative section. Then
$\unicode[STIX]{x1D703}:\mathscr{A}^{\prime }\rightarrow T^{\ast }\mathscr{A}^{\prime }$
be a multiplicative section. Then
![]() $\mathscr{D}_{\mathscr{A}}(\unicode[STIX]{x1D703})$
is a
$\mathscr{D}_{\mathscr{A}}(\unicode[STIX]{x1D703})$
is a
![]() $\mathbb{G}_{m}$
-gerbe on
$\mathbb{G}_{m}$
-gerbe on
![]() $\mathscr{A}^{\prime }$
with a commutative group structure.
$\mathscr{A}^{\prime }$
with a commutative group structure.