Hostname: page-component-848d4c4894-v5vhk Total loading time: 0 Render date: 2024-06-28T01:47:24.489Z Has data issue: false hasContentIssue false
  • English
  • Français

Automorphisms of surfaces of general type with 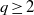$q\geq 2$ acting trivially in cohomology

Part of: Surfaces and higher-dimensional varieties

Published online by Cambridge University Press:  07 August 2013

Jin-Xing Cai ,
Wenfei Liu  and
Lei Zhang
Jin-Xing Cai
Affiliation:
LMAM, School of Mathematical Sciences, Peking University, Beijing 100871, PR China email jxcai@math.pku.edu.cn
Wenfei Liu
Affiliation:
Fakultät für Mathematik, Universtät Bielefeld, Universitätsstr. 25, 33615 Bielefeld, Germany email liuwenfei@math.uni-bielefeld.de
Lei Zhang
Affiliation:
College of Mathematics and Information Sciences, Shaanxi Normal University, Xi’an 710062, PR China email lzhpkutju@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we prove that surfaces of general type with irregularity 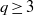$q\geq 3$ are rationally cohomologically rigidified, and so are minimal surfaces 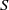$S$ with 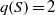$q(S)= 2$ unless 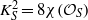${ K}_{S}^{2} = 8\chi ({ \mathcal{O} }_{S} )$. Here a surface 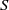$S$ is said to be rationally cohomologically rigidified if its automorphism group 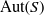$\mathrm{Aut} (S)$ acts faithfully on the cohomology ring 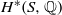${H}^{\ast } (S, \mathbb{Q} )$. As examples we give a complete classification of surfaces isogenous to a product with 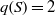$q(S)= 2$ that are not rationally cohomologically rigidified.

Keywords

surface of general typevariety of maximal Albanese dimensionautomorphismcohomology

MSC classification

Secondary: 14J50: Automorphisms of surfaces and higher-dimensional varieties 14J29: Surfaces of general type
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 10 , October 2013 , pp. 1667 - 1684
Copyright
© The Author(s) 2013 

References

Atiyah, M. and Singer, I. M., The index of elliptic operators III, Ann. of Math. (2) 87 (1968), 546–604.Google Scholar
Barja, M. A., Lahoz, M., Naranjo, J. C. and Pareschi, G., On the bicanonical map of irregular varieties, J. Algebraic Geom. 21 (2012), 445–471.Google Scholar
Barth, W. P., Hulek, K., Peters, C. A. M. and Van de Ven, A., Compact complex surfaces, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. 4, 2nd edition (Springer, Berlin, 2004).Google Scholar
Bauer, I. C. and Catanese, F., Inoue type manifolds and Inoue surfaces: a connected component of the moduli space of surfaces with ${K}^{2} = 7$, ${p}_{g} = 0$, in Geometry and arithmetic, EMS Series of Congress Reports (European Mathematical Society, Zürich, 2012), 23–56.Google Scholar
Beauville, A., L’inégalité ${p}_{g} \geq 2q- 4$ pour les surfaces de type général, Appendice à O. Debarre: ‘Inégalités numériques pour les surfaces de type général, Bull. Soc. Math. France 110 (1982), 343–346.Google Scholar
Beauville, A., Variétés Kähleriennes dont la première classe de Chern est nulle, J. Differential Geom. 18 (1984), 755–782.Google Scholar
Beauville, A., Annulation du ${H}^{1} $ pour les fibrés en droites plats, Complex algebraic varieties, in Proc. Conf., Bayreuth, 1990, Springer Lecture Notes in Mathematics, vol. 1507 (Springer, 1992), 1–15.Google Scholar
Boissière, S., Nieper-Wisskirchen, M and Sarti, A., Higher dimensional Enriques varieties and automorphisms of generalized Kummer varieties, J. Math. Pures Appl. (9) 95 (2011), 553–563.CrossRefGoogle Scholar
Borel, A. and Narasimhan, R., Uniqueness conditions for certain holomorphic mappings, Invent. Math. 2 (1967), 247–255.CrossRefGoogle Scholar
Broughton, S. A., The homology and higher representations of the automorphism group of a Riemann surface, Trans. Amer. Math. Soc. 300 (1987), 153–158.Google Scholar
Burns, D. and Rapoport, M., On the Torelli problem for Kählerian K3 surfaces, Ann. Sci. École Norm. Super. 4 (1975), 235–274.Google Scholar
Cai, J.-X., Automorphisms of a surface of general type acting trivially in cohomology, Tohoku Math. J. 56 (2004), 341–355.Google Scholar
Cai, J.-X., Automorphisms of fiber surfaces of genus 2, inducing the identity in cohomology, Trans. Amer. Math. Soc. 358 (2006), 1187–1201.Google Scholar
Cai, J.-X., Classification of fiber surfaces of genus 2 with automorphisms acting trivially in cohomology, Pacific J. Math. 232 (2007), 43–59.Google Scholar
Cai, J.-X., Automorphisms of an irregular surface with low slope acting trivially in cohomology, Algebraic geometry in East Asia: Seoul 2008, Advanced Studies in Pure Mathematics, vol. 60 (Mathematical Society of Japan, 2010), 183–194.Google Scholar
Cai, J.-X., Automorphisms of an irregular surface of general type acting trivially in cohomology, II, Tohoku Math. J. 64 (2012), 593–605.Google Scholar
Catanese, F., Moduli and classification of irregular Kaehler manifolds (and algebraic varieties) with Albanese general type fibrations, Invent. Math. 104 (1991), 389–407.Google Scholar
Catanese, F., Fibred surfaces, varieties isogenous to a product and related moduli spaces, Amer. J. Math. 122 (2000), 1–44.Google Scholar
Catanese, F., Moduli spaces of surfaces and real structures, Ann. of Math. (2) 158 (2003), 577–592.Google Scholar
Catanese, F., A superficial working guide to deformations and moduli, in Handbook of Moduli, Vol. I, Advanced Lectures in Mathematics, vol. 24, eds Farkas, G. and Morrison, I. (International Press, 2012), 161–216.Google Scholar
Green, M. and Lazarsfeld, R., Deformation theory, Generic vanishing theorems and some conjectures of Enriques, Catanese and Beauville, Invent. Math. 90 (1987), 389–407.Google Scholar
Green, M. and Lazarsfeld, R., Higher obstruction to deformation of cohomology of line bundles, J. Amer. Math. Soc. 4 (1991), 87–103.Google Scholar
Hacon, C. D., A derived approach to generic vanishing, J. Rein. Angew. Math. 575 (2004), 173–187.Google Scholar
Isaacs, I. M., Character theory of finite groups (Academic Press, 1976).Google Scholar
Liu, W., Surfaces isogenous to a product: their automorphisms and degenerations, PhD thesis, Bayreuth University (2010).Google Scholar
Mukai, S., Numerically trivial involutions of Kummer type of an Enriques surface, Kyoto J. Math. 50 (2010), 889–902.CrossRefGoogle Scholar
Mukai, S. and Namikawa, Y., Automorphisms of Enriques surfaces which act trivially on the cohomology groups, Invent. Math. 77 (1984), 383–397.Google Scholar
Oguiso, K., No cohomologically trivial non-trivial automorphism of generalized Kummer manifolds, Preprint (2012), arXiv:1208.3750.Google Scholar
Pardini, R., The Severi inequality ${K}^{2} \geq 4\chi $ for surfaces with maximal Albanese dimension, Invent. Math. 159 (2005), 669–672.Google Scholar
Pareschi, G. and Popa, M., Regularity on abelian varieties, I, J. Amer. Math. Soc. 16 (2003), 285–302.CrossRefGoogle Scholar
Pareschi, G. and Popa, M., Regularity on abelian varieties III: relationship with Generic Vanishing and applications, Clay. Math. Proc. (2006), 141–168.Google Scholar
Pareschi, G. and Popa, M., Strong generic vanishing and Higher-dimensional Castelnuovo–de Franchis inequality, Duke J. Math. 150 (2009), 269–285.Google Scholar
Peters, C. A. M., Holomorphic automorphisms of compact Kähler surfaces and their induced actions in cohomology, Invent. Math. 52 (1979), 143–148.CrossRefGoogle Scholar
Peters, C. A. M., On automorphisms of compact Kähler surfaces, in Algebraic geometry angers 1979 (Alphen aan de Rijn, Sijthoff and Noordhoff, 1980).Google Scholar
Popp, H., Moduli theory and classification theory of algebraic varieties, Lecture Notes in Mathematics, vol. 620 (Springer, Berlin–New York, 1977).Google Scholar
Tirabassi, S., Syzygies, pluricanonical maps and the birational geometry of irregular varieties, Thesis submitted to Università degli studi Roma Tre (2011).Google Scholar
Xiao, G., L’irrégularité des surfaces de type général dont le système canonique est composé d’un pinceau, Compositio Math. 56 (1985), 251–257.Google Scholar
Xiao, G., Bound of automorphisms of surfaces of general type, I, Ann. of Math. (2) 139 (1994), 51–77.Google Scholar