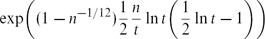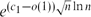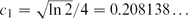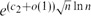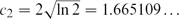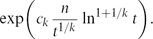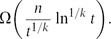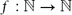Paper
On the Spread of Random Graphs
-
- Published online by Cambridge University Press:
- 13 June 2014, pp. 477-504
-
- Article
- Export citation
Bounded-Size Rules: The Barely Subcritical Regime
-
- Published online by Cambridge University Press:
- 28 May 2014, pp. 505-538
-
- Article
- Export citation
Counting Independent Sets in Hypergraphs
-
- Published online by Cambridge University Press:
- 08 April 2014, pp. 539-550
-
- Article
- Export citation
Colouring Planar Graphs With Three Colours and No Large Monochromatic Components
-
- Published online by Cambridge University Press:
- 01 April 2014, pp. 551-570
-
- Article
- Export citation
New Bounds for Edge-Cover by Random Walk
-
- Published online by Cambridge University Press:
- 11 March 2014, pp. 571-584
-
- Article
- Export citation
Intersection Conductance and Canonical Alternating Paths: Methods for General Finite Markov Chains
-
- Published online by Cambridge University Press:
- 13 June 2014, pp. 585-606
-
- Article
- Export citation
Cycles Are Strongly Ramsey-Unsaturated
-
- Published online by Cambridge University Press:
- 29 April 2014, pp. 607-630
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
CPC volume 23 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 13 June 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
CPC volume 23 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 13 June 2014, pp. b1-b8
-
- Article
-
- You have access
- Export citation