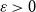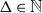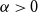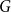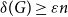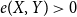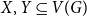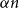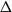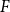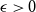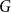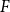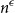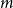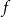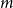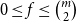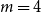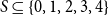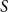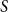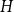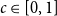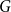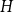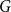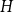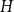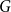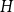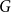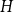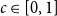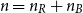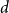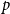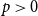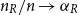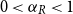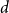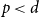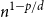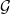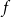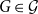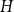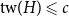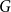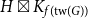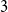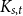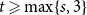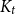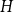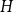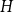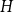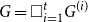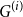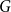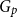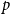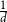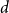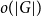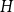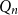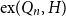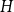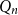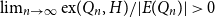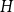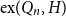We consider bond percolation on high-dimensional product graphs 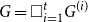 $G=\square _{i=1}^tG^{(i)}$, where
$G=\square _{i=1}^tG^{(i)}$, where  $\square$ denotes the Cartesian product. We call the
$\square$ denotes the Cartesian product. We call the 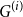 $G^{(i)}$ the base graphs and the product graph
$G^{(i)}$ the base graphs and the product graph 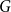 $G$ the host graph. Very recently, Lichev (J. Graph Theory, 99(4):651–670, 2022) showed that, under a mild requirement on the isoperimetric properties of the base graphs, the component structure of the percolated graph
$G$ the host graph. Very recently, Lichev (J. Graph Theory, 99(4):651–670, 2022) showed that, under a mild requirement on the isoperimetric properties of the base graphs, the component structure of the percolated graph 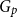 $G_p$ undergoes a phase transition when
$G_p$ undergoes a phase transition when 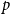 $p$ is around
$p$ is around 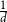 $\frac{1}{d}$, where
$\frac{1}{d}$, where 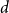 $d$ is the average degree of the host graph.
$d$ is the average degree of the host graph.
In the supercritical regime, we strengthen Lichev’s result by showing that the giant component is in fact unique, with all other components of order 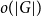 $o(|G|)$, and determining the sharp asymptotic order of the giant. Furthermore, we answer two questions posed by Lichev (J. Graph Theory, 99(4):651–670, 2022): firstly, we provide a construction showing that the requirement of bounded degree is necessary for the likely emergence of a linear order component; secondly, we show that the isoperimetric requirement on the base graphs can be, in fact, super-exponentially small in the dimension. Finally, in the subcritical regime, we give an example showing that in the case of irregular high-dimensional product graphs, there can be a polynomially large component with high probability, very much unlike the quantitative behaviour seen in the Erdős-Rényi random graph and in the percolated hypercube, and in fact in any regular high-dimensional product graphs, as shown by the authors in a companion paper (Percolation on high-dimensional product graphs. arXiv:2209.03722, 2022).
$o(|G|)$, and determining the sharp asymptotic order of the giant. Furthermore, we answer two questions posed by Lichev (J. Graph Theory, 99(4):651–670, 2022): firstly, we provide a construction showing that the requirement of bounded degree is necessary for the likely emergence of a linear order component; secondly, we show that the isoperimetric requirement on the base graphs can be, in fact, super-exponentially small in the dimension. Finally, in the subcritical regime, we give an example showing that in the case of irregular high-dimensional product graphs, there can be a polynomially large component with high probability, very much unlike the quantitative behaviour seen in the Erdős-Rényi random graph and in the percolated hypercube, and in fact in any regular high-dimensional product graphs, as shown by the authors in a companion paper (Percolation on high-dimensional product graphs. arXiv:2209.03722, 2022).