Bounded-size rules (BSRs) are dynamic random graph processes which incorporate limited choice along with randomness in the evolution of the system. Typically one starts with the empty graph and at each stage two edges are chosen uniformly at random. One of the two edges is then placed into the system according to a decision rule based on the sizes of the components containing the four vertices. For bounded-size rules, all components of size greater than some fixed K ≥ 1 are accorded the same treatment. Writing BSR(t) for the state of the system with ⌊nt/2⌋ edges, Spencer and Wormald [26] proved that for such rules, there exists a (rule-dependent) critical time tc such that when t < tc the size of the largest component is of order log n, while for t > tc, the size of the largest component is of order n. In this work we obtain upper bounds (that hold with high probability) of order n2γ log4n, on the size of the largest component, at time instants tn = tc−n−γ, where γ ∈ (0,1/4). This result for the barely subcritical regime forms a key ingredient in the study undertaken in [4], of the asymptotic dynamic behaviour of the process describing the vector of component sizes and associated complexity of the components for such random graph models in the critical scaling window. The proof uses a coupling of BSR processes with a certain family of inhomogeneous random graphs with vertices in the type space 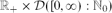$\mathbb{R}_+\times \mathcal{D}([0,\infty):\mathbb{N}_0)$, where 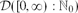$\mathcal{D}([0,\infty):\mathbb{N}_0)$ is the Skorokhod D-space of functions that are right continuous and have left limits, with values in the space of non-negative integers 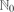$\mathbb{N}_0$, equipped with the usual Skorokhod topology. The coupling construction also gives an alternative characterization (from the usual explosion time of the susceptibility function) of the critical time tc for the emergence of the giant component in terms of the operator norm of integral operators on certain L2 spaces.