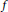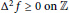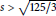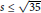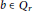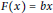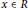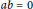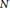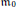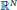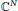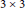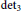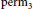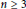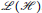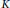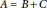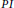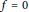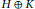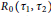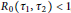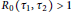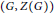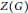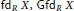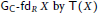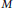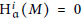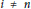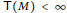Research Article
Convex Functions on Discrete Time Domains
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 225-233
-
- Article
-
- You have access
- Export citation
Award Winners
Research Article
Non-discrete Frieze Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 234-243
-
- Article
-
- You have access
- Export citation
Research Article
A Note on Quaternionic Hyperbolic Ideal Triangle Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 244-257
-
- Article
-
- You have access
- Export citation
Annihilators and Power Values of Generalized Skew Derivations on Lie Ideals
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 258-270
-
- Article
-
- You have access
- Export citation
Artinianness of Composed Graded Local Cohomology Modules
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 271-278
-
- Article
-
- You have access
- Export citation
The Poincaré–Deligne Polynomial of Milnor Fibers of Triple Point Line Arrangements is Combinatorially Determined
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 279-286
-
- Article
-
- You have access
- Export citation
An Existence Theory for Incomplete Designs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 287-302
-
- Article
-
- You have access
- Export citation
Non-extendable Zero Sets of Harmonic and Holomorphic Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 303-310
-
- Article
-
- You have access
- Export citation
Product Ranks of the 3 × 3 Determinant and Permanent
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 311-319
-
- Article
-
- You have access
- Export citation
Perturbations of Von Neumann Subalgebras With Finite Index
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 320-325
-
- Article
-
- You have access
- Export citation
On the Uniqueness of Jordan Canonical Form Decompositions of Operators by K-theoretical Data
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 326-339
-
- Article
-
- You have access
- Export citation
A Note on Algebras that are Sums of Two Subalgebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 340-345
-
- Article
-
- You have access
- Export citation
On a Theorem of Bers, with Applications to the Study of Automorphism Groups of Domains
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 346-353
-
- Article
-
- You have access
- Export citation
Factoring a Quadratic Operator as a Product of Two Positive Contractions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 354-362
-
- Article
-
- You have access
- Export citation
Dynamical Analysis of a Stage-Structured Model for Lyme Disease with Two Delays
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 363-380
-
- Article
-
- You have access
- Export citation
Supports of Extremal Doubly Stochastic Measures
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 381-391
-
- Article
-
- You have access
- Export citation
Total Character of a Group G with (G, Z(G)) as a Generalized Camina Pair
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 392-402
-
- Article
-
- You have access
- Export citation
On Flat and Gorenstein Flat Dimensions of Local Cohomology Modules
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 403-416
-
- Article
-
- You have access
- Export citation
Existence of Multiple Solutions for a p-Laplacian System in ℝ N with Sign-changing Weight Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 417-434
-
- Article
-
- You have access
- Export citation
On Extensions of Stably Finite C*-Algebras (II)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 435-439
-
- Article
-
- You have access
- Export citation