Hostname: page-component-848d4c4894-v5vhk Total loading time: 0 Render date: 2024-06-28T07:54:06.073Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamical Analysis of a Stage-Structured Model for Lyme Disease with Two Delays

Published online by Cambridge University Press:  20 November 2018

Dan Li  and
Wanbiao Ma
Dan Li
Affiliation:
Department of AppliedMathematics, School ofMathematics and Physics, University of Science and Technology Beijing, Beijing, 100083, P.R. China e-mail: dan___li@163.com
Wanbiao Ma
Affiliation:
Fundamental Department, TianJin College, University of Science and Technology Beijing, Tianjin, 301830, P. R. China e-mail: (Wanbiao Ma, the corresponding author) wanbiao_ma@ustb.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, a nonlinear stage-structured model for Lyme disease is considered. The model is a system of diòerential equations with two time delays. We derive the basic reproductive rate 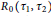${{R}_{0}}\left( {{\tau }_{1}},\,{{\tau }_{2}} \right)$. If 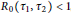${{R}_{0}}\left( {{\tau }_{1}},\,{{\tau }_{2}} \right)\,<\,1$, then the boundary equilibrium is globally asymptotically stable. If ${{R}_{0}}\left( {{\tau }_{1}},\,{{\tau }_{2}} \right)\,>\,1$, then there exists a unique positive equilibrium whose local asymptotic stability and the existence of Hopf bifurcations are established by analyzing the distribution of the characteristic values. An explicit algorithm for determining the direction of Hopf bifurcations and the stability of the bifurcating periodic solutions is derived by using the normal form and the center manifold theory. Some numerical simulations are performed to confirm the correctness of theoretical analysis. Finally, some conclusions are given.

Keywords

34D20diseasestage-structuretime delayLyapunov functional stabilityHopf bifurcation
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 2 , 01 June 2016 , pp. 363 - 380
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Aiello, W. G. and Freedman, H. I., A time delay model of single-species growth with stage structure. Math.Biosci. 101(1990), 139–153. http://dx.doi.org/10.1016/0025-5564(90)90019-U Google Scholar
[2] Aiello, W. G., Freedman, H. I., and Wu, J., Analysis of a model representing stage-structured population growth with state dependent time delay. SIAM J. Appl. Math. 52(1992), no. 3, 855–869. http://dx.doi.org/10.1137/0152048 Google Scholar
[3] Barbour, A. G. and Fish, D., The biological and social phenomenon ofLyme disease. Science 260(1993), 1610–1616.Google Scholar
[4] Beretta, E. and Kuang, Y., Geometric stability switch criteria in delay differential systems with delay dependant parameters. SIAM J. Math. Appl. 33(2002), 1144–1165. http://dx.doi.org/10.1137/S0036141000376086 Google Scholar
[5] Caraco, T., Gardner, G., Maniatty, W., Deelman, E., and Szymanski, B., Lyme disease: self-regulation and pathogen invasion. J. Theor. Biol. 193(1998), 561–575.Google Scholar
[6] Caraco, T., Glavanakov, S., Chen, G., Flaherty, J., Ohsumi, T., and Szymanski, B., Stage-structured infection transmission and a spatial epidemic: A model for Lyme disease. Am. Nat. 160(2002), 348–359.Google Scholar
[7] Guo, H. and Li, M. Y., Global stability in a mathematical model of tuberculosis. Can. Appl. Math. Q. 14(2004), 185–197.Google Scholar
[8] Hale, J. and Lunel, S., Introduction to functional differential equations. Springer-Verlag, New York, 1993.Google Scholar
[9] Hassard, B., Kazarinoff, N., and Wan, Y., Theory and application of Hopf bifurcation. Cambridge: Cambridge University Press, 1981.Google Scholar
[10] Korobeinikov, A. and Maini, K. A., A Lyapunov function and global properties for sir and seir epidemiological models with nonlinear incidence. Math.Biosci. Eng. 1(2004), 57–60. http://dx.doi.org/10.3934/mbe.2004.1.57 Google Scholar
[11] Kurtenbach, K., Hanincova, K., Tsao, J. I., Margos, G., Fish, D., and Ogden, N. H., Fundamental processes in the evolutionary ecology of lymeborreliosis. Nat. Rev. Microbiol. 4(2006), 660–669.Google Scholar
[12] Liu, X. and Zhao, X., A periodic epidemic model with age structure in a patchy environment. SIAM J. Appl. Math. 71(2011), 1896–1917. http://dx.doi.org/10.1137/100813610 Google Scholar
[13] Ma, Z., Liu, J., and Li, J., Stability analysis for differential infectivity epidemic models. Nonlinear Anal. Real World Appl. 4(2003), 841–856. http://dx.doi.org/10.1016/S1468-1218(03)00019-1 Google Scholar
[14] Ruan, S. and Wei, J., On the zeros of a third degree exponential polynomial with applications to a delayed model for the control of testosterone secretion. IMA J. Math. Appl. Med. Biol. 18(2001), 41–52.Google Scholar
[15] Wang, W. and Zhao, X., An age-structured epidemic model in a patchy environment. SIAM J. Appl. Math. 68(2005), 1597–1614. http://dx.doi.org/10.1137/S0036139903431245 Google Scholar
[16] White, D. J., Lyme disease, Oxford University Press. New York. 1998.Google Scholar
[17] Yu, C., Wei, J., and Zou, X., Bifurcation analysis in an age-structured model of a single single species living in two identical patches. Appl. Math. Modelling. 34(2010), no. 4,1068-1077. http://dx.doi.org/10.1016/j.apm.2009.07.018 Google Scholar
[18] Zhang, Y. and Zhao, X., A reaction-diffusion Lyme disease model with seasonality. SIAM J. Appl. Math. 73(2013), 2077–2099. http://dx.doi.org/10.1137/120875454 Google Scholar
[19] Zhao, X., Global dynamics of a reaction and diffusion model for Lyme disease. J. Math. Biol. 65(2012), 787–808. http://dx.doi.org/10.1007/s00285-011-0482-9 Google Scholar