No CrossRef data available.
Article contents
Each Copy of the Real Line in 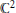 is Removable
is Removable
Published online by Cambridge University Press: 20 November 2018
Abstract
Around 1995, Professors Lupacciolu, Chirka and Stout showed that a closed subset of 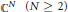 ${{\mathbb{C}}^{N}}\left( N\ge 2 \right)$ is removable for holomorphic functions, if its topological dimension is less than or equal to
${{\mathbb{C}}^{N}}\left( N\ge 2 \right)$ is removable for holomorphic functions, if its topological dimension is less than or equal to 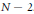 $N\,-\,2$. Besides, they asked whether closed subsets of
$N\,-\,2$. Besides, they asked whether closed subsets of 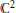 ${{\mathbb{C}}^{2}}$ homeomorphic to the real line (the simplest 1-dimensional sets) are removable for holomorphic functions. In this paper we propose a positive answer to that question.
${{\mathbb{C}}^{2}}$ homeomorphic to the real line (the simplest 1-dimensional sets) are removable for holomorphic functions. In this paper we propose a positive answer to that question.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2001




