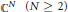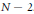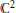Research Article
The Generating Degree of ℂp
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-11
-
- Article
-
- You have access
- Export citation
A Technique of Studying Sums of Central Cantor Sets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 12-18
-
- Article
-
- You have access
- Export citation
Multiplicities of Binary Recurrences
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 19-21
-
- Article
-
- You have access
- Export citation
Gauss Sums of Orders Six and Twelve
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 22-26
-
- Article
-
- You have access
- Export citation
Normal Subloops in the Integral Loop Ring of an RA Loop
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 27-35
-
- Article
-
- You have access
- Export citation
Quantization of Bending Deformations of Polygons In
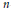 , Hypergeometric Integrals and the Gassner Representation
, Hypergeometric Integrals and the Gassner Representation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 36-60
-
- Article
-
- You have access
- Export citation
The Inequalities for Polynomials and Integration over Fractal Arcs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 61-69
-
- Article
-
- You have access
- Export citation
The Tangent Bundle of an Almost Complex Manifold
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 70-79
-
- Article
-
- You have access
- Export citation
Constructing Compacta of Different Extensional Dimensions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 80-86
-
- Article
-
- You have access
- Export citation
On a New Exponential Sum
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 87-92
-
- Article
-
- You have access
- Export citation
Some Semigroup Laws in Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 93-96
-
- Article
-
- You have access
- Export citation
On the Density of Cyclic Quartic Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 97-104
-
- Article
-
- You have access
- Export citation
Convolution Equation in
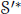 —Propagation of Singularities
—Propagation of Singularities
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 105-114
-
- Article
-
- You have access
- Export citation
Approximation algébrique simultanée de nombres de Liouville
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 115-120
-
- Article
-
- You have access
- Export citation
A Necessary Condition for Multipliers of Weak Type (1, 1)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 121-125
-
- Article
-
- You have access
- Export citation
Each Copy of the Real Line in
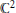 is Removable
is Removable
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 126-128
-
- Article
-
- You have access
- Export citation



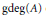
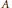
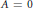
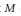
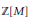
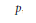
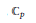
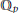
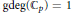

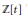
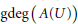
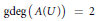
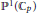
 , Hypergeometric Integrals and the Gassner Representation
, Hypergeometric Integrals and the Gassner Representation
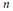
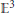
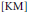
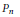
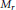
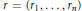
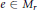

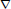
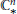
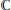
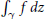
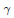
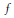
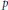
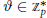

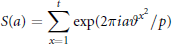


 —Propagation of Singularities
—Propagation of Singularities


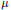
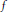
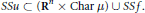
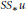
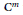

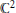 is Removable
is Removable