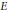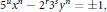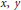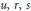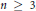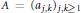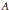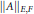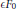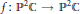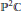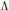Research Article
Heegner Points and the Rank of Elliptic Curves over Large Extensions of Global Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 481-490
-
- Article
-
- You have access
- Export citation
A Multi-Frey Approach to Some Multi-Parameter Families of Diophantine Equations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 491-519
-
- Article
-
- You have access
- Export citation
Matrices Whose Norms Are Determined by Their Actions on Decreasing Sequences
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 520-531
-
- Article
-
- You have access
- Export citation
Local Bounds for Torsion Points on Abelian Varieties
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 532-555
-
- Article
-
- You have access
- Export citation
Polarization of Separating Invariants
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 556-571
-
- Article
-
- You have access
- Export citation
Non-Selfadjoint Perturbations of Selfadjoint Operators in Two Dimensions IIIa. One Branching Point
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 572-657
-
- Article
-
- You have access
- Export citation
Inverse Pressure Estimates and the Independence of Stable Dimension for Non-Invertible Maps
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 658-684
-
- Article
-
- You have access
- Export citation
Closed and Exact Functions in the Context of Ginzburg–Landau Models
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 685-702
-
- Article
-
- You have access
- Export citation
Award Winners
Research Article
𝓏-Stable ASH Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 703-720
-
- Article
-
- You have access
- Export citation