Hostname: page-component-8448b6f56d-mp689 Total loading time: 0 Render date: 2024-04-19T17:28:29.767Z Has data issue: false hasContentIssue false
  • English
  • Français

𝓏-Stable ASH Algebras

Published online by Cambridge University Press:  20 November 2018

Andrew S. Toms  and
Wilhelm Winter
Andrew S. Toms
Affiliation:
Department of Mathematics and Statistics, University of New Brunswick, Fredericton, NB, E3B 5A3 e-mail:, atoms@math.unb.ca
Wilhelm Winter
Affiliation:
Mathematisches Institut der Universität Münster, Einsteinstr. 62, D-48149 Münster, Germany e-mail:, wwinter@math.uni-muenster.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

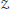The Jiang–Su algebra $Z$ has come to prominence in the classification program for nuclear 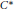${{C}^{*}}$-algebras of late, due primarily to the fact that Elliott’s classification conjecture in its strongest form predicts that all simple, separable, and nuclear 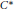${{C}^{*}}$-algebras with unperforated $\text{K}$-theory will absorb 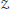$Z$ tensorially, i.e., will be 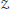$Z$-stable. There exist counterexamples which suggest that the conjecture will only hold for simple, nuclear, separable and 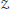$Z$-stable 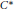${{C}^{*}}$-algebras. We prove that virtually all classes of nuclear 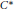${{C}^{*}}$-algebras for which the Elliott conjecture has been confirmed so far consist of 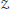$Z$-stable 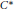${{C}^{*}}$-algebras. This follows in large part from the following result, also proved herein: separable and approximately divisible 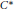${{C}^{*}}$-algebras are 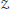$Z$-stable.

Keywords

46L8546L35nuclear C*-algebrasK-theoryclassification
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 60 , Issue 3 , 01 June 2008 , pp. 703 - 720
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Brown, N., Invariant means and finite representation theory of C*-algebras. Mem. Amer.Math. Soc. 184(2006), no. 865.Google Scholar
[2] Dadarlat, M. and Gong, G., A classification result for approximately homogeneous C*-algebras of real rank zero. Geom. Funct. Anal. 7(1997), no. 4, 646–711.Google Scholar
[3] Elliott, G. A., The classification problem for amenable C*-algebras. Proceedings of the International Congress of Mathematicians, Birkhäuser, Basel, 1995, pp. 922–932.Google Scholar
[4] Elliott, G. A., A classification of certain simple C*-algebras. In: Quantum and Noncommutative Analysis. Math. Phys. Stud. 16, Kluwer Academic Publications, Dordrecht, 1993, pp. 373–385.Google Scholar
[5] Elliott, G. A., Gong, G., and Li, L., On the classification of simple inductive limit C*-algebras. II: The isomorphism theorem. Invent.Math. 168(2007), no. 2, 249–320.Google Scholar
[6] Elliott, G. A., Gong, G., and Li, L., Approximate divisibility of simple inductive limit C*-algebras. Contemp.Math. 228(1998), 87–97.Google Scholar
[7] Elliott, G. A., Gong, G., Jiang, X., and Su, H., A classification of simple limits of dimension drop C*-algebras. In: Operator Algebras and Their Applications, Fields Inst. Commun. 13, American Mathematical Society, Providence, RI, 1997, pp. 125–144.Google Scholar
[8] Gong, G., Jiang, X., and Su, H., Obstructions to Z-stability for unital simple C*-algebras. Canad. Math. Bull. 43(2000), no. 4, 418–426.Google Scholar
[9] Husemoller, D., Fibre Bundles. McGraw-Hill, New York, 1966.Google Scholar
[10] Ivanescu, C., On the classification of simple approximately subhomogeneous C*-algebras not necessarily of real rank zero, arXiv: math.OA/0312044.Google Scholar
[11] Jiang, X., Nonstable K-theory for Z-stable C*-algebras. arXiv: math.OA/9707228.Google Scholar
[12] Jiang, X. and Su, H., On a simple unital projectionless C*-algebra. Amer. J. Math. 121(1999), no. 2, 359–413.Google Scholar
[13] Jiang, X. and Su, H., A classification of simple limits of splitting interval algebras, J. Funct. Anal. 151(1997), no. 1, 50–76.Google Scholar
[14] Kirchberg, E., The classification of purely infinite C*-algebras using Kasparov's theory. Fields Inst. Commun., to appear.Google Scholar
[15] Kirchberg, E. andW.Winter, Covering dimension and quasidiagonality. Internat. J. Math. 15(2004), no. 1, 63–85.Google Scholar
[16] Lin, H., Classification of simple tracially AF C*-algebras. Canad. J. Math. 53(2001), no. 1, 161–194.Google Scholar
[17] Mygind, J., Classification of certain simple C*-algebras with torsion in K1 . Canad. J. Math. 53(2001), no. 6, 1223–1308.Google Scholar
[18] Ng, P.W., Simple real rank zero algebras with locally Hausdorff spectrum. Proc. Amer.Math. Soc. 134(2006), no. 8, 2223–2228.Google Scholar
[19] Perera, F. and Rørdam, M., AF-embeddings into C*-algebras with real rank zero. J. Funct. Anal. 217(2004), no. 1, 142–170.Google Scholar
[20] Razak, S., On the classification of simple stably projectionless C*-algebras. Canad. J.Math. 54(2002), no. 1, 138–224.Google Scholar
[21] Rørdam, M., Classification of Nuclear C*-Algebras. Encyclopaedia of Mathematical Sciences 126, Springer-Verlag, Berlin, 2002.Google Scholar
[22] Rørdam, M. A simple C*-algebra with a finite and an infinite projection. Acta Math. 191 (2003), no. 1, 109–142.Google Scholar
[23] Rørdam, M., The stable and the real rank of Z-absorbing C*-algebras. arXiv: math.OA/0408020.Google Scholar
[24] Rørdam, M., Larsen, F., and Laustsen, N., An Introduction to K-Theory for C*-Algebras, London Mathematical Society Student Texts 49, Cambridge University Press, Cambridge, 2000.Google Scholar
[25] Stevens, I., Simple approximate circle algebras. In: Operator Algebras and Their Applications. II. Fields Inst. Commun. 20, American Mathematical Society, Providence, RI, 1998, pp. 97–104.Google Scholar
[26] Stevens, K., The classification of certain non-simple approximate interval algebras. In: Operator Algebras and Their Applications. II. Fields Inst. Commun. 20, American Mathematical Society, Providence, RI, 1998, pp. 105–148.Google Scholar
[27] Thomsen, K., Limits of certain subhomogeneous C*-algebras. Mém. Soc. Math. Fr. 1997, no. 71.Google Scholar
[28] Toms, A. S., On the independence of K-theory and stable rank for simple C*-algebras. J. Reine Angew.Math. 578(2005), 185–199.Google Scholar
[29] Toms, A. S., On the classification problem for nuclear C*-algebras, Ann. of Math. (2), to appear.Google Scholar
[30] Toms, A. S. andW.Winter, Strongly self-absorbing C*-algebras. Trans. Amer. Math. Soc. 359(2007), no. 8, 3999–4029 (electronic).Google Scholar
[31] Tsang, K., A classification of certain simple stably projectionless C*-algebras, preprint (2004).Google Scholar
[32] Villadsen, J., On the stable rank of simple C*-algebras. J. Amer.Math. Soc. 12(1999), 1091–1102.Google Scholar
[33] Villadsen, J., The range of the Elliott invariant of the simple AH algebras with slow dimension growth. K-Ttheory 15(1998), no. 1, 1–12.Google Scholar
[34] Winter, W., On topologically finite-dimensional simple C*-algebras. arXiv: math.OA/0311501.Google Scholar
[35] Winter, W., On the classification of simple Z-stable C*-algebras with real rank zero and finite decomposition rank. J. LondonMath. Soc. 74(2006), no. 1, 167–183.Google Scholar
[36] Winter, W. Simple C*-algebras with locally finite decomposition rank, J. Funct. Anal. 243(2007), no. 2, 394–425.Google Scholar