Hostname: page-component-848d4c4894-8kt4b Total loading time: 0 Render date: 2024-06-27T07:20:01.105Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Growth of Blaschke Products

Published online by Cambridge University Press:  20 November 2018

G. R. MacLane  and
L. A. Rubel
G. R. MacLane
Affiliation:
Purdue University, Lafayette, Indiana University of Illinois, Urbana, Illinois
L. A. Rubel
Affiliation:
Institute for Advanced Study, Princeton, New Jersey
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is well known that the distribution of the zeros of an analytic function affects its rate of growth. The literature is too extensive to indicate here. We only point out (1, p. 27; 2; 3; 5), where the angular distribution of the zeros plays a role, as it will in this paper. In private communication, A. Zygmund has raised the following related question, which is the subject of our investigation here.

Let {zn}, n = 1, 2, 3, …, be a sequence of non-zero complex numbers of modulus less than 1, such that ∑(1 – |zn|) < ∞, and consider the Blaschke product

1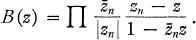

Let

2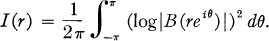

What are the sequences {zn} for which I(r) is a bounded function of r?

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 595 - 601
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Boas, R. P., Entire functions (Academic Press, New York, 1954).Google Scholar
2. Linden, C. N., The distribution of the zeros of regular functions, Proc. London Math. Soc. (3) 15 (1965), 301–322.Google Scholar
3. Linden, C. N., The representation of regular functions, J. London Math. Soc. 39 (1964), 19–30.Google Scholar
4. Rubel, L. A., A Fourier series method for entire functions, Duke Math. J. 30 (1963), 437–442.Google Scholar
5. Rubel, L. A. and Taylor, B. A., A Fourier series method for meromorphic and entire functions, Bull. Soc. Math. France 96 (1968), 53–96.Google Scholar