In this paper, it is shown that the theory of perturbed generalised Hamiltonian systems provides an effective method for understanding the description of flow patterns of some three-dimensional flows. Firstly, theorems for the persistence of periodic solutions of three-dimensional generalised Hamiltonian systems under perturbation are given by developing Melnikov's method. Then, three different systems of three-dimensional steady fluid flows are discussed and the existence or non-existence of periodic solutions of these systems is proved.

In this work, we generalise the study of Favard's Problems to the weighted diameters of a complete set of conjugate algebraic integers, that is, the roots of an irreducible monic polynomial with coefficients in ℤ.

Difference equations with piecewise continuous nonlinearities and their singular perturbations, first order neutral type delay differential equations with small parameters, are considered. Solutions of the difference equations are shown to be asymptotically periodic with period-adding bifurcations and bifurcations determined by Farey's rule taking place for periods and types of solutions. Solutions of the singularly perturbed delay differential equations are considered and compared with solutions of the difference equations within finite time intervals. The comparison is based on a continuous dependence of solutions on the singular parameter.

If a Banach space X contains a complemented subspace isomorphic to c0 (respectively, ℓ1), then X contains complemented almost isometric copies of c0 (respectively, ℓ1). If a Banach space X is such that X* contains a subspace isomorphic to L1[0, 1] (respectively, ℓ∞), then X* contains almost isometric copies of L1[0, 1] (respectively, ℓ∞).

Banach's original proof of the Banach-Stone theorem for compact metric spaces uses peak functions, that is, continuous functions which assume their norm in just one point. We show by using nonstandard methods that the peak point approach also works for compact Hausdorff spaces. The peak functions are replaced by internal functions whose standard part is supported in one monad.

In this paper we consider the characterisation of those elements of a transformation semigroup S which are a product of two proper idempotents. We give a characterisation where S is the endomorphism monoid of a strong independence algebra A, and apply this to the cases where A is an arbitrary set and where A is an arbitrary vector space. The results emphasise the analogy between the idempotent generated subsemigroups of the full transformation semigroup of a set and of the semigroup of linear transformations from a vector space to itself.

A compact quantum group is defined to be a unital Hopf C*–algebra generated by the matrix elements of a family of invertible corepresentations. We present a version of the Tannaka–Krein duality theorem for compact quantum groups in the context of abstract categories; this result encompasses the result of Woronowicz and the classical Tannaka-Krein duality theorem. We construct the orthogonality relations (similar to the case of compact groups). The Plancherel theorem is then established.

A Banach space X is said to have uniform property (K) if there exists a constant (k ∈ [0,1) such that whenever xn ⇀ 0, ∥xn∥ → 1, and we have lim sup ∥ym∥ ≤ k. This property is the uniform version of property (K) recently introduced by B. Sims (Bull. Austral. Math. Soc. 50(1994), 523–528). Sufficient conditions for uniform property (K) are given. Some examples are presented to separate various Banach space properties. Applications to nonlinear operators are also included.

We prove that semi-symmetric ball-homogeneous spaces are locally symmetric and we use this result to prove that a semi-symmetric Riemannian manifold such that the volume of each sufficiently small geodesic ball is the same as in a Euclidean space, is locally flat.

Let C be a nonempty closed convex subset of a real Banach space E and let S, T be nonexpansive mappings of C into itself. In this paper, we consider the following iteration procedure of Mann's type for approximating common fixed points of two mappings S and T:

where {αn is a sequence in [0,1]. Using some ideas in the nonlinear ergodic theory, we prove that the iterates converge weakly to a common fixed point of the nonexpansive mappings T and S in a uniformly convex Banach space which satisfies Opial's condition or whose norm is Fréchet differentiable.

We find presentations for the groups of Cappell-Shaneson 2-knots and other solvable 2-knot groups which are optimal in terms of deficiency and number of generators.

We introduce and study two semigroups of operators u+ and u_, defined in terms of unconditionally converging series. We prove a lifting result for unconditionally converging series that allows us to show examples of operators in u+. We obtain perturbative characterisations for these semigroups and, as a consequence, we derive characterisations for some classes of Banach spaces in terms of the semigroups. If u+(X, Y) is non-empty and every copy of c0 in Y is complemented, then the same is true in X. We solve the perturbation class problem for the semigroup u_, and we show that a Banach space X contains no copies of ℓ∞ if and only if for every equivalent norm |·| on X, the semiembeddings of (X, |·|) belong to u+.

A variety of topological groups is a class of (not necessarily Hausdorff) topological groups closed under the operations of forming subgroups, quotient groups and arbitrary products. It is well known that the class of groups underlying the topological groups contained in any variety of topological groups is a variety of groups. Much work on topological groups is restricted to Hausdorff topological groups and so it is relevant to know if the class of groups underlying Hausdorff topological groups in is a variety of groups. It is shown that this is not always the case. Indeed it is proved that this is not the case for an important proper class of varieties of topological groups.

Motivated by a question related to the construction of the Baum-Connes analytical assembly map for locally compact groups, we refine a criterion of Godement for amenability: for a unimodular group G, our criterion says that G is amenable if and only if every compactly supported, positive-definite function has non-negative integral over G.

This paper extends some fundamental concepts of qualitative matrix analysis from sign pattern classes of real matrices to sign pattern classes of complex matrices. A complex sign pattern and its corresponding sign pattern class are defined in such a way that they generalize the definitions of a (real) sign pattern and its corresponding sign pattern class. A survey of several qualitative results on complex sign patterns is presented. In particular, sign nonsingular complex patterns are investigated. The type of region in the complex plane representing the distribution of the determinants of the matrices in the sign pattern class of a sign nonsingular complex pattern is identified. Cyclically nonnegative complex patterns and complex patterns that are signature similar to nonnegative patterns are characterized. Extensions of sign stable and sign semistable patterns from the real to the complex case are given. Results on ray patterns are also obtained. Finally, many open questions are mentioned.

Let p be a complex polynomial, of the form 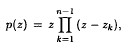, where |zk| ≥ 1 when 1 ≤ k ≤ n − 1. Then p′(z) ≠ 0 if |z| /n.

Let B(z, r) denote the open ball in 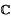with centre z and radius r, and 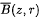denote its closure. The Gauss-Lucas theorem states that every critical point of a complex polynomial p of degree at least 2 lies in the convex hull of its zeros. This theorem has been further investigated and developed. B. Sendov conjectured that, if all the zeros of p lie in 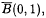then, for any zero ζ of p, the disc 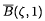contains at least one zero of p′; see [3, Problem 4.1]. This conjecture has attracted much attention-see, for example, [1], and the papers cited there. In connection with this conjecture, Brown [2] posed the following problem.