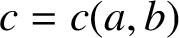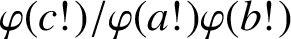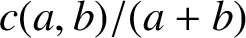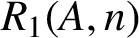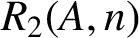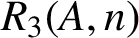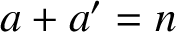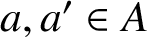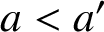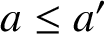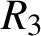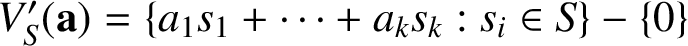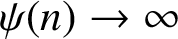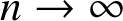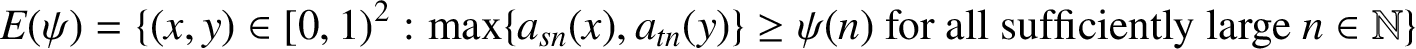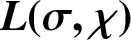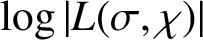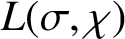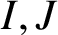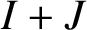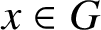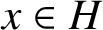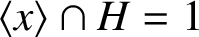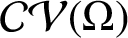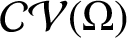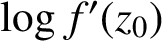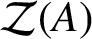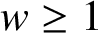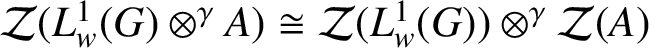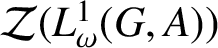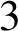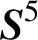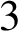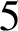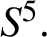Research Article
ON QUOTIENTS OF VALUES OF EULER’S FUNCTION ON FACTORIALS
- Part of:
-
- Published online by Cambridge University Press:
- 17 November 2021, pp. 353-364
-
- Article
- Export citation
ON A PROBLEM ABOUT ADDITIVE REPRESENTATION FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 08 February 2022, pp. 365-371
-
- Article
- Export citation
TIGHT UNIVERSAL TRIANGULAR FORMS
- Part of:
-
- Published online by Cambridge University Press:
- 18 November 2021, pp. 372-384
-
- Article
- Export citation
ON THE MODULARITY OF SOLUTIONS TO CERTAIN DIFFERENTIAL EQUATIONS OF HYPERGEOMETRIC TYPE
- Part of:
-
- Published online by Cambridge University Press:
- 15 September 2021, pp. 385-391
-
- Article
- Export citation
ON TRANSCENDENTAL CONTINUED FRACTIONS IN FIELDS OF FORMAL POWER SERIES OVER FINITE FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 01 October 2021, pp. 392-403
-
- Article
- Export citation
ON THE INCREASING PARTIAL QUOTIENTS OF CONTINUED FRACTIONS OF POINTS IN THE PLANE
- Part of:
-
- Published online by Cambridge University Press:
- 17 December 2021, pp. 404-411
-
- Article
- Export citation
A NOTE ON LARGE VALUES OF
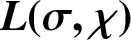 $\boldsymbol{L(\sigma ,\chi )}$
$\boldsymbol{L(\sigma ,\chi )}$
- Part of:
-
- Published online by Cambridge University Press:
- 04 October 2021, pp. 412-418
-
- Article
- Export citation
ON FINE SELMER GROUPS AND SIGNED SELMER GROUPS OF ELLIPTIC MODULAR FORMS
- Part of:
-
- Published online by Cambridge University Press:
- 19 April 2022, pp. 419-430
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE STRONG METRIC DIMENSION OF A TOTAL GRAPH OF NONZERO ANNIHILATING IDEALS
- Part of:
-
- Published online by Cambridge University Press:
- 04 November 2021, pp. 431-439
-
- Article
- Export citation
MONOMIAL AND MONOLITHIC CHARACTERS OF FINITE SOLVABLE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 05 October 2021, pp. 440-448
-
- Article
- Export citation
ISOLATED SUBGROUPS OF FINITE p-GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 01 October 2021, pp. 449-457
-
- Article
- Export citation
SECOND HANKEL DETERMINANT OF LOGARITHMIC COEFFICIENTS OF CONVEX AND STARLIKE FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 30 September 2021, pp. 458-467
-
- Article
- Export citation
AN APPLICATION OF SCHUR’S ALGORITHM TO VARIABILITY REGIONS OF CERTAIN ANALYTIC FUNCTIONS II
- Part of:
-
- Published online by Cambridge University Press:
- 02 December 2021, pp. 468-481
-
- Article
- Export citation
ON THE BOUNDARY BEHAVIOUR OF FRIDMAN INVARIANTS
- Part of:
-
- Published online by Cambridge University Press:
- 22 September 2021, pp. 482-489
-
- Article
- Export citation
CENTRE OF BANACH ALGEBRA VALUED BEURLING ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 13 September 2021, pp. 490-498
-
- Article
- Export citation
A NOTE ON OPEN BOOK EMBEDDINGS OF
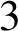 $3$
-MANIFOLDS IN
$3$
-MANIFOLDS IN
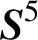 $\boldsymbol {S}^5$
$\boldsymbol {S}^5$
- Part of:
-
- Published online by Cambridge University Press:
- 04 October 2021, pp. 499-506
-
- Article
- Export citation
Abstracts of Australasian PhD Theses
INTERSECTION OF CONJUGATE SOLVABLE SUBGROUPS IN FINITE CLASSICAL GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 14 March 2022, pp. 507-510
-
- Article
-
- You have access
- HTML
- Export citation
MODEL-BASED ADAPTIVE MONITORING: IMPROVING THE EFFECTIVENESS OF REEF MONITORING PROGRAMS
- Part of:
-
- Published online by Cambridge University Press:
- 09 February 2022, pp. 511-513
-
- Article
-
- You have access
- HTML
- Export citation
ADVERSARIAL RISK ANALYSIS FOR FIRST-PRICE SEALED-BID AUCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 08 February 2022, pp. 514-515
-
- Article
-
- You have access
- HTML
- Export citation
CONFIDENCE INTERVALS IN GENERAL REGRESSION MODELS THAT UTILISE UNCERTAIN PRIOR INFORMATION
- Part of:
-
- Published online by Cambridge University Press:
- 08 February 2022, pp. 516-517
-
- Article
-
- You have access
- HTML
- Export citation