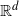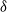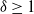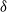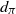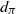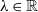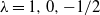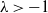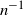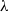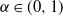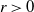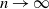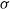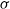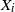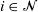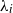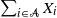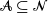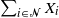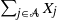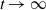217 results in 62Exx
A remark on exact simulation of tempered stable Ornstein–Uhlenbeck processes
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 02 May 2024, pp. 1-3
-
- Article
-
- You have access
- HTML
- Export citation
ON THE CUMULATIVE DISTRIBUTION FUNCTION OF THE VARIANCE-GAMMA DISTRIBUTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 29 January 2024, pp. 1-9
-
- Article
- Export citation
Normal approximation in total variation for statistics in geometric probability
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 03 July 2023, pp. 106-155
- Print publication:
- March 2024
-
- Article
- Export citation
Distribution and moments of the error term in the lattice point counting problem for three-dimensional Cygan–Korányi balls
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 19 May 2023, pp. 830-861
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Distributions of random variables involved in discrete censored δ-shock models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 19 May 2023, pp. 1144-1170
- Print publication:
- December 2023
-
- Article
- Export citation
On Bayesian credibility mean for finite mixture distributions
- Part of
-
- Journal:
- Annals of Actuarial Science / Volume 18 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 29 March 2023, pp. 5-29
-
- Article
- Export citation
Exactly solvable urn models under random replacement schemes and their applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 14 February 2023, pp. 835-854
- Print publication:
- September 2023
-
- Article
- Export citation
A negative binomial approximation in group testing
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 4 / October 2023
- Published online by Cambridge University Press:
- 28 October 2022, pp. 973-996
-
- Article
- Export citation
Multivariate Poisson and Poisson process approximations with applications to Bernoulli sums and
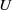 $U$
-statistics
$U$
-statistics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 30 September 2022, pp. 223-240
- Print publication:
- March 2023
-
- Article
- Export citation
Bounds for the chi-square approximation of the power divergence family of statistics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 09 August 2022, pp. 1059-1080
- Print publication:
- December 2022
-
- Article
- Export citation
Community detection and percolation of information in a geometric setting
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 31 May 2022, pp. 1048-1069
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ELECTRICAL IMPEDANCE TOMOGRAPHY USING NONCONFORMING MESH AND POSTERIOR APPROXIMATED REGRESSION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 03 March 2022, pp. 520-522
- Print publication:
- June 2022
-
- Article
-
- You have access
- HTML
- Export citation
On reconsidering entropies and divergences and their cumulative counterparts: Csiszár's, DPD's and Fisher's type cumulative and survival measures
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 21 February 2022, pp. 294-321
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
How a probabilistic analogue of the mean value theorem yields stein-type covariance identities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 18 January 2022, pp. 350-365
- Print publication:
- June 2022
-
- Article
- Export citation
A generalised Dickman distribution and the number of species in a negative binomial process model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 01 July 2021, pp. 370-399
- Print publication:
- June 2021
-
- Article
- Export citation
Exact simulation of Ornstein–Uhlenbeck tempered stable processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 23 June 2021, pp. 347-371
- Print publication:
- June 2021
-
- Article
- Export citation
Normal approximation for mixtures of normal distributions and the evolution of phenotypic traits
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 17 March 2021, pp. 162-188
- Print publication:
- March 2021
-
- Article
- Export citation
Asymptotic normality in t-stack sortable permutations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 04 November 2020, pp. 1062-1070
-
- Article
- Export citation
Explicit results on conditional distributions of generalized exponential mixtures
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 760-774
- Print publication:
- September 2020
-
- Article
- Export citation
Explicit asymptotics on first passage times of diffusion processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 15 July 2020, pp. 681-704
- Print publication:
- June 2020
-
- Article
- Export citation