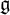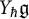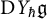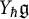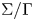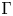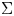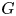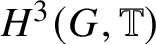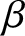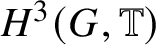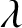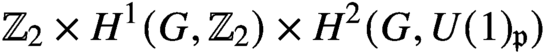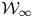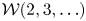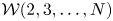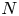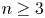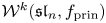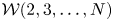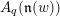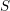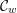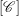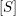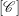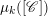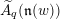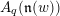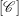44 results in 81Rxx
On the structure of some one-generator braces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 20 March 2024, pp. 566-576
-
- Article
- Export citation
The restricted quantum double of the Yangian
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 16 February 2024, pp. 1-72
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Spectral Gap and Low-Energy Spectrum in Mean-Field Quantum Spin Systems
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 06 December 2023, e112
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equivariant
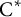 $\textrm {C}^*$-correspondences and compact quantum group actions on Pimsner algebras
$\textrm {C}^*$-correspondences and compact quantum group actions on Pimsner algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 05 December 2023, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Conformal blocks for Galois covers of algebraic curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 29 August 2023, pp. 2191-2259
- Print publication:
- October 2023
-
- Article
- Export citation
Comparison of quantizations of symmetric spaces: cyclotomic Knizhnik–Zamolodchikov equations and Letzter–Kolb coideals
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 02 May 2023, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Jordan–Hölder theorem for skew left braces and their applications to multipermutation solutions of the Yang–Baxter equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 24 April 2023, pp. 793-809
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the primality of totally ordered q-factorization graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 20 March 2023, pp. 594-637
- Print publication:
- April 2024
-
- Article
- Export citation
ACTIONS OF MONOIDAL CATEGORIES AND REPRESENTATIONS OF CARTAN TYPE LIE ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 22 February 2022, pp. 2367-2402
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An
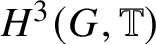 $H^{3}(G,{\mathbb T})$-valued index of symmetry-protected topological phases with on-site finite group symmetry for two-dimensional quantum spin systems
$H^{3}(G,{\mathbb T})$-valued index of symmetry-protected topological phases with on-site finite group symmetry for two-dimensional quantum spin systems
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 16 December 2021, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Inverse K-Chevalley formulas for semi-infinite flag manifolds, I: minuscule weights in ADE type
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 07 July 2021, e51
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniconnected solutions to the Yang–Baxter equation arising from self-maps of groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 20 April 2021, pp. 225-233
- Print publication:
- March 2022
-
- Article
- Export citation
The classification of symmetry protected topological phases of one-dimensional fermion systems
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 16 March 2021, e25
-
- Article
-
- You have access
- Open access
- Export citation
Universal two-parameter 𝒲∞-algebra and vertex algebras of type 𝒲(2, 3, …, N)
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 10 February 2021, pp. 12-82
- Print publication:
- January 2021
-
- Article
- Export citation
One-generator braces and indecomposable set-theoretic solutions to the Yang–Baxter equation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 06 May 2020, pp. 676-696
-
- Article
- Export citation
Quantum Langlands duality of representations of
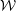 ${\mathcal{W}}$-algebras
${\mathcal{W}}$-algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 12 / December 2019
- Published online by Cambridge University Press:
- 04 October 2019, pp. 2235-2262
- Print publication:
- December 2019
-
- Article
- Export citation
Laurent phenomenon and simple modules of quiver Hecke algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 12 / December 2019
- Published online by Cambridge University Press:
- 04 October 2019, pp. 2263-2295
- Print publication:
- December 2019
-
- Article
- Export citation
QUANTUM INCREASING SEQUENCES GENERATE QUANTUM PERMUTATION GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 27 September 2019, pp. 631-639
- Print publication:
- September 2020
-
- Article
- Export citation
CONVEXITY OF PARAMETER EXTENSIONS OF SOME RELATIVE OPERATOR ENTROPIES WITH A PERSPECTIVE APPROACH
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 06 June 2019, pp. 737-744
- Print publication:
- September 2020
-
- Article
- Export citation
Rigid C*-Tensor Categories and their Realizations as Hilbert C*-Bimodules
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 16 November 2018, pp. 367-393
-
- Article
- Export citation